
Aniq integrallar
.pdf
Jeterliligi. Meyli f (x) funkciyası [a,b] segmentinde shegaralanǵan hám
|
lim (ST sT ) 0 teńligi orınlı bolsın. Darbu qosındılarınıń 5-qasiyetinen |
|
|||||||||||||||||||||||||||||||||||||||||||||
(T ) 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 I I |
|
|
|
|
|
|
|
|
|
lim (ST sT ) 0 |
|
|
|
|
||||||||||||||||
|
s |
I |
|
I * S |
. |
|
|
Onda |
S |
s |
|
hám |
|
|
|
|
|
sheginiń |
|||||||||||||||||||||||||||||
|
T |
* |
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
T |
|
|
|
(T ) 0 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
anıqlamasınan |
|
|
0 ( ) 0: |
(T ) |
T , |
|
|
|
0 ST |
sT |
|||||||||||||||||||||||||||||||||||||
bolǵanı ushın |
0 I |
I S |
s |
|
|
teńsizligi |
[a,b] |
|
|
|
segmentiniń |
|
(T ) |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bolǵan T |
maydalawında orınlı boladı. Onda I hám I sanları T maydalawınan |
||||||||||||||||||||||||||||||||||||||||||||||
ǵárezli |
emesligi, |
0 sanınıń |
erikli |
ekenliginen |
|
I |
|
|
|
|
iye bolamız. Endi |
||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
||
|
I I |
|
J |
|
belgilewin kiritip, |
s |
T |
I |
I * S |
teńsizligi tiykarında |
|
s |
T |
J S |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
|
T |
sT T ( ) ST |
|
|
|
|
|
|
T |
|||||||||||||
hám Darbu |
qosındılarınıń |
|
1-qasiyetinde |
|
bolganı |
|
ushın, |
||||||||||||||||||||||||||||||||||||||||
|
T ( ) J |
|
ST sT |
teńsizligine iye bolamiz. Bul |
|
|
f (x) funkciyası |
[a,b] |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
segmentinde integrallanıwshı |
hám |
onıń integrali |
|
J |
|
|
ge |
teń bolıwın |
|
|
ańlatadı. |
||||||||||||||||||||||||||||||||||||
Teorema dálillendi. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
Dálillengen |
teoremadan |
eger |
|
f (x) |
|
funkciyası |
|
|
[a,b] |
|
|
segmentinde |
||||||||||||||||||||||||||||||||
integrallanıwshı hám onıń integralı |
J |
sanına teń bolsa, onda |
J inf ST |
sup sT |
|||||||||||||||||||||||||||||||||||||||||||
teńligi orınlı bolıwın kóremiz. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Eskertiw. ST sT (Mk mk ) xk k ( f ) xk |
|
teńligin |
esapqa |
alsaq, |
onda |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) |
|
funkciyasınıń |
[a,b] |
segmentinde integrallanıwshı bolıw ushın orınlı hám |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
jeterli shartti, ST sT k ( f ) xk 0, eger (T ) 0 , túrinde jazıw múmkin. |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3-§. Integrallanıwshı funkciyalar klassları |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
1-teorema. Eger |
f (x) funkciyası |
[a,b] |
segmentinde úzliksiz bolsa, onda ol |
||||||||||||||||||||||||||||||||||||||||||
usı segmentte integrallanıwshı funkciya boladı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
Dálilleniwi. Meyli |
|
f (x) |
funkciyası [a,b] |
segmentinde úzliksiz bolsın. |
|
||||||||||||||||||||||||||||||||||||||||
Onda Kantor teoremasına sáykes |
|
f (x) |
funkciyası [a,b] |
|
|
segmentinde teń |
|
||||||||||||||||||||||||||||||||||||||||
|
ólshewli úzliksiz, yaǵnıy |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|||||||||||||||||||||||||||
|
|
( ) 0 : x , x |
[a,b]: x |
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
f (x |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
. |
|
Endi |
|
[a,b] |
|
segmentiniń |
|
|
maydalanıwı |
|||||||||||||||||||||||||||||
|
f (x ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
(T ) max x |
|
|
|
bolǵan |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
maydalawındaǵı |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
0,n} |
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
k 1,n |
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
{xk , k |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
xk |
xk xk 1 , dara |
|
|
|
||||||||||||||||||||||||||||||||||||||||
k [xk 1, xk ], k 1,n |
, |
segmentleriniń hárbirinde |
|
f (x) |
|||||||||||||||||||||||||||||||||||||||||||
funkciyası |
|
|
úzliksiz |
bolǵanı |
|
|
ushın |
Veyershtrass |
teoremasına |
|
sáykes |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f ( k ) mk inf |
|
||||||||||||||||||||||||||
k , k k , k 1, n |
|
|
|
|
|
|
noqatları |
|
bar |
boladı |
|
|
da |
|
|
f (x), |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x k |
|
|

f ( ) M |
sup f (x) , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xk xk 1 |
|
(T ) . |
||||||||||||||
k 1, n |
boladı. Bunda |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
k |
k |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
x k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Teń |
ólshewli |
úzliksizlik |
|
|
anıqlaması |
|
tiykarında |
|
|
k ( f ) Mk |
mk |
|||||||||||||||||||||||||||||||
f ( ) f ( ) |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1,n |
|
|
|
|
|
teńsizligin |
|
jazıw |
|
|
múmkin. |
Bunnan |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
b a |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
S s ( f )x |
|
|
|
|
|
|
x |
bolıwın kóremiz. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
T |
T |
k |
|
|
k |
|
|
b a k 1 |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Demek, |
f (x) |
|
funkciyası |
|
|
|
ST sT |
k ( f ) xk 0, eger (T ) 0 |
shártin |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
qanaatlandıradı, |
al bul |
|
|
|
f (x) |
|
|
funkciyası |
|
[a,b] |
|
segmentinde |
integrallanıwshı |
|||||||||||||||||||||||||||||
bolıwı ushın zárúrli hám jeterli. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2-teorema. Eger |
|
f (x) |
|
funkciyası |
|
[a,b] |
segmentinde |
anıqlanǵan hám |
||||||||||||||||||||||||||||||||||
monoton funkciya bolsa, onda ol |
[a,b] |
|
|
segmentinde integrallanıwshı funkciya |
||||||||||||||||||||||||||||||||||||||
boladı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dálilleniwi. Meyli |
f (x) funkciyası |
[a,b] segmentinde kemeyiwshi funkciya |
||||||||||||||||||||||||||||||||||||||||
bolsın, onda x [a,b] |
ushın |
f (b) f (x) f (a) |
teńsizligi orınlanadı. Bul |
|||||||||||||||||||||||||||||||||||||||
f (x) |
funkciyası [a,b] |
segmentinde shegaralanǵan funkciya bolıwın ańlatadı. |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
Endi [a,b] |
segmentiniń T {xk , k 0,n} maydalawın qarastıramız. Onda |
|||||||||||||||||||||||||||||||||||||||||
|
mk f (xk ) inf |
f (x) , Mk |
f (xk 1 ) sup f (x) , |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
k 1, n |
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x k |
|
|
|
|
|
|
|
|
|
|
|
|
x k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
teńlikleri |
orınlı |
boladı, |
|
|
sebebi |
x k |
[xk 1, xk ], k 1,n |
ushın |
||||||||||||||||||||||||||||||||||
f (x |
) f (x) f (xk |
|
1) . |
|
|
|
|
Bunnan |
|
|
|
|
f (xk 1) f (xk ) 0 |
|
hám |
|||||||||||||||||||||||||||
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x (T ) max x |
|
|
|
|
teńsizlikleri |
tiykarında |
|
|
|
S s |
T |
|
||||||||||||||||||||||||||||||
k |
|
|
k 1,n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
n |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(Mk mk ) xk |
( f (xk 1) f (xk )) xk (T ) ( f (xk 1) f (xk )) |
|||||||||||||||||||||||||||||||||||||||||
k 1 |
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
(T )( f (a) f (b)) |
bolıwın kóremiz. Demek, |
ST sT 0 , eger (T ) 0 |
||||||||||||||||||||||||||||||||||||||||
shárti |
orınlı. Bul bolsa |
|
|
f (x) |
|
|
funkciyası [a,b] |
segmentinde integrallanıwshı |
||||||||||||||||||||||||||||||||||
bolıwı ushın zárúrli hám jeterli. Teorema dálillendi. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
3-teorema. Eger |
f (x) |
|
|
|
funkciyası [a,b] |
segmentinde shegaralanǵan hám bólek |
||||||||||||||||||||||||||||||||||||
úzliksiz funkciya bolsa, onda bul funkciya [a,b] |
segmentinde integrallanıwshı. |
|
||||||||||||||||||||||||||||||||||||||||
Dálilleniwi. f (x) funkciyası |
|
|
[a,b] |
segmentinde bólek úzliksiz. Onda ol usı |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
segmentiniń |
shekli |
sandaǵı |
|
ck , k 1, n |
|
noqatlarınan |
basqa |
hárbir noqatında |
||||||||||||||||||||||||||||||||||
úzliksiz. |
a c0 c1 c2 |
|
|
|
cn cn 1 b |
|
dep |
|
|
|
esaplaymız |
|
hám |
|||||||||||||||||||||||||||||

min (c |
c |
|
|
) belgilewin kiritemiz. Onda |
c , k 1,n noqatlarınıń |
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
k |
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
||
k 0,n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
dógerekleri kesilispeydi hám tolıǵı menen [a,b] |
segmentine tiyisli boladı. |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
f (x) |
|
funkciyası |
|
[a,b] |
|
|
|
segmentinde |
shegaralanǵan, |
|
yaǵnıy |
|
|
|
|
|
f (x) |
|
M |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
teńsizligi |
x [a,b] ushın orınlı |
bolatuǵın |
M 0 sanı |
bar. |
|
E1 |
U (ck ) |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
belgilewin |
kiritsek, |
|
onda |
|
|
E [a,b] \ E1 |
|
|
kópligi |
jabıq(tuyıq) |
kóplik |
boladı. |
|||||||||||||||||||||||||||||||||
Bunda |
|
|
min( , |
|
|
|
) |
hám |
E E |
|
|
, E E [a,b]. |
|
Onda |
|
|
f (x) |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
24nM |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
funkciyası |
E kópliginde Kantor teoremasına sáykes teń ólshewli úzliksiz, yaǵnıy |
||||||||||||||||||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
( ) 0 :x , x E : x x |
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
, |
||||||||||||||||||||||||||||
|
|
|
|
|
|
f (x ) f (x |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[a,b] |
|
|
|
|
|
|
|
2(b a) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
shárti |
orınlanǵan. Endi |
|
|
|
|
|
|
belgilewin kiritip, |
|
|
segmentiniń |
||||||||||||||||||||||||||||||||||
min( , ) |
|
|
|||||||||||||||||||||||||||||||||||||||||||
diametri |
(T ) |
|
bolatuǵın |
T {xk , k m} |
|
|
maydalawın |
|
qarastıramız. |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sonda ST sT |
k ( f ) xk k ( f ) xk k ( f ) xk k ( f ) xk |
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
k E |
|
|
|
|
|
|
|
k E1 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
teńligi orınlı boladı. Bul teńliktiń oń |
|
tárepindegi birinshi qosındıǵa T |
|||||||||||||||||||||||||||||||||||||||||||
maydalawınıń tek E kópligine tiyisli |
|
|
kesindiler, ekinshi qosındıǵa T |
||||||||||||||||||||||||||||||||||||||||||
maydalawınıń |
|
tek |
|
E1 |
kópligine |
|
tiyisli |
|
kesindiler, úshinshi qosındıǵa T |
||||||||||||||||||||||||||||||||||||
maydalawınıń E hám E1 kópliklerine kirmegen barlıq kesindiler kiritilgen. |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Birinshi |
qosındıda |
k ( f ) sup |
f (x ) |
f (x |
|
|
|
|
|
|
|
hám |
kesindiler |
qosındısı |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2(b a) |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x,x k E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
b a |
|
dan asıp ketpeydi, ekinshi |
hám úshinshi qosındılarda k ( f ) 2M hám |
||||||||||||||||||||||||||||||||||||||||||
kesindiler |
qosındısı |
|
n 2 dan |
|
asıp |
ketpeydi, |
sebebi úshinshi |
|
qosındıda |
T |
|||||||||||||||||||||||||||||||||||
maydalawınıń intervalları sanı |
2n |
|
nen artıq bola almaydı. Sonıń úshın, |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
m |
|
|
|
|
|
|
(b a) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
S s ( f )x |
|
|
|
|
|
2M 2n 2M 2n |
|
8Mn |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
T |
|
T |
|
|
k |
|
|
k |
|
|
2(b a) |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
24Mn |
|
|
|
|
|
||||||||||
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
5 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
2 |
|
3 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Demek, ST sT k ( f ) xk , eger |
(T ) bolsa. Bul shárttiń orınlı bolıwı |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) |
|
funkciyası |
[a,b] |
|
segmentinde integrallanıwshı bolıwı ushın orınlı hám |
||||||||||||||||||||||||||||||||||||||||
jeterli. Teorema dálillendi. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
4-teorema. |
|
Eger |
f (x) |
|
funkciyası |
|
|
|
[a,b) |
|
|
kesindisinde |
anıqlanan, |
||||||||||||||||||||||||||||||||
shegaralanǵan, |
|
[a,b) |
|
|
ushın |
[a, ] segmentinde integrallanıwshı funkciya |
|||||||||||||||||||||||||||||||||||||||
hám |
lim |
f (x)dx |
shekli shegi bar bolsa, onda f (x) funkciyası [a,b] |
b 0 |
|||
|
|
a |
|
segmentinde integrallanıwshı boladı. Bul teoremanıń dálilin keltirmeymiz.
4-§. Anıq integraldıń qasiyetleri
Eskertiw. 1) f (x) funkciyası [a,b] segmentinde integrallanıwshı bolsa, onda onıń integralı integral astındaǵı ańlatpanıń argumentin qanday harip penen belgilewden ǵárezli bolmaǵan san boladı, yaǵnıy
b b b
f (x)dx f (u)du f (z)dz . |
||
a |
a |
a |
2) Anıq integrallardıń qasiyetleriń Dálilleniwide integral astındaǵı funkciyaısı ushın anıq integraldıń bar bolıwınıń zárúrlı hám jeterli sharti orınlanǵan dep esaplanadı.
1. Funkciyalar ustinde arifmetikalıq ámellerge baylanıslı qasiyetler
1-qasiyet. Eger |
u(x) |
hám v(x) |
funkciyaları |
[a,b] |
segmentinde |
||
integrallanıwshı |
bolsa, onda |
, R |
sanlarında |
f (x) u(x) v(x) |
|||
funkciyası [a,b] |
segmentinde integrallanıwshı boladı hám |
|
|||||
|
b |
|
b |
|
b |
|
|
|
( u(x) v(x))dx u(x)dx v(x)dx |
(1) |
|||||
|
|
||||||
|
a |
|
a |
|
a |
|
|
teńligi orınlı. |
|
|
|
|
|
|
|
Dálilleniwi. [a,b] |
|
|
|
|
|
|
|
segmentiniń tayınlaǵan T maydalawına hám tayınlaǵan |
|||||||
tańlawına dúzilgen u(x) , v(x) hám f (x) funkciyalarınıń integrallıq qosındıların |
|||||||
sáykes T (u, ) , T (v, ) |
hám T ( f , ) arqalı belgilesek, onda |
|
|||||
|
|
T ( f , ) T (u, ) T (v, ) |
(2) |
||||
teńligi orınlı boladı. Eger T maydalawınıń |
(T ) |
maydalılıǵı nolge umtılsa, onda |
|||||
bul teńliginiń oń tárepi shegine iye boladı. Sebebi |
u(x) |
hám v(x) |
funkciyaları |
||||
[a,b] segmentinde integrallanıwshı hám shek sızıqlılıq qasiyetke iye. Onda (2) teńliginiń shep tárepiniń de shegi bar boladı hám bul shekler bir-birine teń bolıwınan (1) formula orınlı boladı.
Dálillengen qasiyet anıq integraldıń sızıqlılıq qasiyeti dep ataladı. Bul sızıqlılıq qasiyetine anıq integraldıń birteklilik hám additivlik qasiyetleri birikken.
2-qasiyet. Eger u(x) hám |
v(x) funkciyaları |
[a,b] |
segmentinde |
integrallanıwshı bolsa, onda |
f (x) u(x) v(x) |
funkciyası |
da [a,b] |
segmentinde integrallanıwshı.

|
|
|
Dálilleniwi. |
|
|
u(x) |
hám |
|
|
v(x) |
|
funkciyaları [a,b] |
|
segmentinde |
||||||||||||||||||||||||||||||||||||||||||
integrallanıwshı |
bolǵanı |
úshın |
|
|
olar |
|
|
|
usı |
segmentte shegaralanǵan, yaǵnıy |
||||||||||||||||||||||||||||||||||||||||||||||
M 0: x [a,b] |
|
u(x) |
|
M , |
|
v(x) |
|
M |
|
|
|
shárti |
|
|
|
orınlı. |
Bunnan |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
f (x) u(x) v(x) |
|
funkciyası |
|
|
da [a,b] |
segmentinde |
|
shegaralanǵan |
|
|
hám |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
[a,b] ushın |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x , x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u(x |
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
f (x |
) f (x ) |
|
u(x )v(x ) u(x |
|
|
)v(x ) |
|
|
)v(x ) u(x |
)v(x |
|
|
|
|
|
|
|
|
|
(3) |
||||||||||||||||||||||||||||||||||
|
|
|
|
u(x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
)) |
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
) |
|
) |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
(u(x ) |
|
))v(x ) u(x |
|
)(v(x ) v(x |
|
M ( u(x ) u(x |
v(x ) v(x |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
teńsizligi orınlı. Endi bul teńsizlikti |
|
[a,b] |
|
|
segmentiniń |
tayınlanǵan |
T |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
maydalawındaı |
[xk 1, xk ], k 1, n |
|
dara |
|
segmentlerinde |
|
jazsaq, onda |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
, |
|
k |
1, n ushın orınlı bolǵan, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
x , x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
sup |
|
|
|
|
|
|
|
|
|
|
|
k ( f ) , |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x ) f (x |
|
|
|
|
|
|
|
f (x ) f (x ) |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x,x k |
|
|
|
|
|
|
|
|
|
|
|
k (u) |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sup |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u(x ) |
|
u(x ) |
|
|
|
|
|
|
|
|
u(x ) |
u(x ) |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x ,x k |
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sup |
|
|
|
|
|
|
(v) |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v(x ) |
|
v(x ) |
|
|
|
|
|
v(x ) |
v(x ) |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x ,x k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
teńsizliklerin esapqa alǵan halda (3) teńsizliginen |
k ( f ) M ( k (u) k (v)) , |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
teńsizlikleri sistemasına iye bolamız. Bul teńsizlikler sistemasınıń |
k |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
k 1, n |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
teńlemesin |
|
xk |
ǵa kóbeytip, payda bolǵan sistemadaǵı |
teńsizliklerdi aǵzama- |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
aǵza |
qossaq, |
k ( f ) xk M ( k (u) xk k (v) xk ) teńsizligi payda |
boladı. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Eger T maydalawınıń (T ) |
|
|
maydalılıǵı nolge umtılsa, onda bul teńsizliginiń oń |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
tárepi nolge umtıladı. Onda shektiń teńsizliklerge baylanıslı qasiyetinen bul
teńsizliginiń |
shep |
tárepiniń |
(T ) 0 daǵı |
shegi nolge |
teń. Bul |
bolsa |
||||
f (x) u(x) v(x) |
funkciyası [a,b] |
segmentinde integrallanıwshı bolıwı ushın |
||||||||
zárúr hám jeterli. |
|
|
|
|
|
|
|
|
|
|
2. Anıq integraldıń integrallaw kesindisine baylanıslı qasiyetleri. |
|
|||||||||
1-qasiyet. Eger |
f (x) |
funkciyası |
[a,b] |
segmentinde integrallanıwshı bolsa, |
||||||
onda ol 1 |
[a1,b1] [a,b] kesindisinde de integrallanıwshı boladı. |
|||||||||
Dálilleniwi. Meyli T |
arqalı |
1 |
|
[a1,b1] |
|
|
|
bolǵan |
||
segmentiniń diametri (T ) |
||||||||||
maydalawı bolsın. [a,b] |
segmentin T usılında sonday maydalaymız, nátiyjede |
|||||||||
T maydalawınıń hárbir |
noqatı |
T |
maydalawına tiyisli hám |
(T ) (T ) |
||||||
teńsizligi orınlı bolsın. |
Bunda |
(T ) , |
T |
maydalawınıń |
diametri. |
Onda |
||||

(T ) 0 (T ) 0 |
hám |
T T , |
k ,T ( f ) xk |
0, k,T ( f ) xk |
0 bolanı |
|||||
ushın k ,T ( f ) xk |
k ,T ( f ) xk |
teńsizligi orınlı boladı. Bunda |
k,T ( f ) , |
|||||||
|
T1 |
|
T |
|
|
|
|
|
|
|
f (x) |
funkciyasınıń |
T maydalawındaǵı |
k dara |
segmentindegi |
terbelisi. |
|||||
(T ) |
0 |
da (T ) 0 |
hám |
f (x) |
funkciyası |
[a,b] |
segmentinde |
|||
integrallanıwshı bolǵanı ushın keyingi teńsizliktiń oń tárepi nolge umtiladı. Sonıń
ushın onıń shep tárepiniń |
(T ) 0 daǵı shegi nolge teń. Bul f (x) funkciyası |
||
[a1,b1 ] segmentinde integrallanıwshı bolıwı ushın hám jeterli. |
|
||
2-qasiyet. Eger f (x) |
funkciyası [a,b] |
segmentinde integrallanıwshı hám |
|
с (a,b) bolsa, onda |
|
|
|
b |
c |
b |
|
f (x)dx f (x)dx f (x)dx |
(4) |
||
|
|||
a |
a |
c |
|
teńligi orınli.
Dálilleniwi. (4)-teńliktiń oń tárepindegi integrallardıń bar bolıwı 1-qasiyetten kelip shıadı. Eger funkciyasınıń segmentiniń T {xk , k 1, n} maydalawındaǵı bazıbir xi c,1 i k bolǵan jadaydaǵı integrallıq qosındısın[a,b] ( f ,T ) , al usı maydalawındaǵı [a,c], [c,b] segmentlerindegi integrallıq
qosındıların sáykes [a,c] ( f ,T ), [c,b] ( f ,T ) |
túrinde belgilesek, onda |
[a,b]( f ,T ) [a,c]( f ,T ) [c,b]( f ,T ) |
|
teńligi orınli. f (x) funkciyası [a,b] |
segmentinde integrallanıwshı bolǵanı |
ushın, bundaǵı harbir integrallıq qosındısı (T ) 0 shegine iye boladı hám (4)- teńligi orınlı.
Dálillengen qasiyettiń |
kerisi |
de |
durıs boladı, yaǵnıy eger с (a,b) |
hám |
|||||
f (x) funkciyası |
[a,c], |
[c,b] |
segmentlerinde integrallanıwshı bolsa, onda ol |
||||||
[a,b] segmentinde integrallanıwshı funkciya boladı. |
|
|
|
|
|||||
3-qasiyet. Eger |
f (x) |
funkciyası |
x a |
noqatında |
anıqlanan bolsa, |
onda |
|||
a |
|
|
|
|
|
|
|
|
|
f (x)dx 0 boladı. |
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
Dálilleniwi. |
f (x)dx |
inegralı |
a b |
jadayında |
harbir |
||||
|
a |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
T ( f , ) f ( k ) xk |
|
|
|
||||||
integrallıq qosındınıńdi xk 0, k 1,n bolǵanı ushın |
|||||||||
k 1 |
|
|
|
|
|
|
|
|
|
nolge teń, yaǵnıy
|
b |
|
|
|
|
|
|
|
|
|
n |
|
|
a |
|
||||||
|
f (x)dx |
|
lim |
T ( f , ) |
lim f ( k ) 0 0 f (x)dx |
|
|||||||||||||||
|
a |
|
|
|
(T ) 0 |
|
|
(T ) 0 |
k 1 |
|
|
a |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
teńligi orınlı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4-qasiyet. f (x) |
funkciyası [a,b] |
segmentinde integrallanıwshı bolsa, onda |
|||||||||||||||||||
|
|
|
|
|
|
|
|
a |
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x)dx f (x)dx, |
a b |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
b |
|
|
a |
|
|
|
|
|
|
|
|
|
|
teńligi orınlı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Dálilleniwi. |
|
|
|
[a,b] |
|
segmentin |
|
T {xk , k |
0, n |
} |
hám |
||||||||||
T {xk |
|
|
|
|
|
|
|
|
|
|
|||||||||||
xn k , k |
0, n |
} |
|
usıllarında |
|
|
|
maydalaymız. |
Bunda |
||||||||||||
a x0 x1 |
xn |
b , |
a xn xn 1 |
|
|
x 0 b |
shártleri |
orınlanǵan. |
|||||||||||||
|
|
|
sáykes { k , k 1, |
|
|
|
|
|
|||||||||||||
Endi |
usı maydalawlarǵa |
|
n}, |
{ k , k 1, n} |
tańlawların |
||||||||||||||||
|
|
|
shárti orınlı bolatuǵınday etip alamız. Bul múmkin, sebebi |
||||||||||||||||||
|
|
||||||||||||||||||||
k n |
k 1, k 1,n |
|
|||||||||||||||||||
f (x) |
funkciyası [a,b] segmentinde integrallanıwshı, integraldıń mánisi [a,b] |
||||||||||||||||||||
segmentin maydalaw usılınan hám tańlaw usılınan ǵárezli emes.
2-sūwret
|
b |
|
|
|
n |
|
|
a |
|
|
|
n |
|
|
Sonda |
f (x)dx lim |
f ( k ) xk |
hám |
f (x)dx |
|
lim |
|
|
|
|||||
|
f ( j ) x j |
|||||||||||||
|
a |
|
(T ) 0 |
k 1 |
|
|
b |
|
(T ) 0 |
j 1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||
boladı. Bunda |
|
|
|
f ( n ) xn , |
|
|
|
|
|
|
|
teńlikleri |
||
f ( 1 ) x1 |
|
, f ( n ) x n f ( 1) x1 |
|
|||||||||||
|
|
a |
|
|
n |
|
|
|
n |
|
|
b |
|
|
orınlı. Demek, |
f (x)dx |
lim f ( j ) x j |
lim f ( k ) xk f (x)dx . |
|
||||||||||
|
|
b |
|
|
(T ) 0 j 1 |
|
|
(T ) 0 k 1 |
|
|
a |
|
|
|
5-qasiyet. |
f (x) |
funkciyası [a,b] |
segmentinde integrallanıwshı bolsa, onda |
|||||||||||
qalegen [a,b] |
segmentine tiyisli x1, x2 , x3 noqatları ushın |
|
|
|
|
|
||||||||
|
|
|
x3 |
|
x2 |
|
x3 |
|
|
|
|
|
|
|
|
|
|
f (x)dx f (x)dx f (x)dx |
|
|
|
|
(5) |
||||||
|
|
|
x1 |
|
x1 |
|
x2 |
|
|
|
|
|
|
|
teńligi orınlı boladı. |
|
|
|
|
|
|
|
|
|
|
|
|
||
Dálilleniwi. Eger |
x1 x2 x3 bolsa, onda 1 hám 2-qasiyetlerden (5) orınlı. |
|||||||||||||
|
|
|
|
|
|
|
x2 |
|
x1 |
|
|
x2 |
|
|
Meyli |
x3 x1 |
x2 bolsın. Onda 2-qasiyetten |
|
f (x)dx f (x)dx |
f (x)dx . |
|||||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
x3 |
|
x3 |
|
|
x1 |
|
|
4-qasiyetten
x3 |
x3 |
x2 |
x3 |
|
f (x)dx f (x)dx f (x)dx |
yamasa f (x)dx |
|
x2 |
x1 |
x1 |
x1 |
Basqa variantlar usıǵan uqsas dálillenedi.
3.Anıq integraldıń teńsiliklerge baylanıslı qasiyetleri.
x2 |
x3 |
|
f (x)dx |
f (x)dx . |
|
|
||
x1 |
x2 |
|
1-qasiyet. f (x) |
funkciyası |
[a,b] |
segmentinde |
integrallanıwshı |
hám |
||||||||
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
x [a,b] ushın |
f (x) 0 bolsa, onda f (x)dx 0 teńsizligi orınlı. |
|
|||||||||||
|
|
|
|
|
|
|
a |
|
|
|
tańlawında |
||
Dálilleniwi. |
[a,b] |
segmentin |
T |
maydalawda hám |
|||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
T ( f , ) f ( k ) xk 0 teńsizligi orınlı. Bul teńsizlikte |
(T ) 0 |
da shekke |
|||||||||||
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
ótip, shektiń teńsizliklerge baylanıslı qasiyetlerinen |
f (x)dx 0 teńsizligine iye |
||||||||||||
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
bolamız. |
|
|
|
|
|
|
|
|
|
|
|
|
|
2-qasiyet. f (x) |
hám g(x) |
funkciyaları [a,b] |
segmentinde integrallanıwshı |
||||||||||
|
|
|
|
|
|
|
|
b |
|
b |
|
|
|
hám x [a,b] |
ushın |
f (x) g(x) |
bolsa, onda f (x)dx g(x)dx |
teńsizligi |
|||||||||
|
|
|
|
|
|
|
|
a |
|
a |
|
|
|
orınlı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Dálilleniwi. |
u(x) f (x) g(x) |
belgilewin |
kiritsek, |
x [a,b] |
ushın |
||||||||
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
u(x) 0 teńsizligi orınlanadı. Onda 1-qasiyetten |
u(x)dx 0 boladı. Bunnan |
||||||||||||
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
b |
|
anıq |
integraldıń |
sızıqlılıq |
qasiyetinen |
paydalanıp, |
|
f (x)dx g(x)dx |
|||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
a |
|
a |
|
teńsizligine iye bolamız. |
|
|
|
|
|
|
|
|
|
||||
3-qasiyet. f (x) funkciyası |
[a,b] |
segmentinde integrallanıwshı, x [a,b] |
|||||||||||
ushın |
f (x) 0 |
teńsizligi orınlı hám keminde bir |
x0 [a,b] noqatı tabılıp, usi |
||||||||||
b
noqatta f (x)
boladı.
Dálilleniwi.
funkciyası úzliksiz hám f (x0 ) 0 bolsa, onda f (x)dx 0
|
a |
Meyli x0 (a,b) |
bolsın. Onda úzliksiz funkciyanıń tańbasın |
0 |
sanı bar boladı da x U (x0 ) [a, b] ushın |
f (x) |
f (x0 ) |
0 |
teńsizligi |
orınli boladı. Endi |
[a, x0 ], |
|
|
||||||
2 |
|
|
|
|
|
|
[x0 , x0 |
], |
[x0 ,b] |
kesindilerin qarastırsaq, |
1-qasiyetten |
||
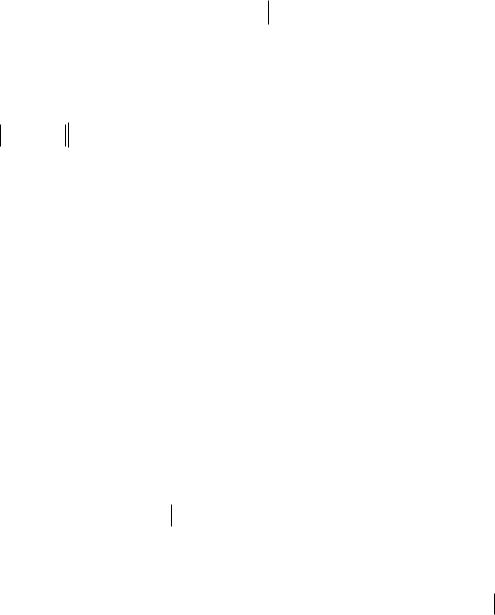
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
||
0 f (x)dx 0 , |
|
|
|
|
|
|
|
|
f (x)dx 0 , |
|
|||||||
|
a |
|
|
|
f (x ) |
|
f (x ) |
x0 |
|
|
x0 |
|
|||||
|
|
|
|
|
|
f (x ) |
|
||||||||||
x0 |
|
x0 |
|
|
|
||||||||||||
f |
(x)dx |
|
0 |
|
dx |
0 |
|
dx |
|
0 |
2 f (x0) 0 |
boladi. |
|||||
|
|
|
|
2 |
|||||||||||||
|
2 |
|
2 |
||||||||||||||
x |
|
|
x |
|
|
|
|
x |
|
|
|
|
|||||
0 |
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||
b |
|
|
x0 |
|
|
x0 |
|
|
|
b |
|
||||||
|
f (x)dx f (x)dx |
f (x)dx |
|
|
f (x)dx f (x0 ) 0 . |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
a |
|
|
|
a |
|
|
x0 |
|
x0 |
|
|
||||||
4. Anıq integraldı bahalaw. |
|
|
|
|
|
|
|||||||||||
|
Teorema. Eger |
f (x) funkciyası |
[a,b] segmentinde integrallanıwshı |
||||||||||||||
onda |
|
f (x) |
|
funkciyasıda [a,b] segmentinde integrallanıwshı hám |
|||||||||||||
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
hám
Onda
bolsa,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x)dx |
f (x) |
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
teńsizligi orınlı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Dálilleniwi. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
u(x) |
|
f (x) |
|
|
belgilewin |
|
|
|
|
|
|
|
|
x |
|
[a,b] |
|
|
ushın |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
kiritip, x , |
|
|
|
|
u(x |
) u(x ) |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
) |
|
|
|
|
|
|
|
|
) |
|
|
|
|
teńsizligi orınlı bolıwın kóremiz. Onda [a,b] |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
f (x |
|
f (x ) |
|
f (x |
|
f (x ) |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
segmentiniń |
T maydalaw |
|
usılında |
|
k [xk 1, xk ], k 1,n |
|
|
|
dara |
|||||||||||||||||||||||||||||||||||||||
kesindilerindegi |
u(x) |
hám |
f (x) |
|
funkciyalarınıń terbelisleri ushın, |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
k (u) sup |
|
u(x |
|
|
|
|
|
) |
|
|
sup |
|
|
|
|
) |
|
|
|
|
k ( f ) , |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
) u(x |
|
|
f (x |
|
f (x ) |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x ,x k |
|
|
|
|
|
|
|
|
|
|
|
x ,x k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
yagnıy k (u) k ( f ), k 1, n |
|
teńsizliklerin jazıw |
|
múmkin. |
Bul teńsizlikler |
|||||||||||||||||||||||||||||||||||||||||||
sistemasındagı |
k |
teńsizlikti |
|
xk |
qa |
kóbeytip, |
|
nátiyjede |
|
kelip |
shıqqan |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
teńsizliklerdi aǵzama-aǵza |
qosıp, |
k (u) xk k ( f ) xk |
|
teńsizligine iye |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
bolamız. f (x) |
funkciyası [a,b] |
|
segmentinde integrallanıwshı bolǵanı ushın bul |
|||||||||||||||||||||||||||||||||||||||||||||
teńsizliktiń |
|
oń tárepi |
(T ) 0 |
|
da nolge umtıladı. Onda onıń shep tárepi de |
|||||||||||||||||||||||||||||||||||||||||||
(T ) 0 |
|
|
da |
nolge umtıladı. |
|
Bul bolsa |
u(x) |
|
f (x) |
|
funkciyası |
|
[a,b] |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
segmentinde integrallanıwshı bolıwı ushın zárúr hám jeterli. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
n |
|
|
|
|
|
|
|
T ( f , ) T ( |
|
|
|||||||||||||||||||||||||
|
|
Endi |
|
|
|
|
f ( ) x |
|
|
|
f ( k ) |
xk |
|
|
|
yamasa |
|
f |
, ) |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
k |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
teńsizliginde (T ) 0 |
da shekke ótsek, u(x) |
hám |
f (x) |
funkciyalarınıń |
||||||
|
|
|
|
|
b |
|
b |
|||
|
|
|
|
|
|
|||||
[a,b] |
segmentinde |
integrallanıwshı bolǵanı |
ushın |
|
f (x)dx |
|
f (x) |
|
dx |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
a |
|
a |
|||
teńsizligi durıs boladı. Teorema dálillendi.

|
f (x) |
|
|
funkciyalarınıń [a,b] |
segmentinde |
integrallanıwshı bolıwınan |
||||||||
f (x) |
|
funkciyalarınıń |
[a,b] |
segmentinde |
integrallanıwshı |
bolıwı |
kelip |
|||||||
|
|
|
|
|
|
|
retinde f (x) |
|
|
|
|
|
||
shıqpaydı. |
Mısal |
|
1, eger x Q, |
funkciyasın |
alsaq, |
onda |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1, eger x J |
|
|
|
||
u(x) |
|
f (x) |
|
1 |
boladı hám ol [a,b] kesindisinde integrallanıwshı, al |
f (x) |
||||||||
|
|
|||||||||||||
funkciyalarınıń ózi [a,b] |
segmentinde integrallanıwshı emes. |
|
|
|||||||||||
Eskertiw. f (x) |
funkciyası shetki noqatları a |
hám b ( a b yamasa |
b a ) |
|||||||||||
bolǵan |
kesindide |
integrallanıwshı |
|
bolsa, onda |
anıq integraldı bahalaw ushın |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
f (x)dx |
|
f (x) |
dx |
|
teńsizliginen paydalanadı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
a |
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Mısal. Eger |
f (x) |
|
funkciyası [a,b] |
|
|
segmentinde integrallanıwshı bolsa, onda |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
, [a,b] |
ushın |
|
f (x)dx |
|
sup |
|
f (x) |
|
b a |
teńsizligin dálilleń. |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
x [a,b] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Sheshiliwi. |
f (x) |
|
|
funkciyası |
|
[a,b] |
segmentinde integrallanıwshı bolgani |
|||||||||||||||||||||||||||||||||||||
ushın bul funkciya [a,b] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
segmentinde shegaralanǵan. Onda |
sup |
f (x) |
bar |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x [a,b] |
|
|
|
|||||||
boladi hám |
x [a,b] |
ushın |
|
|
f (x) |
|
|
sup |
|
f (x) |
|
|
teńsizligi |
orınli bolııwin |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x [a,b] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
esapqa |
|
alsaq, |
|
f (x)dx |
|
|
f (x) |
|
dx |
sup |
|
|
f (x) |
|
dx |
sup |
|
f (x) |
|
|
|
b a |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x [a,b] |
|
|
|
|
|
|
x [a,b] |
|
|
|
|||||||||||||||
boladı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5. Orta mánis haqqında integrallıq teorema. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
Teorema. Meyli, |
f (x) |
hám g(x) |
|
funkciyaları ushın tómendegi shártler |
||||||||||||||||||||||||||||||||||||||||
orınlı bolsın: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1. f (x) |
hám g(x) funkciyaları [a,b] |
|
|
segmentınde integrallanıwshı, |
|
|
|
|||||||||||||||||||||||||||||||||||||||
2. m , M R sanları bar bolıp |
x [a,b] |
|
ushın m f (x) M teńsizligi orınlı. |
|||||||||||||||||||||||||||||||||||||||||||
3. g(x) |
funkciyası [a,b] segmentınde tańbasın saqlaydı, yaǵnıy |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
x [a,b] |
ushın g(x) 0 |
yamasa x [a,b] ushın |
g(x) 0 . |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
Onda sonday [m, M ] sanı bar bolıp, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
f (x)g(x)dx g(x)dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
teńligi orınlı boladı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Dálilleniwi. Meyli x [a,b] |
|
ushın g(x) 0 |
bolsın. Onda m f (x) M |
|||||||||||||||||||||||||||||||||||||||||
teńsizliginen x [a,b] ushın |
|
mg(x) f (x)g(x) Mg(x) |
|
teńsizligi |
kelip |
|||||||||||||||||||||||||||||||||||||||||
shıǵadı. |
|
f (x) |
hám |
|
|
g(x) |
|
funkciyaları |
|
[a,b] |
segmentınde |
integrallanıwshı |
||||||||||||||||||||||||||||||||||
