
Aniq integrallar
.pdfQ.Q. Elgondiev, K. A. Baymuratova, SH. Q. Erejepova, R. D. Narbaeva
ANÍQ INTEGRALLAR HÁM OLARDÍŃ QOLLANÍLÍWLARÍ
MAZMUNÍ
|
Kirisiw……………….…………………………………………………........... |
4 |
|
Anıq integral |
|
1-§. Anıq integraldıń anıqlaması hám bar bolıw shártleri..……………….…...…… |
5 |
|
2-§. Darbu qosındıları………………………………….…………………………... |
9 |
|
3-§. |
Integrallanıwshı funkciyalar klassları…………………………………..……... |
13 |
4-§. Anıq integraldıń qasiyetleri…………………………………………………… |
16 |
|
5-§. Joqarı shegi ózgeriwshi integral. ………………………………….……..…… |
24 |
|
6-§. Anıq integrallardı esaplaw usılları………………………….…………………. |
27 |
|
7-§. Anıq integraldıń geometriyalıq máselelerdı sheshiwde qollanılıwları………... |
32 |
|
8-§. Anıq integraldıń fizikalıq qollanıwları………………………………………… |
53 |
|
|
Menshiksiz integrallar |
|
1-§. Menshiksiz integrallardıń qásiyetleri hám esaplaw usılları…………………… |
65 |
|
2-§. Sheksiz kesindiler boyınsha menshiksiz integrallardıń qásiyetleri……………. |
68 |
|
3-§. Shegaralanbaǵan funkciyalardıń menshiksiz integralları………….………….. |
71 |
|
4-§. Menshiksiz integrallarda ózgeriwshilerdi almastırıw…………………………. |
75 |
|
5-§. Teńsizliklerdi integrallaw……………………………………………………... |
76 |
|
6-§. Teris emes funkciyalardıń menshiksiz integralları. ………….……………….. |
78 |
|
7-§. Menshiksiz integrallardıń absolyut hám shártli jıynaqlılıǵı…………………… |
81 |
|
8-§. |
Menshiksiz integrallar jıynaqlılıǵınıń Abel hám Dirixle |
83 |
|
belgileri………………………………………………………………………... |
|
|
A’debiyatlar…..……………………………………………………………….. |
88 |
ANÍQ INTEGRAL
1-§. Anıq integraldıń anıqlaması hám bar bolıw shártleri a) Iymek sızıqlı trapeciyanıń maydanı.
Meyli f (x) |
funkciyası [a,b] |
segmentinde |
úzliksiz hám |
teris |
emes |
||
anıqlanǵan |
funkciya bolsın, yaǵnıy |
x [a,b] |
úshın |
f (x) 0 |
teńsizligi |
||
orınlansın. |
x a, x b, y 0 tuwrılarınıń kesindileri |
hám |
y f (x) |
||||
funkciyasınıń |
grafigi menen shegaralanǵan G figurasın |
qarastıramız, |
yaǵnıy |
||||
G {(x, y) : a x b, 0 y f (x)}. Bunday figura iymek sızıqlı trapeciya dep
ataladı. [a,b] |
segmentin |
a x0 x1 x2 |
... xn 1 xn b |
|
tеńsizliklеrdi |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
qаnааtlаndiriwshi |
xk , k 0, n |
nоqаtlаrı járdеmindе |
n |
bólekke |
bólemiz |
|||||||||||||||
(maidalaymız) hám bul noqatlardan OY |
kósherine parallel |
tuwrılar ótkeremiz. |
||||||||||||||||||
Sonda G figurası |
Gk {(x, y) : xk 1 x xk , |
|
0 y f (x)}, |
|
|
|
|
n |
||||||||||||
|
k 1,n túrindegi |
|||||||||||||||||||
dаrа trapetciyalarǵa bólinedi. Endi k |
[xk 1, xk ], xk |
xk xk 1, |
|
|
|
|||||||||||||||
k 1, n |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
belgilewlerin |
kiritip, |
k k , k 1, n |
noqatların |
alamız |
da |
|||||||||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f ( k ) xk |
qosındısın |
dúzemiz. |
Bul |
qosındınıń |
mánisi |
[a,b] |
||||||||||||||
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
maydalawdan, k |
|
||||||||||||||||
segmentin xk , k 0,n nоqаtlаrı menen |
noqatların tańlawdan |
|||||||||||||||||||
ǵárezli hám |
n tuwrı múyeshliklerinen ibarat bolǵan teksheli figuranıń maydanına |
|||||||||||||||||||
teń boladı. |
Eger |
G figurası |
jeterli dárejede |
kishi maydalansa |
onda teksheli |
|||||||||||||||
figuranıń maidanınıń iymek sızıqlı trapeciyanıń maydanınan |
parqı judá kem |
|||||||||||||||||||
bolıwı túsinikli. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
[a,b] segmentiniń maydalaw noqatları sanın sonday arttıramız, nátiyjede |
||||||||||||||||||||
k [xk 1, xk ] kesindileri uzınlıqlarınan eń ulkeni nolge umtılsın. Eger usınday
n |
|
jaǵdayda f ( k ) xk qosındısınıń |
segmentin maydalaw usılınan hám |
k 1 |
|
k noqatların tańlawdan ǵárezli bolmaǵan S |
shegi bar bolsa, onda bul shekti G |
figurasınıń maydanı retinde qabıl etiw tábiyiy .
b) ózgeriwshi kúshtiń jumısı. Meyli materiallıq noqat OX kósheri boyınsha F kúshi tásiri astında háreketlensin hám kúshtiń tásir etiw baǵıtı háreket baǵıtı menen birdey bolsın. F kúshin materiallıq noqattıń OX kósherindegi x koordinatasina
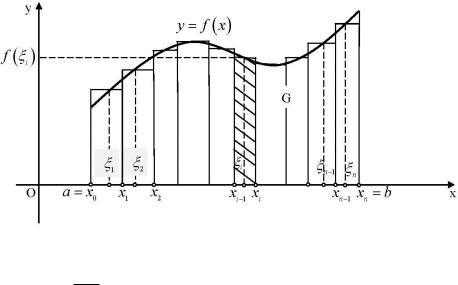
baylanıslı úzliksiz funkciya dep kósherindegi x a noqatınan tabıw máselesin qarastıramız.
esaplap bul kúshtiń materiallıq noqattı OX x b noqatına kóshiriwde orınlagan jumısın
1-suwret
[a,b] segmentin qаnааtlаndiratuǵın xk , k 0, n
k [xk 1, xk ], xk xk xk 1, noqatların alamız. Sonda F
a x0 x1 x2 ... xn 1 xn b shártin nоqаtlаrı járdеmindе n bólekke bólemiz hám
|
|
|
|
|
|
k 1, n belgilewlerin kiritip, |
k k , k 1,n |
|
|||
|
|
kesindisindegi jumısı |
F ( k ) xk a teń. |
||
|
|
n |
|
|
|
Onda F kúshiniń [a,b] segmentindegi jumısı shama menen |
F ( k ) xk |
boladı. |
|||||||||
|
|
|
|
|
|
|
|
|
k 1 |
|
|
Eger [a,b] |
segmentiniń |
|
xk , |
noqatları sanın |
k |
[xk 1, xk ] |
kesindileri |
||||
|
|
|
|
|
|
|
|
|
|
n |
|
uzınlıqlarınan |
eń ulkeni |
nolge |
umtılatuǵınday |
etip |
arttırǵanda F ( k ) xk |
||||||
|
|
|
|
|
|
|
|
|
|
k 1 |
|
qosındısınıń |
A shegi bar bolsa, onda usı shektiń mánisin |
F kúshin materiallıq |
|||||||||
noqattı x a |
noqatınan |
x b |
noqatına kóshiriwdegi |
jumısı |
dep |
atalıwı |
|||||
tábiyiy . |
|
|
|
|
|
|
|
|
|
|
|
Usı qarastırılǵan |
mısallarda |
máseleniń sheshimi integrallıq |
qosındı dep |
||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
atalatuwın f ( k ) xk |
túrindegi qosındısınıń shegin tabıw máselesine keltirildi. |
||||||||||
k 1 |
|
|
|
|
|
|
|
|
|
|
|
Usınday qosındınıń shegin tabıw máselesi texnikanıń, fizikanıń, geometriyanıń, h.t.b. ilim tarawlarınıń kóplegen máselelerinde ushırasadı. Sonıń úshın usınday qosındılarda joqarıdaǵı mısallarda keltirilgendey shekke ótiwdiń nızamli ekenligin tiykarlaw matematikanıń eń ahmiyetli máselelerinen biri bolıp tabıladı.
1. Anıq |
integral |
túsinigi. |
Meyli |
f (x) |
funkciyası |
[a,b] segmentinde |
||
|
|
|
|
|
|
|
|
|
anıqlanǵаn |
hám |
usı segmentke |
tiyisli |
xk , k 0, n |
noqatları úshın |
|||
a x0 x1 x2 ... xn 1 xn b |
teńsizligi orınlanǵan |
bolsın. |
Bul noqatlardı |
|||||

[a,b] segmentin maydalaw dep ataymiz hám olardıń kópligin |
T háribi menen |
||||||
|
|
|
|
|
|
|
|
belgileymiz, yaǵnıy T {xk , k |
|
}. [a,b] segmentin |
xk , k 0, n noqatları |
||||
0,n |
|||||||
|
|
|
|
||||
járdeminde maydalawında kelip shıǵatuǵın k [xk 1, xk ], k |
1, n |
kesindilerine T |
|||||
maydalawındaı dara segmentler dep ataymiz. Meyli xk xk xk 1, k 1, n sáykes
|
|
|
|
|
|
dara segmentleriniń uzınlıqları bolsın. (T) max x |
|
|
|
k |
[x |
k 1 |
, x ], k 1, n |
k |
sanı |
||
|
|
k |
1 k n |
|
||||
|
|
|
|
|
|
|
|
|
T maydalawınıń diametri yamasa maydalı dep ataladı. Eger k k bolsa, onda |
|||||||||||||||||||||
|
|
noqatrları kópligin arqalı belgileymiz hám tańlaw |
dep |
ataladı, |
|||||||||||||||||
, k 1, n |
|||||||||||||||||||||
k |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
f ( k ) xk |
|
f (x) funkciyasınıń |
[a,b] |
|||||||||||||
yaǵnıy { k , k 1,n}. |
qosındısın |
||||||||||||||||||||
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
||||
segmentiniń berilgen T |
maydalawındaǵı hám tayınlanǵan tańlawındaǵı |
||||||||||||||||||||
integrallıq qosındısı |
dep |
ataladı hám |
T ( , f ) |
yamasa T ( ) |
túrinde |
||||||||||||||||
belgileydi, yaǵnıy |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
T ( , f ) T ( ) f ( k ) xk . |
|
|
|
(1) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
||||
1-anıqlama. J |
sanı |
f (x) |
funkciyasınıń [a,b] |
segmenti |
boyınsha anıq |
||||||||||||||||
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
integralı dep ataladı hám f (x)dx |
túrinde belgilenedi, eger 0 sanına sonday |
||||||||||||||||||||
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( ) 0 sanı bar bolıp, |
[a,b] |
segmentiniń diametri |
(T ) |
bolatuǵın T |
|||||||||||||||||
maydalawı hám tańlawı ushın |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T ( , f ) J |
|
|
|
T ( ) J |
|
|
|
f ( k ) xk J |
|
|
(2) |
||||||
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
teńsizligi orınlı bolsa. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Bul anıqlamadan shektiń anıqlamasınan kelip shıqqan halda anıq integral
T ( ) integrallıq qosındısınıń |
(T ) 0 |
jaǵdaydaǵı shegi hám bul shektiń [a,b] |
|||
segmentiniń diametri (T ) |
bolatuǵın |
T maydalawınan hám tańlawınan |
|||
ǵárezli emesligin názerge alǵan halda, |
|
|
|
||
|
|
|
b |
|
|
|
J |
lim |
|
|
(3) |
|
|
(T ) 0 T ( ) f (x)dx |
|
||
|
|
|
a |
|
|
teńligi orınlı bolıwın kóremiz. |
|
|
|
|
|
2-anıqlama. Eger (3) shegi bar bolsa, onda |
f (x) funkciyası [a,b] |
segmenti |
|||
boyınsha |
integrallanıwshı |
yamasa |
[a,b] |
segmentinde Riman |
boyınsha |
integrallanıwshı funkciya dep ataladı. Usı anıqlamadan kelip shıqqan halda f (x) segmenti boyınsha integralı bar dep aytamız.
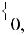
1-teorema(funkciya integrallanıwshı bolıwı zárúrli shárti) Eger f (x) |
||
funkciyası a,b segmenti boyınsha |
integrallanıwshı funkciya |
bolsa, onda ol |
a,b segmentinde shegaralanǵan funkciya boladı. |
|
|
Dálilleniwi. Meyli f (x) funkciyası |
[a,b] segmenti boyınsha |
integrallanıwshı |
funkciya bolsın. Onda 1-anıqlamaǵa sáykes (2)-teńsizligi orınlı. Usi teńsizlikte
1 dep |
esaplap, diametri |
|
|
(T ) (1) |
|
bolǵan T |
maydalawı hám |
|||||||||||||||||
tańlawı ushın |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J T ( , f ) |
|
1 J 1 T ( , f ) J 1 |
|
|
(4) |
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
teńsizligine iye bolamız. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Endi (T ) (1) |
shártin qanaatlandıratuǵın T |
maydalawın tayınlap, |
f (x) |
|||||||||||||||||||||
funkciyası [a,b] |
|
segmentinde shegaralanbaǵan dep esaplaymız. Sonda |
f (x) |
|||||||||||||||||||||
funkciyası |
T |
|
maydalawındaǵı |
k |
dara |
|
segmentlerinen |
keminde |
birinde |
|||||||||||||||
shegaralanbaǵan |
|
|
funkciya |
boladı. |
|
Ulıwmalıqtı |
buzbastan |
f (x) |
funkciyası |
|||||||||||||||
n [xn 1,b] |
|
|
|
segmentinde |
|
|
shegaralanbaǵan |
|
dep |
esaplaymız. |
Endi |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L f ( k ) xk |
|
|||||||||||||
k k , k 1,n 1 |
|
noqatların |
|
tayınlaymız |
hám |
|
belgilewin |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
kiritsek, (4)-teńsizligi |
n n |
ushın |
J 1 f ( ) x L J 1 |
túrinde |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
n |
|
|
|
jazıladı. Bul teńsizlikti |
xn 0 bolǵanı ushın |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
J 1 L |
|
|
|
|
J 1 |
|
|
|
|
|
(5) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
f ( n ) |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
x |
|
x |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
n |
|
|
|
|
|
|
|
túrinde jazıw múmkin. (5)-teńsizligi |
n n |
ushın orınlı |
bolıwınan |
f (x) |
||||||||||||||||||||
funkciyasınıń |
|
n |
[x |
,b] |
segmentinde shegaralanǵan bolıwı kelip shıǵadı. Bul |
|||||||||||||||||||
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
f (x) funkciyasınıń n [xn 1,b] |
|
segmentinde shegaralanbaǵan dep esaplawǵa |
||||||||||||||||||||||
qarama-qarsı. Demek, |
f (x) |
|
tı n |
|
segmentinde shegaralanbaǵan dep esaplaw |
|||||||||||||||||||
qate. Onda onıń qarama-qarsısı durıs, yaǵnıy |
|
f (x) |
funkciyası |
segmentinde |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
shegaralanǵan |
hám sonıń úshın |
[a,b] |
segmentinde shegaralanǵan. Teorema |
|||||||||||||||||||||
dálillendi.
Funkciyanıń kesindide shegaralanǵan bolıwı onıń usı kesindi boyınsha integrallanıwshı bolıwı ushın jeterli emes. Mısal ushın
|
1, |
eger x Q, |
D(x) |
|
|
|
eger x J |
|
|
|

Dirihle funkciyası [0,1] |
segmentinde shegaralanǵan, biraq integrallanıwshı emes. |
||||||||||||||||||||||||||||
Haqiqatında da [0,1] segmentiniń T |
|
|
|
|
|
|
|
k Q} |
|||||||||||||||||||||
maydalanıwında |
{ k , k 1,n; |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
T ( , D) 1 |
|
|
|
|
|
|
||||||||||||
hám { , k 1, n; J} |
tańlawlarında |
sáykes |
|
|
|
|
hám |
||||||||||||||||||||||
|
|
k |
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T ( , D) 0 |
|
bolǵanı ushın |
lim |
T ( , D) shegi bar bolmaydı. |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
(T ) 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
1-mısal. Anıq integraldıń anıqlaması tiykarında dx b a teńligin dálilleń. |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Sheshiliwi. |
bolǵanı ushın [a,b] |
segmentin |
T {x |
k |
, k 0, n} |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f ( k ) 1 |
|
|
|
|
|
||||||||||||||||
usılinda maydalap { k , k 0, n} |
tańlawında |
bolıwın kóremiz. |
|||||||||||||||||||||||||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
b a lim |
|
|
|
|
boladı. |
|
|
|
|
|
|
|||||||||||
Onda T ( ,1) 1 xk |
|
|
|
|
(T ) 0 T ( ,1) b a dx |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
2-§. Darbu qosındıları. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Meyli |
f (x) |
funkciyası [a,b] |
|
segmentinde anıqlanǵan hám shegaralanǵan |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
funkciya, |
[a,b] |
segmenti |
T { |
x , k 0 , |
usılında maydalanǵan |
hám bul |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k dara |
|||||||||||||||||||||||
maydalawda |
k |
[xk 1, xk ], k 1, n |
dara segmentleri payda bolǵan, |
||||||||||||||||||||||||||
segmentiniń |
uzınlıǵı xk ǵa teń edep esaplaymız. |
Sonda |
f (x) funkciyası |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
k [xk 1, xk ], k 1, n |
dara |
segmentlerinde |
qabıl etetuǵın |
manisler kopligi |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
shegaralanǵan boladı. Bunnan |
f (x) |
|
|
funkciyasınıń |
k |
[xk 1, xk ], k 1, n dara |
|||||||||||||||||||||||
segmentlerinde anıq tomengi hám anıq joqarǵı shegaraları bar bolıwın koremiz.
m inf f (x) |
hám |
Mk sup f (x) belgilewlerin kiritip, |
|
||
k |
x k |
|
x k |
|
|
|
|
|
|
||
|
|
|
n |
ST Mk xk |
|
|
|
sT mk xk , |
(1) |
||
|
|
|
k 1 |
k 1 |
|
qosındıların dúzemiz. |
sT , ST |
qosındılarına, f (x) funkciyası ushın |
[a,b] |
||
segmentiniń berilgen T maydalawındaǵı, sáykes tómengi hám joqarǵı Darbu
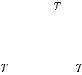
qosındıları dep ataladı. Bul qosındılar T maydalawındaǵı tańlawınan ǵárezli emes hám tómendegi qasiyetlerine iye.
1-qasiyet. [a,b] |
segmentiniń berilgen T maydalawındaı tańlawında |
||||||
|
|
sT T ( ) ST |
(2) |
||||
teńsizligi orınlı. |
|
|
|
|
|
|
|
Dálilleniwi. Anıq joqarı hám anıq tómengi shegaralar anıqlamasınan |
k k |
||||||
|
|
|
|
|
|
|
|
bolǵanı |
ushın mk |
f ( k ) Mk , k 1,n teńsizlikler sisteması orınli. |
Bunnan |
||||
xk 0 |
|
orınlı bolǵanı ushın mk xk f ( k ) xk Mk xk , |
|
|
|
||
teńsizligi |
k 1, n |
||||||
teńsizlikler sisteması kelip shıǵadı. Keyingi sistemanıń teńsizliklerin aǵzama-aǵza
n n n
qosıp, mk xk f ( k ) xk Mk xk teńsizligine iye bolamız. Darbu
k 1 k 1 k 1
qosindıları hám integrallıq qosındı anıqlamalarınan keyingi teńsizliginiń (2)- teńsizlikke teń kushli bolıwın kóremiz.
|
Dálillengen qasiyetten berilgen T maydalawındaǵı tańlawında |
sT ST |
||||||||||||||||||||
teńsizligi orınlı bolıwın kóremiz. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2-qasiyet. [a,b] |
segmentiniń berilgen T maydalawındaǵı múmkin bolǵan |
|||||||||||||||||||||
tańlawlarında |
s |
inf ( ) |
hám |
S |
sup ( ) |
teńlikleri orınli. |
|
|
|
|||||||||||||
T |
|
|
|
T |
|
|
|
T |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dálilleniwi. |
s |
inf ( ) |
teńligin |
dálilleymiz. |
|
Onıń |
ushın infinumnıń |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
anıqlamasına sáykes 1) |
tańlawında |
|
s |
|
T |
( ) |
hám 2) ushın |
0 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
sanı |
ushın sonday |
|
tańlawı bar |
bolıp |
s |
T |
|
T |
( ) |
shártleriniń durıs |
||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bolıwın kórsetiw jeterli boladı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1) |
shárttiń durıslıǵın Darbu qosındılarınıń 1-qasiyetindegi (2) teńsizliginiń shep |
|||||||||||||||||||||
tárepinen kóremiz. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2) |
m inf |
f (x) |
bolǵanı ushın infinumnıń anıqlamasına sáykes |
0 |
||||||||||||||||||
k |
|
|
|
|||||||||||||||||||
|
x k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k k |
|
|
|
|
|
|
|
|
|
f ( k ) mk |
|
|
|
|
|
|||
sanı ushın sonday |
noqatı bar boladı da |
|
|
, k 1, n |
||||||||||||||||||
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b a |
|||
teńsizlikler sisteması orınli boladı. Bul sistemaǵa tiyisli teńsizliklerdi sáykes xk a kóbeyitip nátiyjede payda bolǵan teńsizliklerdi aǵzama-aǵza qossaq,

s |
|
|
|
( |
|
) teńsizlii kelip shıǵadı. Bunda |
|
|
|
||
|
|
|
|
||||||||
T |
T |
|
{ , k 1,n} tańlaw. Demek, |
||||||||
|
|
|
|
|
|
k |
|||||
sT |
inf T ( ) teńligi dálillendi. ST |
sup T ( ) teńligi usıǵan uqsas dálillenedi. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Anıqlama. T2 maydalawı T1 maydalawınıń |
dawamı dep ataladı, eger T1 |
||||||||
maydalawınıń hárbir noqatı T2 |
maydalawınıń da noqatı bolsa. Basqasha aytqanda |
||||||||||
T2 |
maydalawı |
|
T1 maydalawına teń boladı yamasa |
T1 maydalawına keminde bir |
|||||||
taza noqat qosıwdan kelip shıǵadı. |
|
|
|
|
|||||||
|
|
3-qasiyet. Eger T2 maydalawı T1 maydalawınıń dawamı bolsa, onda |
|||||||||
|
|
|
|
|
|
sT |
sT |
ST ST , |
|||
|
|
|
|
|
|
1 |
2 |
2 |
1 |
|
|
yaǵnıy maydalaw noqatlarınıń sanın arttırǵanda Darbudıń tómengi qosındısı kemeymeydi hám joqarı qosındısı artıp ketpeydi.
Dálilleniwi. Bul qаsiyеtti dálillеwdе Т 2 mаydаlаwı Т1 mаydаlаwınа tеk bir tаzа x (xk1, xk ) nоqаtın qоsıw nаtiyjеsindе kеlip shıqqаn jаǵdаydı qаrаstırıw
jеtеrli bоlаdı. Mеyli, |
x |
nоqаtı |
k |
|
dаrа sеgmеntin |
еki |
|
|
|
kеsindilеrinе |
|||||||||||
|
k , |
|
k |
||||||||||||||||||
аjırаtadı, |
olаrdıń uzınlıǵı |
sáykеs 1, 2 |
|
hám |
|
inf |
|
|
|
inf |
f (x) |
||||||||||
|
mk |
f (x), mk |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x k |
|
|
x k |
|
|
bоlsın. |
|
mk , |
|
mk tеńsizliklеrı оrınlı bоlıwın kóriw qıyın еmеs. Оndа |
|||||||||||||||||
mk |
|
mk |
|||||||||||||||||||
sT sT |
|
|
|
|
|
2 ) |
|
|
|
|
|
|
|
|
mk ) 2 0 , |
||||||
mk 1 mk |
2 mk ( 1 |
(mk |
|
mk ) 1 (mk |
|||||||||||||||||
2 |
1 |
|
sT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yaǵnıy |
sT |
tеńsizligi оrınlı. |
ST |
ST |
tеńsizligi usıаn uqsаs dálillеnеdi,al |
||||||||||||||||
|
|
1 |
2 |
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
s2 S2 |
tеńsizliginiń оrinli bоlıwı 1-qasiyette keltirildi. |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
mаydаlаwlаrı ushın |
s |
S |
tеńsizligi оrinli. |
||||||||||
|
|
|
|
|
|
T |
|||||||||||||||
4-qasiyet. T hám |
T |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
Dálilleniwi. Mеyli T mаydаlаwı |
|
|
hám |
T mаydаlаwlаrınıń |
|
dаwаmı |
|||||||||||||||
|
T |
|
|||||||||||||||||||
bоlsın. 3-qasiyette |
Т1 |
Т , Т 2 |
Т |
bоlǵаndа |
sT sT (T ) ST |
tеńsizligi orınlı |
|||||||||||||||
bоlаdı, al |
|
Т1 Т , |
Т2 Т |
bolsa |
ST |
SТ |
tеńsizliginе iyе bоlаmız. Kеyingi |
||||||||||||||
еki tеńsiliklеrdi |
biriktirsek, |
sT |
|
sT |
|
ST |
|
|
|
tеńsizligi |
shıǵаdi. |
Bul |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ST |
|
|
|
|
|
||||
tеńsizlikten sT ST tеńsizliginiń durislıǵı ko’rinip tur. |
|
|
|
|
|
||||||||||||||||
5-qasiyet. Mеyli |
{sT } |
ha’m {ST } |
Dаrbudiń tómеngi |
hám jоqаrǵı |
|||||||||||||||||
qоsındılаrı kópligi bоlsın. Оndа |
f (x) |
funkciyasınıń |
[a, b] kеsindisi boyınsha |
||||||||||||||||||
Dаrbudıń |
|
tómеngi hám |
jоqаrǵı intеgrаllаri dеp |
аtаlаtuǵın |
|
I sup sT |
hám |
||||||||||||||
I inf S |
|
|
|
|
|
|
|
|
|
|
|
s |
I I * S |
T |
|
||||||
sаnlаrı bаr bоlаdı hám bul sаnlаr |
tеńsizligine |
||||||||||||||||||||
T |
|
|
T |
|
|
|
|
|
|
|
|
|
|
T |
|
* |
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
boysınadı.

|
|
|
|
Dálilleniwi. 4-qasiyetten sаnli kópliklеrdiń bir-birinеn аjırаlıwı hаqqındаǵı |
||||||||||||||||||||||||||||||||
tеоrеmаdаn |
|
|
I sup s |
T |
|
hám |
I inf S |
sаnlаrınıń |
|
bаr |
bоlıwı |
kеlip shıǵаdı. |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
T |
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Suprеmum hám infinum |
[a, b] |
kеsindisiniń bаrlıq mumkin bоlǵаn mаydаlаwlаrı |
||||||||||||||||||||||||||||||||||
bоyınshа аlınаdı |
hám |
|
T , |
T |
mаydаlаwlаrında |
sT I* I * ST |
||||||||||||||||||||||||||||||
boladı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
1-teorema. [a, b] |
sеgmеntindе аniqlаnǵаn |
|
f (x) funkciyasi |
usi sеgmеnttе |
||||||||||||||||||||||||||||
intеgrаllanıwshı bоlıwı ushın onıń usı sеgmеntte shegaralanǵan bolıwı hám |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim (ST |
sT ) 0 |
|
|
|
|
|
|
|
|
|
|
(3) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(T ) 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yamаsа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim n1 g(x ) 0 |
|
|
|
|
|
|
|
|
|
(4) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 k 0 |
|
|
|
|
k ( f ) sup f (x) inf |
|
||||||||||||||
tеńliginiń оrinlı bоlıwı zárúr hám jеterlı. Bundaǵı |
|
f (x) |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x k |
|
|
|
|
x k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sanı f (x) |
funkciyasınıń k |
[xk 1, xk ] |
kesindisindegi terbelisi dep ataladı. |
|
||||||||||||||||||||||||||||||||
|
|
|
|
Dálilleniwi. |
Zárúrligi. |
Meyli |
f (x) |
funkciyası |
[a,b] |
|
|
|
|
segmentinde |
||||||||||||||||||||||
integrallanıwshı funkciya bolsın. Onda funkciyanıń kesindide |
|
|
|
integrallanıwshı |
||||||||||||||||||||||||||||||||
bolıwınıń |
zárúrli |
shártine |
sáykes |
f (x) |
funkciyası |
[a,b] |
|
segmentinde |
||||||||||||||||||||||||||||
shegaralanǵan hám anıq integraldıń |
anıqlamasınan |
|
sonday |
|
|
|
J |
sanı tabılıp, |
||||||||||||||||||||||||||||
0 sanına sonday |
( ) 0 sanı bar boladı da |
[a,b] |
segmentiniń |
|||||||||||||||||||||||||||||||||
diametri |
|
|
(T ) |
bolatuǵın |
|
T |
maydalanıwı |
hám |
|
|
tańlawı |
ushın |
||||||||||||||||||||||||
|
|
T ( ) J |
|
|
|
|
teńsizligi |
|
orınlanadı. Bunnan |
J |
|
|
|
T ( ) J |
|
|
|
|
bolǵanı |
ushın |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
3 |
3 |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Darbu |
|
|
|
|
qosındılarınıń |
|
2-qasiyetinen |
|
|
|
J |
|
inf T ( ) sT |
hám |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
T |
sup |
( ) J |
|
teńsizliklerin jazıw múmkin. Bul teńsizlikler hám Darbu |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
T |
|
|
|
|
3 |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
qosındılarınıń 1-qasiyetinen |
J |
3 |
sT |
ST J |
3 |
|
teńsizligine iye bolamız. Onda |
|||||||||||||||||||||||||||||
0 S s 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 ( ) 0: |
||||||||||||||||||||
teńsizligi |
kelip |
shıgadı, yaǵnıy |
||||||||||||||||||||||||||||||||||
|
|
|
|
T |
T |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
0 ST sT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
(T ) , |
|
T , |
bolǵanı |
|
ushın |
shektiń |
|
anıqlamasınan |
||||||||||||||||||||||||||||
|
|
lim (ST |
|
|
sT ) 0 teńligine iye bolamız. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
(T ) 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
