
Лабораторная работа №4
.pdf
МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА» (СПбГУТ)
Факультет Инфокоммуникационных сетей и систем
Кафедра Защищенных систем связи
Дисциплина Математические основы защиты информации
ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №4
Расширенный алгоритм Евклида. Расширенный бинарный алгоритм Евклида
(тема отчета)
Информационная безопасность (10.03.01)
(код и наименование направления/специальности)
Студент: |
|
|
|
Ерохин А.Г. |
ИКБ-03 |
||
(Ф.И.О.) |
|
|
(подпись) |
Студент: |
|
|
|
Чистяков А.С. |
ИКБ-03 |
||
(Ф.И.О.) |
|
|
(подпись) |
Студент:
Пантюхин М.А. ИКБ-03
(Ф.И.О.) (подпись)
К.тех.н, доцент кафедры ЗСС: Кушнир Д.В.
(Ф.И.О.) (подпись)
Санкт-Петербург
2022
Часть 1. Расширенный алгоритм Евклида.
Кроме вычисления d=НОД(a, b), алгоритм Эвклида позволяет дополнительно определить два целых числа α и β, таких что:
+ = - соотношение Безу; α и β – коэффициенты Безу.
Замечание, «почти всегда» если α положительна, то β отрицательно и наоборот.
Алгоритм в общем виде: |
|
|
|
Найти: НОД(a, b) |
|
|
|
= 1 + 1 |
и |
1 |
= 1 + 1 |
= 1 2 + 2 |
и |
2 |
= 2 + 2 |
………………………………………………………………………
|
= |
|
+ |
и |
= |
+ |
−3 |
−2 |
−1 |
−1 |
−1 |
−1 |
−1 |
|
= |
|
|
|
|
|
−2 |
−1 |
|
|
|
|
|
= 0
Ответ: НОД(a, b)= −1
Задание 1. Выполнить «вручную» расширенный алгоритм Евклида
1.Необходимо выбрать свой вариант (варианты) (вариант определяется номером студента в списке группы, если в бригаде несколько человек, то необходимо выполнить соответствующее число соответствующих вариантов).
2.Выполнить «вручную» расширенный алгоритмом Евклида.
Вариант 7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
a = 22, b = 56 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
A |
|
B |
|
q |
|
R |
|
|
12 |
= |
56 |
+ |
(-2) |
* |
22 |
|
||
22 |
= |
56 |
* |
0 |
+ |
56 |
|
|
10 |
= |
22 |
+ |
(-1) |
* |
12 |
|
||
56 |
= |
22 |
* |
2 |
+ |
12 |
|
|
2 |
= |
12 |
+ |
(-1) |
* |
10 |
|
||
22 |
= |
12 |
* |
1 |
+ |
10 |
2 |
= 56 +(-2) * 22+ |
(-1) * (22 + (-1) * (56 + (-2) * 22) |
|||||||||
12 |
= |
10 |
* |
1 |
+ |
2 |
||||||||||||
2 |
= 56 +(-2) * 22+ |
(-1) * (56 * (-1) + 3 * 22) |
||||||||||||||||
10 |
= |
2 |
* |
5 |
+ |
0 |
||||||||||||
2 |
= 56 +(-2) * 22+ |
56 + (-3) * 22 |
||||||||||||||||
|
|
|
|
|
|
|
2 = (-5) * 22 + 2 * 56 |
|
|
|
||||||||
Ответ: НОД(22;56) = 2; α = -5 и β = 2
2
Вариант 17. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
a = 34, b = 20 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
A |
|
B |
|
q |
|
R |
|
14 |
= |
34 |
+ |
(-1) |
* |
20 |
|
|
34 |
= |
20 |
* |
1 |
+ |
14 |
|
6 |
= |
20 |
+ |
(-1) |
* |
14 |
|
|
20 |
= |
14 |
* |
1 |
+ |
6 |
|
2 |
= |
14 |
+ |
(-2) |
* |
6 |
|
|
14 |
= |
6 |
* |
2 |
+ |
2 |
2 = 14 + (-2) * (20 + (-1) * (34 + (-1) * 20) |
|||||||||
6 |
= |
2 |
* |
3 |
+ |
0 |
||||||||||
2 = 34 + (-1) * 20 + (-2) * (2 * 20 + (-1) * 34) |
||||||||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
2 = 34 + (-1) * 20 + (-4) * 20 + 2 * 34 |
|||||||||
|
|
|
|
|
|
|
2 = 3 * 34 + (-5) * 20 |
|
|
|||||||
Ответ: НОД(34;20) = 2; α = 3 и β = -5 |
||||||||||||||||
Вариант 24. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
a = 18, b = 52 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
A |
|
B |
|
q |
|
R |
|
16 |
= |
52 |
+ |
(-2) |
* |
18 |
|
|
18 |
= |
52 |
* |
0 |
+ |
52 |
|
2 |
= |
18 |
+ |
(-1) |
* |
16 |
|
|
52 |
= |
18 |
* |
2 |
+ |
16 |
2 = 18 + (-1) * (52 + (-2) * 18)) |
|||||||||
18 |
= |
16 |
* |
1 |
+ |
2 |
2 = 18 + (-1) * 52 + 2 * 18 |
|
||||||||
16 |
= |
2 |
* |
8 |
+ |
0 |
2 = 3 * 18 + (-1) * 52 |
|
|
|||||||
Ответ: НОД(18;52) = 2; α = 3 и β = -1
Задание 2. Выполнить «программно» расширенный алгоритм Евклида
1.Необходимо выбрать свой вариант (варианты) (вариант определяется номером студента в списке группы, если в бригаде несколько человек, то необходимо выполнить соответствующее число соответствующих вариантов).
2.Выполнить вычисление расширенного алгоритма Евклида в среде Excel или в любой другой программной среде, которая позволяет выводить промежуточные шаги выполнения алгоритма.
Для данного задания была написана программа на языке программирования С++, выполняющая расширенный алгоритм Евклида, с отображением всех промежуточных вычислений.
3
Листинг:
#include <iostream>
using namespace std;
class Euclid {
int A, B, x_new, y_new;
int x_old_2 = 1, y_old_2 = 0, x_old_1 = 0, y_old_1 = 1; public:
Euclid(int _a, int _b) { if (_a >= _b) {
A = _a; B = _b;
}
else {
A = _b; B = _a;
}
cout.width(35); cout << " | "; cout.width(16); cout << x_old_2; cout.width(19); cout << " | "; cout.width(16); cout << y_old_2; cout.width(19);
cout << " | " << endl;
cout.width(35); cout << " | "; cout.width(16); cout << x_old_1; cout.width(19); cout << " | "; cout.width(16); cout << y_old_1; cout.width(19);
cout << " | " << endl;
int q = A / B; int R = A % B;
x_new = x_old_2 - q * x_old_1; y_new = y_old_2 - q * y_old_1; x_old_2 = x_old_1;
x_old_1 = x_new; y_old_2 = y_old_1; y_old_1 = y_new;
while (R > 0) { cout.width(7);
cout << A << " = ";
4
cout.width(7); cout << B << " * "; cout.width(2); cout << q << " + "; cout.width(7); cout << R; cout.width(2); cout << " | ";
A = B;
B = R;
q = A / B; R = A % B;
cout.width(7);
cout << x_old_2 << " - "; cout.width(2);
cout << q << " * "; cout.width(7);
cout << x_old_1 << " = "; cout.width(7);
cout << x_new << " | ";
cout.width(7);
cout << y_old_2 << " - "; cout.width(2);
cout << q << " * "; cout.width(7);
cout << y_old_1 << " = "; cout.width(7);
cout << y_new << " | " << endl;
x_new = x_old_2 - q * x_old_1; y_new = y_old_2 - q * y_old_1; x_old_2 = x_old_1;
x_old_1 = x_new; y_old_2 = y_old_1; y_old_1 = y_new;
}
cout << endl;
cout << "НОД(" << _a << ";" << _b << ") = " << B; if (_a >= _b) {
cout << " = " << _a << " * " << x_old_2 << " + " << _b << " * " << y_old_2 << endl; cout << "Коэффициенты Безу: " << x_old_2 << " и " << y_old_2 << endl;
}
else {
cout << " = " << _a << " * " << y_old_2 << " + " << _b << " * " << x_old_2 << endl; cout << "Коэффициенты Безу: " << y_old_2 << " и " << x_old_2 << endl;
}
}
~Euclid() {}
};
5
int main()
{
setlocale(LC_ALL, "Rus"); int a, b;
cout << "Введите A: "; cin >> a;
cout << "Введите B: "; cin >> b;
cout << endl; cout.width(51); cout << "X"; cout.width(35);
cout << "Y" << endl; Euclid Work(a, b);
}
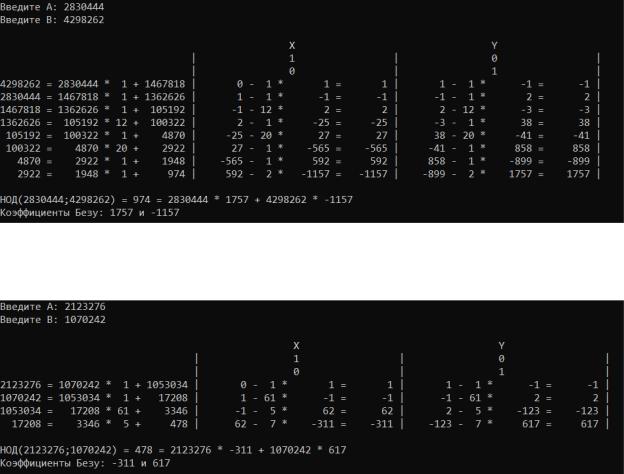
Вариант 7.
a = 2830444, b = 4298262
Вариант 17.
a = 2123276, b = 1070242
6
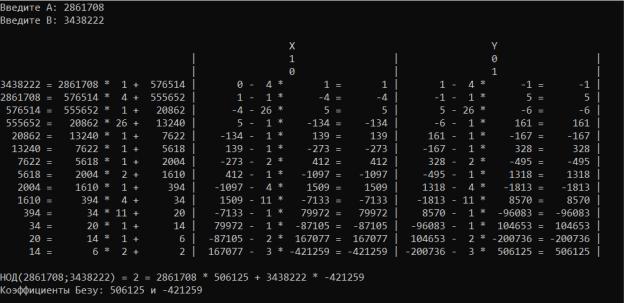
Вариант 24.
a = 2861708, b = 3438222
Часть 2. Обратный и противоположный элемент по модулю.
Нахождение обратного элемента по модулю.
Обратным к числу a по модулю n называется такое число b (обычно обратное к a обозначают как a-1), что: a*b = 1 mod n ( a * −1 = 1 mod n ).
Рассмотрим выражение: a * х + n * y = 1 (это и есть соотношение Безу) возьмём от обеих частей уравнения остаток по модулю n, то получим: a * х = 1 mod n, х – и есть обратный элемент к a.
Пример: m=11, a=3; 4*3+(-1)*11=1; 4*3=1 mod 11, т.е. −1 = 4.
Если получаете отрицательный ответ – переведите в положительный: через n-х.
Нахождение противоположного элемента по модулю.
Противоположным к числу a по модулю n называется такое число b, что: a+b = 0 mod n. b записывают в виде положительного числа.
Задание 3. Найти обратный элемент по модулю.
1. Необходимо выбрать свой вариант (варианты) (вариант определяется номером студента в списке группы, если в бригаде несколько человек, то необходимо выполнить соответствующее число соответствующих вариантов).
2. Найти обратный элемент по модулю.
7
Вариант 7. a = 3, n = 29
−1 = 1 3 −1 = 1 29− =
Вариант 17. a = 13, n = 19
−1 = 1 13 −1 = 1 19− =
Вариант 24. a = 5, n = 17
−1 = 1 5 −1 = 1 17− =
8
