
Физика_электростатика
.pdf
Электростатика
Билет 1.
Основные постулаты электростатики:
1.Существует два типа зарядов – положительные и отрицательные
2.Заряд любого тела или частицы кратен заряду е: = ± , ≈ 1,6 ∙ 10−19Кл
3.Закон сохранения заряда в электрически изолированной системе: ∑ =1 =
4.Инвариантность заряда: заряд системы инвариантен относительно системы отсчёта, т.е. во всех инерциальных системах отсчёта заряд одинаковый.
Закон Кулона:
Сила взаимодействия между неподвижными точечными зарядами пропорционально величине зарядов и
|
1 2 |
|
1 |
|
1 2 |
|
|
−12 Ф |
|||||
обратно пропорционально квадрату расстояния между ними: = |
|
|
|
= |
|
|
|
|
|
; 0 |
= 8,85 ∙ 10 |
|
|
2 |
40 |
|
2 |
|
м |
||||||||
Билет 2.
Напряжённость:
Векторная физическая величина, равная отношению силы , действующей на неподвижный точечный заряд ,
помещённый в данную точку поля, к величине этого заряда .
= |
1 |
|
|
пр |
|||||||
4 |
|
|
2 |
|
|
||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
= |
пр |
|
= |
40 2 |
|||||||
Потенциал:
Физическая величина, равная отношению потенциальной энергии заряда в поле, к величине этого заряда
1 прп = 40
= |
п |
= |
|
|
|
|
|
– потенциал; = |
1→∞ |
|
|
4 |
0 |
|
|
||||||
|
|
|
||||||||
|
пр |
|
|
|
|
|
|
пр |
||
Разность потенциалов:
Величина, равная работе сил поля по перемещению пробного заряда из одной точки в другую, делённую на величину этого заряда.
с = п1 − п2 = пр 1 − пр 2
1→2
1 − 2 = пр
Принцип суперпозиции: Напряжённость поля, создаваемого системой точечных зарядов в данной точке, равна векторной сумме напряженностей полей, создаваемых каждым из зарядов системы в отдельности в
|
|
|
∑ |
|
|
|
|
этой точке. |
|
= |
|
=1 |
|
|
|

Билет 3.
Связь между напряжённостью поля и потенциалом:
= =
= −п; п =
= −
= −
Проекция на оси координат:
|
= − |
|
|
; |
|
= − |
|
; |
|
= − |
|
|
||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
= − ( |
|
+ |
|
+ |
|
|
) |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
= |
|
− |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
- вектор направлен в сторону уменьшения потенциала электрического поля. |
|||||||||||||||||
Билет 4.
Поток вектора напряжённости:
| |
= cos =
∆ ≈ cos ∆ = ∆
= ∑ ∆ ∑ ∆
=1 =1
= ∫ = ∫
Число силовых линий: = = cos =
=
= ∫
|
= |
|
|
|
|
= ∫
}
Теорема Гаусса:
Поток вектора напряжённости электрического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри этой поверхности, делённую на электрическую
постоянную (в вакууме): |
= |
1 ∑ |
|
|
|
=1 |
|
|
|
0 |
|
Билет 5.
Теорема Гаусса:
Поток вектора напряжённости электрического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри этой поверхности, делённую на электрическую
постоянную (в вакууме): |
= |
1 ∑ |
|
|
|
=1 |
|
|
|
0 |
|
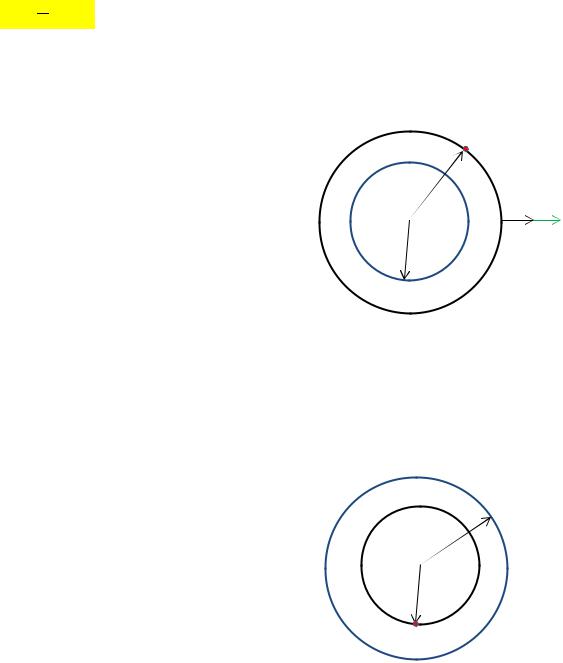
Расчет напряженности и потенциала поля равномерно заряженной сферической поверхности:
1. |
|
Поле вне сферы, r>R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
∫ |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
= |
|
= 42 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
4 |
|
|
= |
|
0 |
|
= 42 0 |
= 40 2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
= |
1→∞ |
; |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
пр |
|
|
|
|
|
|
|
|
|
|
пр |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
∞ |
|
|
|
∞ |
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|||||||||||||||
( ) = |
|
∫ |
|
|
|
|
= ∫ |
|
= ∫ |
|
= ∫ |
|
|
|
|
= |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
4 |
|
2 |
4 |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
пр |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|||||||||||
= |
|
|
|
|
|
|
1 − 2 = |
|
|
( |
1 |
− |
1 |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
40 |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
2. |
|
Поле внутри сферы, r<R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
= |
|
= |
|
= 42 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
= 42 = |
|
|
|
= 0 |
|
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
− |
|
|
= |
|
∫ = 0 |
|
= = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 0 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Билет 6.
Теорема Гаусса:
Поток вектора напряжённости электрического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри этой поверхности, делённую на электрическую
постоянную (в вакууме): |
= |
1 ∑ |
|
|
|
=1 |
|
|
|
0 |
|
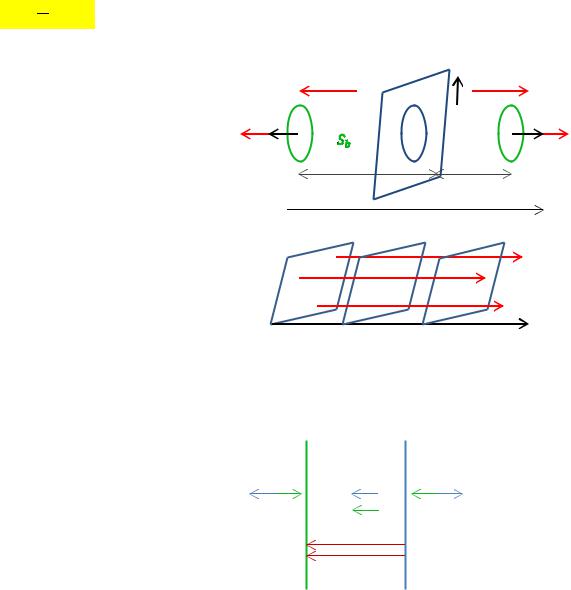
Расчет напряженности и разности потенциалов в поле бесконечной равномерно заряженной плоскости:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
||
|
= |
|
= |
∫ |
+ 2 |
∫ |
= 0 + 2 |
∫ |
= 2 |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|||
|
= 2 |
= |
|
|
|
|
= |
|
; |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
20 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= |
|
|
|
= |
− однородное поле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1′ |
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
( |
− ) |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
− |
|
|
= |
|
∫ |
|
|
+ ∫ |
= 0 + ∫ |
= |
|
|
|
|
+ |
+ |
|
|
|
|
|
|
|||||||||||||||||
1 |
|
|
|
|
2 |
|
1 |
|
|
|
|
1′ |
|
|
|
|
|
1 |
|
|
20 2 |
1 |
|
+ |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
− 2 = |
|
|
( 2 − 1) |
|
|
|
|
|
|
|
|
|
|
|
|
+ + |
1 |
2 |
|
|
|
|
|||||||||||||||||
|
20 |
|
|
|
|
|
|
|
|
|
|
|
+ + |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
Поле двух параллельных равномерно разноимённо заряженных бесконечных пластин:
+ = | −| = =
|
|
|
|
|
|
|
= + + − |
||||
= 2 |
|
= |
|
= |
|
20 |
|
||||
|
|
|
0 |
||
Поле двух параллельных равномерно разноименно заряженных бесконечных плоскостей однородно и сосредоточено в пространстве между плоскостями.
|
− |
|
+ |
|
|
|
|
|
|
|
||||
+ |
− |
+ |
− |
+ |
|
|
|
|
|
|
|
− |
|
|
= 0  = 0
= 0
≠ 0

Билет 7.
Проводники в электрическом поле:
Основные виды проводников: металлы, электролиты, плазма.
Число свободных носителей заряда (электронов) в металлах ~1022 см−3, что составляет примерно один свободный электрон на один атом.
В состоянии равновесия внутри проводника = 0. Если ≠ 0, то свободные носители заряда придут в движение, пока не станет равно 0. Из связи разности потенциалов с напряженностью поля
следует: |
|
− |
|
= ∫ |
= 0 |
|
|
= |
|
= = |
|
1 |
|
2 |
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
Так как у проводника , то вектор напряжённости снаружи проводника перпендикулярен
=
поверхности проводника (силовые линии ортогональны эквипотенциальной поверхности проводника).
1
Теорема Гаусса для любого объёма внутри проводника: = 0 ∫ = 0. Отсюда следует, что = 0 внутри проводника в равновесии. Таким образом, индуцированный или избыточный заряд в равновесии может находиться только на поверхности проводника.
Электроемкость уединенного проводника:
∞
= |
∫ |
|
|
|
||||||
пов |
|
|
|
|
|
|
|
|
|
|
|
|
пов. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
= |
|
|
|
|
= |
|
− электроемкость уединенного проводника |
|
|
|
|||||||||
Электроемкость проводника сферической формы: |
||||||||||
= |
|
|
; = |
|
|
|
= 40 |
|||
4 |
0 |
|
|
|||||||
|
|
|
|
|
|
|
||||
Билет 8.
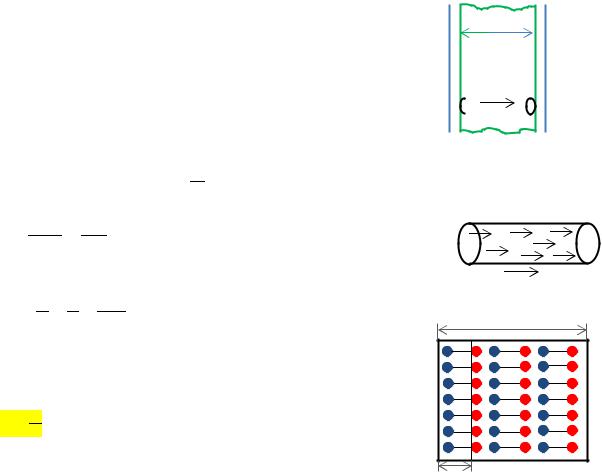
Электрический диполь – система, состоящая из двух разноименных и равных по величине точечных зарядов: + = | −| = . Расстояние между зарядами мало по сравнению с расстоянием до точки наблюдения и называется плечом диполя.
Полярные молекулы – ассиметричное расположение положительных и отрицательных зарядов: 2
Неполярные молекулы – симметричные молекулы, у которых «центры» положительного и отрицательного зарядов совпадают: 2
Поляризация диэлектриков – процесс, в результате которого сумма электрических дипольных моментов молекул ∑ диэлектрика становится отличной от нуля.
Вектор поляризации - векторная физическая величина, равная дипольному моменту единицы объёма
|
∑ |
; |
|
|
вещества, возникающему при его поляризации: = |
∆ |
( = 0) |
||
|
|
|
|
|
Диэлектрическая восприимчивость - физическая величина, мера способности вещества поляризоваться под действием электрического поля:
Билет 9.
Характеристики электрического поля в диэлектриках:
|
|
|
|
1 |
|
|
|
|||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
Вектор напряжённости: = |
пр = |
|
40 2 |
|
|||||||
|
Потенциал электрического поля : |
|
= |
1→∞ |
|
|
||||||
|
|
пр |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||
|
Вектор электрической индукции: |
|
|
|
|
|||||||
|
= 0 + = 0 |
|
||||||||||
Физический смысл диэлектрической проницаемости среды: безразмерная физическая величина,
показывающая во сколько раз электростатическое поле внутри диэлектрика меньше, чем в вакууме.
+ = | −| |
= 0 = |
|
|
|
|
+ |
′ |
+′ |
|||
|
|
|
|
|
− |
|
− |
||||
|
|
|
|
0 |
|
|
|
|
|
|
|
′ = | ′ |
| = ′ ′ |
= |
|
′ |
|
|
′ |
|
|||
|
0 |
|
|||||||||
+ |
− |
|
|
|
|
|
|
|
0 |
||
|
|∑ | |
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
∆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
| | = ; = = ∆
′ |∑ | = = ∆ = ∆ = ′∆
=1
= |
|∑ | |
= |
′∆ |
= ′ |
|
|
|
|
|
||||
|
|
|
|
|
|
|
−′ ∆ |
′ |
|||||
|
|
∆ |
|
∆ |
|
|
|
|
|
|
+ ∆ |
||
= ′ |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
0 |
|
|
|
|
|
|
|||
= 0 |
= |
0 |
= |
0 |
= |
|
|
|
|
|
|||
|
|
|
|
′ |
= 0 − |
′ |
0 = + |
′ |
|
||||
= 0 |
+ |
|
|
|
|||||||||
0 |
= + = (1 + ) = ; |
= 1 + |
−′ = −′ ∆ |
+′ = +′ ∆ |
|||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
||
= |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Билет 10.
Характеристики электрического поля в диэлектриках:
|
|
|
|
1 |
|
|
|
|||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
Вектор напряжённости: = |
пр = |
|
40 2 |
|
|||||||
|
Потенциал электрического поля : |
|
= |
1→∞ |
|
|
||||||
|
|
пр |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||
|
Вектор электрической индукции: |
|
|
|
|
|||||||
|
= 0 + = 0 |
|
||||||||||
Вектор электрической индукции: векторная величина, равная сумме вектора напряжённости
|
|
|
электрического поля и вектора поляризации: |
= 0 |
+ |
Теорема Гаусса для вектора электрической индукции:
Поток вектора электрической индукции через любую замкнутую поверхность равен алгебраической сумме свободных зарядов внутри данной поверхности.
|
1 |
|
|
|
|
|
|
|
|
= |
∑ |
|
|
= ∑ |
|
∫ = ∑ |
|||
|
|||||||||
|
0 |
|
|
0 |
|
|
|
|
|
|
=1 |
|
|
=1 |
|
|
=1 |
||
∫ = ∑ − Теорема Гаусса для вектора электрической индукции
=1
Билет 11.
Диэлектрики в электрическом поле: Под действием электрического поля заряды в диэлектрике смещаются на расстояния порядка межатомных из положения равновесия – происходит поляризация диэлектрика – молекулы становятся электрическими диполями, ориентированными положительно заряженными концами по полю. Возникшие заряды называются индукционными, или связанными. Помимо них в диэлектрике могут быть свободные (сторонние) заряды - некомпенсированные макроскопические заряды.
Теорема Гаусса для диэлектрической среды:
Поток вектора напряжённости электрического поля равен алгебраической сумме свободных зарядов отнесённых к диэлектрической проницаемости среды и вакуума: ∫ 0 = 10 ∑=1
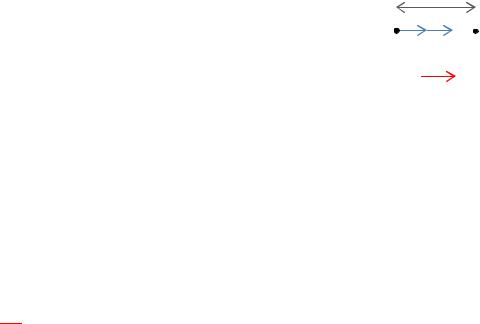
|
|
|
|
Билет 12. |
|
|
|
|
|
Электроемкость плоского конденсатора: |
+ |
|
− |
||||||
|
= − |
1 |
|
|
|
2 |
|||
|
|
|
|||||||
|
|
|
|
||||||
1 |
2 |
|
|
|
|
|
|
||
1 = | 2| |
1 |
|
|
|
|
2 |
|||
= |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
− |
|||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
|
|
|
|
2 |
|
|
|
|
|
|
− |
= ∫ |
= ∫ |
|
|
|||||||
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
− 2 |
= ∫ |
= |
|
= |
|
|
|||||
|
0 |
0 |
||||||||||
|
|
0 |
0 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
− к = |
|
|
= |
0 |
||||||||
|
|
|
|
|
||||||||
1 |
2 |
|
|
|
|
|
|
1 − 2 |
|
|
||
|
|
|
|
|
|
|
|
|
||||
к = 0 − электроемкость плоского конденсатора
Билет 13.
Энергия взаимодействия системы неподвижных точечных зарядов:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||
= |
1 2 |
|
= |
|
|
|
|
= ∑ |
|
= |
|
∑ ∑ |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
12 |
|
|
|
4 |
|
|
|
|
|
|
4 |
|
|
|
|
|
4 |
|
2 |
|
|
4 |
|
|||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
=1 |
0 |
|
|
|
|
=1 =1 |
0 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
≠ |
|
|
|
|
|
|
≠ |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= |
|
|
|
∑ |
∑ |
|
|
|
|
|
|
|
; |
|
|
|
|
|
= |
|
− потенциал, создаваемый в точке расположения |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
2 |
|
|
|
4 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
=1 |
=1 |
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
≠ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
= |
∑ |
∑ |
|
= |
∑ − энергия взаимодействия системы неподвижных точечных зарядов |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
=1 |
=1 |
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
≠
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Билет 14. |
|
|
|
|
|
|
Энергия плоского конденсатора: |
|
|
|
|
|
|||||||||||||||
= |
|
1 |
∑ |
= |
1 |
′ ′ + |
1 |
′′ ′′ |
′ |
|
′′ |
|||||||||
|
|
|
||||||||||||||||||
|
2 |
=1 |
|
|
2 |
|
|
2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
′ = −′′ = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1 |
( ′ − ′′) |
|
|
1 |
|
|
|
|
′ |
|
|
|
|
′′ |
|||||
= |
= |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
2 |
2 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
1 |
= |
|
1 |
2 |
= |
2 |
− энергия плоского конденсатора |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|||||||||||||||
2 |
|
2 |
|
|
|
|
|
|||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
Объемная плотность энергии:
Физическая величина, численно равная отношению потенциальной энергии поля, заключенной в элементе объема, к этому объему:
= = 0 22
Энергия электрического поля:
Так как , тогда
|
|
2 |
|
|
|
|
= ∫ = ∫ |
0 |
= ∫ |
|
− энергия электрического поля |
||
2 |
2 |
|||||
|
|
|
|
|||
|
|
|
||||
