Добавил:

so1zy Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный университет телекоммуникаций им. проф. М.А. Бонч-Бруевича

Предмет:

Физика

Файл:

Физика_механика

.pdf

Скачиваний:

Добавлен:

10.08.2024

Размер:

1.01 Mб

Скачать

☆

1 / 21 2 > Следующая >>>

Механика

Билет 1.

Система отсчёта – совокупность системы координат и часов, связанных с телом, относительно которого изучается движение.

Радиус-вектор — это вектор, идущий из начала координат в заданную точку.

Перемещение — изменение положения физического тела в пространстве с течением времени относительно выбранной системы отсчёта.(вектор соединяющий начальную точку и конечную точку движения тела)

Траектория – линия, описываемая материальной точкой при её движении в пространстве.

Путь – это длина траектории

Средняя скорость по перемещению - вектор, равный отношению перемещения ко времени, за которое оно

совершено: =

Мгновенная скорость – предел, к которому стремится средняя скорость при стремлении промежутка

времени Δt к 0 : =			=
	→0

Среднее ускорение - отношение изменения скорости к промежутку времени, за который это изменении

произошло: =

Мгновенная ускорение – предел, к которому стремится среднее ускорение при стремлении промежутка

времени Δt к 0 : =			=
	→0

Ускорение материальной точки при криволинейном движении:

, где и - единичные вектора

– тангенциальное ускорение

= и =

– нормальное ускорение





R
R


	+

		2
= +	=		+	- ускорение при криволинейном движении

Билет 2.

Угловое перемещение - это угол, на который переместился радиус-вектор при перемещении тела из точки 1 в

точку 2: = − 0

Средняя угловая скорость – вектор, равный отношению углового перемещения ко времени, за которое оно

совершено: =

Мгновенная угловая скорость - предел, к которому стремится средняя угловая скорость при стремлении

промежутка времени Δt к 0: =			=
	→0

Угловое ускорение – характеристика быстроты изменения угловой скорости: =

Связь между линейными и угловыми величинами:

Путь по окружности: =

Связь линейной и угловой скорости: =

( )

Связь тангенциального и углового ускорения:

( )

Связь нормального и углового ускорения: = = 2

Билет 3.

Прямая задача кинематики (поступательное движение) позволяет найти при заданном уравнении траектории скорость и ускорение материальной точки:

Дано:

Решение:

(t) = ( ) + ( ) + ( )

Найти:

−?

= 2

Обратная задача кинематики (поступательное движение) позволяет найти при заданных ускорении или скорости уравнение траектории материальной точки:

		Решение:
Дано:	=
Дано:	=	=


Найти:	−?
Найти:	−?
		= ( ) − ( 0) = ∫ = ∫ ( )
		0	0

		( ) = ( 0) + ∫ ( )
		0
		0

Прямая задача кинематики (вращательное движение) позволяет найти при заданном уравнении траектории скорость и ускорение материальной точки:

Дано:

Решение:

(t) = ( )+ ( ) + ( )

Найти:

−?

+ 2

Обратная задача кинематики (вращательное движение) позволяет найти при заданных ускорении или скорости уравнение траектории материальной точки:

		Решение:
Дано:	=
Дано:	=	=


Найти:	−?
Найти:	−?
		= ( ) − ( 0) = ∫ =	∫ ( )
		0	0

		( ) = ( 0) + ∫ ( )
		0
		0

Билет 4.

Законы Ньютона:

Первый закон Ньютона - тело движется равномерно и прямолинейно или сохраняет состояние покоя, если на него не действуют другие тела (законом инерции). Инерциальная система отсчёта – система отсчёта в которой соблюдается первый закон Ньютона.

Второй закон Ньютона - скорость изменения импульса материальной точки во времени равна


результирующей силе, действующей на материальную точку :			=
результирующей силе, действующей на материальную точку :

Второй закон Ньютона (в другой формулировке) - ускорение, с которым движется материальная точка,

равно отношению результирующей всех сил, действующих на неё, к массе материальной точки:

				=					=
				=					=

Третий закон Ньютона – силы, с которыми две материальные точки действуют друг на друга, имеют одинаковую природу, всегда равны по модулю и направлены в противоположные стороны вдоль


прямой, соединяющей эти точки: 1	= −2; \| 1\| = \| 2\|

Принцип относительности Галилея:

Все инерциальные системы отсчёта эквивалентны друг другу. Никакими механическими опытами, проведёнными в данной инерциальной системе отсчёта, нельзя определить, движется система или нет.

Принцип относительности Эйнштейна:

Уравнения, выражающие законы природы, инвариантны по отношению к любым инерциальным системам отсчета. Инвариантность – неизменность вида уравнения при переходе из одной системы отсчета в другую (при замене координат и времени одной системы – другими).

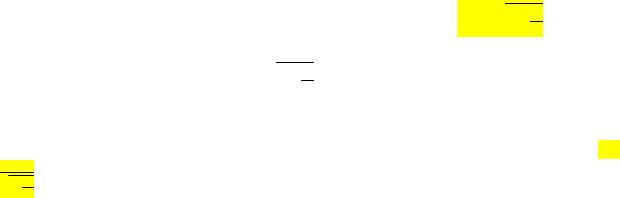
Билет 5.

Границы применимости законов классической механики:

Тела макромира (пространственная протяжённость от размеров больших молекул до размеров Солнечной системы)

Скорость движения много меньше скорости света: (с = 3 108м/с)

Постулаты СТО (Специальной теории относительности):

Постулат 1: Принцип относительности Эйнштейна - Законы природы одинаковы во всех системах координат, движущихся прямолинейно и равномерно друг относительно друга. Это означает, что форма зависимости физических законов от пространственно-временных координат должна быть одинаковой во всех инерциальных системах отсчёта, то есть законы инвариантны относительно переходов между инерциальными система отсчёта.

Постулат 2: Принцип инвариантности скорости света - скорость света в вакууме одинакова во всех системах координат, движущихся прямолинейно и равномерно друг относительно друга.

Следствия из постулатов СТО:

Сокращение линейных размеров т.е. линейный размер тела, движущегося относительно

инерциальной системы отсчёта, уменьшается в направлении движения: = 0√1 − 2 , где 0 – длина

тела в неподвижной системе отсчёта. Для движущегося наблюдателя длина отрезка кажется

уменьшенной в направлении движения в √1 − 2 раз, поперечные размеры тела в обеих системах

одинаковы. Итак, для неподвижного наблюдателя размеры движущегося тела в направлении их движения сокращаются, и тем больше, чем больше скорость движения.

Замедление времени т.е. для движущегося наблюдателя время кажется идущим медленнее: =

0		, где - промежуток времени между двумя событиями в неподвижной системе отсчета. Чем
√1−	2	0
	2
	с2

больше скорость, тем больше замедление времени.

Билет 6.

Второй закон Ньютона:

Скорость изменения импульса материальной точки во времени равна результирующей силе, действующей на

материальную точку : =

Второй закон Ньютона (в другой формулировке):

Ускорение, с которым движется материальная

точка,

равно отношению результирующей всех сил,

действующих на неё, к массе материальной точки:

Движение центра инерции тела:

Центр инерции тела (системы тел) движется так, как двигалась бы материальная точка с массой m, равной массе тела (системы тел) под действием результирующей всех внешних сил, приложенных к телу (системе

тел):

∑

(

) =

Билет 7.

Третий закон Ньютона:

Силы, с которыми две материальные точки действуют друг на друга, имеют одинаковую природу, всегда

равны по модулю и направлены в противоположные стороны вдоль прямой, соединяющей эти точки: 1

−2;

| 1| = | 2|

Закона изменения импульса:

Изменение импульса системы материальных точек за некоторый промежуток времени равно импульсу

результирующей всех внешних сил, действующих на систему за этот промежуток времени:

Закон сохранения импульса:

Сумма импульсов всех тел системы есть величина постоянная, если векторная сумма внешних сил,

действующих на систему тел, равна нулю: при = 0 следует

Закон сохранения импульса формулируют для замкнутой системы тел - системы, на которую не действуют

внешние силы: импульс замкнутой системы тел есть величина постоянная.

Реактивное движение:

Движение тела, возникающее при отделении некоторой его части с определённой скоростью относительно

него. При этом тело получает импульс в противоположном направлении, равный импульсу отделившейся

= −

, где

– масса ракеты

части. Закон сохранения импульса для реактивного движения:

– её ускорение

– скорость истечение

газов

– расход массы

топлива в единицу

времени

Билет 8.

Момент импульса материальной точки относительно некоторого начала отсчёта определяется векторным

	( = sin = )
произведением её радиус-вектора и импульса: = [ х ]
Величина момента импульса относительно оси z равна:	= sin	= = 2

	2

Момент силы – векторная величина, определяемая векторным произведением радиус-вектора и вектора

силы: = [ х ] ( = sin = )

Уравнение моментов для системы материальных точек:

системы

= ∑

= ∑ ∑

+ ∑

=1 =1

≠

= 0 ;

− сумма моментов внешних сил

∑ ∑

∑

=1 =1

≠

∑

= ∑

∑

= ∑

−уравнение моментов для системы материальных точек

Закон сохранения момента импульса:

Суммарный момент импульса системы материальных точек относительно точки – величина постоянная, если векторная сумма моментов всех внешних сил относительно точки, действующих на систему, равна 0.

Билет 9.

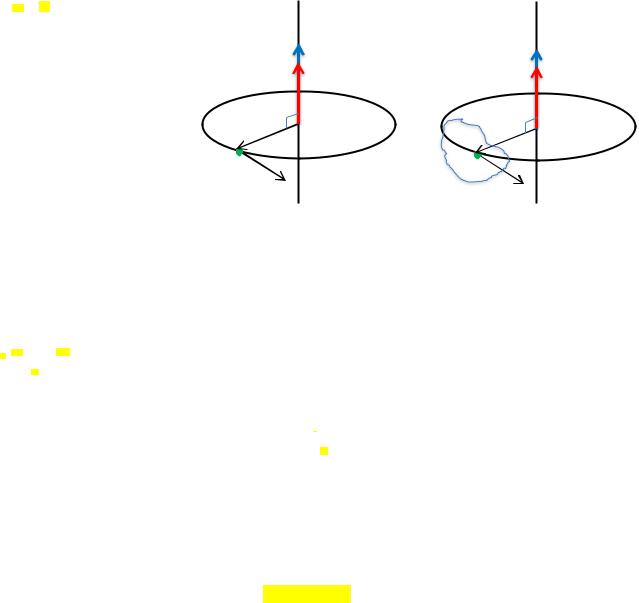
Момент инерции материальной точки относительно неподвижной оси – физическая величина, равная произведению массы материальной точки на квадрат расстояния, от материальной точки до оси вращения:

			=		2

	0

Момент инерции для абсолютно твёрдого тела:

= ∑

∑

Если

и , тогда

= ∫ 2 = ∫ 2 =

= ∑

∫

Теорема Штейнера:

Момент инерции твёрдого тела путём интегрирования по V

Момент инерции тела относительно произвольной оси z равен сумме момента инерции этого тела относительно оси, параллельной данной и проходящей через центр масс этого тела, и произведения массы

тела на квадрат расстояния между осями:	=	+ 2

Билет 10.

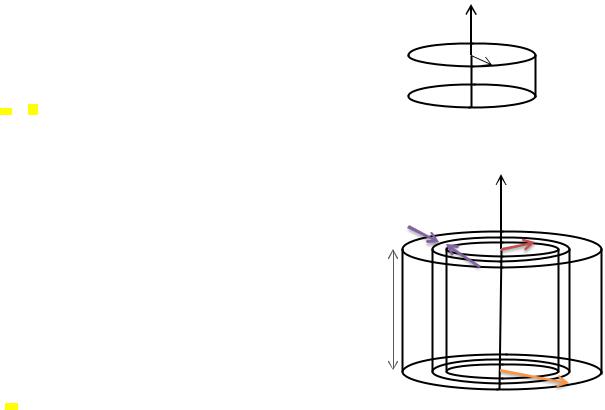
Момент инерции тонкостенного кольца:

Найдём момент инерции относительно оси симметрии:

= ∑

2 = ∑

= 2 ∑

= 2; = 2

Ответ:

Момент инерции сплошного цилиндра:

Найдём момент инерции относительно оси симметрии,

проходящей через центр масс:

∫

= 2

2 2 = 2

3 = 2

∫0

2 = ; = =				2


				2
				2
Ответ:	=		2

		2
		2

Билет 11.

Основное уравнение динамики вращательного движения:

Абсолютно твердое тело, вращающееся относительно неподвижной оси. Момент импульса тела относительно

оси:

Скорость изменения момента импульса:

Учитывая, что

= , то

= , а

- основное уравнение вращательного движения

Угловое ускорение тела прямо пропорционально сумме моментов внешних сил, действующих на тело, и обратно пропорционально моменту инерции тела.

1 / 21 2 > Следующая >>>

Соседние файлы в предмете Физика

#
10.08.20241.01 Mб1Физика_механика.pdf
#
10.08.20242.55 Mб0Физика_термодинамика.pdf
#
10.08.2024709.81 Кб0Физика_электрический_ток.pdf
#
10.08.2024957.4 Кб1Физика_электростатика.pdf