МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА» (СПбГУТ)

Факультет Инфокоммуникационных сетей и систем Кафедра Защищенных систем связи

Дисциплина Криптографические методы защиты информации

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №16

Исследование криптосистемы с открытым ключом РША

(тема отчета)

Информационная безопасность (10.03.01)

(код и наименование направления/специальности)

Студент группы ИКБ-06:

Ерохин А.Г.

(Ф.И.О.) (подпись)

Д.т.н., проф. каф. ЗСС:

Яковлев В.А.

(Ф.И.О.) (подпись)

Цель работы: Закрепить знания, полученные на лекциях, по теме “ Криптосистема РША”.

Используемое программное обеспечение: Для работы используется программа “RSA”.

Задание:

1. Выполнить упражнения по возведению в степень больших целых чисел по модулю;

2. Произвести генерирование ключей для криптосистемы РША, а также шифрование и дешифрование с ее помощью коротких текстов;

3. Произвести шифрование файлов большого размера безопасной криптосистемой РША и оценить время шифрования и дешифрования при ее простейшей программной реализации;

4. Произвести подписание сообщений и проверку подписи;

5. Осуществить обмен зашифрованными и подписанными сообщениями в локальной сети.

Ход выполнения лабораторной работы:

Часть 1. Закрепление навыков модульных вычислений

1. Рассчитали степени малых чисел по малому модулю и проверим их правильность расчетами на бумаге.

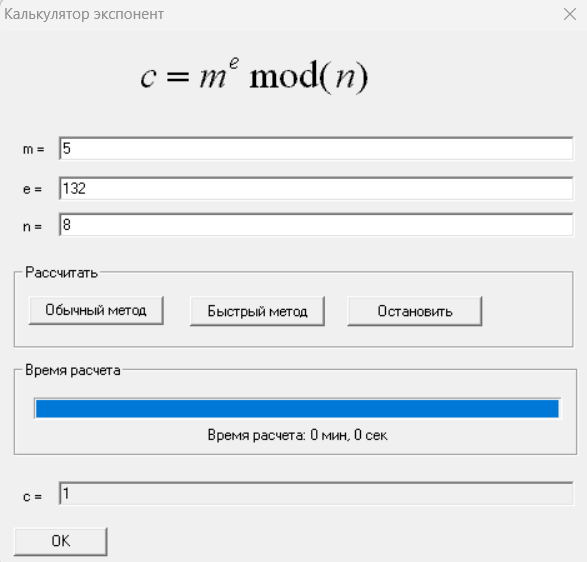
Рисунок 1 – Расчет степени малых чисел по малому модулю

Проверка:

2. Рассчитали степени произвольных больших чисел по модулю прямым методом и быстрым методом. Убедились в эффективности быстрого метода.

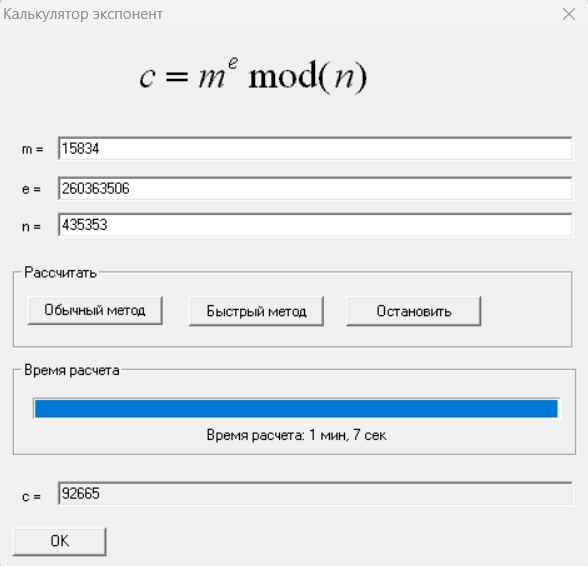
Рисунок 2 – Расчет степени чисел по модулю прямым методом

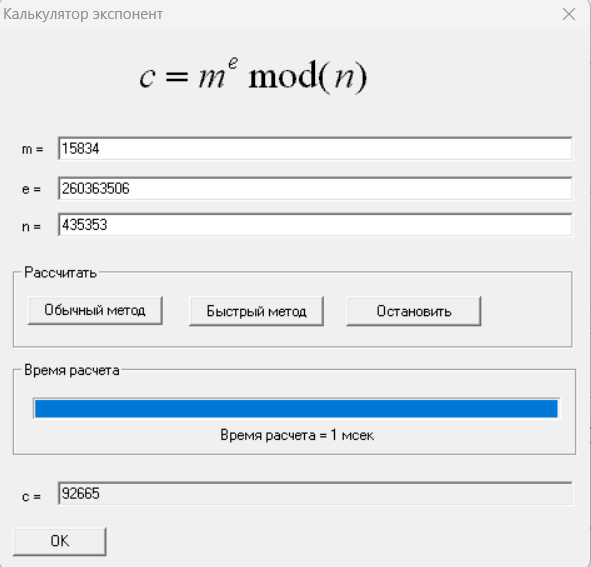
Рисунок 3 – Расчет степени чисел по модулю быстрым методом

Прямой метод: t = 67 c = 67000 мс

Быстрый метод: t = 1 мс

Можно сделать вывод, что быстрый метод более эффективен для нахождения степеней произвольных больших чисел по модулю.

Часть 2. Генерирование ключа в криптосистеме рша

1. Выбрав в главном меню опцию “Генерировать ключи”, задали малые простые числа p, q и сгенерировали ключи для РША. Проверили правильность вычислений расчетами на бумаге.

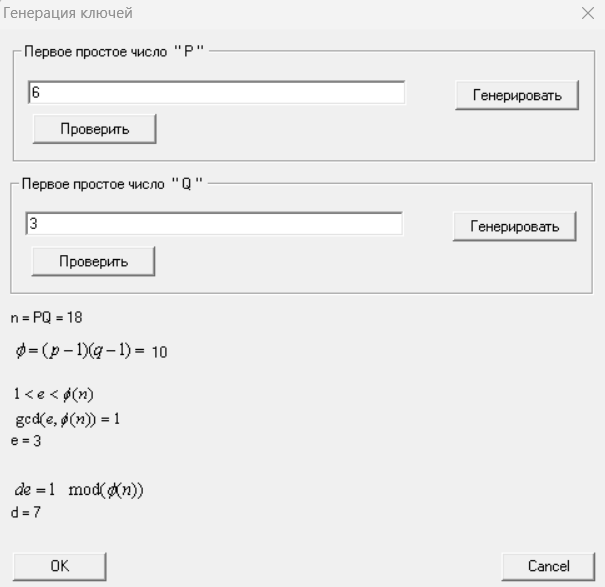
Рисунок 4 – Генерация ключа при малых p и q

Проверка:

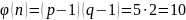
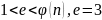
Ищем как обратный элемент к :

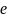Для решения используем расширенный алгоритм Евклида

– закрытый ключ

Проверка:

2. Произвели случайное генерирование простых чисел p,q разрядности по 100 бит каждое, задаваясь количеством проверок n=20 и используя опцию “Генерировать” в подменю “Генерация ключей”. Выполнили затем генерацию ключей для системы РША.

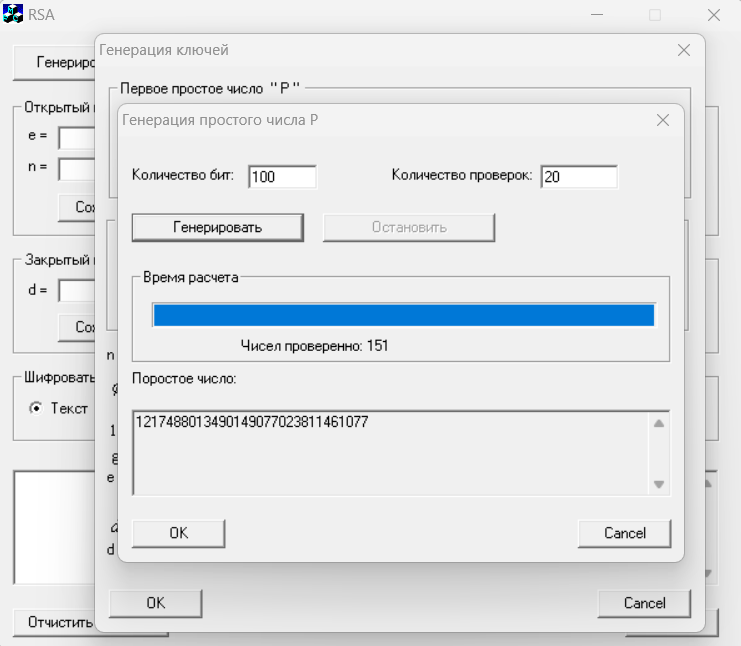
Рисунок 5 – Генерация числа P, при n = 20

P = 1217488013490149077023811461077

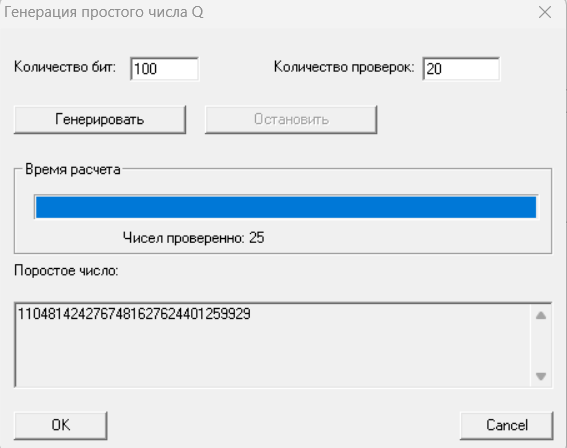
Рисунок 6 – Генерация числа Q, при n = 20

Q = 1104814242767481627624401259929

Рисунок 7 – Генерация ключей

3. Произвели случайное генерирование простых чисел p,q разрядности по 100 бит каждое, задаваясь количеством проверок n=30. Выполнили затем генерацию ключей для системы РША.

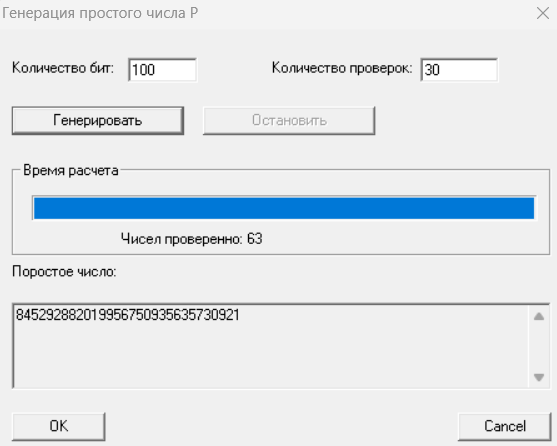
Рисунок 8 – Генерация числа P, при n = 30

P = 845292882019956750935635730921

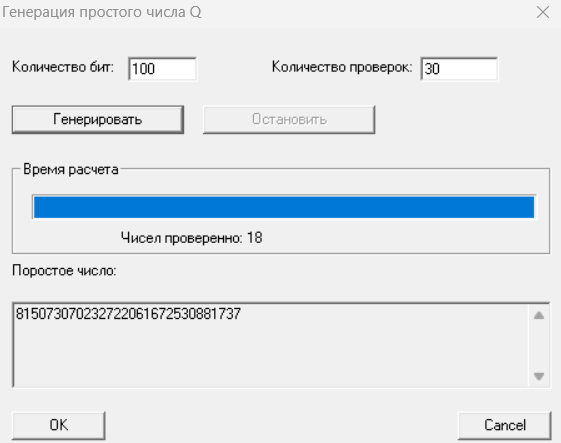
Рисунок 9 – Генерация числа Q, при n = 30

Q = 815073070232722061672530881737

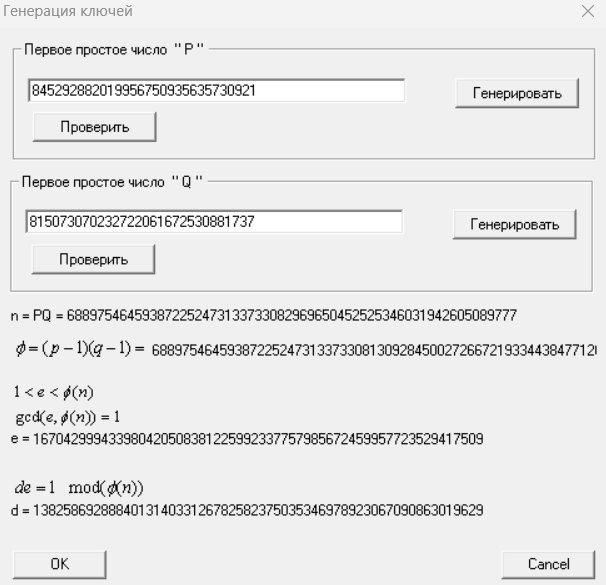
Рисунок 10 – Генерация ключей

Вероятности ошибочного выполнения тестирования простых чисел:

Часть 3. Шифрование сообщений в криптосистеме рша

1. Перейдя в основное меню, произвели шифрование короткого смыслового текста на русском, введенного в левое поле с использованием опции “Зашифровать”.

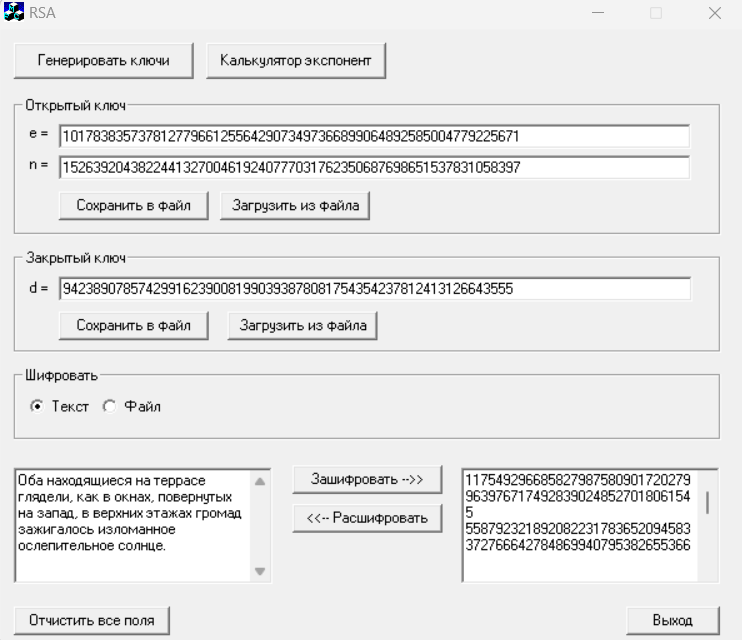
Рисунок 11 – Шифрование текста

2. Удалим открытый текст в левом поле и произведем дешифрование криптограммы, содержащейся в правом поле, используя опцию “Расшифровать”.

Криптограмма:

1175492966858279875809017202799639767174928390248527018061545 558792321892082231783652094583372766642784869940795382655366 43471388715101179899672424968825141175760544098192139541876 318336004173578475558084632829194330735625195727172923623367 31027910730432419727572875056417672060011694189591407389009 761680694098233620360662669535614458932559693893581978563783

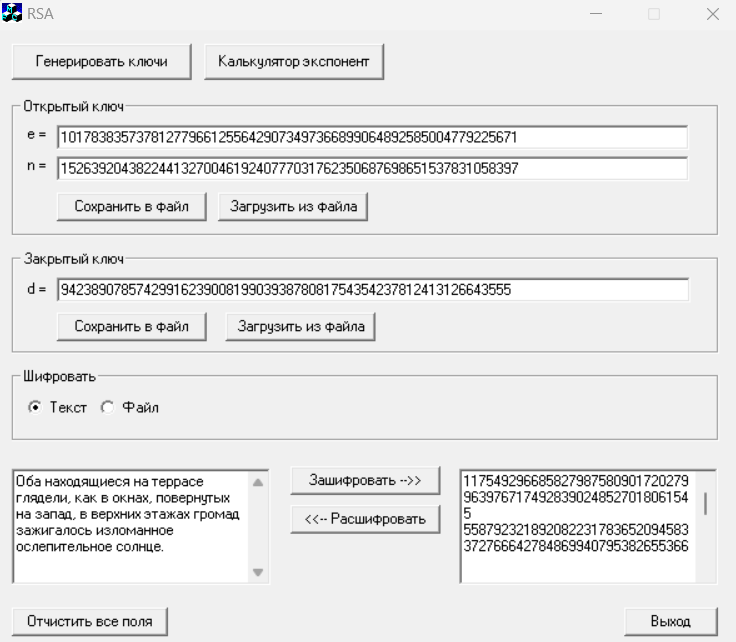
Рисунок 12 – Дешифрование криптограммы

Расшифрованный текст:

Оба находящиеся на террасе глядели, как в окнах, повернутых на запад, в верхних этажах громад зажигалось изломанное ослепительное солнце.

Расшифрованный текст полностью соответствует исходному тексту.

3. После изменения одной из цифр криптограммы, произвели дешифрование.

Криптограмма с ошибкой:

1175492963858279875809017202799639767174928390248527018061545 558792321892082231783652094583372766642784869940795382655366 43471388715101179899672424968825141175760544098192139541876 318336004173578475558084632829194330735625195727172923623367 31027910730432419727572875056417672060011694189591407389009 761680694098233620360662669535614458932559693893581978563783

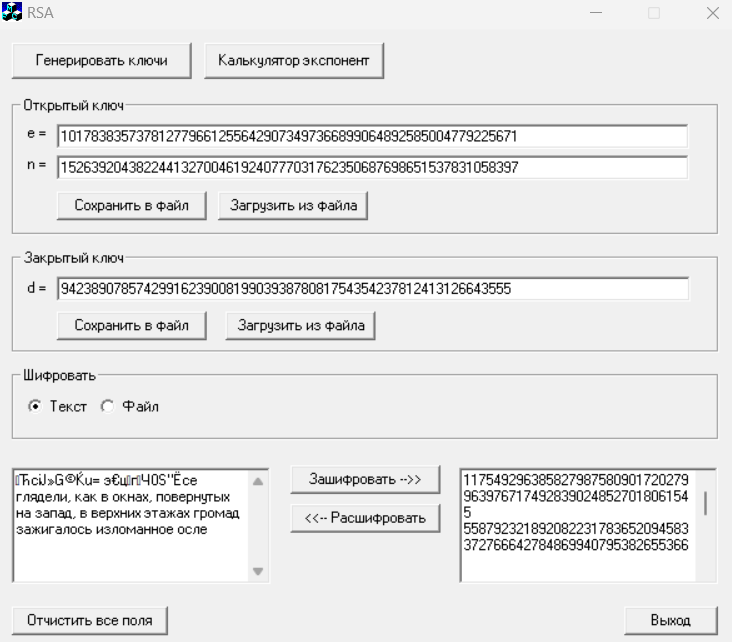
Рисунок 13 – Дешифрование криптограммы с ошибкой

Расшифрованный текст с ошибками:

ЋсіJ»G©Ќu=э€цгЧ0Ѕ"Ёсе глядели, как в окнах, повернутых на запад, в верхних этажах громад зажигалось изломанное осле

Открытый текст:

Оба находящиеся на террасе глядели, как в окнах, повернутых на запад, в верхних этажах громад зажигалось изломанное ослепительное солнце.

Можно сделать вывод, что измененная криптограмма была расшифрована, однако наличие ошибки в криптограмме привело к тому, что кусок текста расшифровался неверно и утратил свой смысл.

4. Сгенерировали простые числа p, q разрядности по 1024 бит, при n=30.

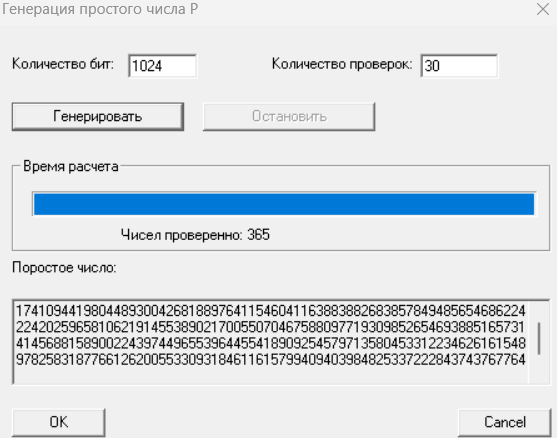
Рисунок 14 – Генерация числа P

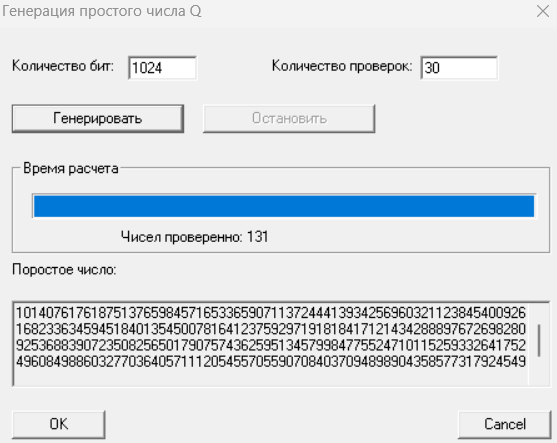
Рисунок 15 – Генерация числа Q

P=174109441980448930042681889764115460411638838826838578494856546862242242025965810621914553890217005507046758809771930985265469388516573141456881589002243974496553964455418909254579713580453312234626161548978258318776612620055330931846116157994094039848253372228437437677644715134376734063848047879058100686801

Q=101407617618751376598457165336590711372444139342569603211238454009261682336345945184013545007816412375929719181841712143428889767269828092536883907235082565017907574362595134579984775524710115259332641752496084988603277036405711120545570559070840370948989043585773179245492189521376993958582981697004585989373

5. Вернувшись в главное меню, произвели шифрование произвольного файла большого объема (не менее 100кбайт), фиксируя при этом время шифрования.

Выберем файл «открытый» размером 135 КБ.

Рисунок 16 – Файл для шифрования

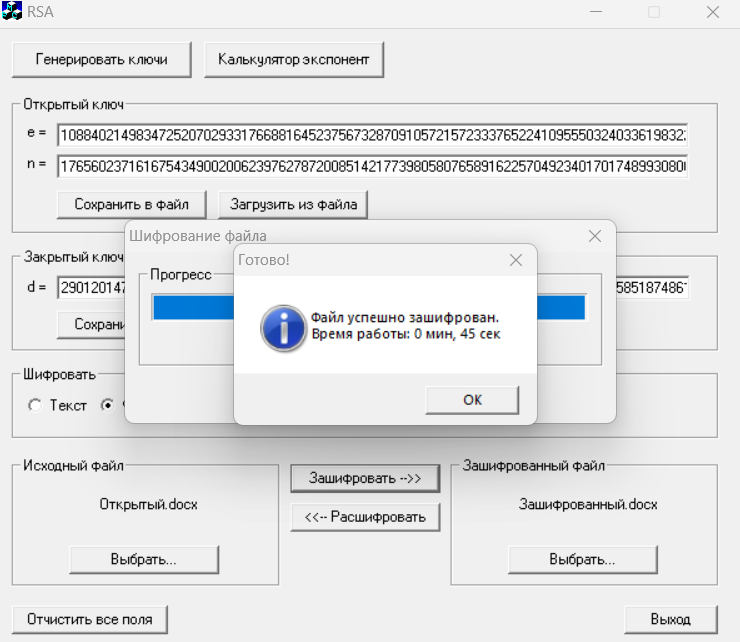
Рисунок 17 – Шифрование файла

Получили в ходе шифрования файл «зашифрованный» размером 137 КБ.

6. Произведем дешифрование криптограммы, полученной в п.5, фиксируя при этом время дешифрования.

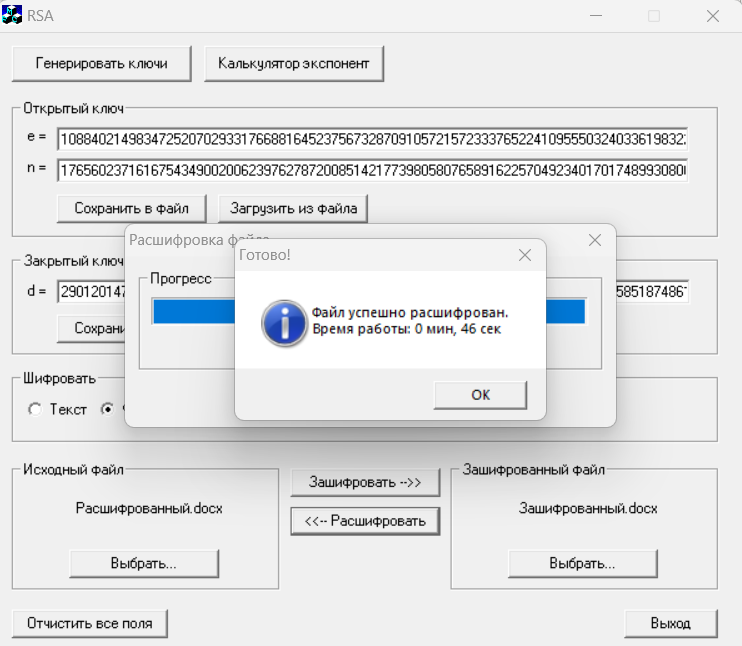
Рисунок 18 – Дешифрование файла

Получили в ходе шифрования файл «расшифрованный» размером 135 КБ.

Рисунок 19 – Расшифрованный файл соответствует исходному

7. По данным п.5,6 рассчитаем скорость шифрования и дешифрования при данной простейшей программной реализации безопасной криптосистемы РША.

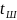= 45 сек – время шифрования.

– скорость шифрования.

= 46 сек – время расшифрования.

– скорость дешифрования.