
Лабораторная работа №11
.docxМИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА» (СПбГУТ)

Факультет Инфокоммуникационных сетей и систем Кафедра Защищенных систем связи
Дисциплина Криптографические методы защиты информации
ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №11
Моделирование работы формирователя случайной гаммы и исследование характеристик гаммы
(тема отчета)
Информационная безопасность (10.03.01)
(код и наименование направления/специальности)
Студент группы ИКБ-06:
Ерохин А.Г.
(Ф.И.О.) (подпись)
Д.т.н., проф. каф. ЗСС:
Яковлев В.А.
(Ф.И.О.) (подпись)
Цель работы: Анализ работы формирователя случайной гаммы и исследование характеристик гаммы.
Задание:
Построить линейный рекуррентный регистр по заданному характеристическому многочлену
 (задан
степенями коэффициентов, см. табл.).
(задан
степенями коэффициентов, см. табл.).Начальное заполнение регистра S=KR, где K- ключ (Ваш номер по журналу, представленный в двоичном виде, младший разряд справа), R –случайное число (если не задано преподавателем, то равно нулю).
Провести моделирование работы ЛРР, представив таблицу смены его состояний.
Исследовать полученную линейную рекуррентную последовательность, определить:
-Период последовательности;
-Баланс единиц и нулей в ней;
-Найти серии и подсчитать их количество;
-Проверить свойство «окна».
-вычислить автокорреляционную функцию.
-Сделать выводы о статистических характеристиках ЛРР.
Выписать найденные параметры в отдельную таблицу, они понадобятся для сравнения с статистическими параметрами шифрующей гаммы.
Провести моделирование работы формирователя случайной гаммы, для этого:
-Подсоединить к ЛРР набор нелинейных элементов в соответствии с заданием (см. рис.).
-Найти случайную последовательность на выходе формирователя.
-Определить баланс, серии, окна для полученной последовательности.
-Найти оценку линейной эквивалентной сложности (ЛЭС) последовательности.
-Найти точное значение линейной эквивалентной сложности. Для этого запустить программу ЛРР2. Ввести в соответствующее поле, полученную последовательность, получить результат. По полученному многочлену построить эквивалентный ЛРР.
-Сделать выводы о характеристиках синтезированного формирователя и его пригодности для шифрования сообщений по показателям увеличения линейной сложности и сохранения статистических характеристик исходной рекуррентной последовательности.
Ход выполнения лабораторной работы:
Лабораторная работа выполняется по вариантам, согласно номеру студента в списке группы – 10 вариант. Исходные данные представлены в таблице 1.
Таблица 1.
№ вар. |
|
Нелинейные узлы: 1,2,3 |
10 |
530 |
И, ИЛИ-НЕ, УЛ |
Построили
линейный рекуррентный регистр по
заданному характеристическому
многочлену  :
:
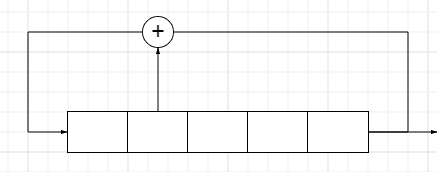
Рисунок 1 – ЛРР
Выбрали начальное заполнение регистра S=KR: 0101000110 = 01100.
Максимальный период рекуррентной последовательности для регистра заданным примитивным многочленом: 25 – 1 = 31 (все комбинации кроме пяти нулей).
Проведем моделирование работы ЛРР, представив таблицу смены его состояний:
№ такта |
Состояние ЛРР |
Выходная последовательность |
Период, T |
||||
5 |
4 |
3 |
2 |
1 |
|||
1 |
0 |
1 |
1 |
0 |
0 |
0110011111000110111010100001001 |
31 |
2 |
1 |
0 |
1 |
1 |
0 |
||
3 |
0 |
1 |
0 |
1 |
1 |
||
4 |
0 |
0 |
1 |
0 |
1 |
||
5 |
1 |
0 |
0 |
1 |
0 |
||
6 |
0 |
1 |
0 |
0 |
1 |
||
7 |
0 |
0 |
1 |
0 |
0 |
||
8 |
0 |
0 |
0 |
1 |
0 |
||
9 |
0 |
0 |
0 |
0 |
1 |
||
10 |
1 |
0 |
0 |
0 |
0 |
||
11 |
0 |
1 |
0 |
0 |
0 |
||
12 |
1 |
0 |
1 |
0 |
0 |
||
13 |
0 |
1 |
0 |
1 |
0 |
||
14 |
1 |
0 |
1 |
0 |
1 |
||
15 |
1 |
1 |
0 |
1 |
0 |
||
16 |
1 |
1 |
1 |
0 |
1 |
||
17 |
0 |
1 |
1 |
1 |
0 |
||
18 |
1 |
0 |
1 |
1 |
1 |
||
19 |
1 |
1 |
0 |
1 |
1 |
||
20 |
0 |
1 |
1 |
0 |
1 |
||
21 |
0 |
0 |
1 |
1 |
0 |
||
22 |
0 |
0 |
0 |
1 |
1 |
||
23 |
1 |
0 |
0 |
0 |
1 |
||
24 |
1 |
1 |
0 |
0 |
0 |
||
25 |
1 |
1 |
1 |
0 |
0 |
||
26 |
1 |
1 |
1 |
1 |
0 |
||
27 |
1 |
1 |
1 |
1 |
1 |
||
28 |
0 |
1 |
1 |
1 |
1 |
||
29 |
0 |
0 |
1 |
1 |
1 |
||
30 |
1 |
0 |
0 |
1 |
1 |
||
31 |
1 |
1 |
0 |
0 |
1 |
||
В результате моделирования ЛРР получили, что максимальный период последовательности равен 31. Исследуем ЛРП:
Линейно рекуррентная последовательность: 0110011111000110111010100001001
Период последовательности: 31
Баланс единиц и нулей: 16 единиц, 15 нулей. Свойство баланса выполняется.
Серии: 8(1), 4(2), 2(3), 1(4), 1(5). Свойство серий выполняется.
Свойство «окна»:
 – выходная
последовательность.
– выходная
последовательность.
Окна длиной 5: 01100, 11001, 10011, 00111, 01111, 11111, 11110, 11100, 11000, 10001, 00011, 00110, 01101, 11011, 10111, 01110, 11101, 11010, 10101, 01010, 10100, 01000, 10000, 00001, 00010, 00100, 01001, 10010, 00101, 01011, 10110.
Получили 31 комбинацию, среди которых ни одна не повторяется. Следовательно свойство окна выполняется.
Автокорреляционная функция (АКФ):


Проверили полученные в результате расчётов значения с помощью программы (рис.2).

Рисунок 2 – Проверка с помощью программы
Проведем моделирование работы формирователя случайной гаммы. Для этого подсоединим к линейному рекуррентному регистру набор нелинейный элементов в соответствии с вариантом и заданием. Схема формирователя представлена на рисунке 3.

Рисунок 3 – Схема формирователя
Таблица моделирования:
№ |
Состояние ЛРР |
Результат узла 1 (И) |
Результат узла 2 (ИЛИ-НЕ) |
Результат узла 3 (УЛ) |
1 |
01100 |
0 |
1 |
1 |
2 |
10110 |
0 |
0 |
1 |
3 |
01011 |
0 |
0 |
0 |
4 |
00101 |
0 |
0 |
1 |
5 |
10010 |
0 |
0 |
0 |
6 |
01001 |
0 |
0 |
0 |
7 |
00100 |
0 |
1 |
1 |
8 |
00010 |
0 |
0 |
0 |
9 |
00001 |
0 |
0 |
0 |
10 |
10000 |
0 |
1 |
1 |
11 |
01000 |
0 |
1 |
1 |
12 |
10100 |
0 |
1 |
1 |
13 |
01010 |
0 |
0 |
0 |
14 |
10101 |
0 |
0 |
1 |
15 |
11010 |
1 |
0 |
0 |
16 |
11101 |
1 |
0 |
0 |
17 |
01110 |
0 |
0 |
1 |
18 |
10111 |
0 |
0 |
1 |
19 |
11011 |
1 |
0 |
0 |
20 |
01101 |
0 |
0 |
1 |
21 |
00110 |
0 |
0 |
1 |
22 |
00011 |
0 |
0 |
0 |
23 |
10001 |
0 |
0 |
0 |
24 |
11000 |
1 |
1 |
0 |
25 |
11100 |
1 |
1 |
1 |
26 |
11110 |
1 |
0 |
0 |
27 |
11111 |
1 |
0 |
0 |
28 |
01111 |
0 |
0 |
1 |
29 |
00111 |
0 |
0 |
1 |
30 |
10011 |
0 |
0 |
0 |
31 |
11001 |
1 |
0 |
0 |
Получили следующие последовательности:
ЛРП: 0110011111000110111010100001001
Узел 1: 1000111100001001100000000000000
Узел 2: 0000001100000000000111001000001
Узел 3: 0011001000110110010111001001011
Исследуем полученную последовательность на выходе формирователя гаммы:
Последовательность: 0011001000110110010111001001011
Период последовательности: 31
Баланс единиц и нулей: 15 единиц, 16 нулей. Свойство баланса выполняется.
Серии: 7(1), 9(2), 2(3), 0(4), 0(5). Свойство серий не выполняется.
Свойство «окна»:
 – выходная
последовательность.
– выходная
последовательность.
Окна длиной 5: 00110, 01100, 11001, 10010, 00100, 01000, 10001, 00011, 00110, 01101, 11011, 10110, 01100, 11001, 10010, 00101, 01011, 10111, 01110, 11100, 11001, 10010, 00100, 01001, 10010, 00101, 01011, 10110, 01100, 11001, 10011.
Получили 31 комбинацию, среди которых не повторяются только 10, следовательно, свойство «окна» не выполняется.
Получили многочлен для характеристического уравнения (рис.4).
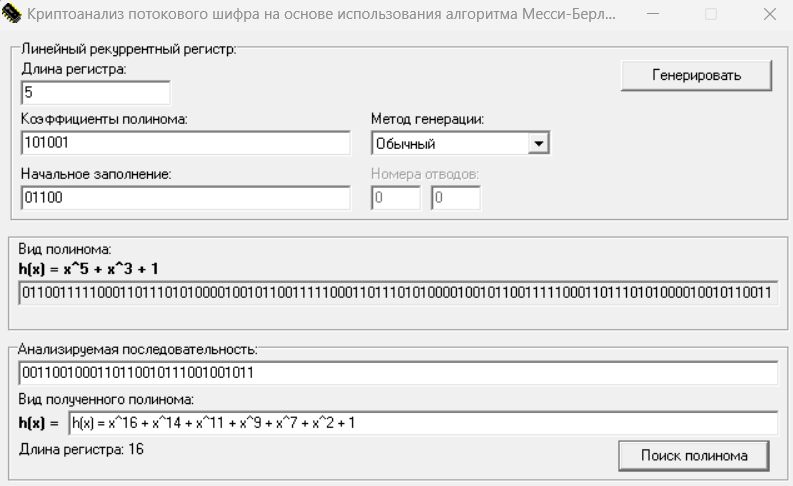
Рисунок 4 – Вид полученного полинома
Получили:

Эквивалентный линейный рекуррентный регистр представлен на рисунке 5.

Рисунок 5 – Эквивалентный ЛРР
Сформированная шифрующая гамма непригодна для шифрования сообщений, т.к. не выполняется свойство серии и свойство окна.
Так как длина эквивалентного ЛРР составляет 16, отсюда следует что, линейная эквивалентная сложность равна 16.
Вывод: В ходе выполнения лабораторной успешно провели анализ работы формирователя случайной гаммы и исследовали характеристики гаммы. Шифрующая гамма – это последовательность псевдослучайных, выработанных по специальному алгоритму, символов, которая используется для шифрования данных в криптографии. Метод гаммирования становиться бессильным, если злоумышленнику становится известен фрагмент исходного текста и соответствующая ему шифрограмма. Одним из методов криптоанализа является использование алгоритма Берлекэмпа-Месси, позволяющий найти длину эквивалентного ЛРР, начальное заполнение и как следствие – вычислить продолжение гаммы.
Санкт-Петербург 2023 г

