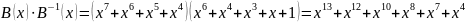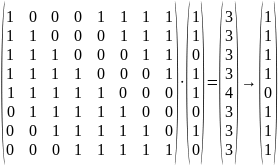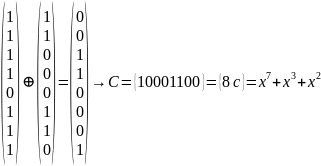Лабораторная работа №9

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА» (СПбГУТ)

Факультет Инфокоммуникационных сетей и систем Кафедра Защищенных систем связи

Дисциплина Криптографические методы защиты информации

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №9

Изучение и исследование блокового шифра AES

(тема отчета)

Информационная безопасность (10.03.01)

(код и наименование направления/специальности)

Студент группы ИКБ-06:

Ерохин А.Г.

(Ф.И.О.) (подпись)

Д.т.н., проф. каф. ЗСС:

Яковлев В.А.

(Ф.И.О.) (подпись)

Цель работы: Изучить преобразования, выполняемые при шифровании и дешифровании сообщений в блоковом шифре AES, а также исследовать некоторые его свойства.

Используемое программное обеспечение: Для работы используется специальная программа “Rijndael”

Задание:

1. Для случайно генерируемых сообщений и ключей просмотреть все операции, выполняемые в 10 раундах шифра, а также метод формирования раундовых ключей;

2. Просмотреть структуру основных раундовых операций (формирование обратных элементов, умножение на матрицы, циклические сдвиги, сложение с раундовым ключом.);

3. Исследовать некоторые свойства шифра: выбор “слабых” ключей, размножение ошибок при шифровании и дешифровании;

4. Проверить “вручную” правильность вычисления обратных элементов и умножение на матрицы в конечных полях, выполняемых шифром;

5. Найти оценку коэффициента лавинного эффекта для каждого раунда.

Ход выполнения лабораторной работы:

Создаем случайный блок данных и случайный текущий ключ (рис.1).

Рисунок 1 – Генерация случайного ключа и блока данных

Выполнили процедуру шифрования, наблюдая последовательность выполняемых преобразований на каждом раунде, включая и преобразования раундовых ключей (для примера рассмотрим несколько раундов):

Раунд 0:

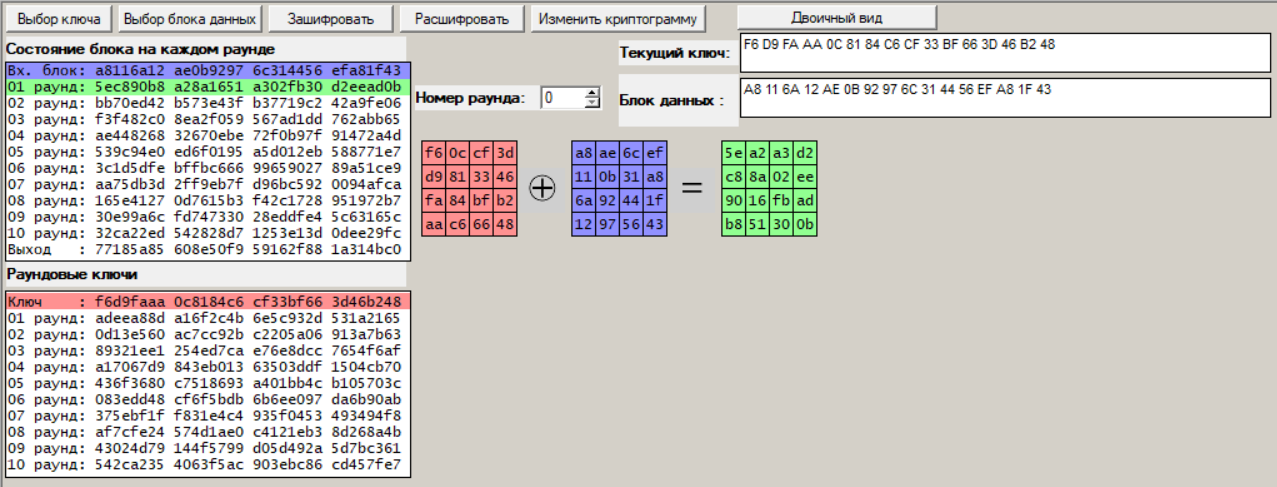
Рисунок 2 – Процедура шифрования, раунд 0

Раунд 1:

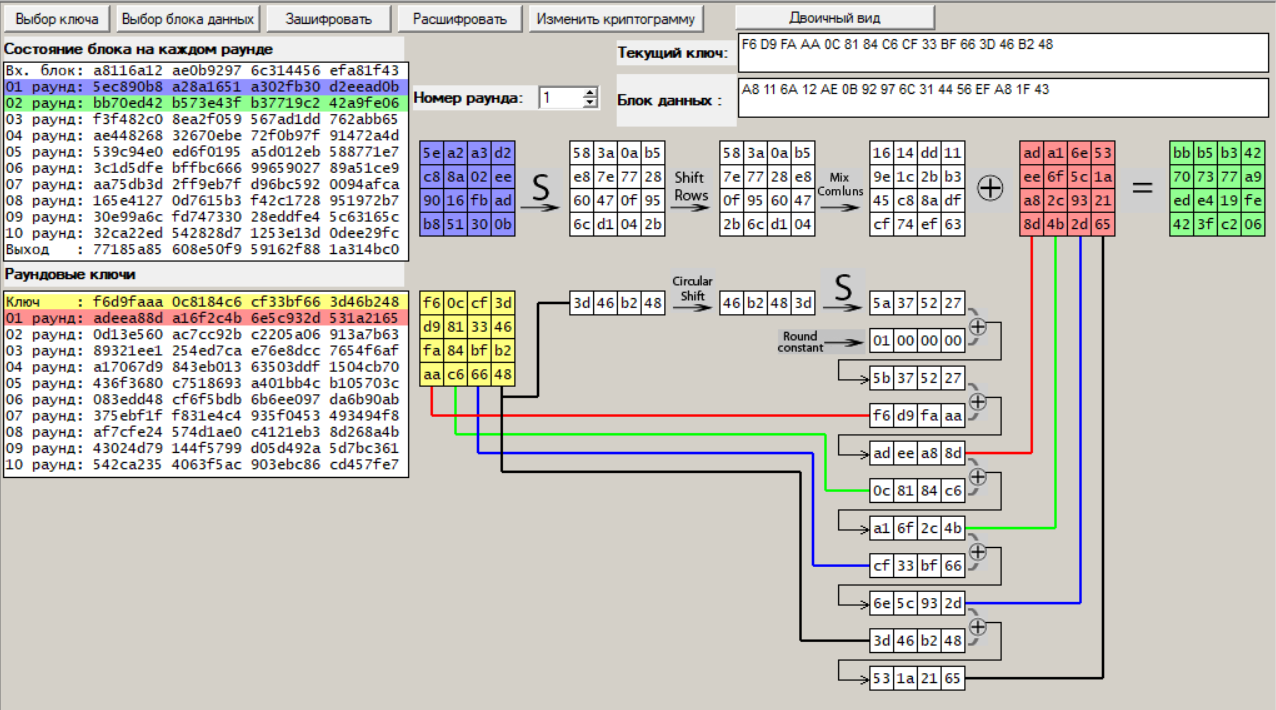
Рисунок 3 – Процедура шифрования, раунд 1

Раунд 2:

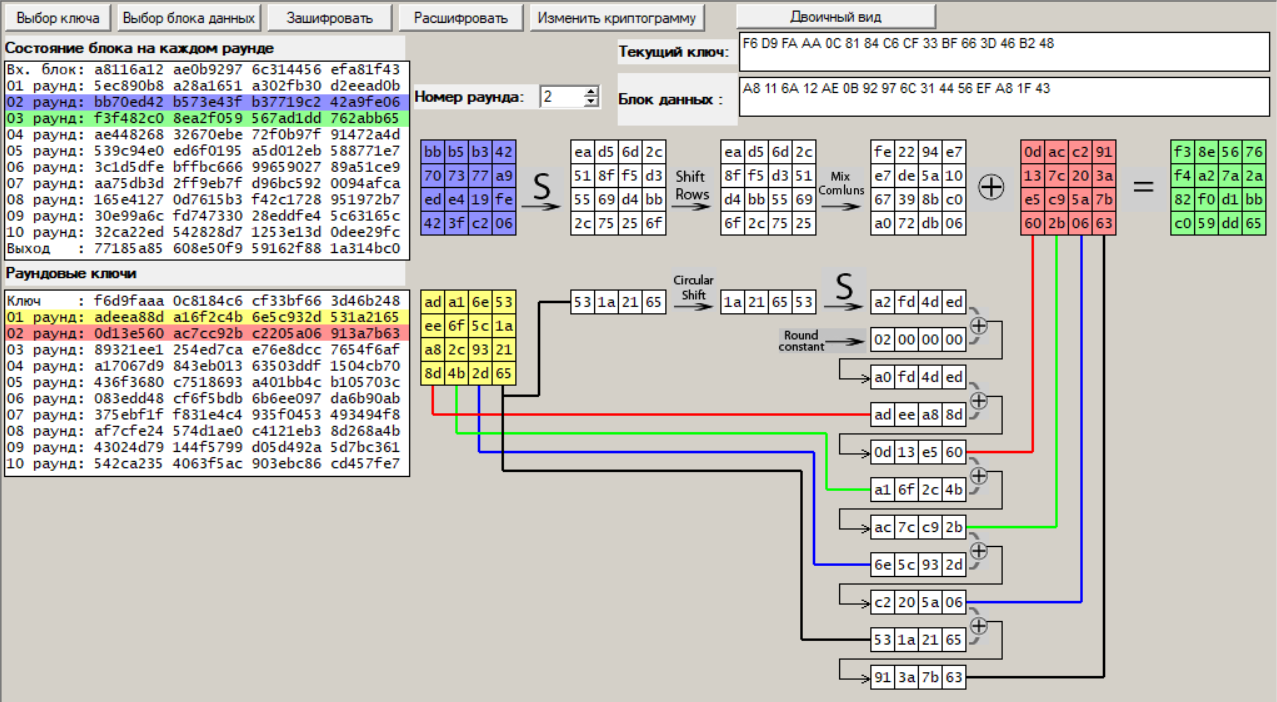
Рисунок 4 – Процедура шифрования, раунд 2

Раунд 8:

Рисунок 5 – Процедура шифрования, раунд 8

Выполнили процедуру дешифрования, наблюдая последовательные преобразования криптограммы в открытое сообщение, убеждаемся в обратном порядке формирования раундовых ключей (для примера рассмотрим несколько раундов):

Раунд 0:

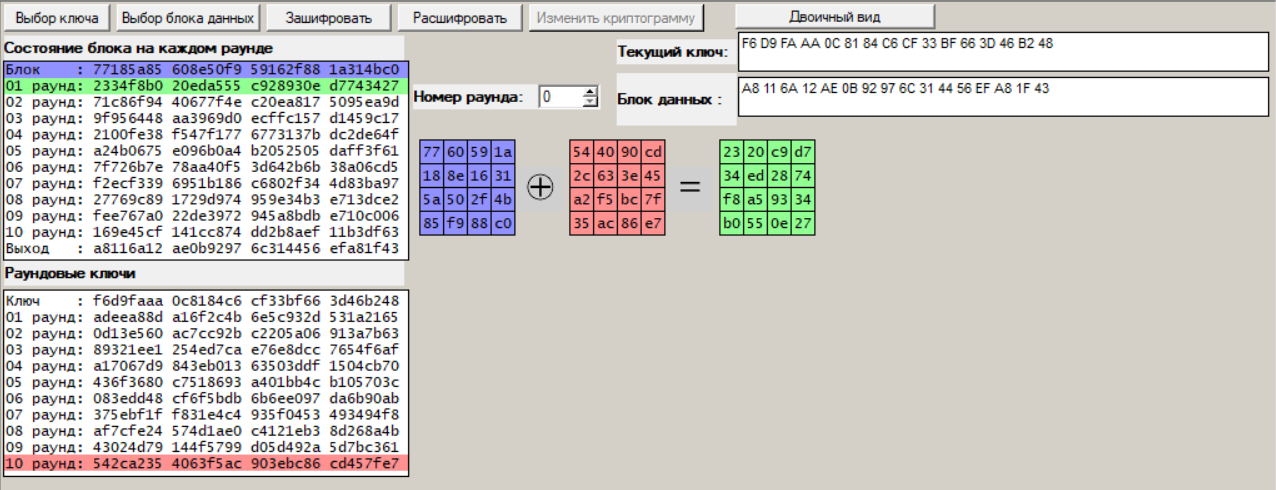
Рисунок 6 – Процедура дешифрования, раунд 0

Раунд 1:

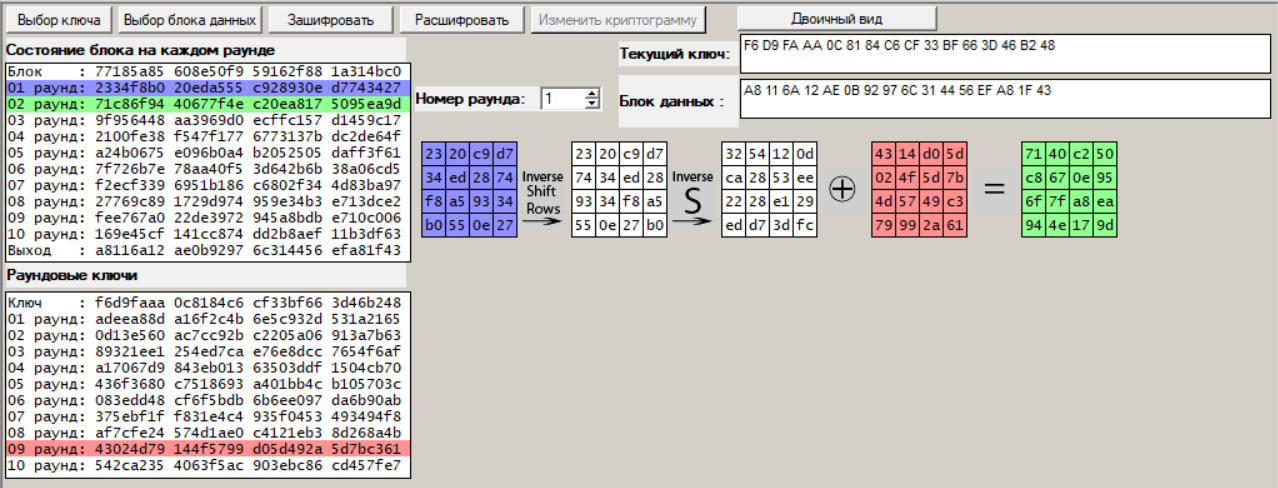
Рисунок 7 – Процедура дешифрования, раунд 1

Раунд 2:

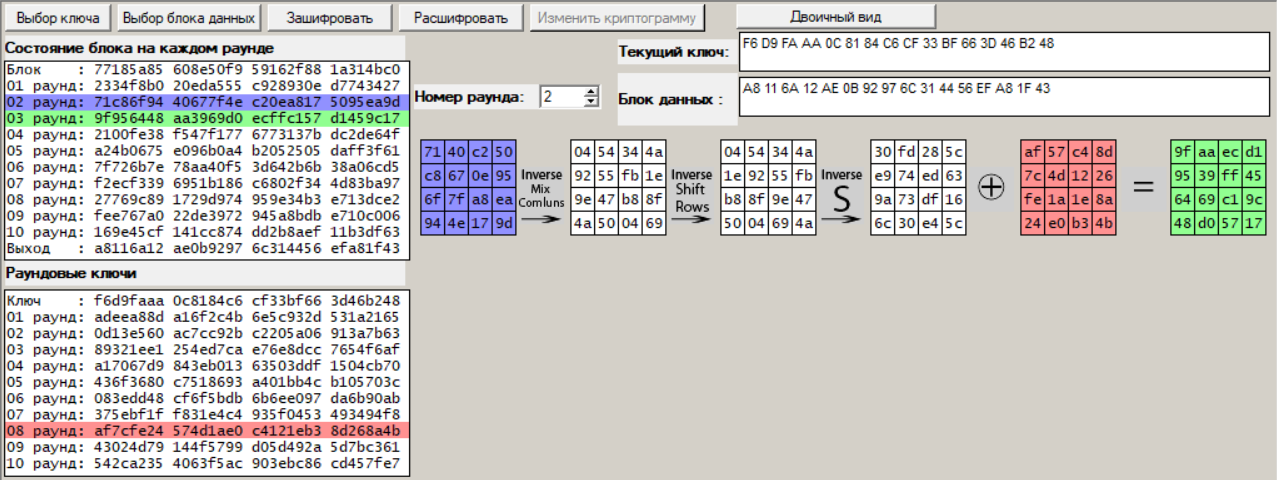
Рисунок 8 – Процедура дешифрования, раунд 2

Раунд 8:

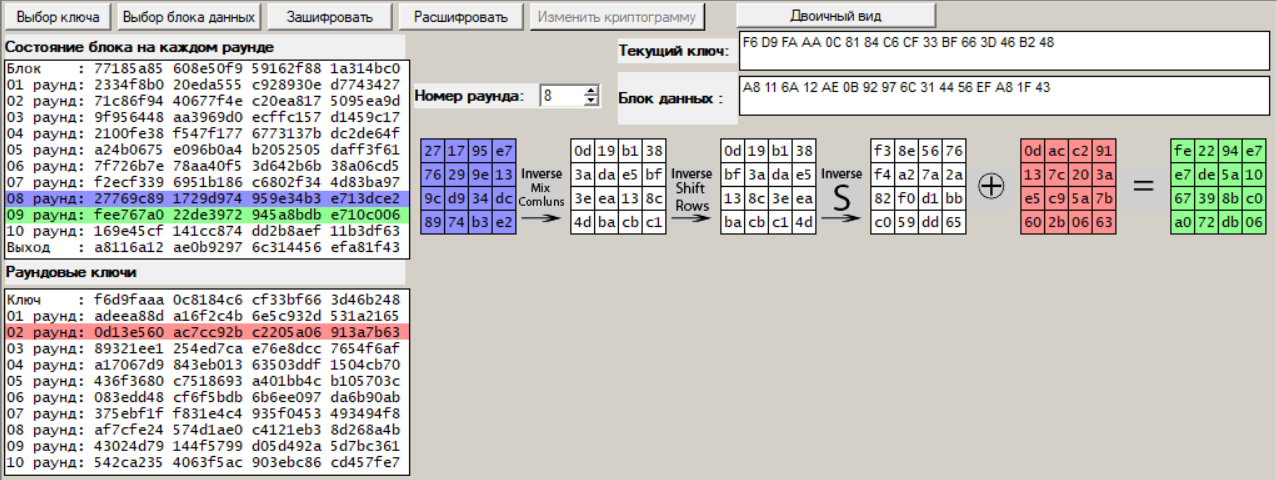
Рисунок 9 – Процедура дешифрования, раунд 8

Далее, выбрали один из раундов и изучили алгоритм формирования обратных элементов конечного поля и аффинно-линейное преобразование (рис.10).

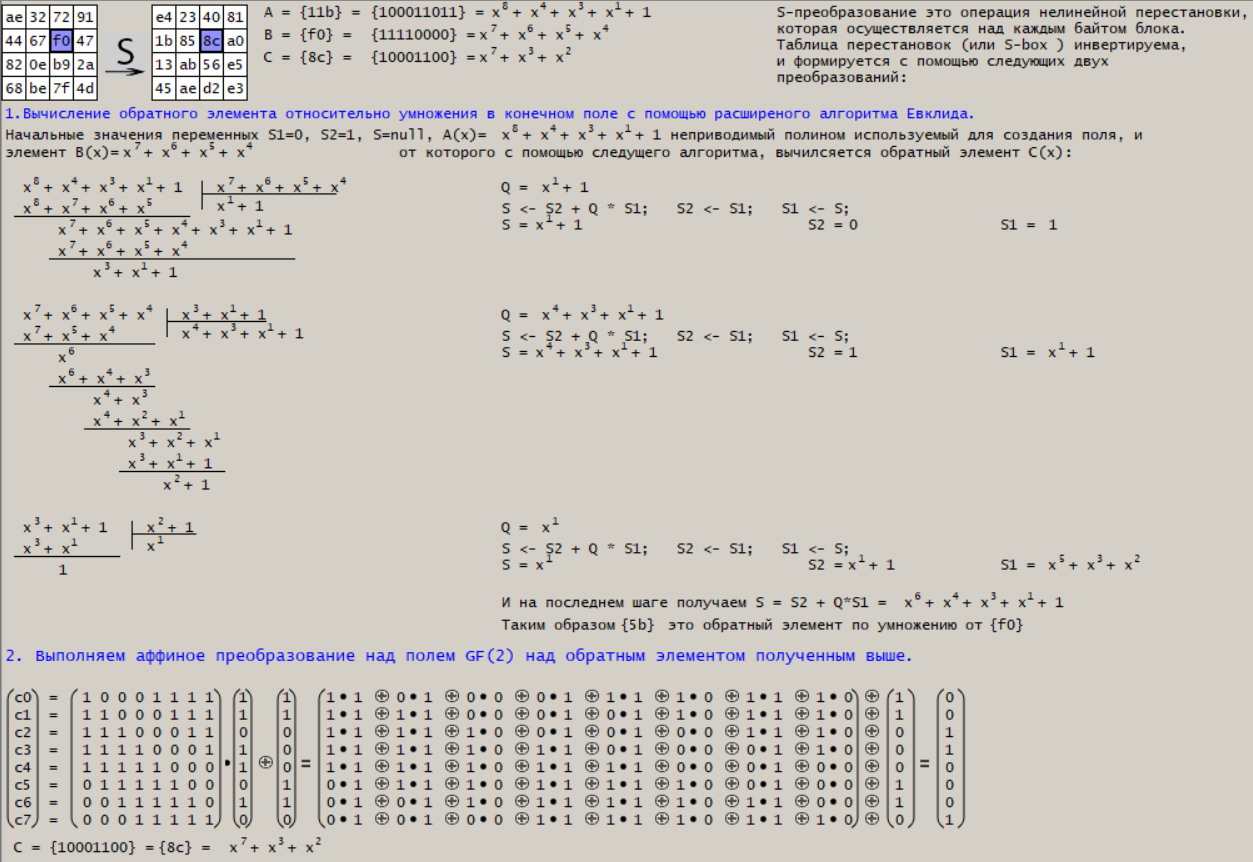
Рисунок 10 – Вычисление обратного элемента и аффинное преобразование

Проверили при помощи вычислений правильность нахождения обратного элемента в конечном поле GF(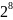 ) для заданного неприводимого полинома , образующего это поле:

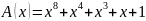
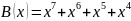
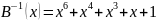
Докажем, что

1. 

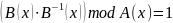
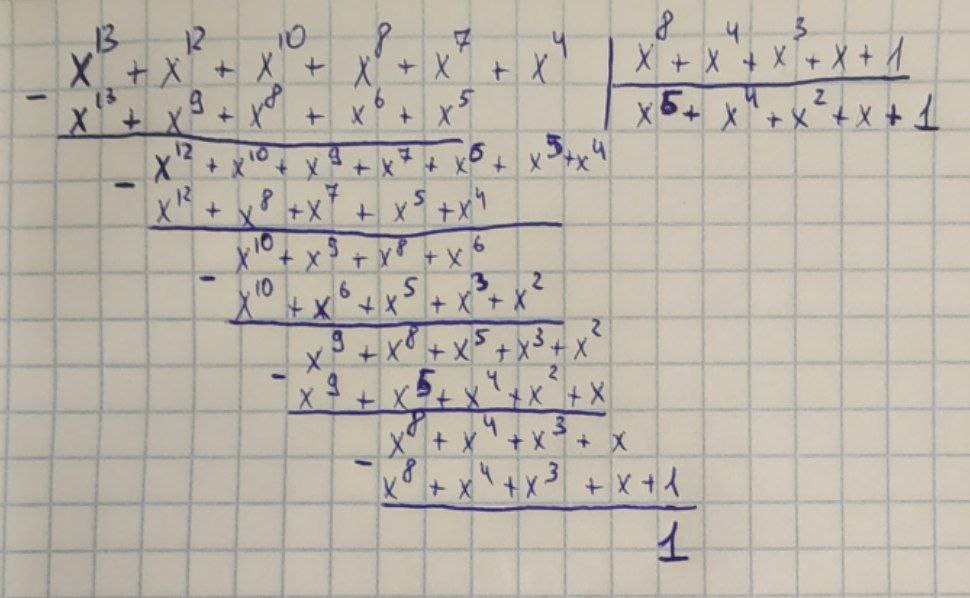
Так как остаток от деления получился равный 1, следовательно равенство верно, из чего получаем, что {5b} – обратный элемент по умножению от {f0}. Что и требовалось доказать.

Проверили правильность выполнения аффинно-линейного преобразования для выбранной клетки квадрата:

1. 

2. 

Результат ручного вычисления полностью совпал с результатом работы программы, следовательно аффинно-линейное преобразование выполнено правильно.

Далее проверили правильность выполнения операции “Shift Rows” (рис.11).

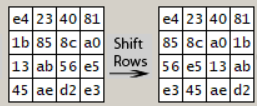
Рисунок 11 – Операция Shift Rows

Первая строка не имеет сдвига. Вторая строка сдвигается влево на 1. Третья строка сдвигается влево на 2, а четвертая – на 3. На рисунке 11 наглядно видны данные сдвиги, следовательно операция Shift Rows выполняется верно.

Следующим шагом изучили структуру операции “Mix Columns” (рис.12).

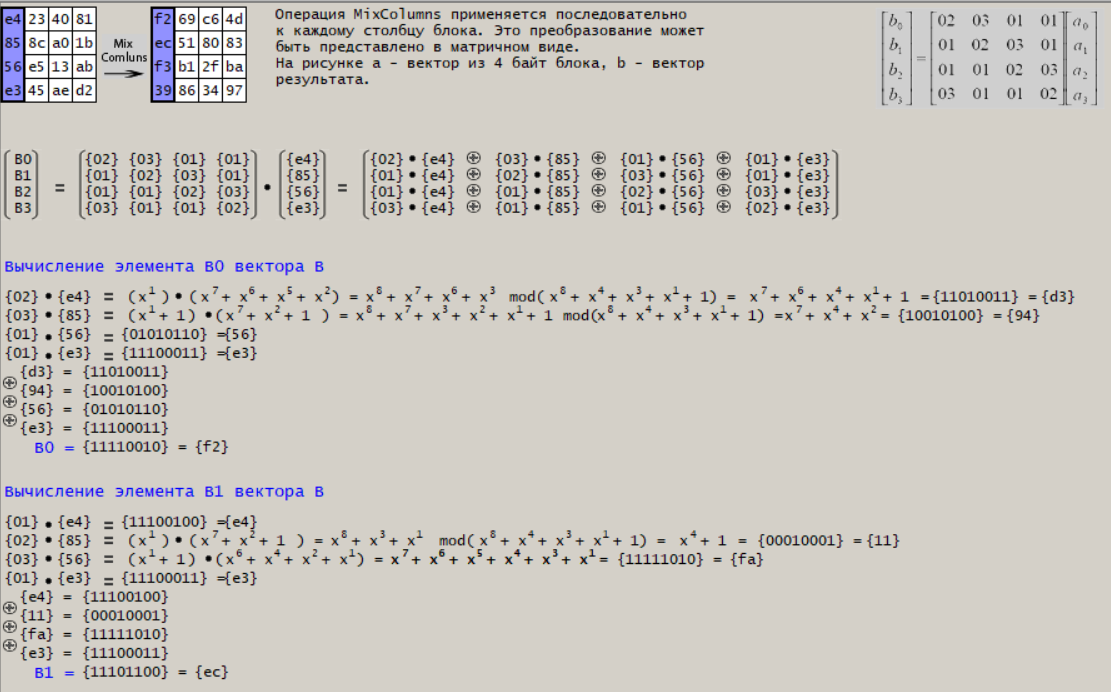
Рисунок 12 – Операция Mix Columns

В следующем этапе лабораторной работы установили ключ, состоящий из нулей, что привело к увеличению «случайности» ключей и промежуточных криптограмм при переходе от раунда к раунду (рис.13).

Рисунок 13 – Установка ключа, состоящего из нулей

Рассмотрим несколько первых раундов:

Раунд 1:

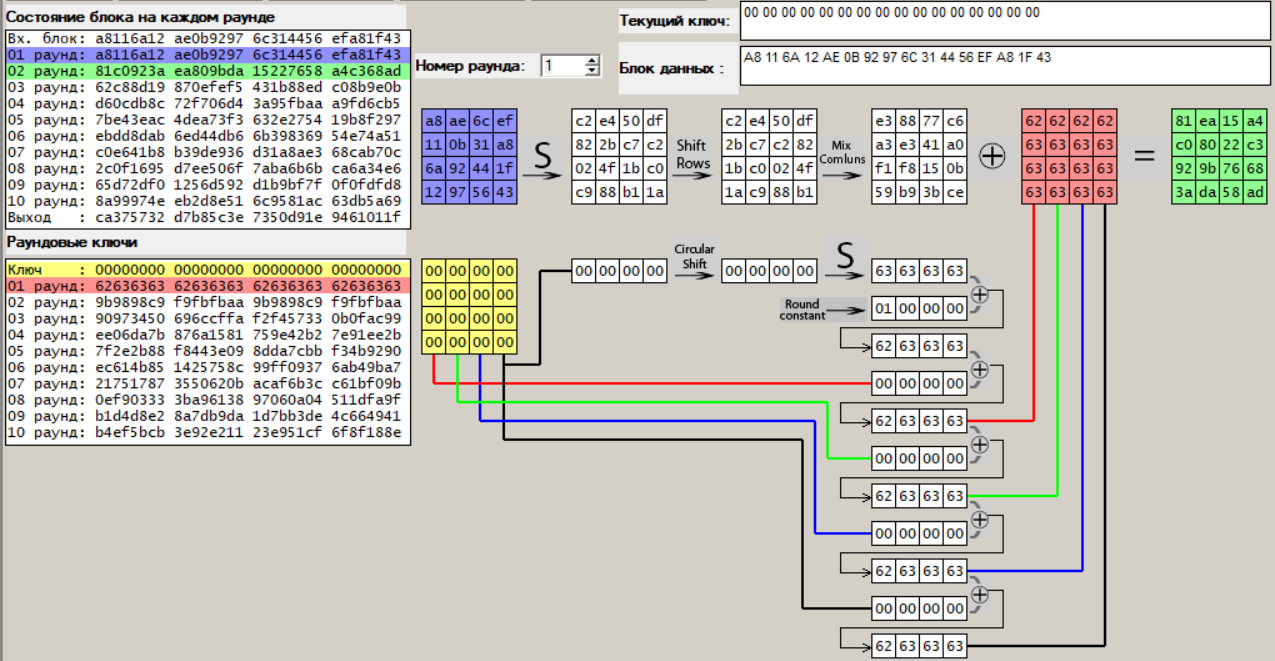
Рисунок 14 – Первый раунд шифрования

Раунд 2:

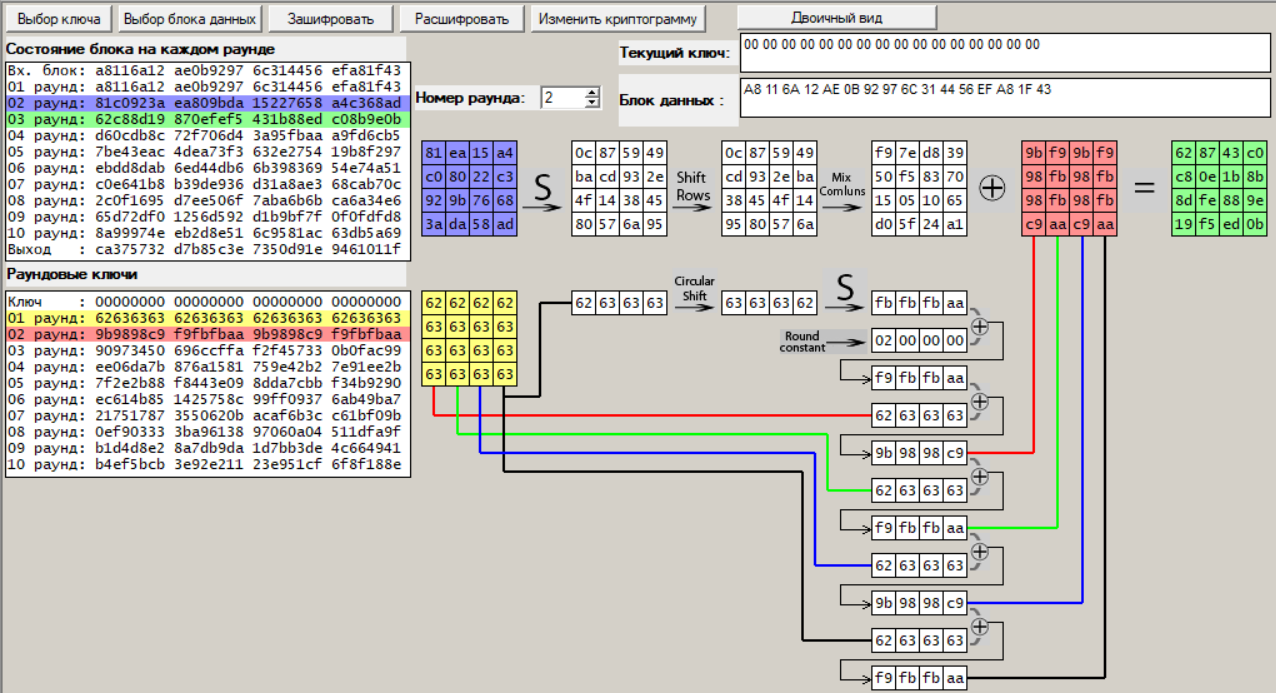
Рисунок 15 – Второй раунд шифрования

Раунд 3:

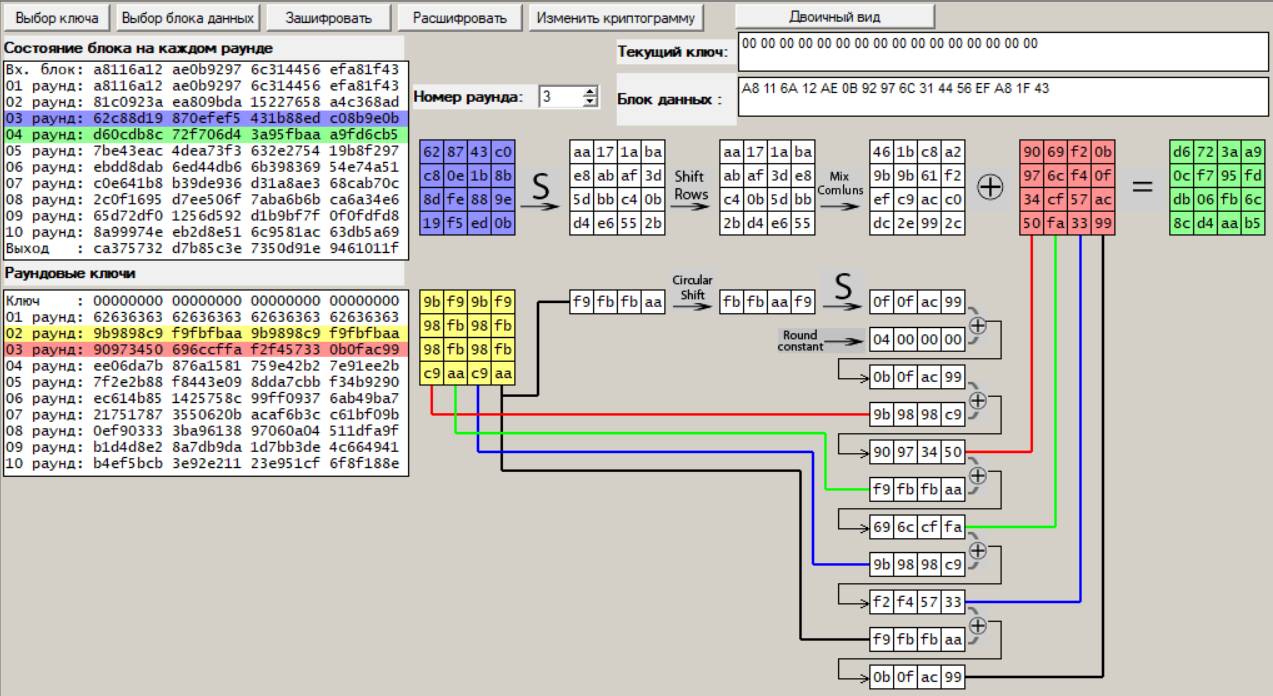
Рисунок 16 – Третий раунд шифрования

Видим, что при каждом последующем раунде, наблюдается увеличение «случайности» раундовых ключей и промежуточных криптограмм

Далее выбрали открытое сообщение, состоящее из всех нулей. При случайно сгенерированном ключе, наблюдали изменение раундовых криптограмм. В качестве примера взяли первые три раунда (рис.17 – 19).

Раунд 1:

Рисунок 17 – Первый раунд шифрования

Раунд 2:

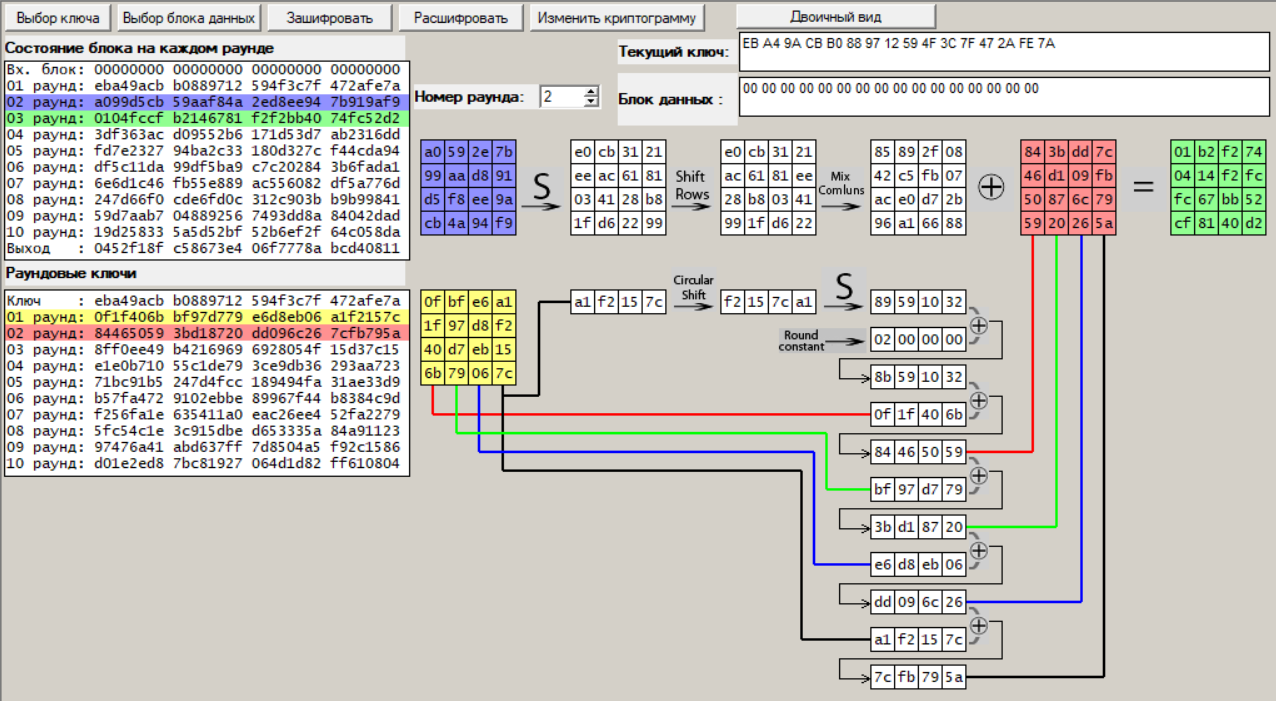
Рисунок 18 – Второй раунд шифрования

Раунд 3:

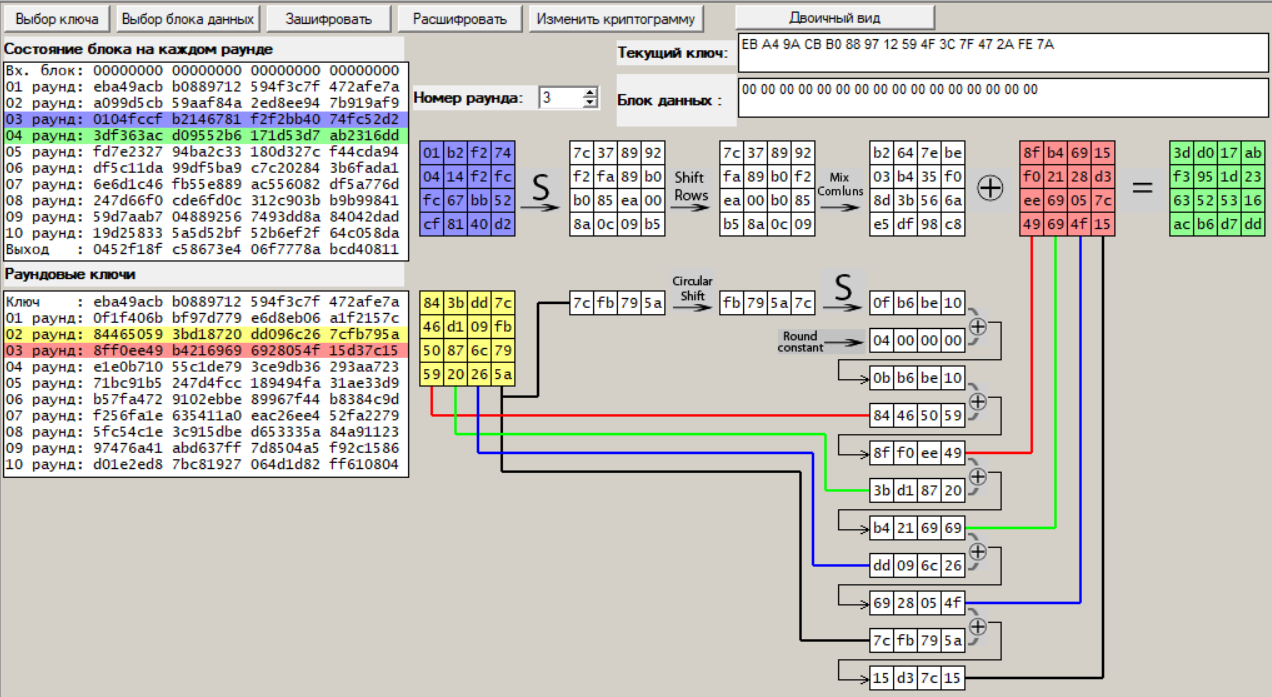
Рисунок 19 – Третий раунд шифрования

Следующим этапом необходимо выполнить аналогичные действия, внеся одну «1» в исходный блок данных. Место единицы в блоке определяется по формуле 4*N. Так как номер в списке – 10, следовательно место для единицы 4*10 = 40. В качестве примера взяли первые три раунда (рис.20 – 22).

Раунд 1:

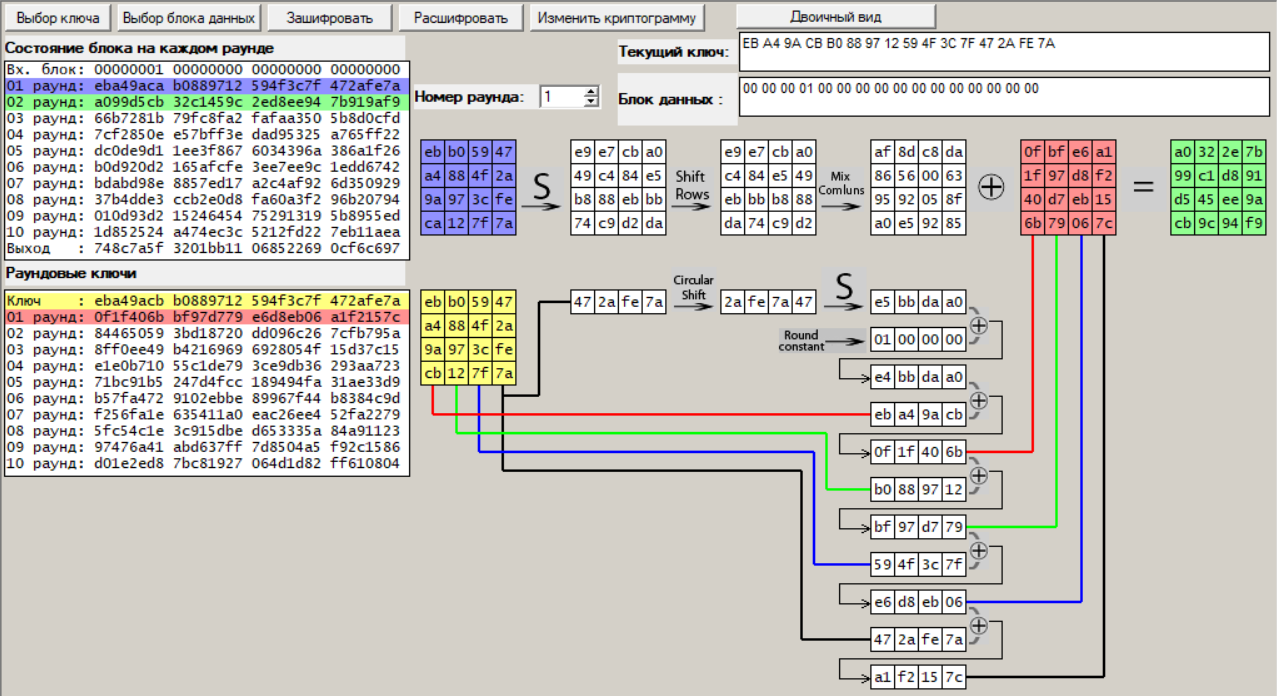
Рисунок 20 – Первый раунд шифрования

Раунд 2:

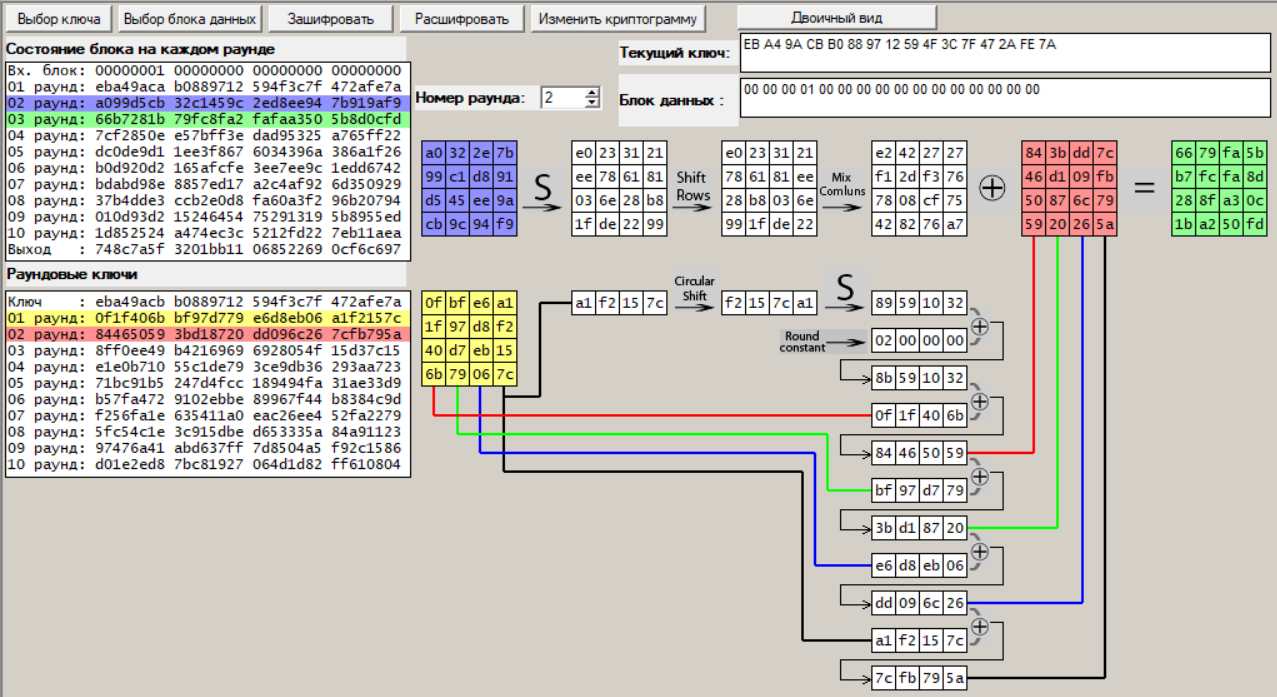
Рисунок 21 – Второй раунд шифрования

Раунд 3:

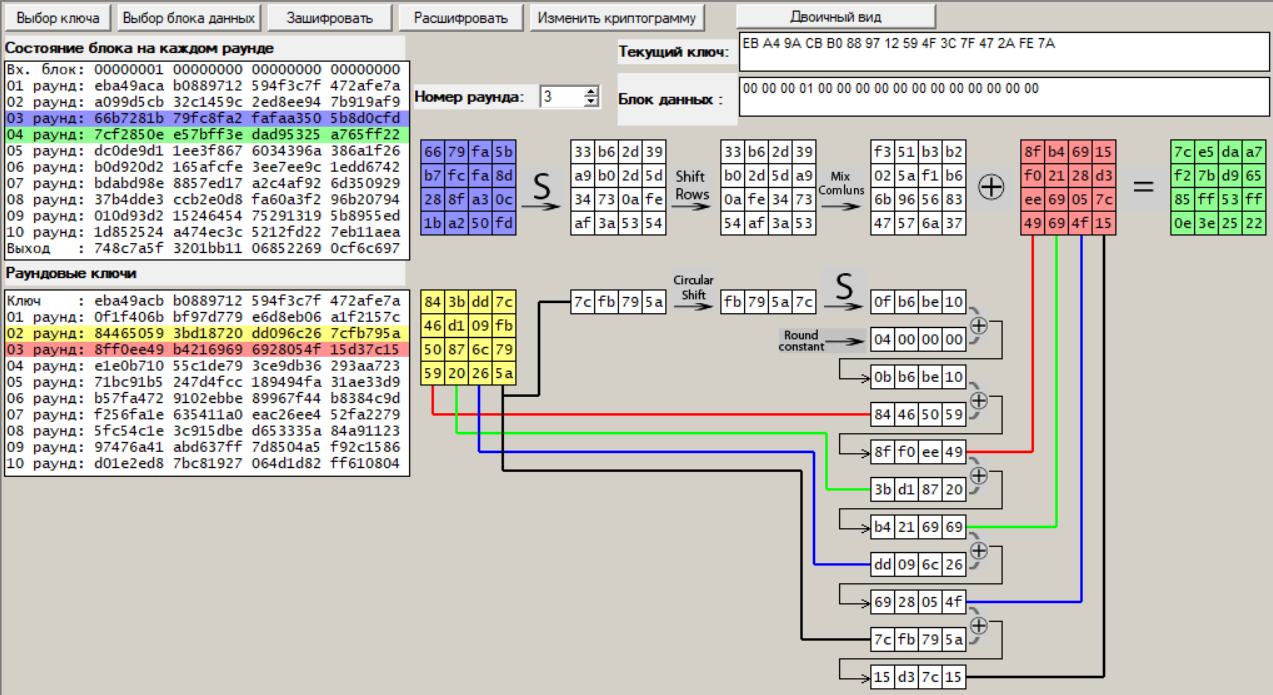
Рисунок 22 – Третий раунд шифрования

Сравнили по раундам промежуточные криптограммы при сообщении из всех нулей и сообщении из одной единицы и остальных нулей. Различающееся количество бит называется коэффициентом лавинного эффекта; найдем его (табл.1).

Таблица 1 – Коэффициент лавинного эффекта

Раунд	без/с “1”	Промежуточная криптограмма	Кол-во разных бит	Коэфф-нт лавинного эффекта
1	без “1”	eba49acb b0889712 594f3c7f 472afe7a	1	7,8%
	с “1”	eba49aca b0889712 594f3c7f 472afe7a
2	без “1”	a099d5cb 59aaf84a 2ed8ee94 7b919af9	21	16,4%
	с “1”	a099d5cb 32c1459c 2ed8ee94 7b919af9
3	без “1”	0104fccf b2146781 f2f2bb40 74fc52d2	56	43,8%
	с “1”	66b7281b 79fc8fa2 fafaa350 5b8d0cfd
4	без “1”	3df363ac d09552b6 171d53d7 ab2316dd	58	45,3%
	с “1”	7cf2850e e57bff3e dad95325 a765ff22
5	без “1”	fd7e2327 94ba2c33 180d327c f44cda94	60	46,9%
	с “1”	dc0de9d1 1ee3f867 6034396a 386a1f26
6	без “1”	df5c11da 99df5ba9 c7c20284 3b6fada1	63	49,2%
	с “1”	b0d920d2 165afcfe 3ee7ee9c 1edd6742
7	без “1”	6e6d1c46 fb55e889 ac556082 df5a776d	60	46,9%
	с “1”	bdabd98e 8857ed17 a2c4af92 6d350929
8	без “1”	247d66f0 cde6fd0c 312c903b b9b99841	63	49,2%
	с “1”	37b4dde3 ccb2e0d8 fa60a3f2 96b20794
9	без “1”	59d7aab7 04889256 7493dd8a 84042dad	60	46,9%
	с “1”	010d93d2 15246454 75291319 5b8955ed
10	без “1”	19d25833 5a5d52bf 52b6ef2f 64c058da	54	42,2%
	с “1”	1d852524 a474ec3c 5212fd22 7eb11aea

По полученным данным в таблице 1 построим график зависимости коэффициента лавинного эффекта.

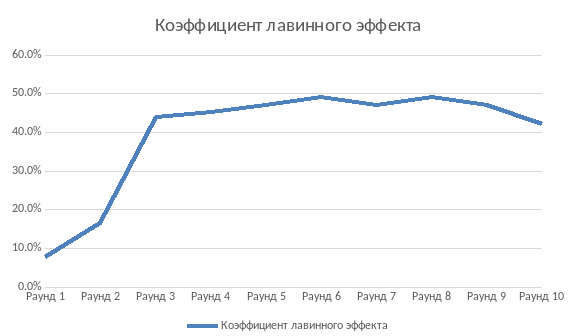
Вывод: В ходе выполнения лабораторной работы изучили преобразования, выполняемые при шифровании и дешифровании сообщений в блоковом шифре AES. В ходе работы успешно вычислили обратный элемент и аффинное преобразование, изучили структуру операции Mix Columns. В заключительной части работы наглядно продемонстрировали лавинный эффект, путём сравнения промежуточных криптограмм, полученных при исходном блоке данных со всеми нулями и блоке данных с одной «1» и остальными нулями. Если криптографический алгоритм не обладает лавинным эффектом в достаточной степени, криптоаналитик может сделать предположение о входной информации, основываясь на выходной информации. На графике видно, что уже на третьем раунде коэффициент лавинного эффекта близок к 0,5, что означает хорошее выполнение лавинного критерия.

Санкт-Петербург 2023 г