Лабораторная работа №3

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА» (СПбГУТ)

Факультет Инфокоммуникационных сетей и систем Кафедра Защищенных систем связи

Дисциплина Криптографические методы защиты информации

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №3

Анализ системы шифрования по её графовой модели

(тема отчета)

Информационная безопасность (10.03.01)

(код и наименование направления/специальности)

Студент группы ИКБ-06:

Ерохин А.Г.

(Ф.И.О.) (подпись)

Д.т.н., проф. каф. ЗСС:

Яковлев В.А.

(Ф.И.О.) (подпись)

Цель работы: Научиться оценивать стойкость системы шифрования по графовой модели.

Задание:

1. Выбрать вариант задания (табл.), соответствующий Вашему номеру по журналу.

2. Расставить ключи, так чтобы обеспечить единственность шифрования-дешифрования.

3. Найти вероятности всех криптограмм P(E_i);

4. Найти апостериорные вероятности всех сообщений P(M_i/E_j);

5. Сравнить априорные и апостериорные вероятности. Сделать вывод является ли исследуемая система безусловно стойкой (идеальной.

6. На основании теорем о достаточных и необходимых условиях существования идеальной системы сделать вывод о стойкости шифрования.

Ход выполнения лабораторной работы:

Для выполнения лабораторной работы необходимо выбрать задание по варианту, согласно номеру в списке группы – вариант 10. Исходные данные представлены в таблице 1.

Таблица 1 – Исходные данные

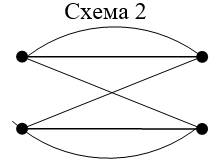
№ вар	Априорные вероятности сообщений			Вероятности ключей			Граф системы шифрования
	P(M1)	P(M2)	P(M3)	P(K1)	P(K2)	P(K3)
10	равновероятны		-	0.45	0.25	0.3

На представленном графе системы шифрования необходимо указать положение сообщений, ключей и криптограмм, для обеспечения единственности шифрования-дешифрования (рис.1)

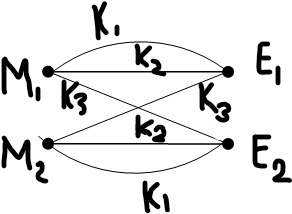
Рисунок 1 – Расстановка ключей

Следующим этапом выполнения работы является нахождение вероятностей всех криптограмм P(E_i). Вероятность криптограммы находится по формуле:

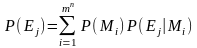, где 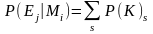- сумма вероятностей ключей, связывающих i-е сообщение и j-ю криптограмму.

Так как по условию априорные вероятности сообщени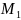й и 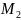– равновероятны, следовательно .

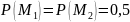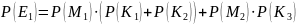
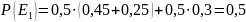
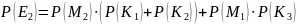
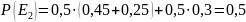
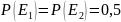
Далее необходимо найти апостериорные вероятности всех сообщений P(M_i/E_j). Апостериорная вероятность сообщения находится по формуле:

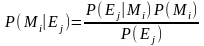
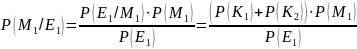
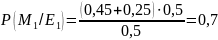
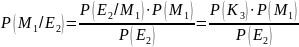
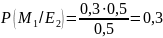
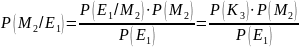
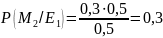
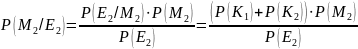
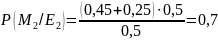
Сравнили априорные и апостериорные вероятности.

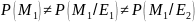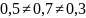
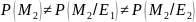т.к.

т.к.

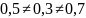
Вывод: В ходе выполнения лабораторной работы провели анализ системы шифрования по её графовой модели. Из полученных расчётов получили, что априорные и апостериорные вероятности не равны, следовательно представленная система шифрования не является безусловно стойкой. К такому заключению можно было прийти без проведения расчётов. Количество ключей не меньше числа сообщений, то необходимое условие существования ИКС выполняется.

Санкт-Петербург 2023 г