Лабораторная работа №11

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА» (СПбГУТ)

Факультет Инфокоммуникационных сетей и систем Кафедра Защищенных систем связи

Дисциплина Криптографические протоколы

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №11

Криптографические протоколы проверяемого разделения секрета

(тема отчета)

Информационная безопасность (10.03.01)

(код и наименование направления/специальности)

Студент группы ИКБ-06:

Ерохин А.Г.

(Ф.И.О.) (подпись)

Д.т.н., проф. каф. ЗСС:

Яковлев В.А.

(Ф.И.О.) (подпись)

Цель работы:

Закрепление теоретических знаний студентов по криптографическим протоколам разделения секрета и изучения схем проверяемого разделения секрета Фельдмана и Педерсена.

Ход работы:

Лабораторная работа выполняется согласно варианту 11. Исходные данные представлены в таблице 1.

Таблица 1 – Исходные данные

Номер варианта	Параметры		Секрет
11	3, 4	131, 13	9	99

Часть 1. Исследование схемы проверяемого разделения секрета Фельдмана

1. Необходимо реализовать схему разделения секрета. В данном режиме во вкладке «Разделение секрета» вводим значения и в блоке «Пороговая схема» (рис.1).

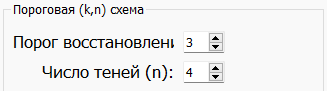
Рисунок 1 – Схема разделения секрета

2. Инициализация протокола

Выбраны .

Проверим выполнение условия :

Можно сделать вывод, что условие выполняется.

Необходимо выбрать , где :

Пусть , тогда

Пусть

Введём указанные значения в блок «Исходные данные» (рис.2).

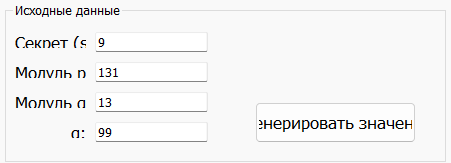
Рисунок 2 – Исходные данные

3. Разделение секрета

Выбирается многочлен с коэффициентами . Для этого сгенерируем многочлен в программе (рис.3).

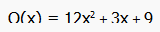
Рисунок 3 – Сгенерированный полином

, где

Вычисляются проверочные значения:

Проверим вычисленные значения с помощью программы (рис.4).

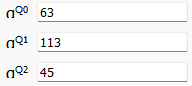
Рисунок 4 – Проверка вычисленных проверочных значений

Частные ключи (тени) вычисляются по формуле:

, где :

Проверим вычисленные значения теней с помощью программы (рис.5).

Рисунок 5 – Вычисленные тени

4. Проверка долей

Проверочное уравнение имеет вид:

.

Пусть второй участник решил проверить свою долю:

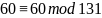
Проверка прошла успешно. Проверим правильность выполнения с помощью программы (рис.6).

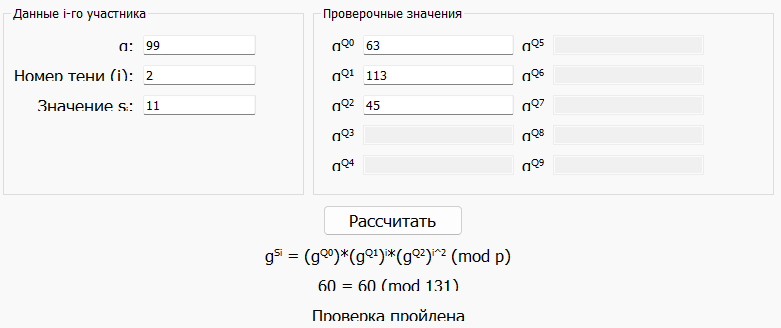
Рисунок 6 – Проверка долей

5. Восстановление секрета

Восстановим секрет для 1, 2 и 3 участников:

Полученное значение совпадает с заданным, следовательно секрет восстановлен верно. Проверим правильность с помощью программы (рис.7).

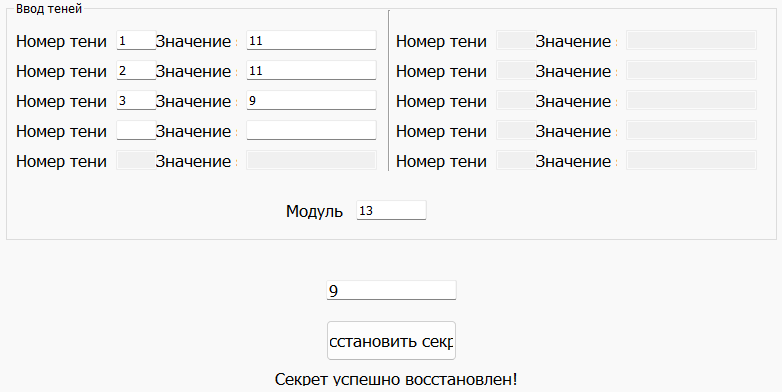
Рисунок 7 – Восстановление секрета

Часть 2. Исследование схемы проверяемого разделения секрета Педерсена

1. Необходимо реализовать схему разделения секрета. В данном режиме во вкладке «Разделение секрета» вводим значения и в блоке «Пороговая схема» (рис.8).

Рисунок 8 – Схема разделения секрета

2. Инициализация протокола

Выбраны .

Проверим выполнение условия :

Можно сделать вывод, что условие выполняется.

Необходимо выбрать , где :

Пусть , тогда

Пусть

Пусть , тогда

Введём указанные значения в блок «Исходные данные» (рис.9).

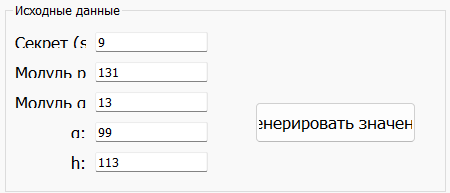
Рисунок 9 – Исходные данные

3. Разделение секрета

Выбираются два многочлена , степени 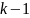над полем с коэффициентами и случайными коэффициентами и соответственно. Для этого необходимо сгенерировать многочлены в программе (рис.10).

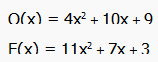
Рисунок 10 – Многочлены

, где

, где

Вычисляются проверочные значения, которые будут раздаваться всем участникам разделения:

Проверим проверочные значения с помощью программы (рис.11).

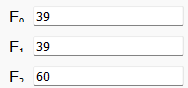
Рисунок 11 – Проверка вычисленных значений

Частные ключи (тени) вычисляются по формуле

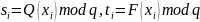, где :

Проверим вычисленные значения теней с помощью программы (рис.12).

Рисунок 12 – Вычисление теней

4. Проверка долей

Проверочное уравнение имеет вид:

Пусть второй участник решил проверить свою долю:

Проверка прошла успешно. Проверим правильность выполнения с помощью программы (рис.13).

Рисунок 13 – Проверка долей

5. Восстановление секрета

Восстановим секрет для 1, 2 и 3 участников:

Полученное значение совпадает с заданным, следовательно секрет восстановлен верно. Проверим правильность с помощью программы (рис.14).

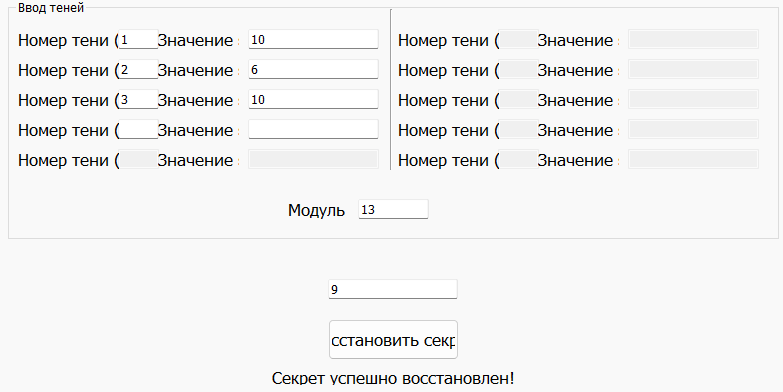
Рисунок 14 – Восстановление секрета

Вывод

В ходе выполнения лабораторной работы исследовали схемы проверяемого разделения секрета Фельдмана и Педерсена. С помощью заданных параметров и сгенерированных многочленов удалось разделить секрет, а также проверить долю одного из участников схемы. В заключительной части удалось успешно восстановить секрет в каждой из схем.

Санкт-Петербург 2023 г