Лабораторная работа №9

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА» (СПбГУТ)

Факультет Инфокоммуникационных сетей и систем Кафедра Защищенных систем связи

Дисциплина Криптографические протоколы

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №9

Изучение криптопротокола с разделением секретных данных между пользователями

(тема отчета)

Информационная безопасность (10.03.01)

(код и наименование направления/специальности)

Студент группы ИКБ-06:

Ерохин А.Г.

(Ф.И.О.) (подпись)

Д.т.н., проф. каф. ЗСС:

Яковлев В.А.

(Ф.И.О.) (подпись)

Цель работы:

Закрепить знания, полученные на лекциях дисциплине “Криптографические протоколы” по теме «протоколы разделения секрета».

Ход работы:

Часть 1. Моделирование схемы разделения секретов

Работа выполняется согласно варианту 11. Исходные данные представлены в табл.1.

Таблица 1 – Исходные данные

№ вар	Секрет k	a1	a2	p
11	15	1	6	21

Число теней

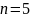
Порог восстановления

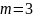
Секрет

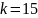
Полином:

Найдем тени k_i = h(x_i), где x_i = (1, 2, 3, 4, 5):

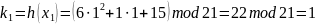
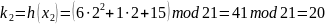
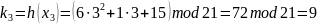
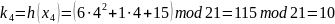
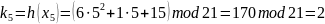
Используя тени 2, 3, 4 восстановим секрет .

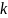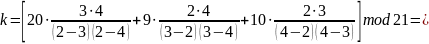
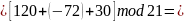[15 + 12 + 9] mod 21 = 15

Проверка:

Секрет восстановлен верно.

Часть 2. Разделение сеансового ключа

1. Выберем произвольное сообщение и представим его в шестнадцатеричной кодировке (рис.1).

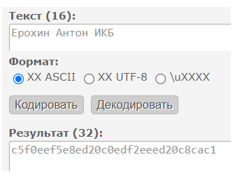
Рисунок 1 – Выбор сообщения

2. Запустим программу «AES.exe», сгенерируем случайный секрет (рис.2).

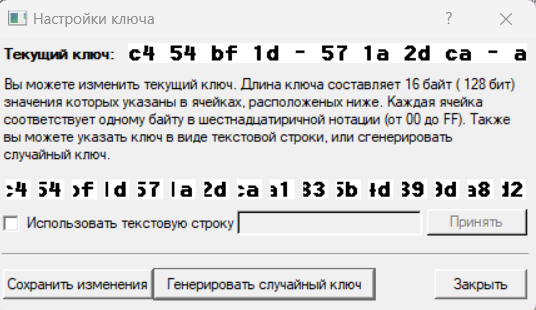
Рисунок 2 – Генерация ключа

Ключ: c454bf1d571a2dcaa1835b4d399da8d2

3. Заполнили блоки данных и произвели шифрование (рис.3 – 4).

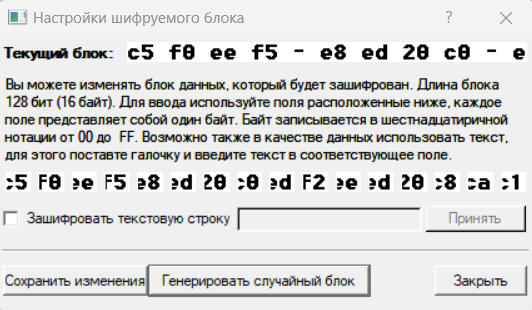
Рисунок 3 – Выбор исходного текстового файла

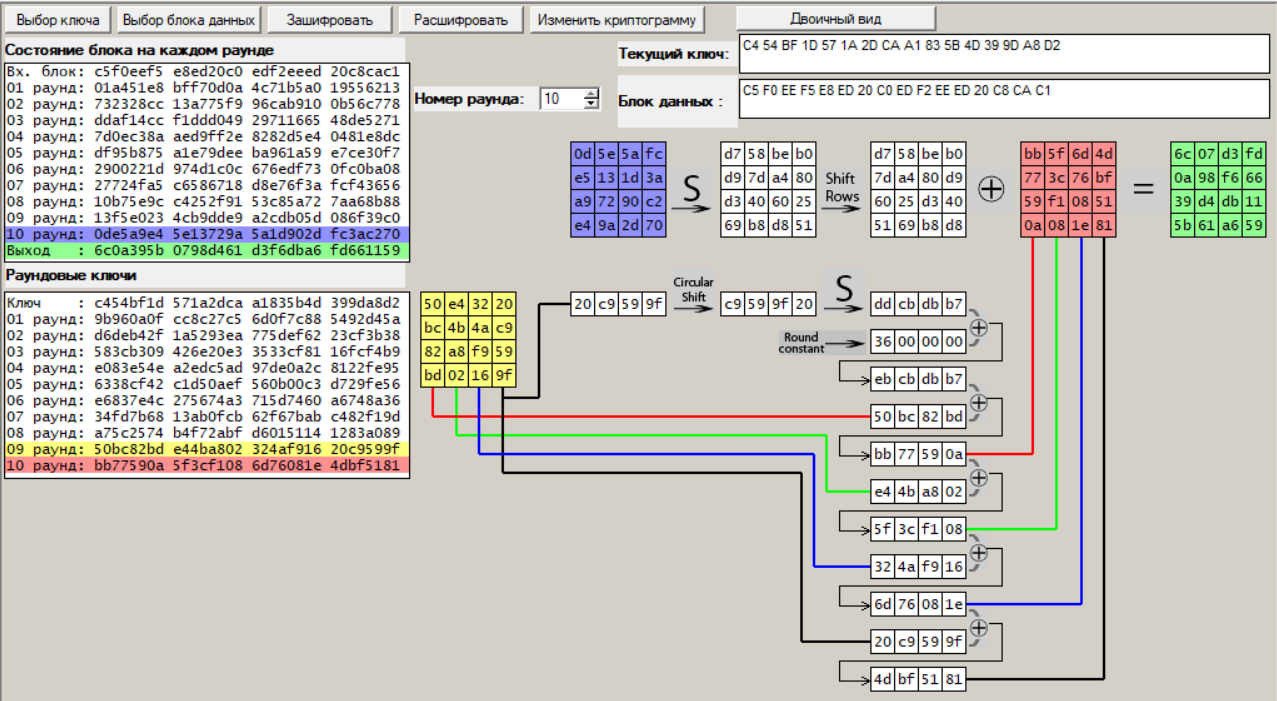
Рисунок 4 – Шифрование

4. Попробуем преобразовать криптограмму из шестнадцатеричного представления в текстовое (рис.5).

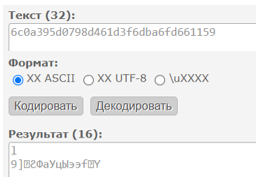
Рисунок 5 – Криптограмма

5. Так как разделение секретов производится в 10 системе счисления переведём полученный ключ в 10 систему счисления:

Ключ: 260968716374768291162798789254627305682

6. Произведем разделение секрета (рис.6 – 7). Так как программа позволяет вставить ключ длиной 16, то возьмём первые 16 бит ключа – 2609687163747682.

Рисунок 6 – Выбор параметров

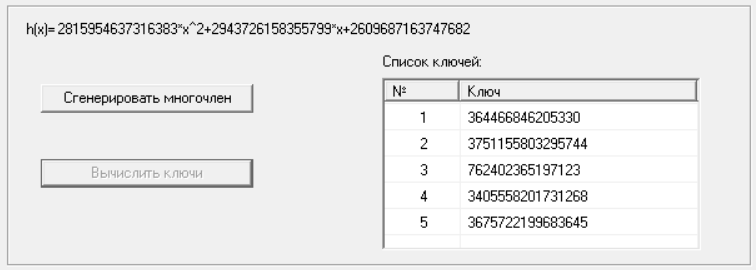
Рисунок 7 – Генерация многочлена и списка теней

7. Восстановим секрет по теням, выбрав тени 2, 3, 4 (рис.8 – 9).

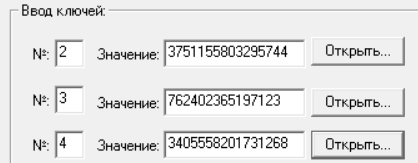
Рисунок 8 – Ввели значения теней

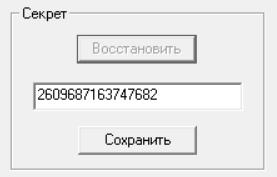
Рисунок 9 – Восстановили секрет

8. Добавим полученный секрет к оставшейся части ключа и получим:

Ключ: 260968716374768291162798789254627305682

9. Переведём ключ в шестнадцатеричную систему:

Ключ: C454BF1D571A2DCAA1835B4D399DA8D2

10. Проведём дешифрование полученной в пункте 3 криптограммы восстановленным секретом (рис.10).

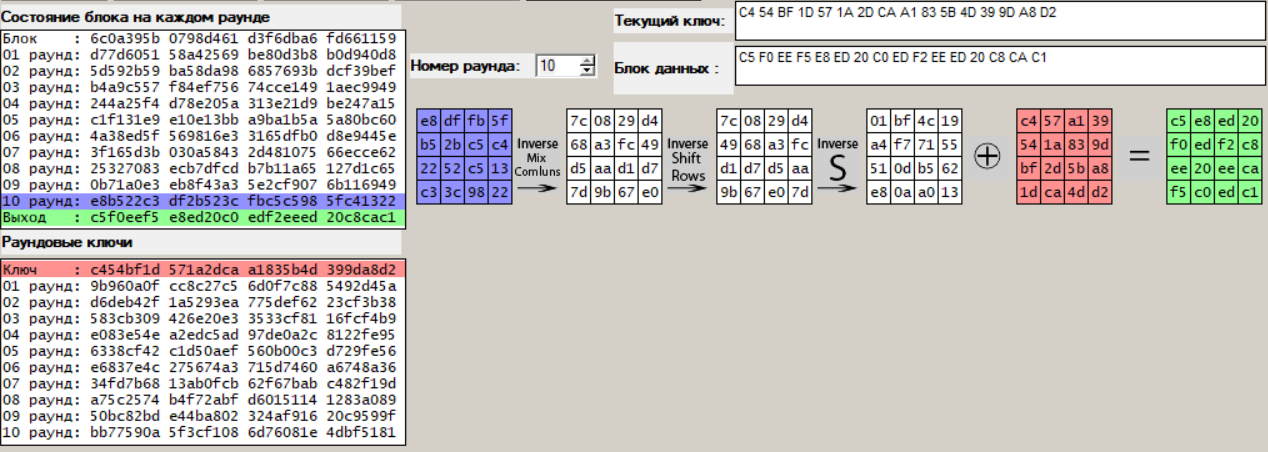
Рисунок 10 – Процесс дешифрования прошёл успешно

11. Полученный текст в шестнадцатеричном виде преобразуем в текст (рис.11).

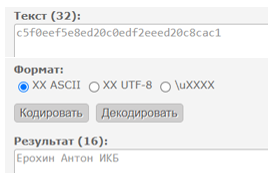
Рисунок 11 – Исходное сообщение

12. Сравним исходный текст и полученный в процессе дешифрования криптограммы (рис.12).

Рисунок 12 – Сравнение текстовых файлов

Так как тексты оказались идентичны, можно сделать вывод о правильности восстановления секрета (ключа шифрования).

13. Произведем изменение в тенях, выбранных в пункте 4 и попытаемся с помощью нового секрета дешифровать криптограмму (рис.13 – 14).

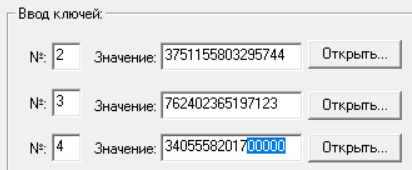
Рисунок 13 – Изменённые тени

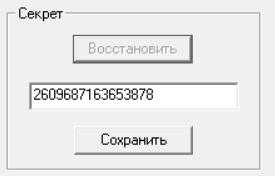
Рисунок 14 – Новый секрет

Добавим полученный секрет к оставшейся части ключа и получим:

Ключ: 260968716365387891162798789254627305682

Переведём ключ в шестнадцатеричную систему:

Ключ: C454BF1D38CAE4D3B11723423B9DA8D2

Введём новый ключ в программу «AES.exe» и произведём дешифрование (рис.15).

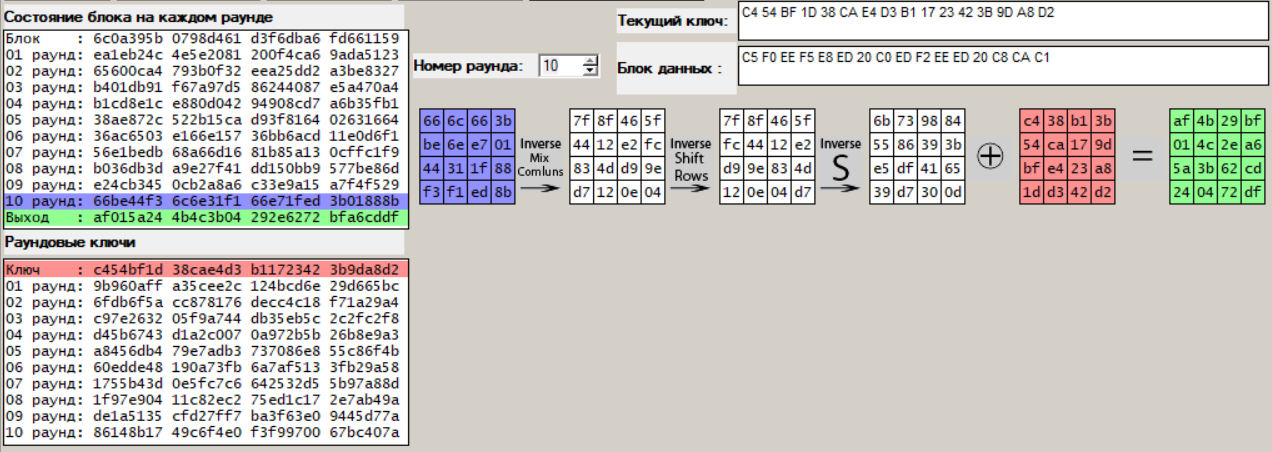
Рисунок 15 – Дешифрование

Полученный текст в шестнадцатеричном виде преобразуем в текст (рис.16).

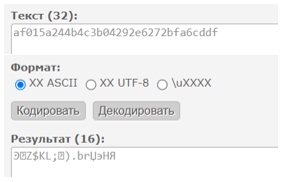
Рисунок 16 – Результат дешифрования

14. Сравним исходный текст и полученный в процессе дешифрования криптограммы (рис.17).

Рисунок 17 – Сравнение исходного текста и полученного

Можно сделать вывод, что дешифровать криптограмму с помощью секрета, восстановленного из неправильных теней, не удалось.

Вывод

В ходе выполнения лабораторной работы закрепили знания по теме «протоколы разделения секрета». В первой части работы провели моделирование схемы разделения секретов, где вручную, по заданным параметрам, сформировали полином, рассчитали тени и смогли восстановить секрет. Во второй части работы продемонстрировали практическое применение протокола разделения секрета на примере разделения ключа шифрования AES. После разделения ключа и расчёта теней удалось успешно восстановить секрет и с помощью него дешифровать криптограмму. При внесении ошибки в тени, был восстановлен другой секрет (ключ), что повлекло за собой дешифрование с ошибками.

Санкт-Петербург 2023 г