Лабораторная работа №6

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА» (СПбГУТ)

Факультет Инфокоммуникационных сетей и систем Кафедра Защищенных систем связи

Дисциплина Криптографические протоколы

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №6

Изучение криптосистемы Мак-Элис

(тема отчета)

Информационная безопасность (10.03.01)

(код и наименование направления/специальности)

Студент группы ИКБ-06:

Ерохин А.Г.

(Ф.И.О.) (подпись)

Д.т.н., проф. каф. ЗСС:

Яковлев В.А.

(Ф.И.О.) (подпись)

Цель работы:

Изучить преобразования, выполняемые при шифровании и дешифровании сообщений в крипто системе Мак-Элис, а также простейшие попытки ее взлома.

Используемое программное обеспечение:

Для работы используются специальные программы MAGMA.exe и McEliece.exe.

Ход работы:

1. Выбор параметров криптосистемы Мак-Элис:

• Длина информационного сообщения: k = 17 бит

• Длина кодового слова: n = 32 бита

• Количество искусственно вводимых ошибок: t = 3

2. Сгенерируем порождающую матрицу с помощью программы MAGMA (рис.1 – 2).

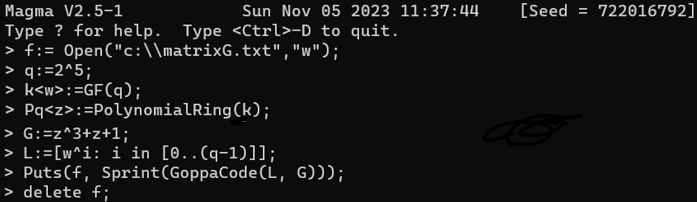
Рисунок 1 – Генерация матрицы

Рисунок 2 – Созданная матрица

3. Запустили программу McEliece.exe. Проверили, верны ли начальные данные для выбранных параметров при генерировании кода (рис.3).

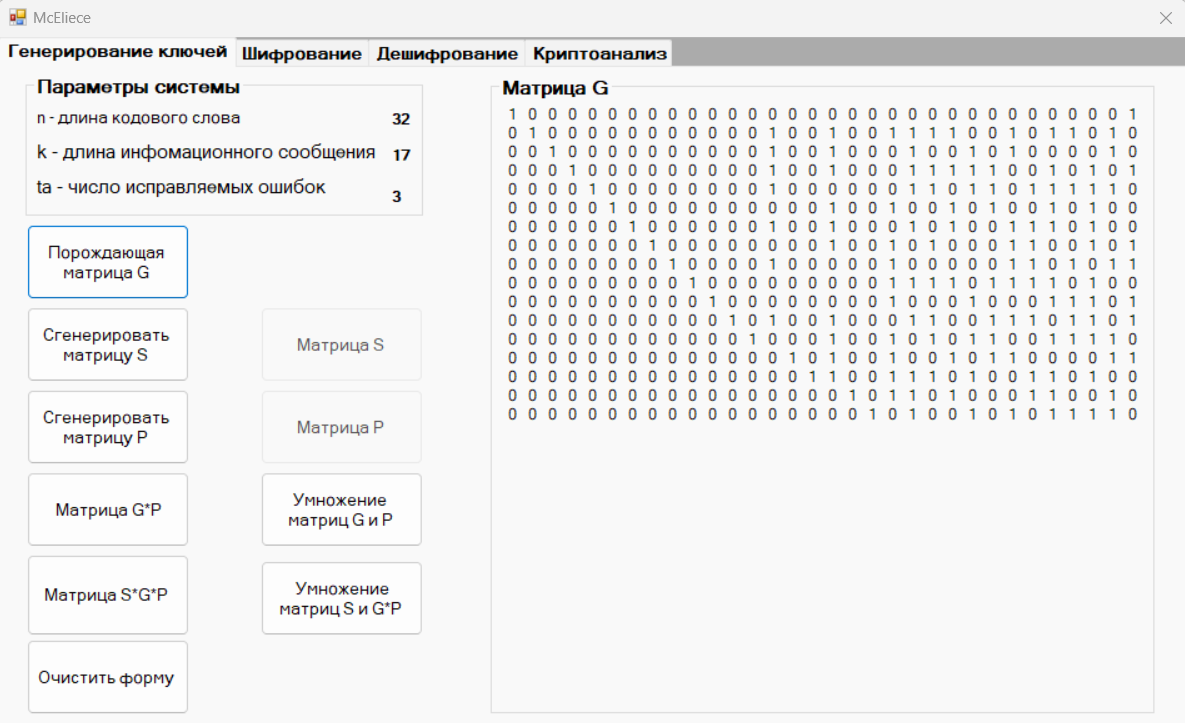
Рисунок 3 – Проверка начальных данных

4. Сгенерировали не сингулярную матрицу S (рис.4).

Рисунок 4 – Генерация матрицы S

5. Сгенерировали перестановочную матрицу P (рис.5).

Рисунок 5 – Генерация матрицы P

6. Рассчитали произведение матриц G и P (рис.6).

Рисунок 6 – Произведение матриц G и P

7. Рассчитали произведение матриц S и G*P (рис.7).

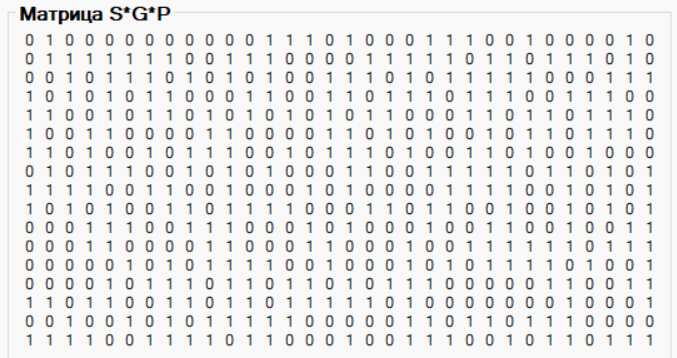
Рисунок 7 – Произведение матриц S и G*P

8. Определили закрытый и открытый ключи:

• Закрытый ключ: (G, S, P)

• Открытый ключ: (S*G*P, t_a)

9. Зададим двоичное сообщение и сгенерируем случайный вектор ошибок Z, найдем криптограмму (рис.8 – 10).

• Сообщение M1: 01011100010111011

• Вектор Z1: 01001000000000000000100000000000

• Криптограмма С1: 10100110101000010101000101011001

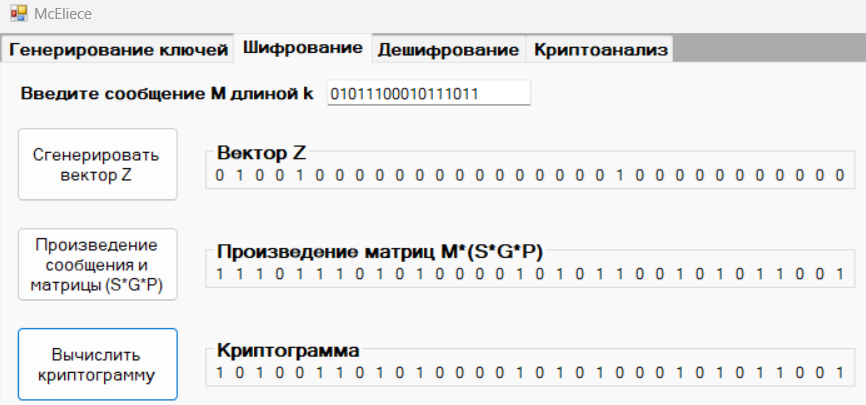
Рисунок 8 – Вычисление криптограммы С1

• Сообщение M2: 01011000000000000

• Вектор Z2: 10000000000000010000100000000000

• Криптограмма С2: 10011111011101011010110101001000

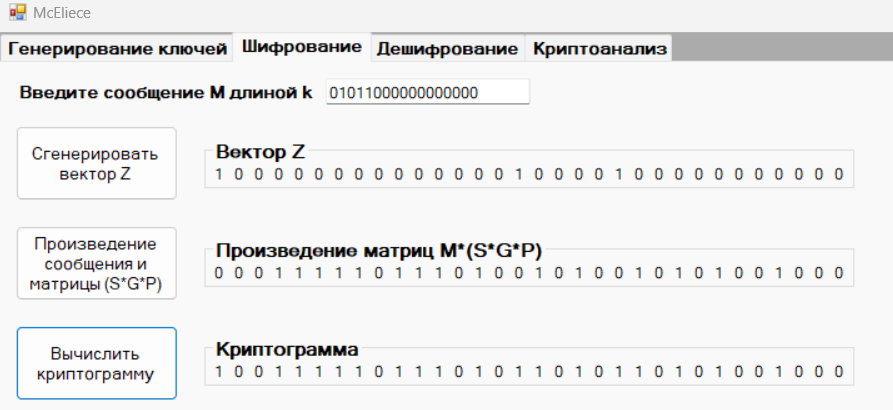
Рисунок 9 – Вычисление криптограммы С2

• Сообщение M3: 01011111111111111

• Вектор Z3: 00000010000000100000000000001000

• Криптограмма С3: 01010100100110011001101110111011

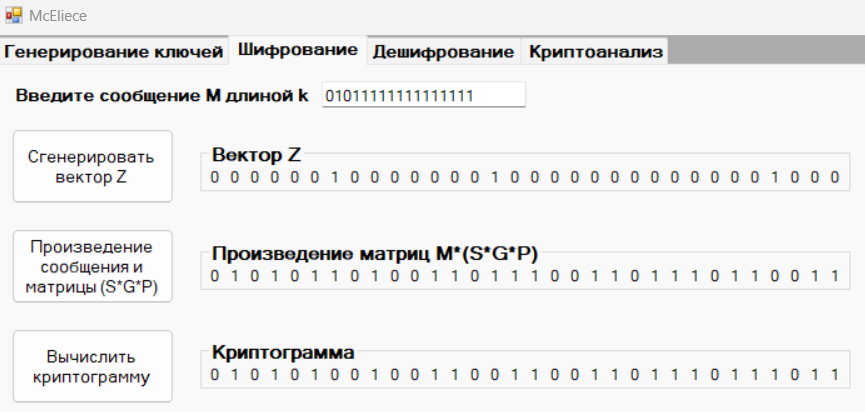
Рисунок 10 – Вычисление криптограммы С3

10. Выполним дешифрование полученных криптограмм (рис.11 – 13).

Рисунок 11 – Дешифрование криптограммы C1

• Расшифрованное сообщение: 01011100010111011

Расшифрованное сообщение совпадает с заданным сообщением M1, следовательно процесс дешифрования прошёл успешно.

Рисунок 12 – Дешифрование криптограммы C2

• Расшифрованное сообщение: 01011000000000000

Расшифрованное сообщение совпадает с заданным сообщением M2, следовательно процесс дешифрования прошёл успешно.

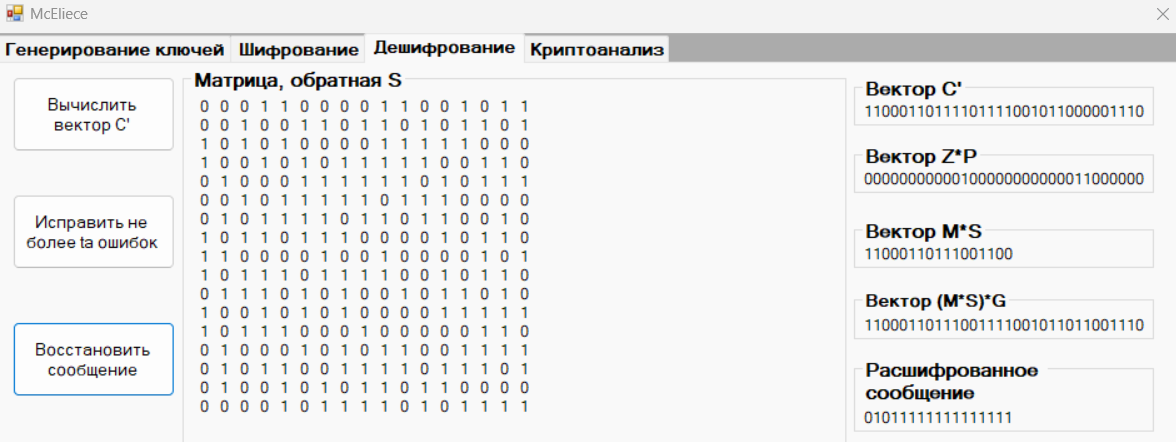
Рисунок 13 – Дешифрование криптограммы C3

• Расшифрованное сообщение: 01011111111111111

Расшифрованное сообщение совпадает с заданным сообщением M3, следовательно процесс дешифрования прошёл успешно.

11. Выполнили атаку на криптосистему (рис.14 – 16).

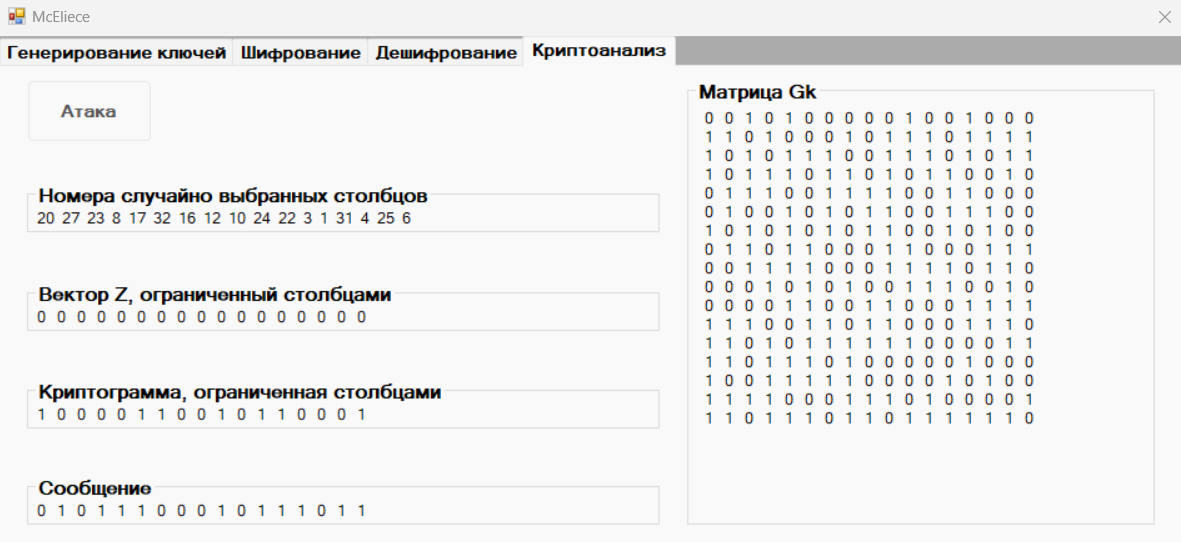
Рисунок 14 – Результаты атаки

• Номера столбцов: 20 27 23 8 17 32 16 12 10 24 22 3 1 31 4 25 6

• Нулевой вектор Z: 00000000000000000

• Восстановленное сообщение M1: 01011100010111011

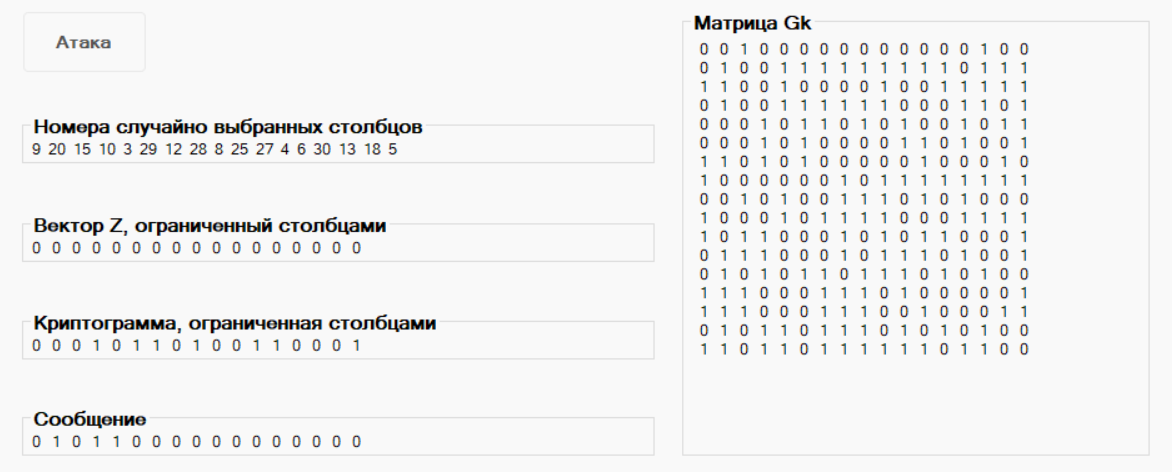
Рисунок 15 – Результаты атаки

• Номера столбцов: 9 20 15 10 3 29 12 28 8 25 27 4 6 30 13 18 5

• Нулевой вектор Z: 00000000000000000

• Восстановленное сообщение M2: 01011000000000000

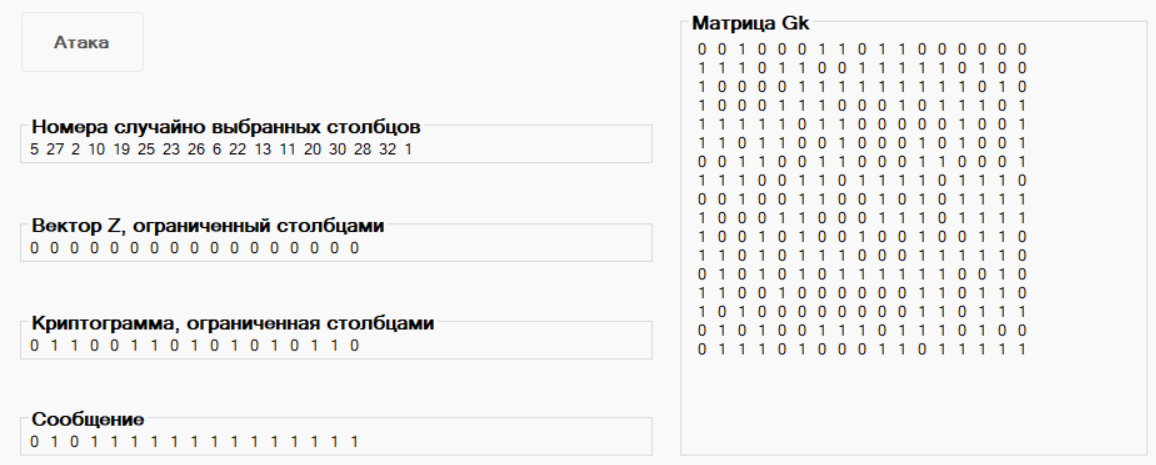
Рисунок 16 – Результаты атаки

• Номера столбцов: 5 27 2 10 19 25 23 26 6 22 13 11 20 30 28 32 1

• Нулевой вектор Z: 00000000000000000

• Восстановленное сообщение M3: 01011111111111111

В ходе атаки на криптосистему были успешно получены все три сообщения, следовательно атака была проведена успешно.

12. Расчёт вероятностей успешной атаки для различных значений n, k, t.

Вероятность того, что вектор Z окажется нулевым вычисляется по формуле:

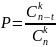
Рассчитаем вероятность при n = 32, k = 17, t = 3:

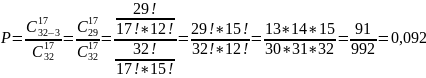
Рассчитаем вероятность при n = 16, k = 4, t = 3:

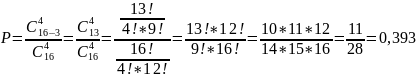
Рассчитаем вероятность при n = 8, k = 2, t = 2:

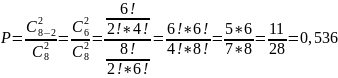
При увеличении параметров n, k, t КС Мак-Элис вероятность успешной атаки становится меньше. Для обеспечения высокой стойкости криптосистемы рекомендуются следующие параметры:

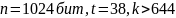
Вывод:

В ходе выполнения лабораторной работы изучили КС Мак-Элис. Успешно сгенерировали порождающую матрицу G на основе выбранных параметров криптосистемы. Далее сгенерировали несингулярную матрицу S и перестановочную матрицу P. Полученные матрицы представляют собой закрытый ключ криптосистемы (G, S, P). Успешно вычислили матрицу S*G*P, которая вместе с количеством искусственно введённых ошибок t_a являются открытым ключом (S*G*P, t_a). На основе вычисленных ключей произвели успешное шифрование и дешифрование трёх сообщений. В заключительной части работы произвели атаку на криптосистему Мак-Элис, а также рассчитали вероятности успешной атаки на криптосистему для различных значений n, k, t.

Санкт-Петербург 2023 г