Лабораторная работа №5

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА» (СПбГУТ)

Факультет Инфокоммуникационных сетей и систем Кафедра Защищенных систем связи

Дисциплина Криптографические протоколы

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №5

Изучение квантового алгоритма Шора факторизации модуля криптосистемы РША

(тема отчета)

Информационная безопасность (10.03.01)

(код и наименование направления/специальности)

Студент группы ИКБ-06:

Ерохин А.Г.

(Ф.И.О.) (подпись)

Д.т.н., проф. каф. ЗСС:

Яковлев В.А.

(Ф.И.О.) (подпись)

Цель работы:

Ознакомление с квантовым алгоритмом факторизации Шора и основами квантовых вычислений, наблюдение принципа работы квантового алгоритма в симуляции. Изучение способа факторизации модуля методом поиска периода для взлома криптосистем РША.

Используемое программное обеспечение:

Для работы используются программы QuantumSimulator.exe и ContFrac.exe из учебного каталога.

Ход работы:

1. Провести факторизацию числа M путём вычисления периода функции 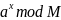вручную. Для этого найти период методом простого перебора. Работа выполняется в соответствие с вариантом 11.

Таблица 1 – Исходные данные

№
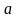
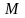
11	8	91

Проверим, что числа M и a – взаимно простые:

НОД(91, 8) = НОД(91-8*11, 8) = НОД(3,8) =НОД(3, 8-3*2) = НОД(3,2)=1

Найдем период этой функции с помощью перебора всех возможных значений. Значения запишем в таблицу 2.

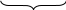Таблица 2 – Перебор значений

х	0	1	2	3	4	5	6	7	8	…
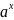
	1									…
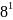
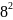
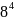
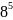
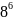
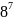
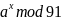
	1	8	64	57	1	8	64	57	1	…

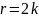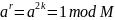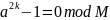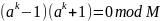Из таблицы 2 видно, что период повторения функции . Поскольку r – четное, то его можно представить как . Тогда получим или . Тогда, используя формулу разности квадратов, запишем и , что означает наличие общего множителя у M и 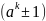. Следовательно, с помощью алгоритма Евклида мы можем найти числа p и q как 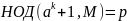и .

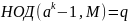Для из имеем:

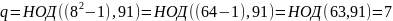
Проверяем: . Далее на основании известных p и q для криптосистемы РША можно вычислить функцию Эйлера и секретный ключ.

Таким образом, была произведена успешная факторизация модуля 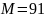и получено его разложение как

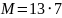
2. Ознакомиться с квантовой частью алгоритма Шора и выполнить вручную процесс квантового возведения в степень в виде записи состояния регистров для двух периодов. Выбрать любое значение и составить для него суперпозицию состояний регистра .

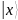Для варианта 11 получаем: , .

Тогда

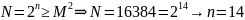
Шаг 0 (подготовительный этап). Все кубиты квантовых регистров устанавливаются в нулевое состояние вида:

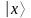
Шаг 1 (равновероятное состояние). К каждому кубиту первого регистра применим преобразование Адамара. В результате регистр 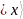переводится к равновероятной суперпозиции всех возможных состояний:

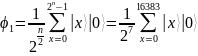
Шаг 2 (возведение в степень). Вычисляются значения функции 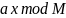для всех х первого регистра, результаты записываются во второй регистр. В результате регистры будут в состояниях:

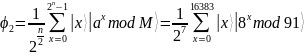
Тогда каждому фиксированному состоянию регистра 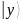, соответствует последовательность значений регистра (табл.3).

Таблица 3 – Состояния регистров

…	…	…	…
…	…	…	…

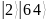
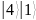
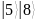
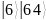
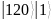
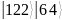
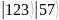
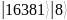
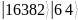
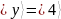После измерения состояния регистра в соответствии с заданием мы получили фиксированное состояние , которому соответствует последовательность значений х вида:

где , – сдвиг относительно начала координат (нулевого состояния регистра , ).

Таким образом, было рассмотрено состояние регистров на этапе выполнения квантового возведения в степень и получена суперпозиция состояний в регистре , соответствующих фиксированному состоянию регистра = 64.

3. Выполнить факторизацию числа М на основе квантового алгоритма Шора с помощью программы-симулятора QuantumSimulator.exe, проанализировать полученные результаты и сделать выводы.

Модуль М = 91, a = 8 выбраны в соответствии с вариантом 11. Запустили программу QuantumSimulator.exe и выбрали «Ручной ввод» (рис.1).

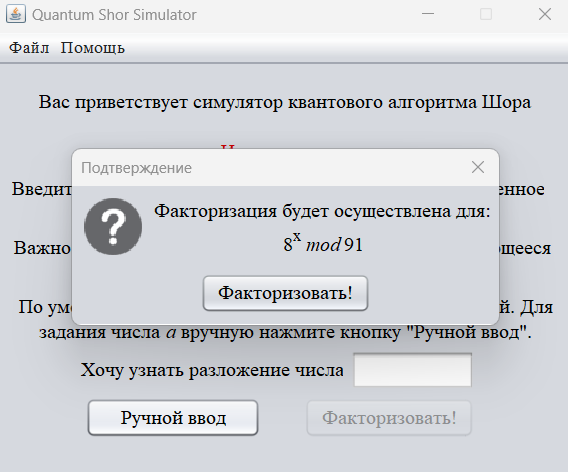
Рисунок 1 – Запуск программы

Рассмотрим процесс симуляции выполнения квантового алгоритма Шора. Необходимое для задания размера квантовых регистров и, соответственно, в этом случае количество состояний каждого регистра 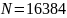(рис.2).

Рисунок 2 – Справочные материалы

Далее в программе следует процесс инициализации – все кубиты квантовых регистров устанавливаются в нулевое состояние: (рис.3).

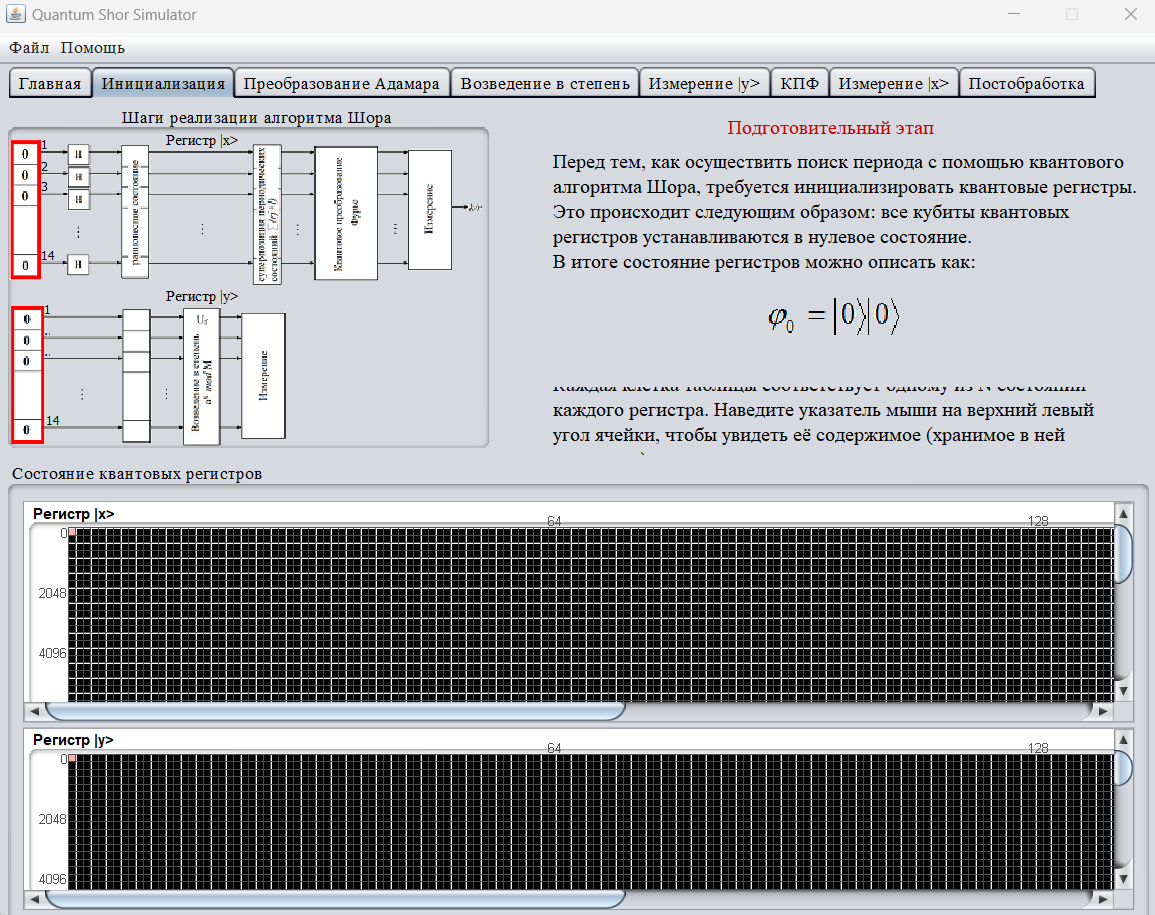
Рисунок 3 – Инициализация

Затем выполняется преобразование Адамара к каждому кубиту первого регистра. В результате регистр переводится к равновероятностной суперпозиции всех возможных состояний (рис.4).

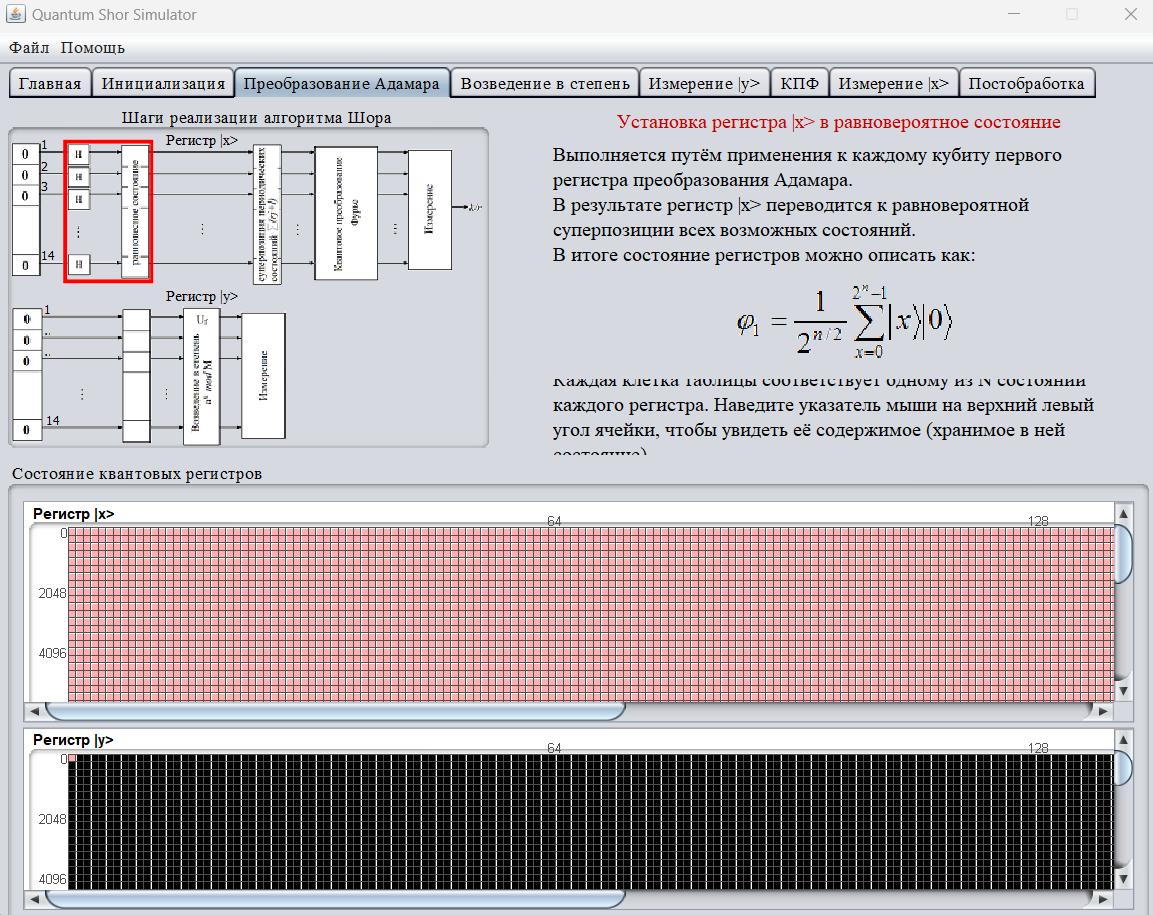
Рисунок 4 – Преобразование Адамара

В результате выполнения квантового возведения в степень на следующем этапе для функции для всех состояний регистра , в регистре были получены следующие значения {1, 8, 57, 64} (рис.5).

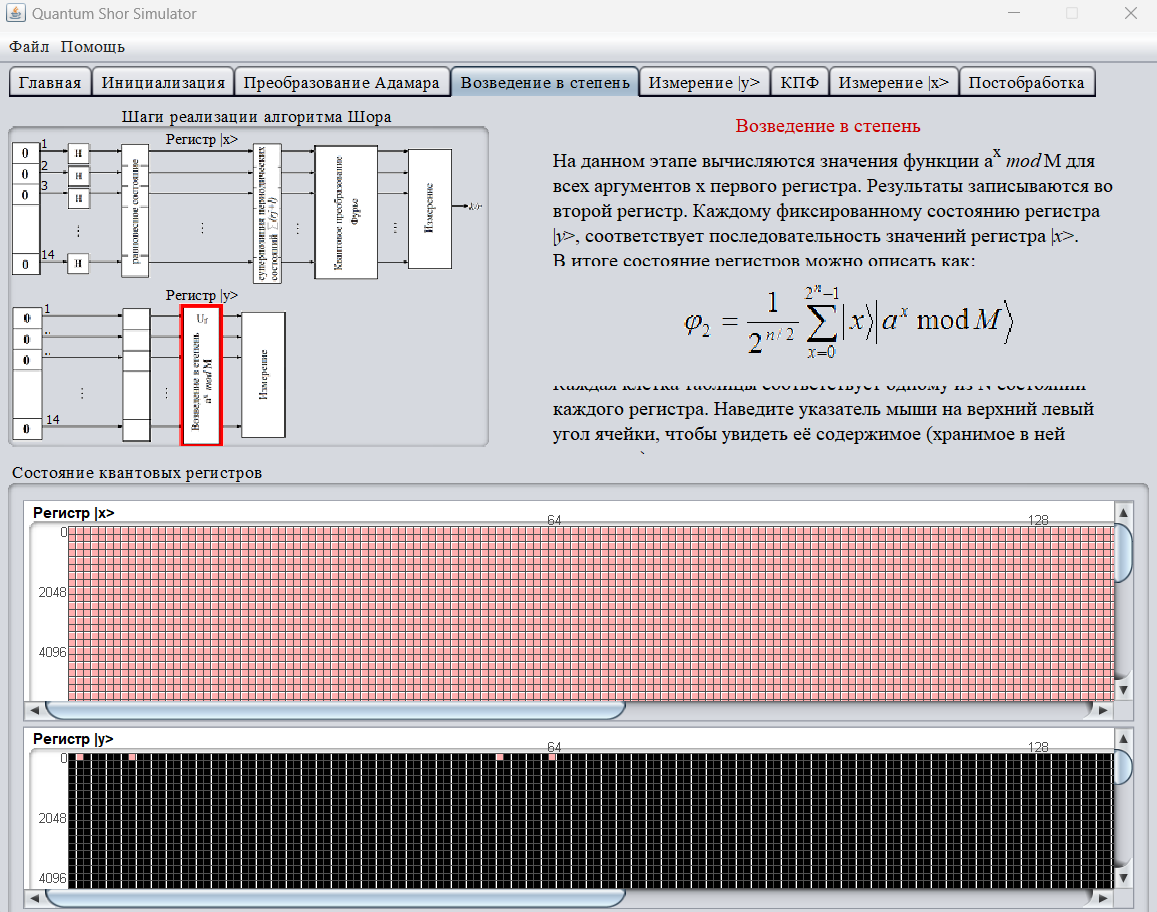
Рисунок 5 – Возведение в степень

Далее было произведено измерение состояния регистра , было получено фиксированное значение y = 64, которому соответствует суперпозиция периодических последовательностей состояний в регистре (рис.6).

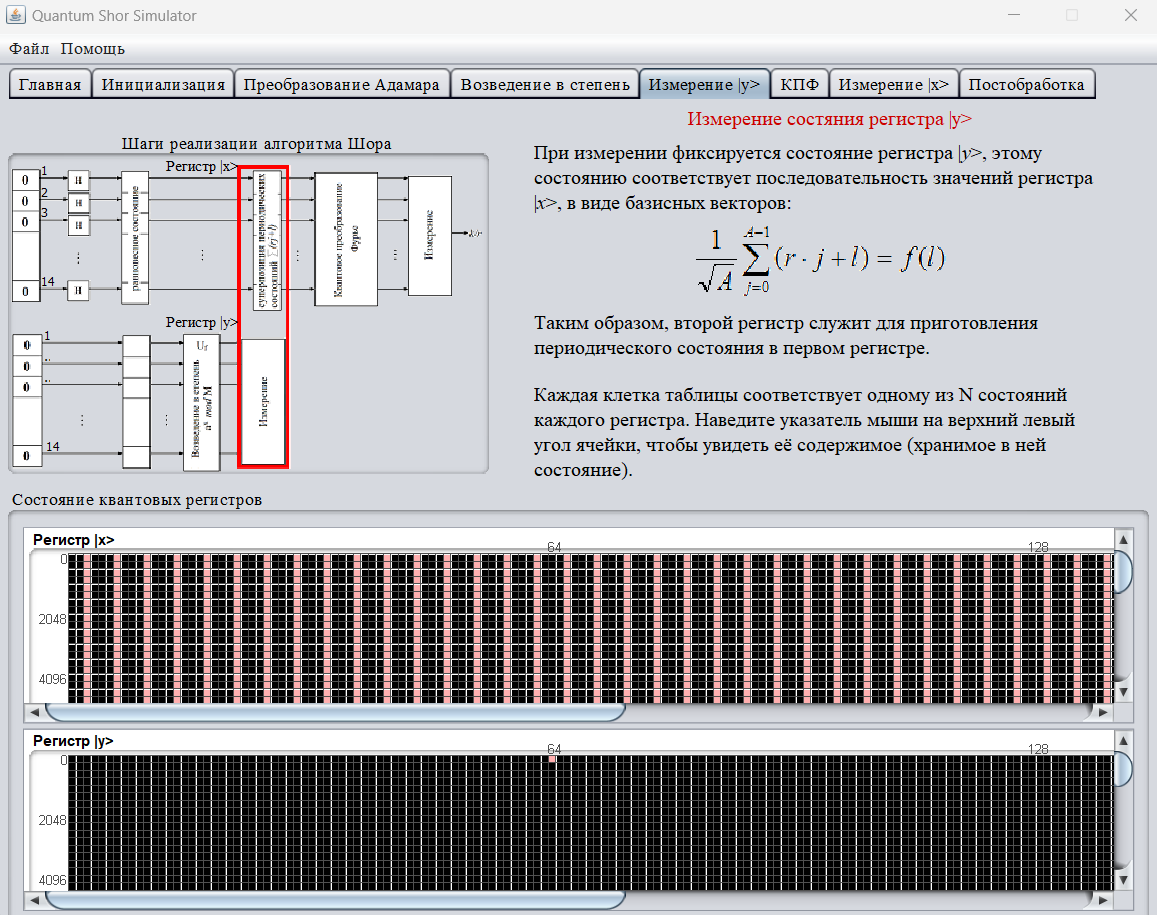
Рисунок 6 – Фиксированное значение y

Суперпозиция описывается следующим образом:

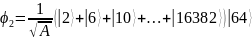
В результате применения для суперпозиции, содержащейся в регистре , квантового преобразования Фурье, были получены следующие значения {0, 4096} (рис.7).

Рисунок 7 – Квантовое преобразование Фурье

В результате измерения состояния регистра из упомянутого множества значений, было выбрано фиксированное значение m = 4096 (рис.8).

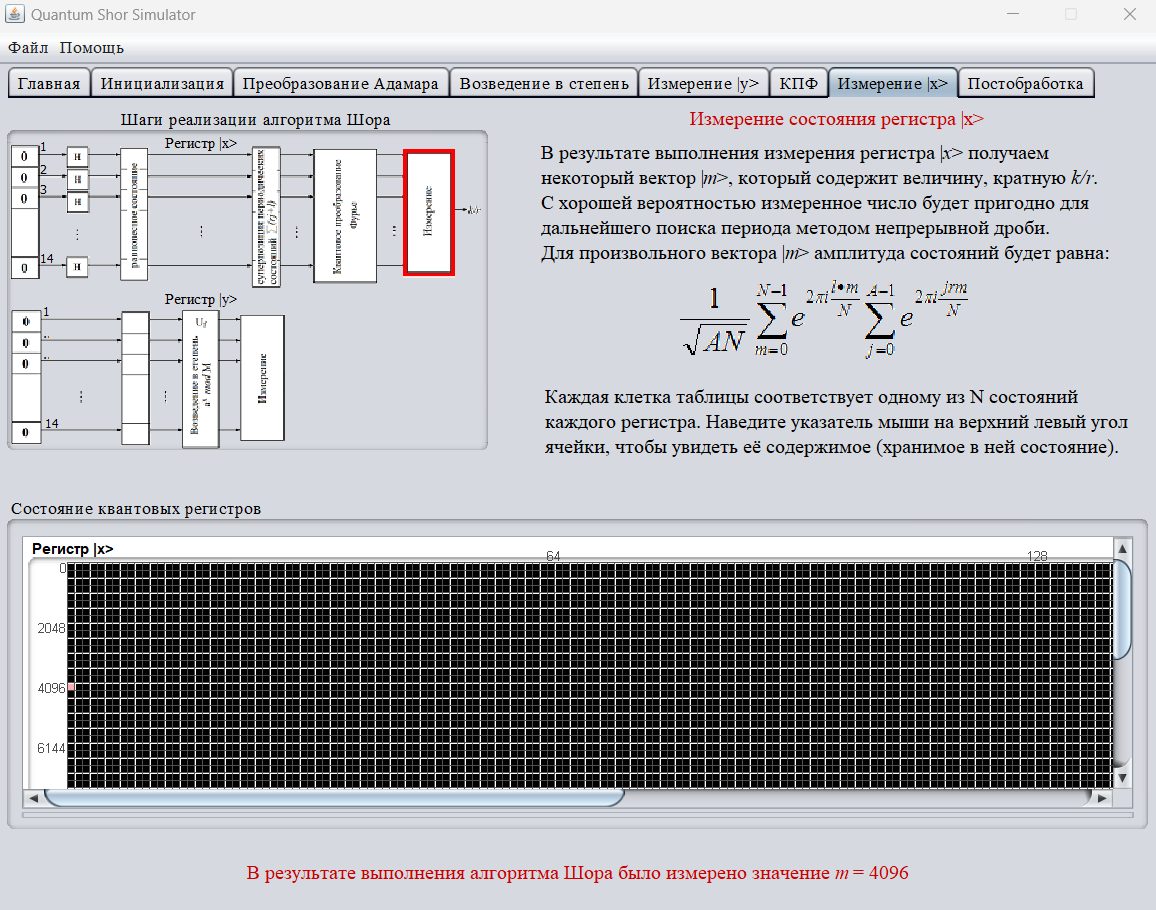
Рисунок 8 – Измерение состояния регистра x

Дробь вида 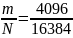передается на постобработку (рис.9).

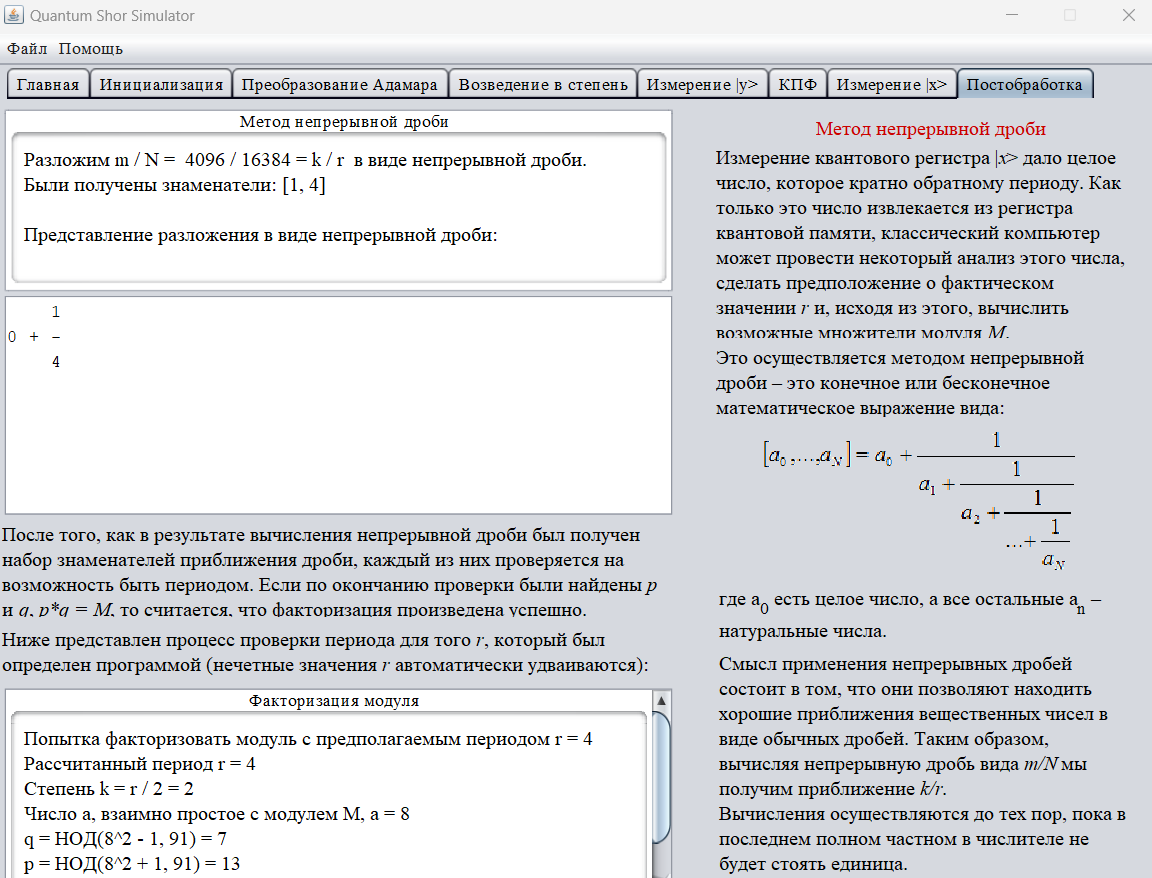
Рисунок 9 – Постобработка

Получаем разложение непрерывной дроби 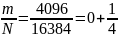. Находим возможные периоды .

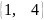Из тих периодов условиям, необходимым для определения истинного периода, удовлетворяет только : 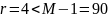и 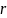– четное число.

На основании полученного значения рассчитаем коэффициенты разложения :

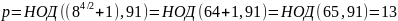
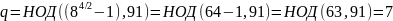
Очевидно, что факторизация была произведена успешно. Проверяем: (рис.10).

Рисунок 10 – Постобработка

Следовательно, значение модуля успешно факторизовано, значит, криптосистема РША может быть взломана.

Вывод:

В ходе выполнения лабораторной работы было осуществлено ознакомление с квантовым алгоритмом факторизации Шора и основами квантовых вычислений. На первом этапе работы произвели факторизацию числа M с помощью ручного перебора, успешно нашли период r и смогли вычислить p и q. Во второй части работы познакомились с квантовой частью алгоритма Шора и выполнили вручную процесс квантового возведения в степень в виде записи состояния регистров для двух периодов. В заключительной части работы выполнили факторизацию числа М на основе квантового алгоритма Шора с помощью программы-симулятора QuantumSimulator.exe. Результаты факторизации «вручную» и с использование программы совпали, следовательно факторизация была выполнена верно. Возможность произвести факторизацию числа M приводит к тому, что криптосистема РША может быть взломана.

Санкт-Петербург 2023 г