Лабораторная работа №4
.docxМИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА» (СПбГУТ)
Факультет Инфокоммуникационных сетей и систем Кафедра Защищенных систем связи
Дисциплина Криптографические протоколы
ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №4
Исследование побочных атак на криптосистему РША
(тема отчета)
Информационная безопасность (10.03.01)
(код и наименование направления/специальности)
Студент группы ИКБ-06:
Ерохин А.Г.
(Ф.И.О.) (подпись)
Д.т.н., проф. каф. ЗСС:
Яковлев В.А.
(Ф.И.О.) (подпись)
Цель работы:
Изучить влияние параметров и способов проектирования криптосистемы РША на возможность ее криптоанализа, используя побочные атак, а также закрепить знания, полученные на лекциях курса «Основы криптографии с открытым ключом», «Криптографические протоколы».
Используемое программное обеспечение:
Для выполнения работы используется специально разработанный программный комплекс «RSA attacks lab.exe»
Ход работы:
Атака на малую шифрующую экспоненту
Сгенерировать 3 набора ключей РША с одинаковой малой открытой экспонентой e=3. Сгенерировать случайное сообщение и зашифровать его:
Сообщение: 731
Криптограмма 1: 160190
Криптограмма 2: 1361
Криптограмма 3: 3832
Вычисление решения системы уравнений: 390617891
Нахождение кубического корня методом Ньютона: 731
Как мы можем увидеть, полученный кубический корень методом Ньютона полностью совпадает с нашим сообщением, следовательно атака была проведена успешно (рис.1).
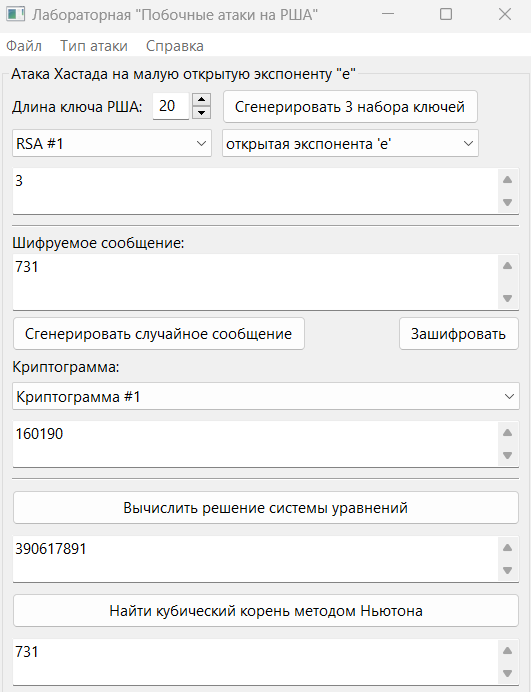
Рисунок 1 – Атака на малую шифрующую экспоненту
Атака при малом количестве возможных сообщений
Сгенерировать ключи криптосистемы и список возможных сообщений заданной длины.
Возможное сообщение 1: 763
Возможное сообщение 2: 675
Возможное сообщение 3: 68
Возможное сообщение 4: 904
Возможное сообщение 5: 1105
Возможное сообщение 6: 1398
Возможное сообщение 7: 80
Возможное сообщение 8: 559
Возможное сообщение 9: 1204
Возможное сообщение 10: 416
Зашифруем случайным образом одно из возможных сообщений:
Получили криптограмму: 856
Будем последовательно шифровать возможные сообщения из списка, до тех пор, пока на выходе не получим начальную криптограмму 856.
Сообщение 1 (763) – криптограмма: 298
Сообщение 2 (675) – криптограмма: 213
Сообщение 3 (68) – криптограмма: 1379
Сообщение 4 (904) – криптограмма: 319
Сообщение 5 (1105) – криптограмма: 1075
Сообщение 6 (1398) – криптограмма: 45
Сообщение 7 (80) – криптограмма: 884
Сообщение 8 (559) – криптограмма: 856
Шифруя сообщение 8-ое получили начальную криптограмму 856 (рис.2). Таким образом, исходное сообщение: 559.
Рисунок 2 – Атака при малом количестве возможных сообщений
Скорость данной атаки зависит от количества возможных сообщений. Чем больше будет сообщений, тем больше времени уйдёт на случайное обнаружение нужной криптограммы.
Атака Винера
Сгенерировать ключи криптосистемы. Выполнить атаку Винера.
Длина модуля РША: 40
Длина секретной экспоненты: 10
Открытая экспонента e: 197728783417
Модуль криптосистемы n: 318391291343
Секретная экспонента d: 409
Простое число p: 881099
Простое число q: 361357
Выполним атаку Винера с помощью программы (рис.3).
Рисунок 3 – Атака Винера
Подтвердим успешность выполнения атаки ручными расчетами.
Секретную
экспоненту вычислим как знаменатель
подходящей дроби в неравенстве
Используя алгоритм Евклида, найдем цепную дробь рационального числа:
Вычислим подходящие дроби:
Теперь
для каждой подходящей дроби будем
находить функцию Эйлера согласно
выражению
, и решать квадратное уравнение
.
Если
корни уравнения p и q целочисленные,
простые, и выполняется равенство
,
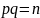то секретная экспонента найдена
правильно. В противном случае, проверяем
следующую подходящую дробь.
Равенство выполняется, следовательно, секретная экспонента d = 409 найдена правильно, делители модуля p = 881099, q = 361357 найдены верно.
Попробуем провести атаку Винера, используя битовую длину секретную экспоненты больше, чем четверть битовой длины модуля КС (рис.4).
Рисунок 4 – Атаку выполнить не удалось
При битовой длине секретной экспоненты больше четверти битовой длины модуля КС атаку выполнить не удалось.
Атака с использованием мультипликативного свойства шифра РША
Параметры криптосистемы:
Открытая экспонента e: 1221
Модуль криптосистемы n: 2481
Секретная экспонента d: 1629
Выбранное сообщение M: 1640
Зашифрованное сообщение C: 488
Случайное число x взаимно простое с модулем n: 1867
Комбинированная криптограмма C’ = C * xe mod n = 1121
Расшифрованное M’: 326
Исходное сообщение M = M’ * x-1 mod n = 1640
Атака проведена успешно, получили исходное сообщение M (рис.5).
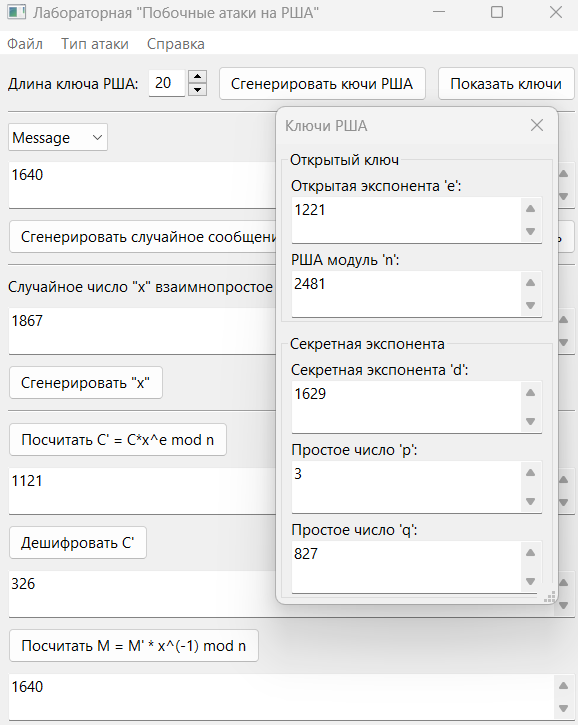
Рисунок 5 – Атака с использованием мультипликативного свойства шифра РША
Циклическая атака
Открытая экспонента e: 18671
Модуль криптосистемы n: 134041
Секретная экспонента d: 83831
Шифруемое сообщение M: 126429
Криптограмма C: 18326
,
где k = 105
Исходное
сообщение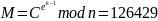
Атака проведена успешно, получили исходное сообщение M (рис.6).
Рисунок 6 – Циклическая атака
Увеличим длину модуля КС и проведем еще одну атаку (рис.7).
Рисунок 7 – Не удалось выполнить циклическую атаку
Таким образом, мы убедились, что алгоритм выполнения данной атаки обладает не полиноминальной сложностью.
Атака на общие модули
Открытая экспонента e1: 90533
Открытая экспонента e2: 51457
Секретная экспонента d1: 126251
Общий модуль n: 126251
Случайное число g, используемое для факторизации: 53513
Нечётное число k: 371168325
Делители модуля: 191 и 661
Секретная экспонента d2: 84193
Атака проведена успешна, секретная экспонента второго пользователя d2 действительна равняется 84193 (рис.8).
Рисунок 8 – Атака на общие модули
Вывод
В ходе выполнения лабораторной работы было изучено виляние параметров и способов проектирования КС РША на возможность ее криптоанализа, используя побочные атаки. В результате работы было проведено 6 побочных атака. Во всех случаях результаты атаки были успешны. Однако удалось установить, что не все виды атак обладают полиномиальной сложностью (циклическая атака).
Санкт-Петербург 2023 г