Лабораторная работа №2

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА» (СПбГУТ)

Факультет Инфокоммуникационных сетей и систем Кафедра Защищенных систем связи

Дисциплина Криптографические протоколы

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №2

Тестирование простых чисел и нахождение квадратичных вычетов

(тема отчета)

Информационная безопасность (10.03.01)

(код и наименование направления/специальности)

Студент группы ИКБ-06:

Ерохин А.Г.

(Ф.И.О.) (подпись)

Д.т.н., проф. каф. ЗСС:

Яковлев В.А.

(Ф.И.О.) (подпись)

Цель работы:

Закрепить знания, полученные на лекциях лисциплины «криптопротоколы» по разделам: “Квадратичные вычеты” и “Генерирование и тестирование простых чисел”.

Используемое программное обеспечение:

Для работы используется программа “Maxima” и дополнительные командные строки для решения каждой из задач.

Ход работы:

Задание 1.

1. Перешли к пакету «Maxima».

2. Рассчитали вероятность попадания на простое число при случайном генерировании чисел разрядности l=100, 300, 500 и 1000 при помощи следующей команды:

l:…..;

lg(x) := log(x)/log(10);

EstimateProb:2*(9*l-10)/(9*l*(l-1)*lg(10));

Ввод команд осуществлять построчно. Вместо переменных предпочтительнее подставлять конкретные числовые значения, получаемые в ходе работы (рис.1 – 4).

Рисунок 1 – Вероятность попадания на простое число при разрядности l = 100

Рисунок 2 – Вероятность попадания на простое число при разрядности l = 300

Рисунок 3 – Вероятность попадания на простое число при разрядности l = 500

Рисунок 4 – Вероятность попадания на простое число при разрядности l = 1000

3. Для проверки числа на простоту тестом Ферма сгенерировать необходимое количество случайных 3-х разрядных чисел при помощи команды: U:100+random(900);

и отобрать среди них не менее 3 нечетных чисел m, среди которых должно быть одно простое число (рис.5).

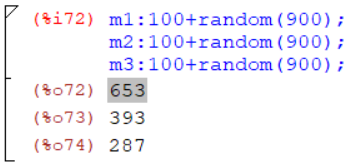
Рисунок 5 – Генерация 3-х разрядных чисел, одно из которых простое

Сгенерировать не менее 5 случайных 2-х разрядных чисел a при помощи команды: U:10+random(90) (рис.6).

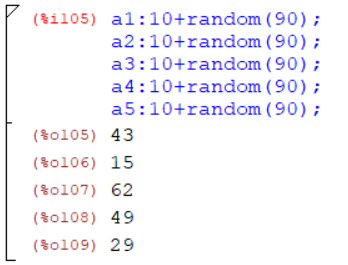
Рисунок 6 – Генерация случайных 2-х разрядных чисел

Произвести проверку чисел m на простоту, используя тест Ферма при помощи команды: power_mod(a,m-1,m) (рис.7 – 9).

Для m1 = 653:

Рисунок 7 – Тест Ферма для числа 653

Результаты теста Ферма. Число 653 является простым с итоговой вероятностью: .

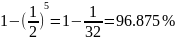Вероятность ошибки: .

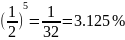Для m2 = 393:

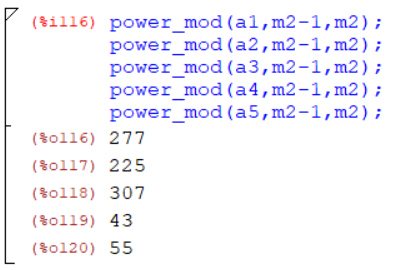
Рисунок 8 – Тест Ферма для числа 393

Результаты теста Ферма. Число 393 является составным.

Для m3 = 287:

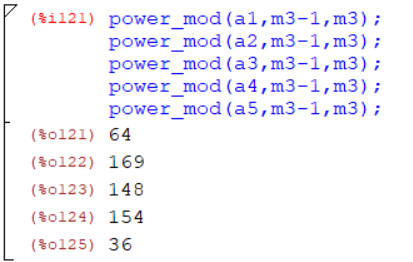
Рисунок 9 – Тест Ферма для числа 287

Результаты теста Ферма. Число 287 является составным.

4. Произвести тестирования числа Кармайкла m=561 по методу Ферма. Для этого сгенерировать необходимое количество случайных 2-х разрядных чисел по п. 3 и далее выбрать из них не менее 5 чисел a’ взаимно простых с 561, используя команды: gcd(a’,561);

Проверить число 561, используя тест Ферма по п. 3. (рис.10).

Рисунок 10 – Тест Ферма для числа Кармайкла 561

В ходе выполнения проверки числа Кармайкла m = 561 было ложно выявлено, что число является вероятно простым с вероятностью 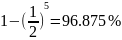. Для чисел Кармайкла тест Ферма использовать нецелесообразно, ведь для них результат теста является ложным для всех чисел a’, не являющихся делителем такого числа.

5. Произвести тестирование на простоту одного из чисел m, сгенерированных в п.3 и число Кармайкла 561, по методу Миллера–Рабина (рис.11 – 12).

Для m = 561:

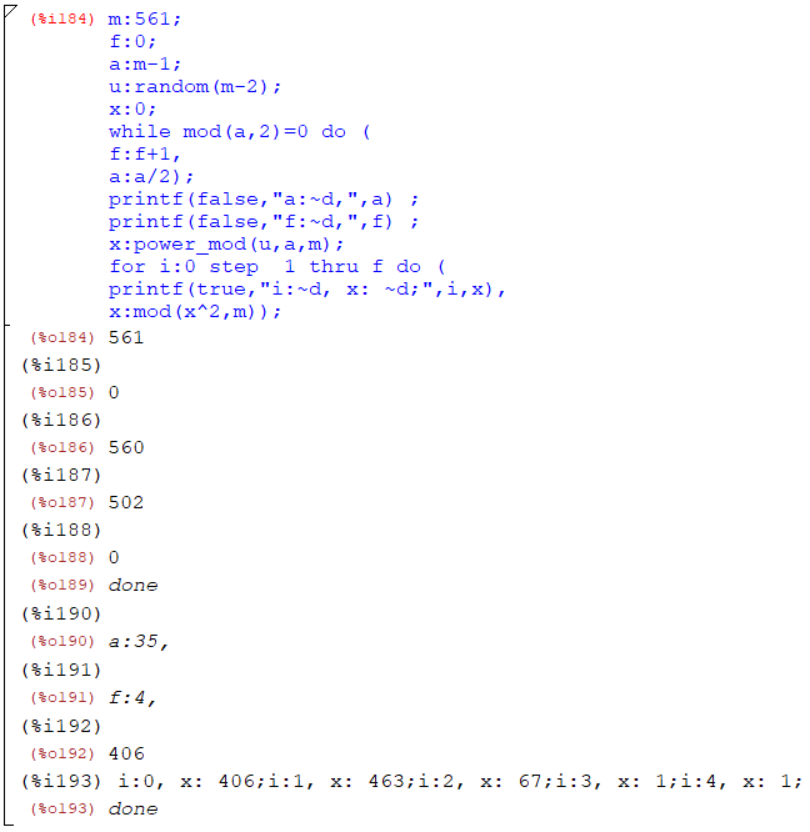
Рисунок 11 – Тест Миллера-Рабина для числа Кармайкла 561

Результат теста Миллера-Рабина. Число 561 – составное число.

Для m = 287:

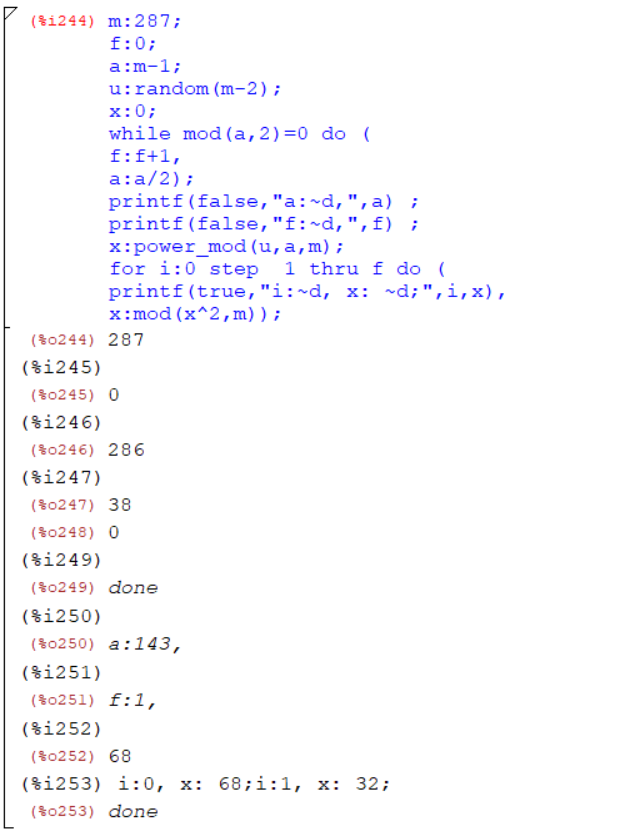
Рисунок 12 – Тест Миллера-Рабина для числа 287

Результат теста Миллера-Рабина. Число 287 – составное число.

Тест на простоту по методу Миллера-Рабина оказался эффективнее теста Ферма.

6. Найти несколько квадратичных вычетов (рис.13) u<m по mod(m), где m одно из простых 3-х разрядных чисел, используя вычисление символа Якоби (который для простых m совпадает с символом Лежандра).

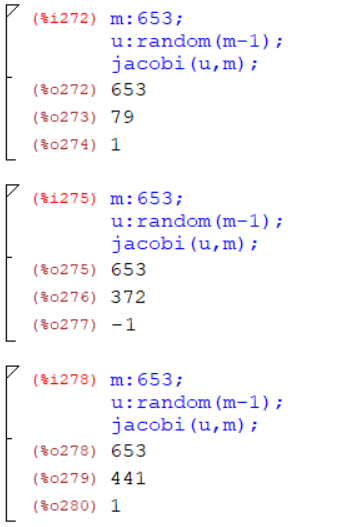
Рисунок 13 – Вычисление квадратичных вычетов

Нашли 2 квадратичных вычета по модулю 653 – это числа 79, 441.

И, для примера, нашли 1 квадратичный невычет – число 372.

Задание 2.

Вариант выполнения задания – 11.

1. Распределите числа в поле GF(p) на вычеты и невычеты p = 17.

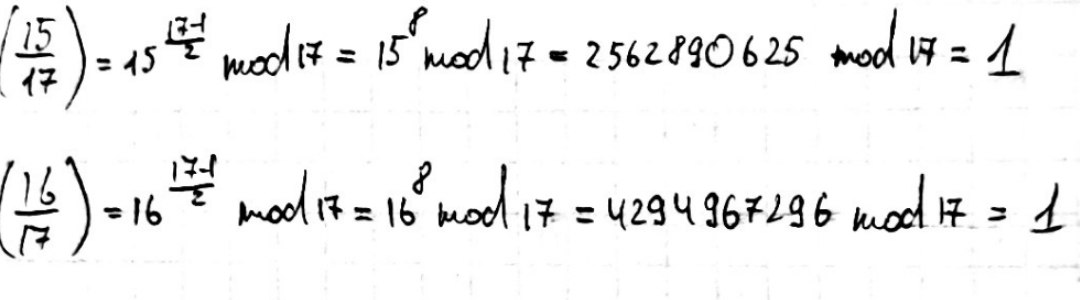
Квадратичными вычетами являются классы вычетов: [1]₁₇, [2]₁₇, [4]₁₇, [8]₁₇, [9]₁₇, [13]₁₇, [15]₁₇, [16]₁₇

Квадратичными невычетами являются классы вычетов: [3]₁₇, [5]₁₇, [6]₁₇, [7]₁₇, [10]₁₇, [11]₁₇, [12]₁₇, [14]₁₇

2. Проверьте, является ли число а=(№вар+20) mod31 вычетом по модулю 17, 19.

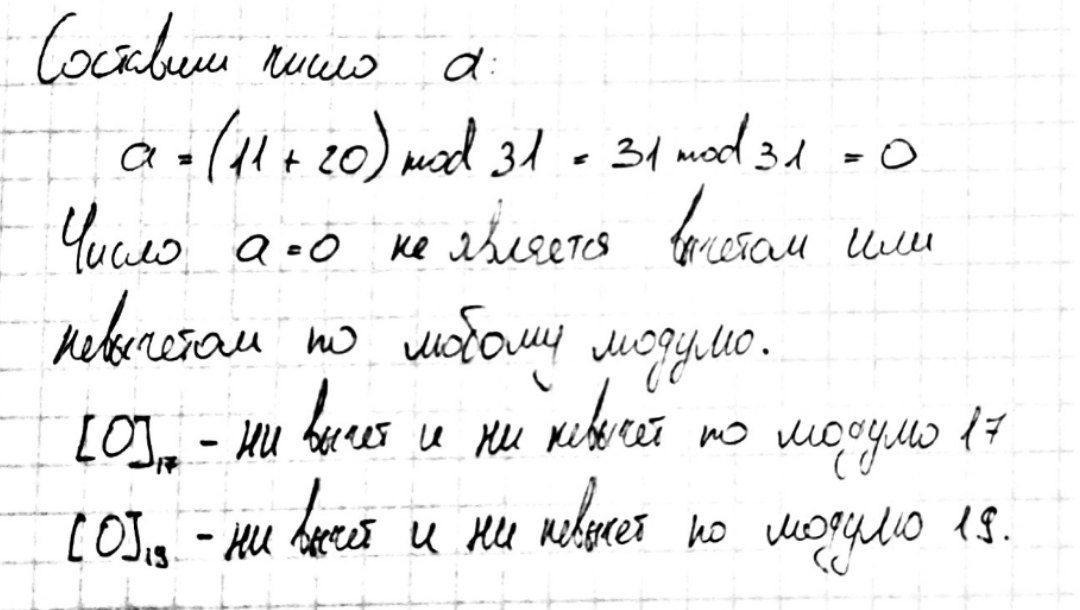
3. Решите уравнение .

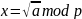N вар	Р=23	р=29
11	81	82

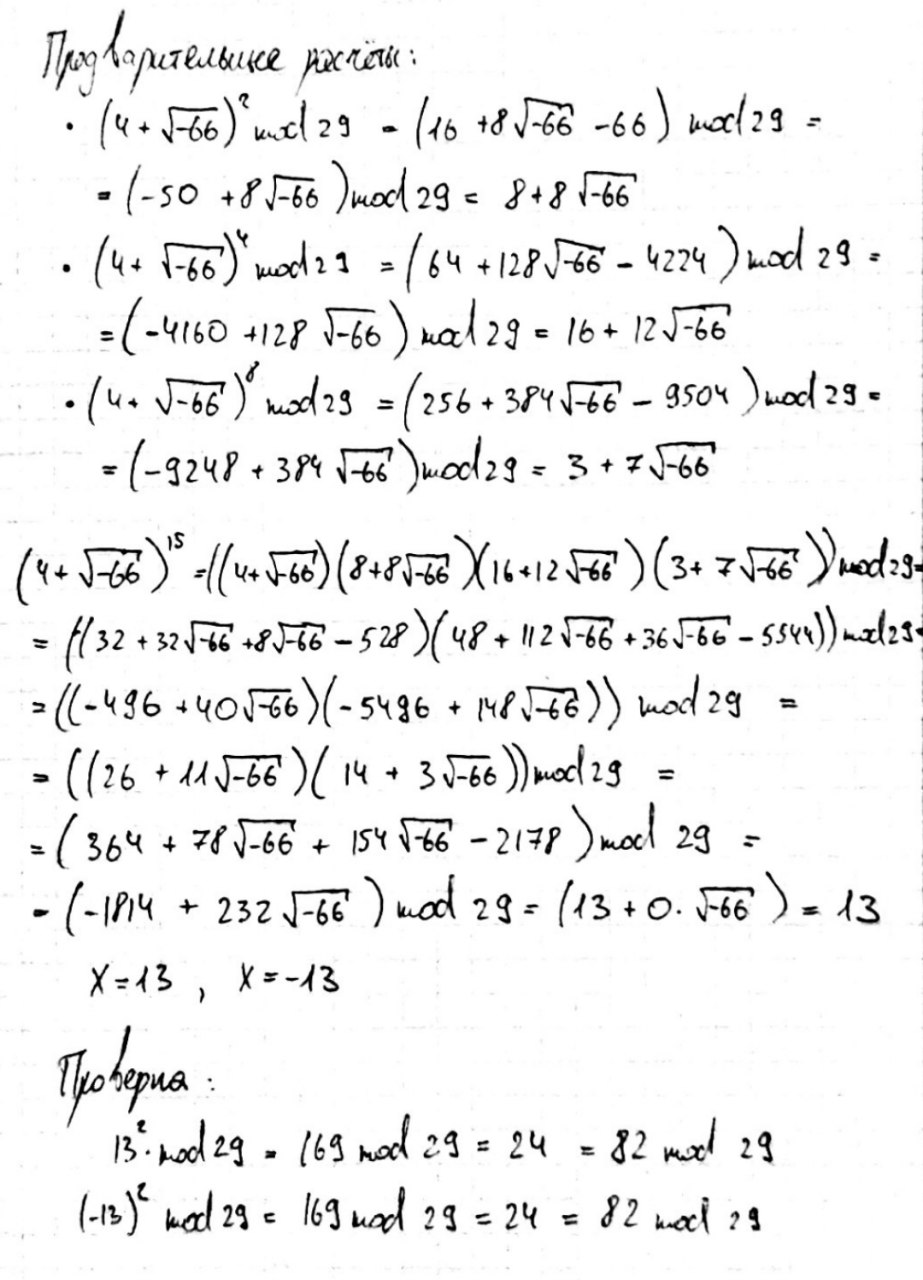
4. Решите все решения уравнение

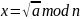
Для n=3*11, для вариантов 7-12, a=25

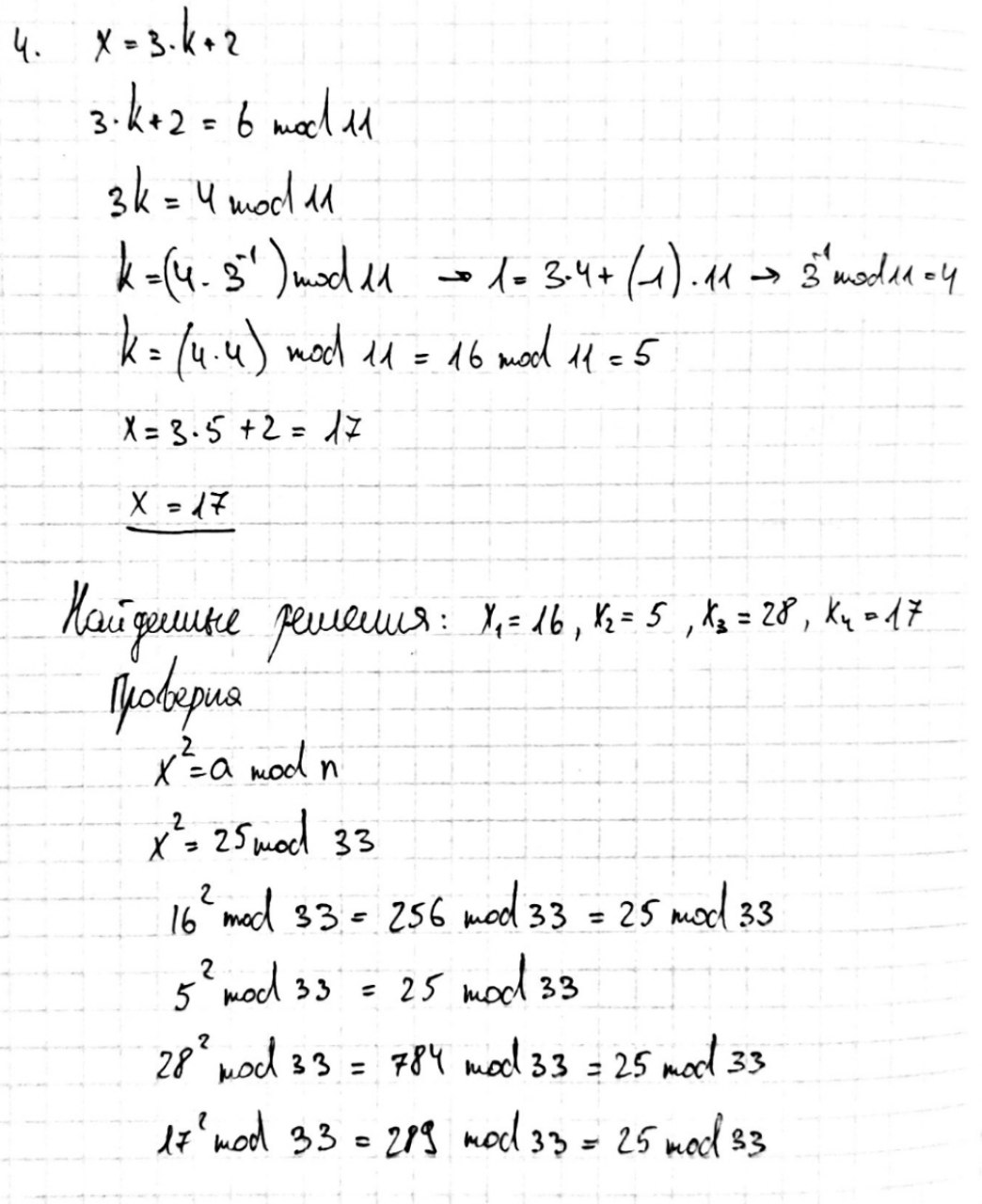
Вывод:

В ходе выполнения лабораторной работы провели тестирование простых чисел с помощью теста Ферма и теста Миллера-Рабина. Удалось установить, что тест Миллера-Рабина более эффективен, на примере чисел Кармайкла. Во второй части работы нашли квадратичные вычеты и не вычеты, решили несколько предложенных уравнений. Проверки показали, что решение уравнений выполнено верно.

Санкт-Петербург 2023 г