Лабораторная работа №1

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА» (СПбГУТ)

Факультет Инфокоммуникационных сетей и систем Кафедра Защищенных систем связи

Дисциплина Криптографические протоколы

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №1

Основы теории чисел

(тема отчета)

Информационная безопасность (10.03.01)

(код и наименование направления/специальности)

Студент группы ИКБ-06:

Ерохин А.Г.

(Ф.И.О.) (подпись)

Д.т.н., проф. каф. ЗСС:

Яковлев В.А.

(Ф.И.О.) (подпись)

Цель работы:

Закрепить знания, полученные на лекциях дисциплин «Криптографические методы защиты информации», «Криптографические протоколы» и приобрести навыки вычислений по блоку занятий «Математический базис криптосистем с открытым ключем».

Используемое программное обеспечение:

Для работы используется программа “Maxima” и дополнительные командные строки для решения каждой из задач.

Ход работы:

1. Перейти к пакету “Maxima”(M), выбрав в нем функцию integerp. Задавшись не менее, чем тремя произвольными пятиразрядными числами n и d проверить, являются ли числа d делителями n, используя следующие команды: integerp(n/d) (рис.1).

Рисунок 1 – Проверка делителей

2. Используя функцию divisors(n) в пакете (М) найти делители не менее чем трех пятиразрядных чисел при помощи следующей команды: divisors(n) (рис.2).

Рисунок 2 – Нахождение делителей

Убедиться в правильности расчетов “вручную”.

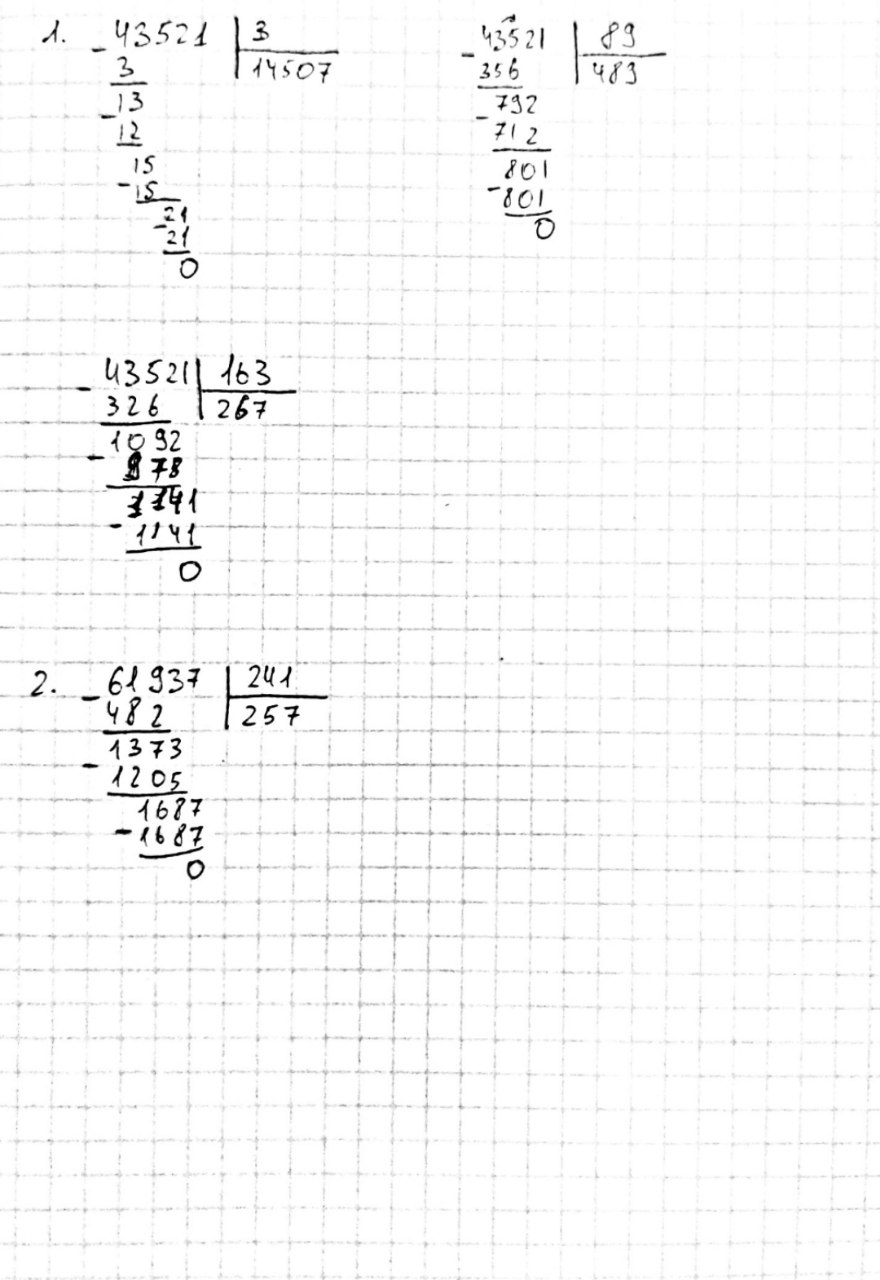
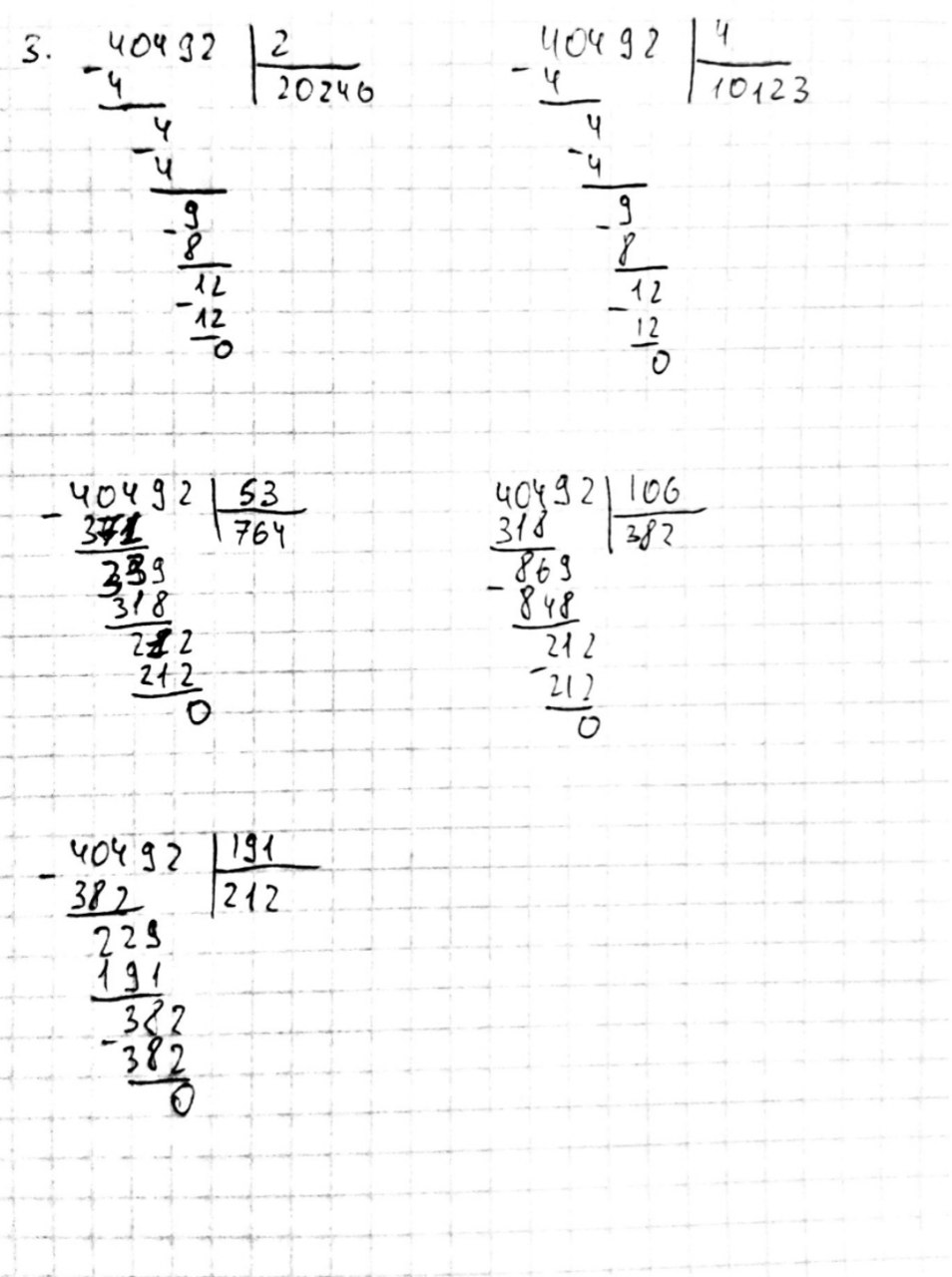
3. Используя функцию gcd(a,b) пакета (М) найти gcd одной пары четырех разрядных чисел и не менее чем четырех пар пятизначных чисел, одна из которых соответствует взаимно простым числам, при помощи следующей команды: gcd(a,b) (рис.3).

Рисунок 3 – Нахождение НОД

Убедиться в правильности расчетов “вручную” (на бумаге), выполнив следующее задание:

Найти наибольший общий делитель для пары чисел.

Четные номера. Найти НОД(8888,24NN),

Нечетные номера. Найти НОД(4848,12(NN+1)),

Решение:

Так как вариант – 11, следовательно НОД(4848,1212).

НОД(4848,1212) = 1212*НОД(4,1) = 1212 * 1 = 1212

Решение «вручную» совпадает с программным решением, следовательно расчёты выполнены верно.

4. Для найденных в п.3 пяти gcd(a,b), найти их канонические представления при помощи расширенного алгоритма Евклида при помощи следующей команды: gcdex(a,b) (рис.4).

Рисунок 4 – Расширенный алгоритм Евклида

Проверить правильность канонических представлений для всех случаев:

1. 4848*0 + 1212*1 = 1212 * 1 = 1212

2. 43521*(-20933) + 85454*10661 = -911025093 + 911025094 = 1

3. 61938*6002 + 14375*(-25861) = 371751876 – 371751875 = 1

4. 40492*(-1) + 10124*4 = -40492 + 40496 = 4

5. 15235*6 + 91405*(-1) = 91410 – 91405 = 5

5. Для одного четырехразрядного числа и не менее чем для четырех произвольно выбранных пятизначных чисел a сделать их приведение по модулям произвольных меньших чисел m при помощи команды: mod(a,m) (рис.5).

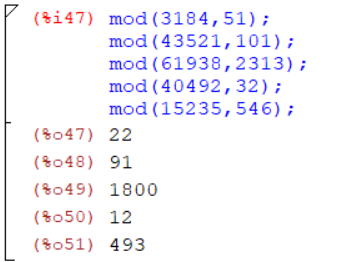
Рисунок 5 – Расчёт остатков от деления

Убедиться в правильности расчетов для первого числа “вручную”.

3184. mod 51 = (51*62 + 22) mod 51 = 22 mod 51 = 22

6. Найти мультипликативно обратные элементы к одному двухразрядному числу и не менее чем к четырем 9-ти значным числам a по простым двузначным модулям m при помощи следующей команды: power_mod(a,-1,m) (рис.6).

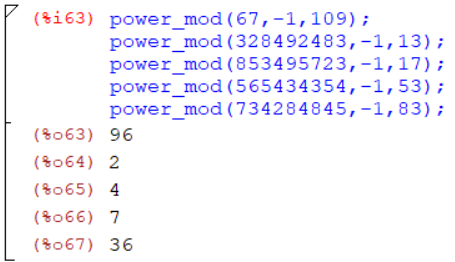
Рисунок 6 – Расчёт обратного элемента по модулю

Убедиться в правильности расчетов “вручную”, выполнив следующее задание:

Найти обратный элемент к числу а по mod b, где a соответствует числу в таблице 1, порядковый номер которого совпадает с Вашим номером по журналу, b с номером большим на 10 порядковый номер числа а.

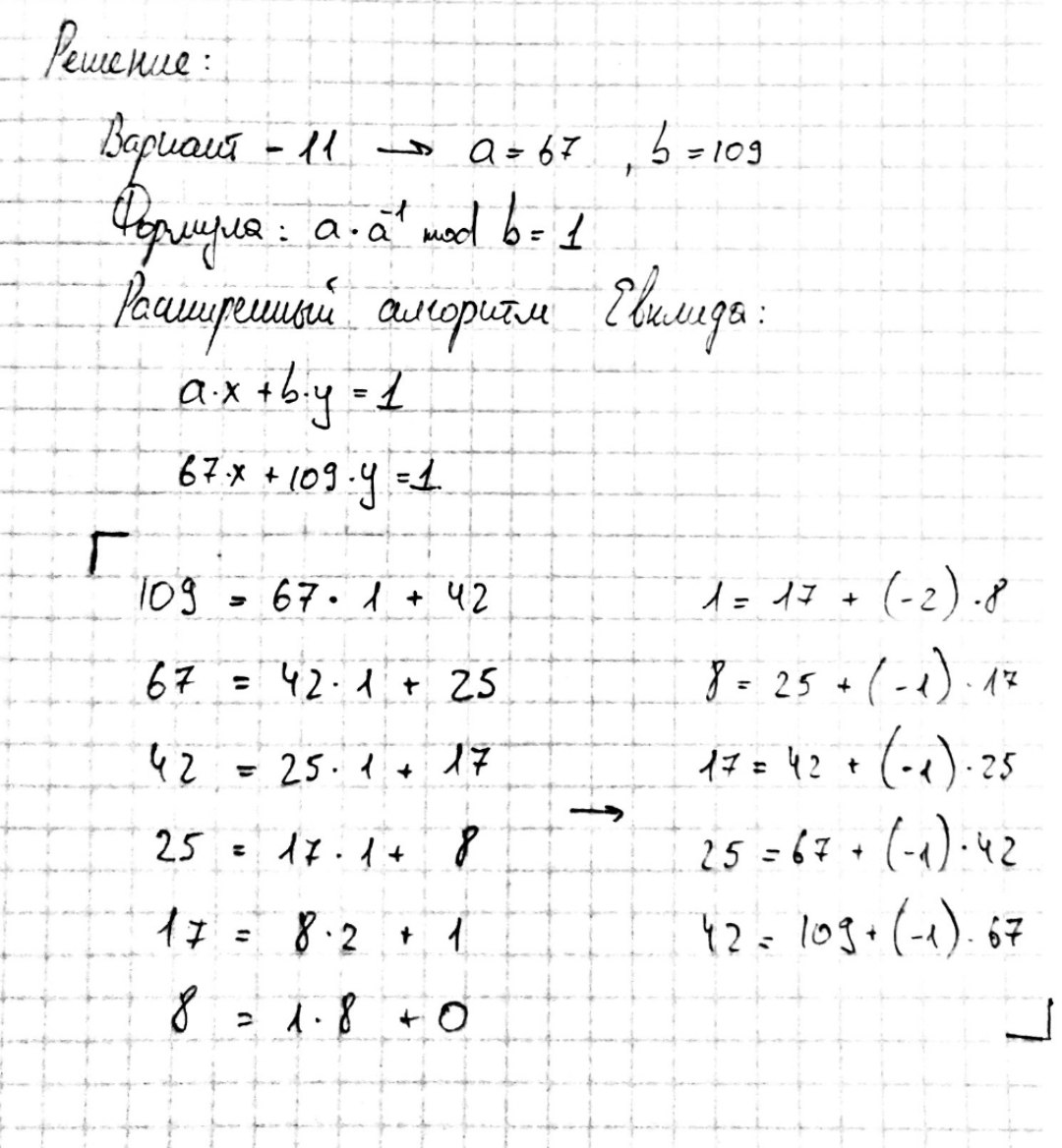
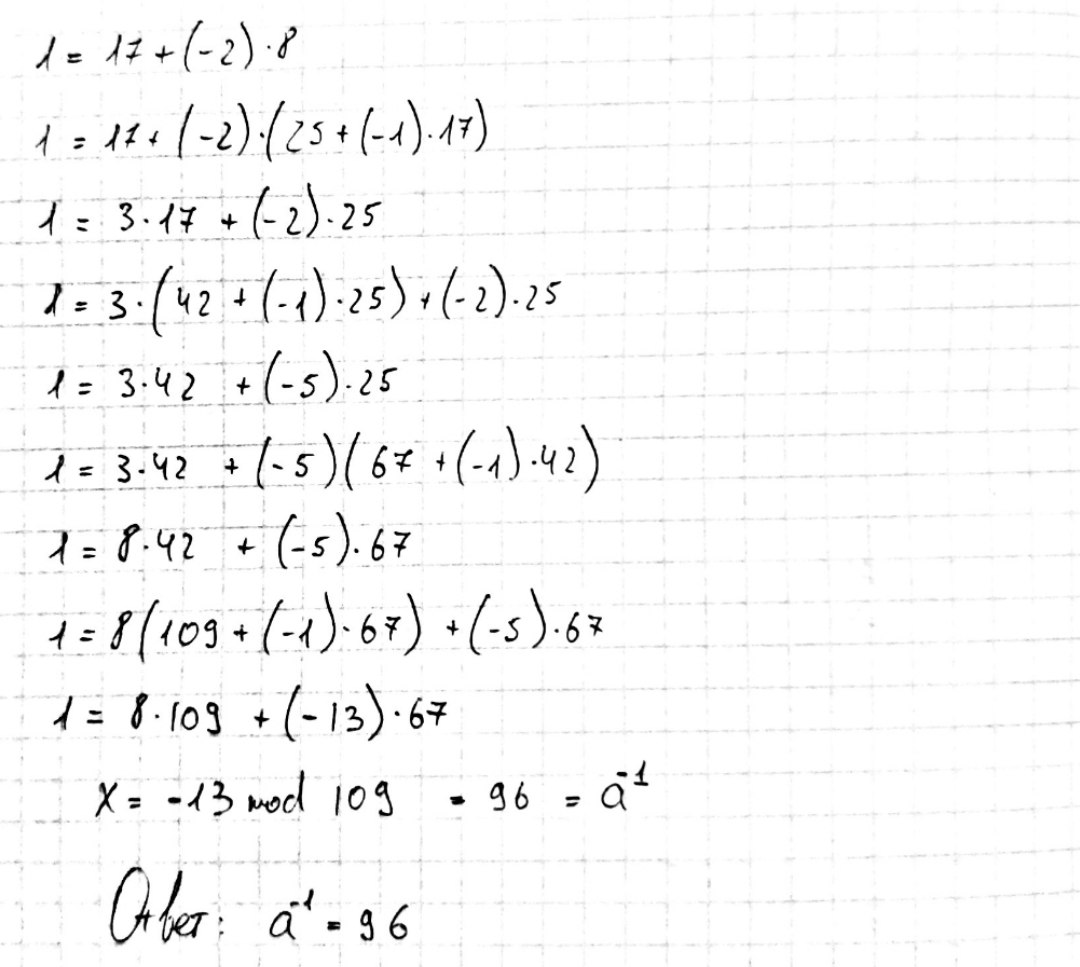
7. Рассчитать функцию Эйлера для одного двухразрядного числа не менее чем четырех четырехзначных чисел m, используя команду: totient(m) (рис.7).

Рисунок 7 – Расчёт функции Эйлера

Убедиться в правильности расчетов для первого числа “вручную”.

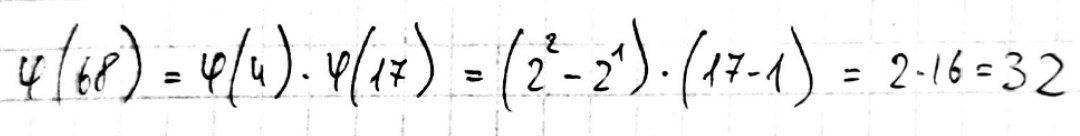
8. Для двух пар произвольных четырехзначных, но взаимно простых чисел a и m, проверить справедливость теоремы Эйлера при помощи следующей команды: mod(a^ totient(m),m) (рис.8).

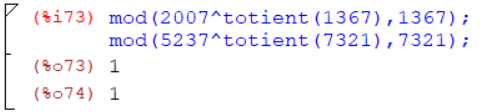
Рисунок 8 – Проверка справедливости теоремы Эйлера

9. Произвести возведение 5-значного произвольного числa в степень произвольного 15-значного числа b по произвольному 4-х значному модулю m, используя команду: power_mod(a,b,m) (рис.9).

Рисунок 9 – Вычисление алгоритмом быстрого возведения в степень

Используя алгоритм быстрого возведения в степень, вычислить вручную:

Четные номера. 3^1NN(mod7).

Нечетные номера. 5^1NN(mod7).

10. Решить систему уравнений на основе использования китайской теоремы об остатках.

,

где заданы таблицей

№ вар	ai	mi
11	5,7,8	17,11,9

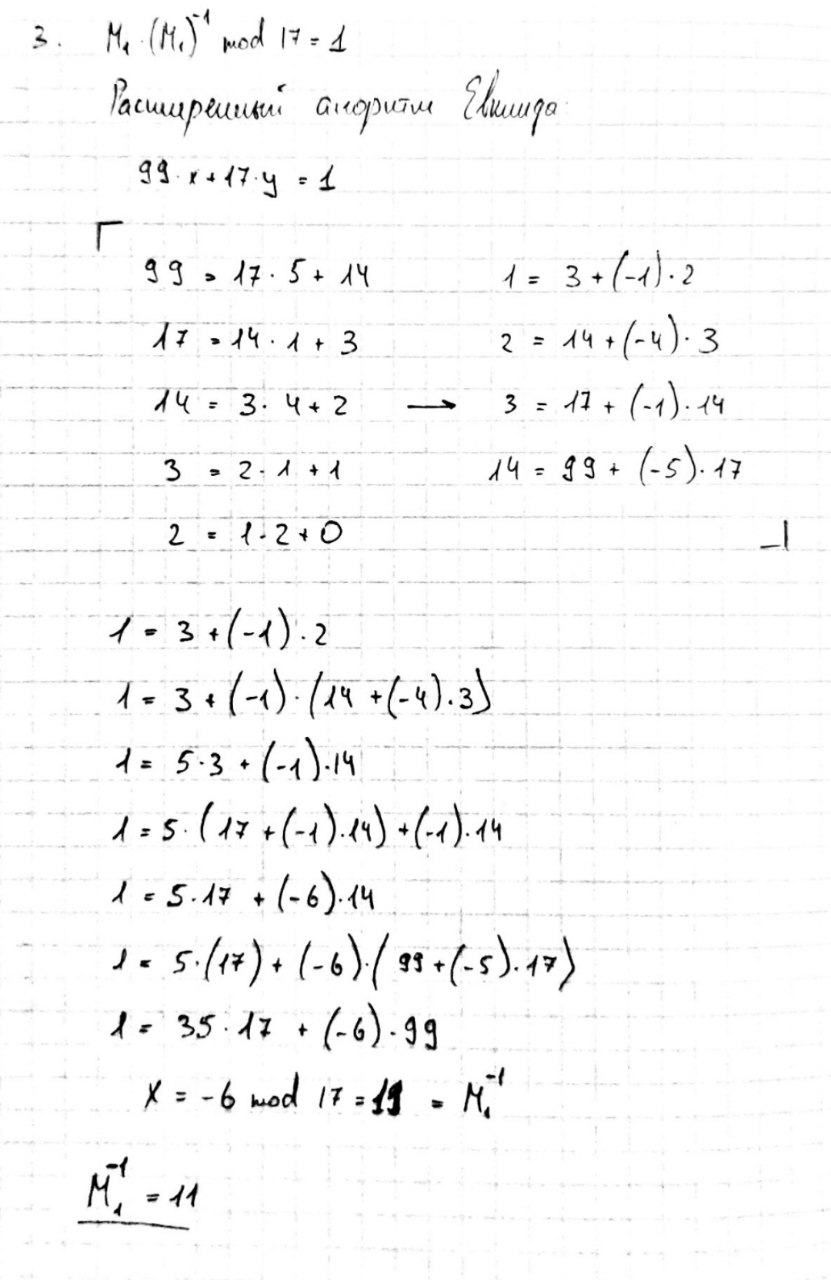
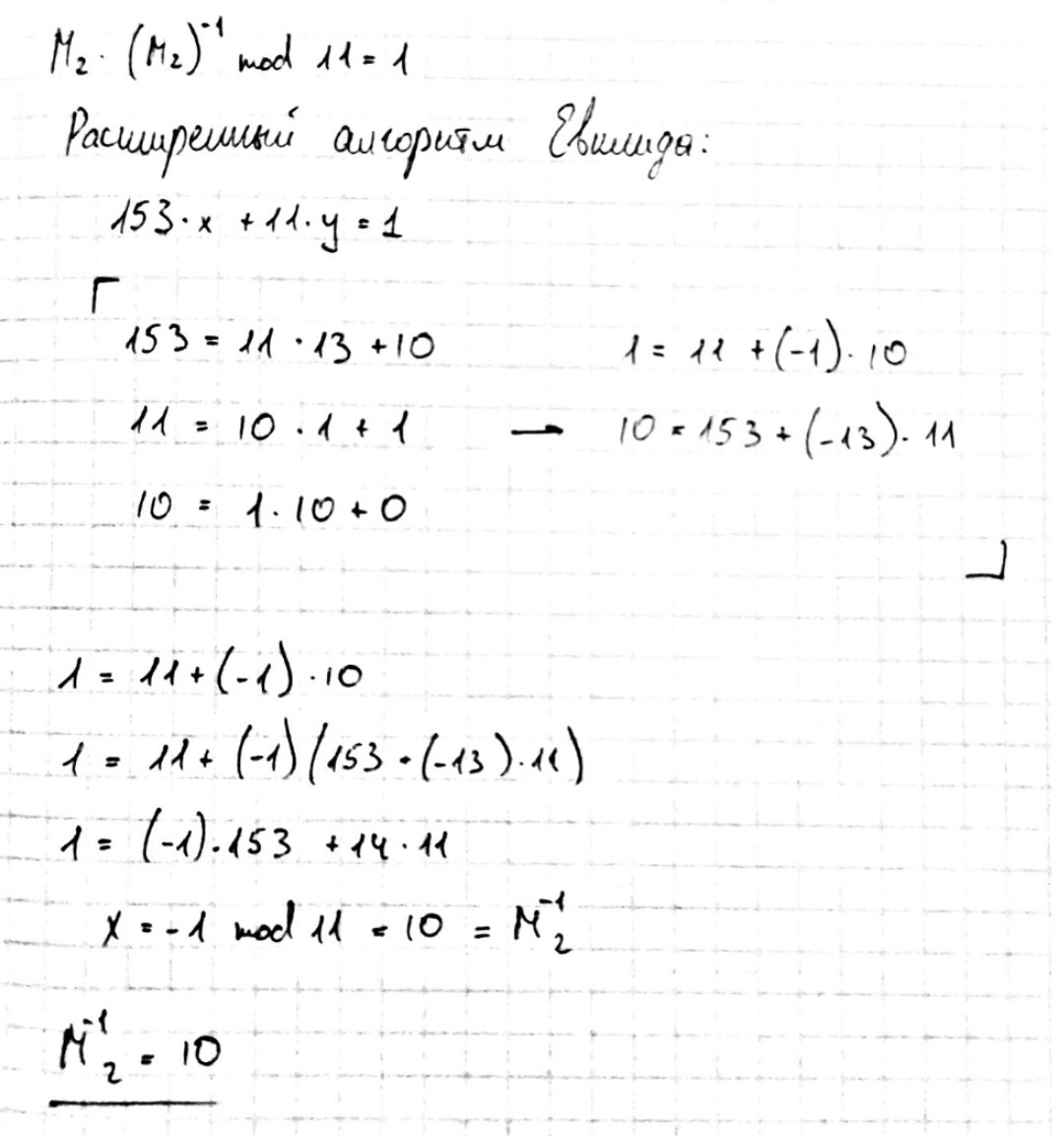
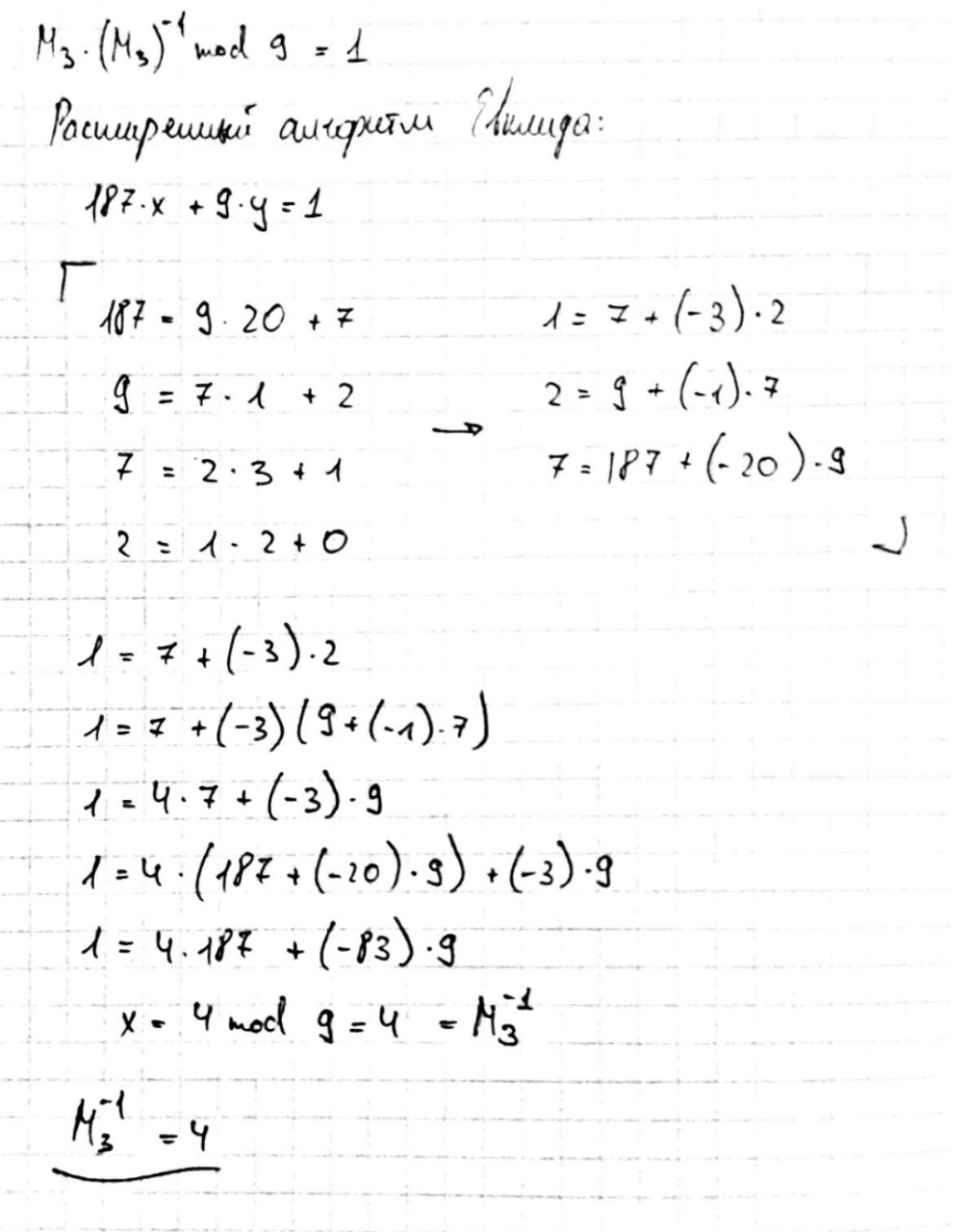
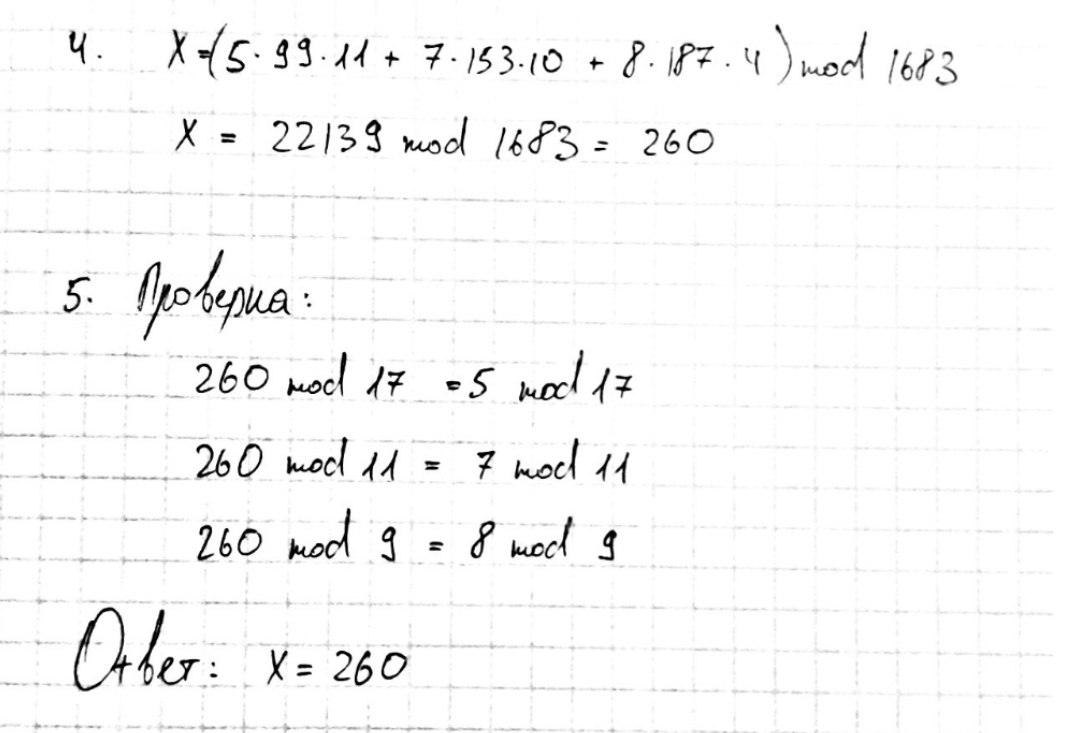
11. Разложите в цепную дробь числа: P/Q. Найдите подходящие дроби для k=1,2,3,4.

№ вар	P	Q
11	3885	2306

Цепная дробь: [1,1,2,5,1,4,2,3,3]

12. Решить контрольный пример.

, где

k=37,

а=№вар+11.

Примечание. Если получаетcя b=а, положить b=25.

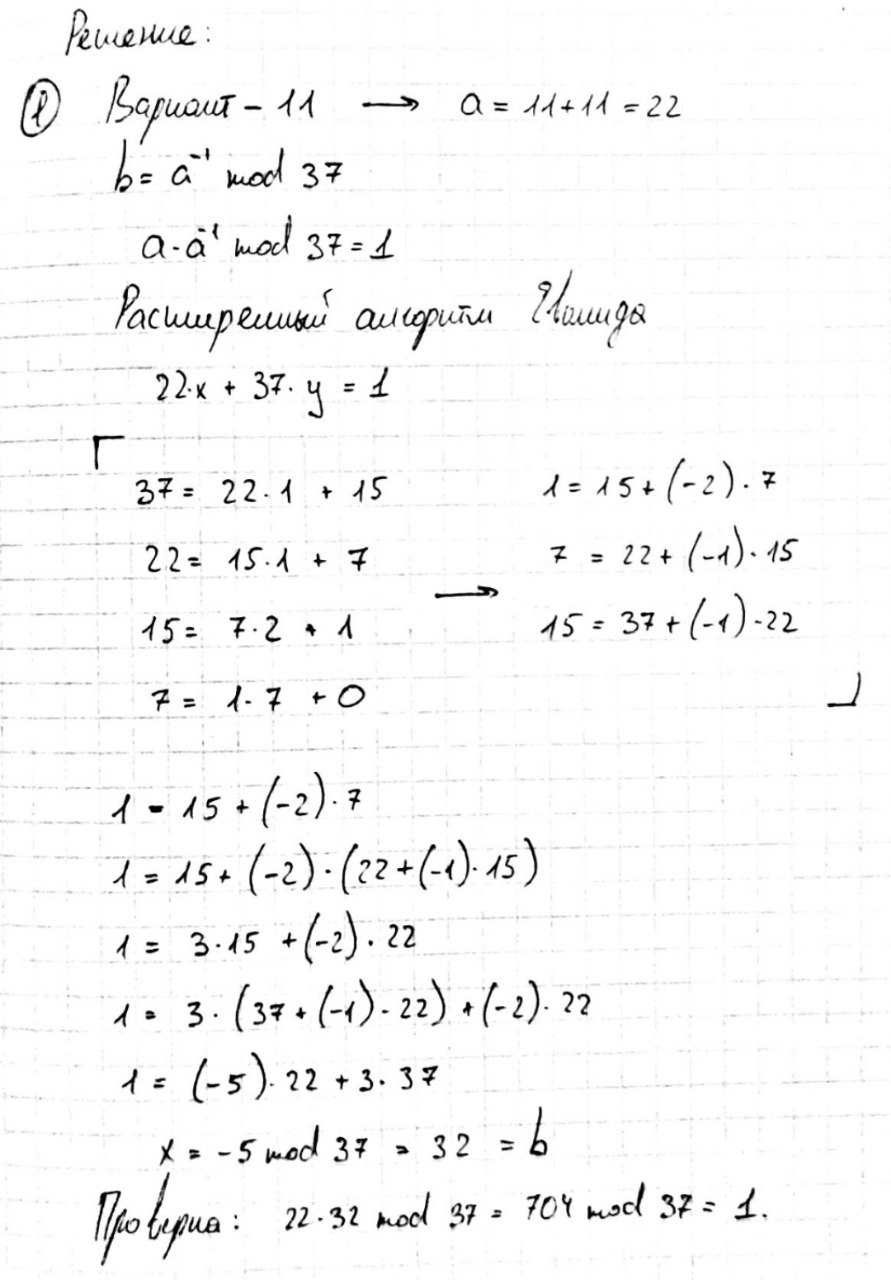
Вывод:

В ходе лабораторной работы закрепили практические навыки теории чисел. С помощью программы Maxima проводили вычисления таких элементов как: НОД, остаток от деления, функция Эйлера, алгоритм быстрого возведения в степень. Полученные результаты работы программы были полностью совпадают с «ручными» вычислениями. Была освоена китайская теорема об остатках и на её основе решено уравнение. В заключительной части работы закрепили ранее полученные навыки решением контрольного примера.

Санкт-Петербург 2023 г