Лабораторная работа №0

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА» (СПбГУТ)

Факультет Инфокоммуникационных сетей и систем Кафедра Защищенных систем связи

Дисциплина Криптографические протоколы

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №0

Исследование криптосистем с открытым ключом на основе эллиптических кривых

(тема отчета)

Информационная безопасность (10.03.01)

(код и наименование направления/специальности)

Студент группы ИКБ-06:

Ерохин А.Г.

(Ф.И.О.) (подпись)

Д.т.н., проф. каф. ЗСС:

Яковлев В.А.

(Ф.И.О.) (подпись)

Цель работы:

Приобретение навыков вычислений с использованием мат аппарата эллиптических кривых. Моделирование алгоритмов криптосистем с открытыми ключами на основе эллиптических кривых и их анализ.

Ход работы:

Задание 1. Задана эллиптическая кривая Е13(1,1) в поле GF(13) по уравнению . Точки Е13(1,1) (без нулевой точки) представлены на рис.1.

Рисунок 1 – Точки и граф эллиптической кривой

1. Проанализировать расположение точек на графе, проверить, что указанные точки действительно принадлежат, заданной кривой (2-3 точки). Найти взаимно обратные точки.

Точка (4, 2) принадлежит кривой, если выполняется равенство :

= (4³+4+1) mod 13 = 69 mod 13 = 4

y² = 2² mod 13 = 4 mod 13 = 4

Точка (4, 2) принадлежит кривой т. к. y² = = 4

Координаты взаимно обратной точки: (4, -2 mod 13) = (4, 11)

Точка (8, 12) принадлежит кривой, если выполняется равенство :

= (8³+8+1) mod 13 = 521 mod 13 = 1

y² = 12² mod 13 = 144 mod 13 = 1

Точка (8, 12) принадлежит кривой т. к. y² = = 1

Координаты взаимно обратной точки: (8, -12 mod 13) = (8, 1)

2. Выполнить вручную следующие вычисления:

• Найти точку С равную сумме двух точек , координаты точек и соответствуют вашему варианту задания.

• Найти противоположную точку .

• Вычислить точку , где k число согласно варианту задания.

Задание выполняется согласно варианту 11.

Таблица 1 – Исходные данные

	Задано				Найти
Nвар	A	B	k	C		-C	E=kC
11	8, 12	5, 1	4	12, 8		12, 5	4, 11

Решение:

1. Найдем точку C по формуле

Так как A≠B, то:

Для поиска обратного элемента воспользуемся расширенным алгоритмом Евклида: a * a^-1 mod b = 1.

1	=	10	+	(-3)	*	3
3	=	13	+	(-1)	*	10

a*x + b*y = 1

10*x + 13*y = 1

a		b		q		R
13	=	10	*	1	+	3
10	=	3	*	3	+	1
3	=	3	*	1	+	0

1 = 10 + (-3)*3

1 = 10 + (-3)*(13 + (-1)*10)

1 = 10 + (-3)*13 + 3*10

1 = 4* 10 + (-3) * 13

a^-1 = 4

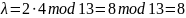
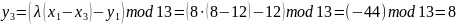
Координаты точки С(12, 8)

2. Поиск противоположной точки C

3. Вычисление точки E=kC, k = 4

• 

Так как С = С, то:

Для поиска обратного элемента воспользуемся расширенным алгоритмом Евклида: a * a^-1 mod b = 1.

1	=	13	+	(-4)	*	3
3	=	16	+	(-1)	*	13

a*x + b*y = 1

16*x + 13*y = 1

a		b		q		R
16	=	13	*	1	+	3
13	=	3	*	4	+	1
3	=	3	*	1	+	0

1 = 13 + (-4)*3

1 = 13 + (-4)*(16 + (-1)*13)

1 = 13 + (-4)*16 + 4*13

1 = (-4) * 16 + (5) * 13

a^-1 = -4 mod 13 = 9

2C = D(11, 2)

• 

Так как D = D, то:

В пункте 1 мы находили обратный элемент по модулю от числа 10 и получили, что 10^-1 = 4 mod 13 = 4. Следовательно 10 и 4 обратные элементы по модулю 13. Получаем 4^-1 = 10 mod 13 = 10.

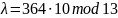
2D = E(4, 11)

• 

Задание 2. Моделирование криптосистемы Эль-Гамаля на эллиптической кривой. Задана кривая Е67(2, N), где N номер варианта. Записать ее уравнение. Задание выполняется согласно варианту 11.

Таблица 2 – Параметры криптосистемы

	Задано			Вычислить
Nвар	d	r	E1		E2	C1	C2
11	3	4	7, 10		59, 32	10, 48	2, 31

Решение:

Уравнение имеет вид:

Рисунок 2 – Поиск точек эллиптической кривой

Генерирование ключей (корреспондент А):

• Выбрать произвольную точку 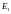с координатами (x, y).

Выбрали точку (7, 10).

• Проверить принадлежит ли точка кривой (проверку записать в отчет).

Точка принадлежит эллиптической кривой, если выполняется равенство: .

= (7³+2*7+11) mod 67 = 368 mod 67 = 33

y² = 10² mod 67 = 100 mod 67 = 33

Точка (7, 10) принадлежит кривой т. к. y² = = 33

• Выбрать целое число d, согласно варианту задания.

Согласно варианту d = 3 (закрытый ключ).

• Вычислить точку , используя алгоритм быстрого вычисления.

Рисунок 3 – Вычисление E₂

• Параметры: ЭК Е67(2, N), , передать корреспонденту В, в качестве открытого ключа, параметр d-закрытый ключ (не передается).

Открытый ключ:

Шифрование сообщения (корреспондент В):

• Выбрать сообщение в виде произвольной точки ЭК P(x, y).

P(x, y) = (60, 18)

• Выбрать случайное число r;

r = 4

• Вычислить криптограмму в виде пары точек:

Рисунок 4 – Вычисление С₁

Рисунок 5 – Вычисление С₂

• Передать С1 и С2 корреспонденту А.

Передано: ,

Расшифрование криптограммы (корреспондент А):

• Получить криптограмму: С1 и С2

Полученная криптограмма: ,

• Найти переданное сообщение по формуле , где знак минус означает сложение с противоположным элементом к точке .

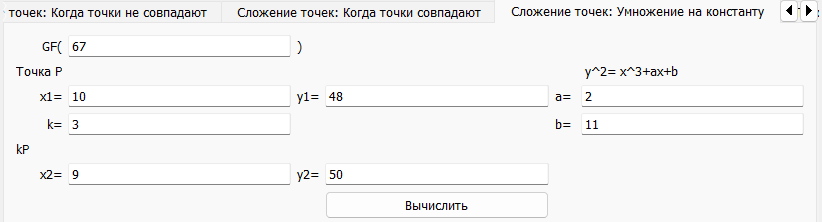
Рисунок 6 – Вычисление

(9, 50)

Противоположный элемент к точке : (9, (-50) mod 67) = (9, 17)

Рисунок 7 – Вычисление P

Расшифрованное сообщение Р имеет координаты (60, 18), которые совпадают с координатами P до шифрования, что свидетельствует о правильном результате дешифрования криптограммы.

Вывод:

В ходе выполнения лабораторной работы были приобретены навыки анализа алгоритмов криптосистем с открытыми ключами на основе эллиптических кривых. В процессе выполнения работы было произведено генерирование корреспондентом А открытого и закрытого ключей. Открытый ключ был передан корреспонденту В, на основе которого производилось шифрование сообщения P. Криптограмма в виде пары точек была передана корреспонденту А, для дешифрования закрытым ключом. В результате дешифрования получили, что полученное сообщение и передаваемое совпадают, что говорит о правильности проведенного дешифрования.

Санкт-Петербург 2023 г