
Matematikaliq analiz oqiw qollanba
.pdfboladı. f (x) C [a, b] bolıwınan k → + |
da f (x' |
) → f (x |
0 |
), |
f (x' ' |
) → f (x |
0 |
) bolıp, |
|||
|
|
n |
k |
|
|
n |
k |
|
|
||
|
|
|
|
|
|
|
|
|
|
||
olardan k → + de f (x' |
) − f (x' ' ) → 0 |
kelip shıǵadı. Bul bolsa |
n N ushın |
||||||||
nk |
nk |
|
|
|
|
|
|
|
|
|
|
|
| f (x' ) − f (x |
' ' ) | |
|
|
|
|
|
|
|
|
|
|
|
n |
n |
|
|
|
|
|
|
|
|
dep alınǵanǵa qarama-qarsı keledi. Demek, f (x) funkciya [a, b] da teń ólshewli úzliksiz boladı. ►
80

6-§. FUNKCIYANIŃ TUWINDISI HÁM DIFFERENCIALLARI
6.1. Funkciyanıń tuwındısı. Funkciya tuwındısınıń geometriyalıq hám mexanikalıq mánisleri
Meyli |
f (x) |
funkciya |
(a,b ) R |
da |
berilgen |
bolıp, |
x0 (a,b ), x0 |
+ x (a,b ) bolsın. |
f (x0 )= f (x0 |
+ x)− f (x0 ) ayırma |
f (x) |
||
funkciyanıń x0 |
tochkadaǵı ósimi delinedi. |
|
|
|
||
1-anıqlama. Eger
|
|
|
|
|
lim |
f (x0 + x) − f (x0 ) |
|
|||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|||
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|||
limit bar hám shekli |
bolsa, |
onda |
f (x) funkciyanıń x0 tochkadaǵı tuwındısı |
|||||||||||
delinedi hám |
df (x0 ) |
|
f ( x0 ) yamasa ( f (x)) x |
kórinisinde belgilenedi. Demek, |
||||||||||
dx |
||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
f (x |
|
) = lim |
f (x0 + x) − f (x0 ) |
. |
|
(1) |
|||||
|
|
|
0 |
|
||||||||||
|
|
|
|
x→0 |
x |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||
Eger x0 + x = x bolsa, onda x = x − x0 |
hám x → 0 da x → x0 |
bolıp, (1) |
||||||||||||
qatnas tómendegi |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
f (x0 ) = |
lim |
f (x) − f (x0 ) |
|
(2) |
||||
|
|
|
|
|
|
x − x |
||||||||
|
|
|
|
|
|
|
|
x→x0 |
|
|||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|||
kóriniske keledi.
1-mısal. f (x) = x, x0 R bolsın. Bul funkciya ushın
|
f (x) − f (x0 ) |
= |
x − x0 |
=1 |
||
|
x − x0 |
x − x0 |
||||
|
|
|
||||
bolıp, |
|
|
|
|
|
|
|
lim |
f (x) − f (x0 ) |
=1 |
|||
|
x − x |
|
||||
|
x→x0 |
|
|
|
||
0
boladı. Demek, f (x) = (x) =1.
2-mısal. f (x)= x , x R bolsın.
81
|
x 0 |
|
|
|
|
f (x)= x |
|
|
|
|
|
|
f (x) =1 |
|
|
|
|
|
|
|
|||||
Eger |
|
bolsa, onda |
|
|
|
|
|
bolıp, |
|
|
|
|
|
boladı. |
|
|
|||||||||
|
x 0 |
|
|
|
f (x)= −x |
|
|
|
|
f (x) = −1 |
|
|
|
|
|
|
|||||||||
Eger |
|
bolsa, onda |
|
|
|
|
|
|
bolıp, |
|
|
|
|
|
boladı. |
|
|
||||||||
Eger |
x = 0 bolsa, onda |
f (x) − 0 |
= |
| x | |
|
|
bolıp, x → 0 da bul qatnaslardıń limiti |
||||||||||||||||||
|
|
||||||||||||||||||||||||
|
0 |
|
|
|
|
|
x − 0 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
bolmaydı. Demek, berilgen funkciya |
x0 = 0 tochkada tuwındıǵa iye bolmaydı. |
||||||||||||||||||||||||
|
Funkciyanıń oń |
|
hám |
|
shep |
tuwındıları. Meyli f (x) |
funkciya |
X R |
|||||||||||||||||
kóplikte berilgen bolıp, (x0 − , |
|
|
x0 ) X |
( 0) bolsın. |
|
|
|||||||||||||||||||
|
2-anıqlama. Eger |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
f (x) − f (x0 ) |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x − x |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
x→x0 −0 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
limit bar bolsa, bul limit |
f (x) funkciyanıń x0 tochkadaǵı shep tuwındısı delinedi |
||||||||||||||||||||||||
hám |
f (x0 − 0) kórinisinde belgilenedi: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
f |
(x |
|
− 0) = |
|
|
lim |
f (x) − f (x0 ) |
. |
|
|
||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→x0 −0 |
|
x − x |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
Meyli |
f (x) funkciya |
X R kóplikte berilgen bolıp, |
(x0 , x0 + ) X |
|||||||||||||||||||||
( 0) bolsın. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
3-anıqlama. Eger |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
f (x) − f (x0 ) |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x − x |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
x→x0 |
+0 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
limit bar bolsa, onda bul limit |
f (x) funkciyanıń x0 tochkadaǵı oń tuwındısı |
||||||||||||||||||||||||
delinedi hám |
f (x0 + 0) kórinisinde belgilenedi: |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
f |
(x |
|
+ 0) = |
|
|
lim |
f (x) − f (x0 ) |
. |
|
|
||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→x0 + 0 |
|
x − x |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
Máselen, |
f (x) =| x | funkciyanıń x0 |
= 0 tochkadaǵı oń tuwındısı f (+0) =1, |
||||||||||||||||||||||
shep tuwındısı |
f (−0) = −1 boladı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Funkciya tuwındısınıń geometriyalıq hám mexanikalıq mánisleri. |
Meyli |
|||||||||||||||||||||||
f (x) funkciya (a,b ) da berilgen bolıp, |
x0 (a,b ) tochkada |
f '(x0 ) tuwındıga |
|||||||||||||||||||||||
82
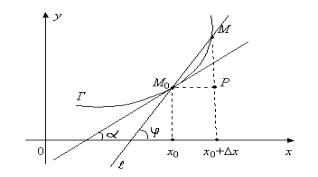
iye bolsın. Bul f (x) funkciyanıń grafigi 5-sızılmada súwretlengen Г iymek sızıqtı
belgileymiz:
5-sızılma.
Bul Г sızıqta M0 ( x0 , y0 ), M ( x, y ) tochkalardı alıp, olar arqalı ótiwshi l tuwrı sızıǵın qaraymız.
M0 ( x0 , f (x0 )) Г , M ( x, f (x)) Г , M → M0 da l tuwrı sızıqtıń limit jaǵdayı Г sızıqqa M 0 tochkada ótkizilgen urınba delinedi.
Bunnan, múyesh x qa baylanıslı, = ( x) hám f (x) funkciyanıń grafigine M 0 tochkada ótkizilgen urınbanıń bar bolıwı ushın
lim ( x) =
x→0
teńliktiń orınlanıwı lazım. Bunda – urınbanıń OX kósheriniń oń baǵdarı menen payda bolǵan múyesh. M0 MP úshmúyeshlikten:
|
tg ( x) = |
MP |
= |
|
f (x0 + x) − f (x0 ) |
|
|
|||||||
|
M 0 P |
|
|
|
|
x |
|
|||||||
bolıp, onnan |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( x) = arctg |
|
f (x0 + x) − f (x0 ) |
|
|
|||||||||
|
|
|
|
|
|
|
x |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
kelip shıǵadı. Funkciya úzliksizliginen paydalanıp, |
|
|||||||||||||
|
lim ( x) = lim arctg |
|
f (x0 |
+ x) − f (x0 ) |
= |
|||||||||
|
|
|
|
x |
||||||||||
|
x→0 |
x→0 |
|
|
|
|
|
|
|
|
||||
|
|
f (x0 + x) − f (x0 ) |
|
|||||||||||
|
= arctg lim |
|
|
|
|
|
|
|
|
|
= arctgf (x0 ). |
|||
|
|
|
|
x |
|
|
|
|
||||||
|
x→0 |
|
|
|
|
|
|
|
|
|
||||
Demek, x → 0 |
da ( x) niń limiti bar hám |
|
|
|
|
|
|
|||||||
83
= arctgf (x0 ) .
Keyingi teńlikten
|
|
|
|
|
|
f (x0 ) = tg |
|
|
|||||||
kelip shıǵadı. Demek, funkciyanıń x0 |
tochkadaǵı |
f '(x0 ) tuwındısı urınbanıń |
|||||||||||||
múyeshlik koefficentin belgileydi. Bunda urınbanıń teńlemesi |
|||||||||||||||
|
|
|
|
y = f (x0 ) + f (x0 )(x − x0 ) |
|||||||||||
kórinisinde boladı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Meyli P tochka tuwrı sızıq boylap |
s = s(t) |
nızam menen háreket qılsın, |
|||||||||||||
bunda t −waqıt, s −ótilgen jol. Eger waqıttıń t1 |
hám |
t2 (t1 t2 ) mánislerindegi |
|||||||||||||
ótilgen jol s(t1 ), |
s(t2 ) bolsa, onda bul qatnas |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
s(t2 ) − s(t1 ) |
|
|
|||||||
|
|
|
|
|
|
|
t2 − t1 |
|
|
|
|
|
|||
[t1 , t2 ] waqıt aralıǵındaǵı ortasha tezlikti ańlatadı. |
|
|
|||||||||||||
Tómendegi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
s(t2 ) − s(t1 ) |
|
|
||||||
|
|
|
|
|
|
t |
|
− t |
|
|
|||||
|
|
|
|
|
t2 →t1 +0 |
2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||
limit háreketdegi tochkanıń t1 waqıttaǵı tezligin bildiredi. |
|||||||||||||||
Demek, hárekettegi P tochkanıń t |
waqıttaǵı tezligi v(t) , óttilgen s(t) joldıń |
||||||||||||||
tuwındısınan ibarat boladı: |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
v(t) = s (t). |
|
|
|||||||
Meyli f (x) funkciya (a, b) R da berilgen bolsın. |
|||||||||||||||
Teorema. Eger f (x) funkciya x0 (a, b) |
|
tochkada shekli f (x0 ) tuwındıǵa |
|||||||||||||
iye bolsa, onda |
f (x) |
funkciya x0 |
tochkada úzliksiz boladı. |
||||||||||||
◄ Meyli |
f (x) |
funkciya x0 (a, b) tochkada shekli f (x0 ) tuwındıǵa iye |
|||||||||||||
bolsın. Anıqlamaǵa tiykarlanıp |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
f (x |
|
) = lim f (x0 ) |
= lim |
|
f (x0 + x) − f (x0 ) |
||||||||
|
|
0 |
|
|
|
|
|
||||||||
|
|
|
x→0 |
x |
x→0 |
x |
|||||||||
|
|
|
|
||||||||||||
yamasa
84
x → 0 da f (x0 ) → f (x0 )
x
boladı. Endi = f (x0 ) − f (x0 ) dep belgilemiz. Bunnan x → 0 da → 0.
x
Keyingi teńliklerden
f (x0 ) = f (x0 ) x + x.
Ádette, bul teńlik funkciya ósiminiń formulası delinedi. Onnan
lim f (x0 ) = 0
x→0
kelip shıǵadı. Bul f (x) funkciyanıń x0 tochkada úzliksiz ekenin bildiredi. ►
Eskertiw. Funkciyanıń bazı tochkada úzliksiz bolıwınan onıń usı tochkada shekli tuwındıǵa iye bolıwı hár dayım hám kelip shıǵa bermeydi. Máselen,
f (x) =| x | |
funkciya |
x = 0 tochkada úzliksiz, biraq usı tochkada tuwındıǵa iye |
|||||||||||
emes. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6.2. Tuwındını esaplaw qaǵıydaları hám formulaları |
|
||||||||||
Meyli f (x) |
hám g (x) funkciyaları (a,b ) R da berilgen |
bolıp, |
|||||||||||
x0 (a,b ) |
tochkada f (x0 ) hám |
g (x0 ) |
tuwındılarǵa iye bolsın. Tuwındınıń |
||||||||||
anıqlamasına muwapıq |
|
|
|
|
|
|
|
|
|
||||
|
|
|
lim |
f (x) − f (x0 ) |
= f (x |
|
), |
(1) |
|||||
|
|
|
|
|
0 |
||||||||
|
|
|
x→x0 |
x − x |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
lim |
g(x) − g(x0 ) |
= g (x |
|
) |
|
(2) |
||||
|
|
|
|
0 |
|
||||||||
|
|
|
x→x0 |
x − x |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
boladı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
1) |
f (x) g(x) funkciya x0 tochkada tuwındıǵa iye bolıp, |
|
|||||||||||
|
|
|
( f (x) g(x)) x |
= f (x0 ) g (x0 ) |
|
||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
boladı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
f (x) g(x) funkciya x0 tochkada tuwındıǵa iye bolıp, |
|
|||||||||||
|
|
|
( f (x) g(x)) x |
= f (x0 ) g(x0 ) f (x0 ) g (x0 ) |
|
||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
85
boladı. |
|
|
|
|
|
|
|
|
|
|
|
3) |
f (x) |
funkciya (g(x0 ) 0) |
x0 tochkada tuwındıǵa iye bolıp, |
||||||||
g(x) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
f (x) |
|
|
f (x0 ) g(x0 ) − f (x0 ) g (x0 ) |
|||||
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||
|
|
|
|
|
x0 |
g |
(x0 ) |
||||
|
|
g(x) |
|
|
|
||||||
boladı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
1-nátiyje. Eger |
f (x) funkciya x0 tochkada |
f (x0 ) tuwındıǵa iye bolsa, |
|||||||||||
onda c f (x) funkciya |
(c = const ) |
x0 tochkada tuwındıǵa iye bolıp, |
|
|
|||||||||
|
|
|
(c f (x)) x0 |
= c f (x0 ) |
|
|
|
|
|
||||
boladı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
2-nátiyje. Eger |
f1 (x), f2 (x), ..., |
|
fn (x) |
funkciyalar |
x0 |
tochkada |
|||||||
tuwındılarǵa iye bolıp, с1, с2 , ..., сn |
turaqlı sanlar bolsa, onda |
|
|
|
|
||||||||
|
|
|
|
|
|
|
' |
(x0 ) + ... + cn |
' |
(x0 ) |
|||
|
(c1 f1 (x) + c2 f 2 (x) + ... + cn f n (x)) x0 |
= c1 f1 |
(x0 ) + c2 f 2 |
f n |
|||||||||
boladı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Quramalı funkciyanıń tuwındısı. Meyli |
y = f (x) funkciya X R , g(y) |
||||||||||||
funkciya |
f (x) | x X |
kóplikte |
berilgen |
bolıp, |
x0 X |
tochkada |
f '(x0 ) |
||||||
tuwındıǵa, |
y0 f (x) | |
x X tochkada |
( y0 = f (x0 )) |
g (y0 ) |
tuwındıǵa iye |
||||||||
bolsın. Onda g( f (x)) quramalı funkciya x0 |
tochkada tuwındıǵa iye bolıp, |
||||||||||||
|
|
|
(g( f (x)))'x = g ( f (x0 )) f (x0 ) |
|
|
|
|
||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
boladı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Keri funkciyanıń tuwındısı. |
Meyli y = f (x) |
funkciya |
(a,b ) da berilgen, |
||||||||||
úzliksiz hám qatań ósiwshi (qatań kemeywshi) bolıp, x0 (a,b ) tochkada |
f '(x0 ) |
|||||||||
( f '(x |
0 |
) 0) tuwındıǵa iye bolsın. Onda |
x = f −1 ( y) funkciya y |
0 |
( y = f (x )) |
|||||
|
|
|
|
|
|
|
0 |
0 |
||
tochkada tuwındıǵa iye hám |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
f −1 |
( y) x0 |
= |
|
|
|
|
|
|
|
|
f (x0 ) |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||
boladı.
86
1-mısal. (x ) = x −1 boladı, bunda R , x 0 .
◄ Meyli x 0 bolsın. Onda f (x)= x funkciya ushın
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
x |
|
|
|
||||
|
|
(x + x) − x |
|
|
|
1 |
x |
|
−1 |
|
|
||||||||||
|
|
|
−1 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
= x |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
x |
|
|
|
|
|
x |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
bolıp, x → 0 da (x ) = x −1 |
boladı. ► |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2-mısal. (a x ) = a x ln a boladı, bunda a 0 , x R . |
|
|
|
|
|||||||||||||||||
◄ f (x) = a x funkciya ushın |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
a x+ x − a x |
|
= a x |
|
a x −1 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
x |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
||||||
bolıp, x → 0 da (a x ) = a x ln a boladı. ► |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
3-mısal. (sin x) = cos x , |
(cos x) = −sin x boladı, bul jerde x R . |
|
|||||||||||||||||||
◄ f (x)= sin x funkciya ushın |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
sin(x + x) − sin x |
= 2 |
1 |
sin x cos x + x |
= |
sin 2 |
cos x + |
x |
|||||||||||||
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|||
|
x |
|
x |
2 |
|
|
|
|
|
|
2 |
|
|
2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
bolıp, x → 0 da (sin x) = cos x boladı. Tap usıǵan uqsas (cos x) = −sin x bolıwı tabıladı.►
Tuwındılar kestesi. Tómende ápiwayı funkciyalardıń tuwındıların ańlatıwshı formulalardı keltiremiz:
1. (С)' = 0, C = const .
2. (x )'= x −1, R, x 0. (x n )'= nxn−1 , n N, x R.
3. (a x )'= a x ln a, a 0, a 1, x R
(e x )'= e x , x R.
87

4. |
(loga x)' = |
|
|
|
|
|
1 |
|
|
|
|
|
, |
|
|
|
|
|
a 0, |
a 1, x 0. |
||||||||||||||||
|
|
|
x ln a |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
(loga | x |)' |
= |
|
|
|
|
|
|
1 |
|
|
|
|
|
, |
|
|
|
|
|
a 0, |
a 1, |
x 0. |
||||||||||||||
x ln a |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
(ln x)' = |
1 |
|
, |
|
|
|
|
|
|
|
|
|
x 0. |
|
|
|
|
|
|
|||||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(ln | x | )' |
= |
1 |
|
, |
|
|
|
|
|
|
x 0. |
|
|
|
|
|||||||||||||||||||||
x |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
5. |
(sin x)' = cos x, |
|
|
|
|
|
x R. |
|
|
|
||||||||||||||||||||||||||
6. (cos x)' = −sin x, |
|
|
|
|
|
|
x R. |
|
|
|
||||||||||||||||||||||||||
7. (tgx)'= |
|
|
|
|
1 |
|
|
|
|
|
|
, |
|
|
|
|
|
x |
|
+ n , |
n Z. |
|||||||||||||||
cos2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||||||||
8. (ctgx)' = − |
|
|
|
|
|
|
|
1 |
|
|
|
|
, |
|
|
|
|
|
x n , |
|
n Z. |
|
||||||||||||||
|
sin2 |
x |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
9. (arcsinx)'= |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
, |
|
| x | 1 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − x 2 |
|
|
|
|
|
|
||||||||||||||
10. |
(arccosx)'= − |
|
|
|
|
|
1 |
|
|
|
|
|
, |
| x | 1 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
1 − x 2 |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
11. |
(arctgx)'= |
|
1 |
|
|
|
|
, |
|
|
|
|
x R. |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 + x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
12. |
(arcctgx)'= − |
|
|
1 |
|
|
|
|
|
, |
|
x R. |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + x 2 |
|
|
|
|
|
|
|||||||||||||
13. |
(shx)' = chx, |
x R. |
|
|
|
|
|
|
||||||||||||||||||||||||||||
14. |
(chx)' = shx, |
x R. |
|
|
|
|
|
|
||||||||||||||||||||||||||||
15. |
(thx)' = |
|
1 |
|
|
|
, |
|
|
|
|
|
x R. |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
ch2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
16. |
(cthx)'= − |
|
|
|
|
|
1 |
|
|
|
, |
|
|
|
x 0. |
|
|
|
||||||||||||||||||
|
sh2 x |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
88
6.3. Funkciyanıń differenciallanıwshılıǵı.
|
|
Funkciyanıń differencialı |
|
|
|||||
Meyli f (x) |
funkciya (a, b) da berilgen |
bolıp, x0 (a, b) , x0 + x (a, b) |
|||||||
bolsın. f (x0 ) = f (x0 + x) − f (x0 ) |
ayırma f (x) funkciyanıń x0 |
tochkadaǵı |
|||||||
ósimi delinedi. |
|
|
|
|
|
|
|
|
|
1-anıqlama. Eger f (x0 ) nı |
|
|
|
|
|
||||
|
|
f (x0 ) = A x + x |
|
|
|||||
kóriniste anıqlaw |
múmkin |
bolsa, |
onda |
f (x) funkciya x0 |
tochkada |
||||
differenciallanıwshı delinedi, bunda A = const, x → 0 , da → 0. |
|
||||||||
Teorema. f (x) funkciya |
x (a, b) tochkada differenciallanıwshı bolıwı |
||||||||
ushın onıń usı tochkada shekli |
f (x) tuwındıǵa iye bolıwı zárúrli hám jetkilikli. |
||||||||
◄Zárúrligi. |
f (x) funkciya |
x (a, b) |
tochkada |
differenciallanıwshı |
|||||
bolsın. Anıqlamaǵa tiykarlanıp, |
|
|
|
|
|
|
|
||
|
|
|
f (x) = A x + x |
|
|
||||
boladı, bunda A = const , x → 0 , da → 0. |
|
|
|
|
|||||
Bul teńlikten paydalanıp, f (x) |
= A + , |
|
|
|
|
||||
|
|
|
x |
|
|
|
|
|
|
|
lim |
f (x) = lim ( A + ) = A. |
|
|
|||||
|
x→0 |
|
x |
x→0 |
|
|
|
|
|
Demek, f (x) bar bolıp hám |
f (x) = A. |
|
|
|
|
||||
Jetkilikligi. f (x) funkciya x (a, b) da shekli f (x) |
tuwındıǵa iye bolsın. |
||||||||
Anıqlamaǵa muwapıq |
|
|
|
|
|
|
|
|
|
|
f (x) = lim |
f (x + x) − f (x) |
= lim f (x) |
|
|||||
|
|
|
|||||||
|
|
x→0 |
x |
|
x→0 |
x |
|
||
boladı. Eger f (x) |
− f (x) = bolsa, onnan |
|
|
|
|
||||
x |
|
|
|
|
|
|
|
|
|
f (x) = f (x) x + x
89
