
Matematikaliq analiz oqiw qollanba
.pdf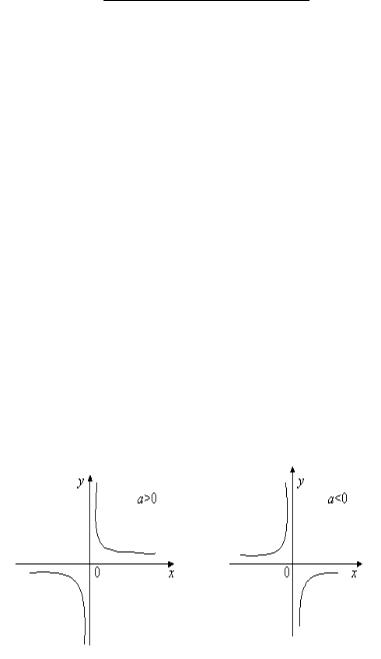
2. Bólshek racional funkciyalar. Bul
y= a0 + a1 x + a2 x 2 + ... + an x n b0 + b1 x + b2 x 2 + ... + bm x m
kórinistegi funkciya bólshek racional funkciya |
delinedi. Bunda a0 , a1 ,..., an |
hám b0 , b1 , ...,bm ler turaqlı sanlar n N , m N . |
Bul funkciya |
X = (− , + ) \ {x|b0 + b1x +... + bm xm = 0}
kóplikte anıqlanǵan.
Bólshek racional funkciyanıń bazı bir jaǵdayları: a) Keri proporcional baylanıs. Ol
y = |
a |
(х 0 а = const) |
|
х |
|||
|
|
||
kóriniske iye. Bul funkciya |
|
||
X = (− ,0) (0,+ ) = R \ {0}
kóplikte anıqlanǵan, taq funkciya, a nıń belgisine qarap funkciya (− , 0) hám
(0, + ) aralıqlardıń hár birinde kemeyiwshi yamasa ósiwshi boladı (4-sızılma).
4-sızılma |
|
|||
b) Bólshek sızıqlı funkciya. Ol tómendegi |
|
|||
y = |
aх + b |
|
||
cх + d |
|
|||
|
|
|
||
kóriniske iye boladı. Bul funkciya |
|
|
|
|
|
d |
|
||
X = R \ − |
|
|
|
(c 0) |
|
|
|||
|
|
c |
|
|
kóplikte anıqlanǵan.
50
Bizge belgili,
|
|
|
|
y = |
aх + b |
= |
bc − ad |
|
1 |
|
|
+ |
a |
. |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
cх + d |
|
|
c 2 |
|
х + |
d |
|
|
|
c |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
||
Demek, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
y = |
|
|
+ , |
|
= |
bc − ad |
|
, = |
d |
, |
= |
a |
. |
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
х + |
|
|
|
|
|
|
|
|
|
|
c |
|
c |
||||||||
Onıń grafigin y = |
a |
funkciya grafigi járdeminde sızıw múmkin. |
||||||||||||||||||||||
x |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3. Dárejeli funkciya. Bul |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
y = xa , (x 0) |
|
|
|
|
|
|
|
|
|
||||||||
kórinistegi funkciya dárejeli funkciya delinedi.
Bul funkciyanıń anıqlanıw kópligi a ǵa baylanıslı. Dárejeli funkciya a 0 ,
bolǵanda (0, + ) de ósiwshi, a 0 bolǵanda kemeyiwshi boladı. |
у = ха |
|
funkciya grafigi tegisliktiń (0,0 ) hám (1,1) noqatlarınan ótedi. |
|
|
4. Kórsetkishli funkciya. Bul |
|
|
у = а х |
|
|
kórinistegi funkciya kórsetkishli funkciya delinedi. Bunda a R , |
a 0 , |
a 1. |
Kórsetkishli funkciya (−, + ) anıqlanǵan, х R de a x 0 ; a 1 bolǵanda ósiwshi; 0 a 1 bolǵanda kemeyiwshi boladı.
Dara jaǵdayda, a = e bolsa, onda matematikada áhmiyetli rol tutatuǵın
у = е х funkciya payda boladı.
Kórsetkishli funkciyanıń grafigi Ox kósherinen joqarıda jaylasqan hám tegisliktiń (0,1) noqatsınan ótedi.
5. Logarifmlik funkciya. Bul
у = logа x
kórinistegi funkciya logarifmlik funkciya delinedi, bunda a 0 , a 1. Logarifmlik funkciya (0, + ) de anıqlanǵan, у = а х funkciyasına
salıstırǵanda keri; a 1 bolǵanda ósiwshi, 0 a 1 bolǵanda kemeyiwshi boladı.
51
Logarifmlik funkciyanıń grafigi Oy kósheriniń oń tárepinde jaylasqan hám tegisliktiń (0,1) noqatsınan ótedi.
6. Trigonometriyalıq funkciyalar. Bul
|
у = sin x, |
y = cos x, |
|
y = tgx, |
y = ctgx, |
|
||||||||||||||||
|
|
|
|
|
y = sec x, |
|
y = cos ecx |
|
|
|
|
|
||||||||||
funkciyalar trigonometriyalıq funkciyalar delinedi |
|
|
|
|
|
|
|
|
|
|||||||||||||
у = sin x, y = cos x funkciyalar |
R = (− , + ) de anıqlanǵan, |
2 periodlı |
||||||||||||||||||||
funkciyalar х R de |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 sin x 1, |
−1 cos x 1 |
|
|
|
|
|
||||||||||||||
boladı. y = tgx funkciya |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
k = |
|
|
|
|
|
|
|
||
X = R \ x R | x = (2k +1) |
2 |
0, 1, 2, ... |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
kóplikte anıqlanǵan periodlı funkciya, |
|
ctgx, |
secx, cosecx |
funkciyalar |
||||||||||||||||||
sin x, cosx, tgx lar arqalı tómendegishe ańlatıladı: |
|
|
|
|
|
|
|
|||||||||||||||
ctgx = |
1 |
, |
sec x = |
|
|
1 |
|
, |
|
cos ecx = |
|
1 |
. |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
tgx |
|
|
|
cos x |
|
|
|
|
|
|
sin x |
|
||||||||
7. Giperbolikalıq funkciyalar. Kórsetkishli у = eх |
funkciya járdeminde |
|||||||||||||||||||||
dúzilgen bul |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
еx − е−x |
еx + е−x |
|
еx − е−x |
|
еx + е−x |
|
|||||||||||||||
|
|
|
, |
|
|
, |
|
|
, |
|
|
|
|
|||||||||
2 |
|
2 |
|
еx + е−x |
|
еx − е−x |
|
|||||||||||||||
funkciyalar giperbolikalıq (sáykes túrde giperbolikalıq sinus, giperbolikalıq kosinus, giperbolikalıq tangens, giperbolikalıq kotangens) funkciyalar delinedi hám olar tómendegishe
|
еx − е−x |
|
еx + е−x |
|
|
еx − е−x |
|
еx + е−x |
||
shx = |
|
, chx = |
|
|
, thx = |
|
, |
cthx = |
|
|
2 |
2 |
|
еx + е−x |
еx − е−x |
||||||
belgilenedi. |
|
|
|
|
|
|
|
|
|
|
8. Keri trigonometriyalık funkciyalar. Meyli y = sin x funkciya R de |
||||||||||
anıqlanǵan hám onıń mánisleriniń kópligi |
|
|
|
|
|
|
|
|||
|
|
|
Y f |
= [−1, 1] |
|
|
|
|
|
|
52
boladı. Eger |
|
|
, |
|
bolsa, onda |
|
|
, |
|
hám Y f = [−1, 1] |
x − |
|
|
X = − |
|
|
|||||
|
|
2 |
|
2 |
|
|
2 |
|
2 |
|
kópliklerdiń elementleri óz-ara bir mánisli sáykeslikte boladı. y = sin x funkciyaǵa keri funkciya
у = аrc sin x
kóriniste belgilenedi. |
|
|
Usıǵan uqsas y = cos x, y = tgx, |
y = ctgx funkciyalarǵa salıstırǵanda keri |
|
funkciyalar sáykes túrde |
|
|
y = arccos x, y = arctgx, |
y = arcctgx , |
|
kóriniste belgilenedi. |
|
|
Bul у = аrc sin x , у = аrccos x , |
у = аrctgx , |
у = аrcctgx funkciyalar keri |
trigonometriyalıq funkciyalar delinedi. |
|
|
53
4-§. FUNKCIYANIŃ LIMITI
4.1. Funkciya limitiniń anıqlamaları
Meyli f (x) funkciya |
X R kóplikte |
berilgen bolıp, x0 noqatta X |
|||||||||||||||||||||||
kópliktiń limit noqatı bolsın. x0 |
noqatga umtılıwshı qálegen xn : |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
x1, x2 , ..., xn ,... |
|
(xn X , |
xn x0 ) |
|
|
|
|
|
|||||||||||
izbe-izlikti alıp, funkciya mánislerinen ibarat { f (xn )}: |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
f (x1 ), |
|
f (x2 ), ..., |
f (xn ), ... |
|
|
|
|
|
||||||||||
izbe-izlikti payda etemiz. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1-anıqlama. (Geyne). Eger |
|
|
|
n → de |
|
xn |
→ x0 |
(xn X , |
xn |
x0 ) |
|||||||||||||||
bolatuǵın qálegen |
{ xn } izbe-izlik ushın n → de |
f (xn ) →b bolsa, onda b ǵa |
|||||||||||||||||||||||
f (x) funkciyanıńg x0 |
noqatdaǵı limiti delinedi hám x → x0 |
de |
f (x) → b |
||||||||||||||||||||||
yaǵnıy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim f (x) = b |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
x→x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
kóriniste belgilenedi. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Eskertiw. |
Eger |
n → |
de |
|
xn → x0 |
(xn X , |
xn |
x0 ) |
hám |
||||||||||||||||
yn → x0 |
( yn X , |
|
yn x0 ) |
bolatuǵın |
túrli |
|
{xn }, {yn } |
izbe-izlikler |
ushın |
||||||||||||||||
n → de |
f (xn ) →b1 , f ( yn ) →b2 |
bolıp, |
b1 b2 |
bolsa, onda |
f (x) |
funkciya |
|||||||||||||||||||
x → x0 de limitke iye emes delinedi. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1-mısal. f (x) = |
|
x 2 |
−16 |
|
funkciyanıń |
x0 = 4 noqatdaǵı limitin tabıń. |
|
||||||||||||||||||
|
x 2 |
− 4x |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
◄ Meyli lim xn |
= 4, |
( xn 4, n = 1, 2, ...) |
izbe-izlikti alayıq. Onda |
|
|
|
|||||||||||||||||||
|
n→ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (xn ) = |
|
|
xn2 −16 |
= |
xn + 4 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
xn2 |
− 4xn |
|
xn |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
bolıp, n → da |
f (xn ) → 2 boladı. Demek, |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
lim |
|
|
x 2 |
−16 |
= 2. ► |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
n→ x 2 |
− |
4x |
|
|
|
|
|
|
|
|
|
|
|
||||
54
2-mısal. f (x) = sin |
1 |
|
|
funkciyanıń x → 0 degi limitke iye emesligi kórsetiń. |
||||||||||||||||||||||||||||
|
x |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
◄ n → de |
x' |
|
|
|
= |
|
|
|
|
2 |
|
|
|
|
|
→ 0, |
x' ' |
= |
|
|
2 |
|
→ 0 boladı. Bul izbe- |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
n |
|
|
|
|
|
|
(4n |
−1) |
|
|
|
n |
|
(4n |
+1) |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
izlikler ushın f (xn' ) = |
4n −1 |
= −1, |
|
|
|
f (xn'' ) = |
4n +1 |
=1 |
bolıp, n → de |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
f (xn' ) → −1, |
f (xn'' ) →1 |
|
|
||||||||||||||||
boladı. Demek, berilgen funkciya |
x0 |
|
|
= 0 noqatda limitke iye emes. ► |
|
|||||||||||||||||||||||||||
2-anıqlama. (Koshi). Eger |
|
|
0 san alınǵanda hám sonday = ( ) 0 |
|||||||||||||||||||||||||||||
tabılsa, x X (U (x0 ) \ {x0 }) ushın |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| f (x) − b | |
|
|
|
|
|||||||
teńsizlik orınlı bolsa, onda b sanı f (x) |
funkciyanıń x0 noqatdaǵı limiti delinedi: |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim f (x) = b . |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→x0 |
|
|
|
|
|
|
|
|
|||
3-mısal. f (x) = C = const |
|
|
|
(C R) bolsın. Bul funkciya ushın |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim f (x) = C |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→x0 |
|
|
|
|
|
|
|
|
|||
boladı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4-mısal. Bul |
f (x) = |
|
x 2 −1 |
funkciyanıń |
x0 =1 noqatdaǵı limiti 2 ge teń |
|||||||||||||||||||||||||||
|
|
x −1 |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ekenligii kórsetiń. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
◄ 0 sanına karap |
|
= |
dep alsaq, |
onda |
| x −1 | |
(x 1) |
||||||||||||||||||||||||||
teńsizlikti qanaatlandırıwshı qálegen |
|
x te |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
x |
2 −1 |
− 2 |
|
=| x +1 − 2 | =| x −1| = |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x −1 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
boladı. Demek, lim |
x 2 |
−1 |
= 2.► |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
x |
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
x→x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3-anıqlama. Eger 0 |
san alınǵanda hám sonday 0 san tabılsa, |
|||||||||||||||||||||||||||||||
x X (U (x0 ) \ {x0 }) |
|
|
|
ushın |
|
|
f (x) |
teńsizlik |
orınlı bolsa, onda |
f (x) |
||||||||||||||||||||||
funkciyanıń x0 noqatdaǵı limiti + dep ataladı hám |
|
|
|
|
||||||||||||||||||||||||||||
55
|
|
|
|
|
|
|
|
|
|
lim f (x) = + |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
x→x0 |
|
|
|
|
|
|
|
|||||||||
kóriniste belgilenedi. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Meyli f (x) funkciya |
X R kóplikte berilgen bolıp, x0 = + noqat X |
|||||||||||||||||||||||||
kópliktiń limit noqatı bolsın. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
4-anıqlama. Eger 0 |
san alınǵanda da sonday 0 tabılsa x X , |
|||||||||||||||||||||||||
x ushın |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
| f (x) − b | |
|
|
||||||||||||||
teńsizlik orınlı bolsa, onda b sanı f (x) |
funkciyanıń x0 = + degi limiti delinedi |
|||||||||||||||||||||||||
hám |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
lim f (x) = b |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
x→+ |
|
|
|
|
|
|
|
|||||||||
kórinisinde belgilenedi. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
5-mısal. Meyli X = (0, + ) , x0 |
=+ , |
|
f (x) = |
1 |
|
bolsın, onda |
||||||||||||||||||||
x |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
lim |
1 |
|
= 0 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
x→+ x |
|
|
|
|
|
|
|
|||||||||
boladı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
◄Haqıyqatında da 0 sanın alayıq. x 0 |
ushın |
|||||||||||||||||||||||||
|
|
|
|
− 0 |
|
= |
1 |
|
x |
1 |
. |
|||||||||||||||
|
|
|
|
1 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
x |
|
|
|
|
|
||||||||||
Demek, = |
1 |
bolsa, onda |
x ushın |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
1 |
− 0 |
|
= |
1 |
|
1 |
= |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
x |
|
|
|
||||||||||
boladı. ►
Funkciya limiti anıqlamalarınıń ekvivalentligi.
Teorema. Funkciya limitinıń Koshi hám Geyne anıqlamaları ekvivalent anıqlama boladı.
56
Funkciyanıń oń hám shep limitleri. Meyli |
f (x) funkciya X R kóplikte |
berilgen, x0 noqat X tıń shep limit noqatı bolıp, |
|
(x0 − , x0 ) X |
( 0) |
bolsın. |
|
5-anıqlama. Eger |
|
0, 0, x (x0 − , x0 ) : | f (x) −b |
bolsa, onda b san f (x) funkciyanıń x0 |
noqatdaǵı shep limiti delinedi hám |
||
b = |
lim |
f (x) = f (x0 − 0) |
|
|
x→x0 −0 |
|
|
kóriniste belgilenedi. |
|
|
|
Meyli f (x) funkciya X R kóplikte berilgen, x0 noqat X tıń oń limit |
|||
noqatı bolıp, |
|
|
|
(x0 , x0 + ) X |
( 0) |
||
bolsın. |
|
|
|
6-anıqlama. Eger |
|
|
|
0, 0, x (x0 , x0 + ) : | f (x) −b | |
|||
bolsa, onda b san f (x) funkciyanıń x0 |
noqatdaǵı oń limiti delinedi hám |
||
b = |
lim |
f (x) = f (x0 + 0) |
|
|
x→x0 +0 |
|
|
kóriniste belgilenedi. |
|
|
|
Máselen, |
|
|
|
|
1, eger x 0 |
bolsa, |
|
|
|
0, eger x = 0 |
bolsa, |
f (x) = |
|||
|
|
|
bolsa |
|
−1, eger x 0 |
||
funkciyanıń 0 noqatdaǵı oń limiti 1, shep limiti -1 boladı.
4.2. Limitke iye bolǵan funkciyalardıń qásiyetleri. Limittiń bar bolıwı
Shekli limitke iye bolǵan funkciyalar da jıynaqlı izbe-izlik sıyaqlı qásiyetlerge iye.
57

Meyli f (x) funkciya X R kóplikte berilgen bolıp, x0 R noqat X tıń
limit noqatı bolsın. |
|
|
|
1-qásiyet. Eger x → x0 da f (x) funkciya limitke iye bolsa, |
onda ol jalǵız |
||
boladı. |
|
|
|
2-qásiyet. Eger |
lim f (x) = b , (b − shekli san) bolsa, onda |
f (x) funkciya |
|
|
x→x0 |
|
|
shegaralanǵan boladı. |
|
|
|
3-qásiyet. Eger |
lim f (x) = b bolıp, b p bolsa, onda |
f (x) p boladı. |
|
|
x→x0 |
|
|
Meyli f (x) hám g (x) funkciyalar X R kóplikte berilgen bolıp, x0 R noqat X kópliktiń limit noqatı bolsın.
4-qásiyet. Eger lim f (x) = b1 , |
|
lim g(x) = b2 bolıp, x X |
de f (x) g(x) |
x→x0 |
x→x0 |
|
|
teńsizlik orınlı bolsa, onda b1 b2 , yaǵnıy |
|
||
lim f (x) lim g(x) |
|
||
x→x0 |
x→x0 |
|
|
boladı. |
|
|
|
5- qásiyet. Meyli |
|
|
|
lim f (x) = b1, |
|
lim g(x) = b2 , (b1, b2 R) |
|
x→x0 |
|
x→x0 |
|
limitler bar bolsın. Onda
a) |
c R |
da lim (c f (x)) = с lim f (x) ; |
|
|
|
x→x0 |
x→x0 |
b) |
lim ( f (x) + g(x)) = lim f (x) + lim g(x); |
||
|
x→x0 |
x→x0 |
x→x0 |
v) |
lim ( f (x) g(x)) = lim |
f (x) lim g(x); |
|
|
x→x0 |
x→x0 |
x→x0 |
g) Eger b2 |
0 bolsa, onda lim |
|
x→x0 |
f (x)
g(x)
lim f (x)
= x→x0
lim g(x)
x→x0
boladı.
1-mısal. lim |
x + x 2 |
+ x3 + ... + x n − n |
limitti esaplań. |
|
x −1 |
||
x→1 |
|
|
◄ Bul limitti joqarıdaǵı qásiyetlerden paydalanıp esaplaymız:
58

lim |
x + x2 |
+ x3 +...+ xn −n |
= lim |
(x −1) +(x2 −1) +(x3 −1) +...+(xn −1) |
= |
|
x −1 |
x −1 |
|||
x→ 1 |
|
x→ 1 |
|
|
(x −1)[1 + (x +1)+ (x2 |
|
|
|
+ x +1)+ ... + (xn−1 + xn−2 + x +1)] |
||||||||||||||||||||||||||||||||||
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
x→1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
=1 + 2 + 3 + ... + n = |
n(n +1) |
|
.► |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2-mısal. lim |
1 − cos x |
limitt esaplań. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
x→0 |
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
◄ Bizge belgili, 1 − cos x = |
2sin |
2 |
|
x |
. Sonı esapqa alıp tabamız: |
||||||||||||||||||||||||||||||||||
|
|
2 |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 x |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
2 |
|
|||||
|
|
1 − cos x |
|
|
|
|
2 sin |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
sin |
|
|
|
|
|||||||||||||
|
lim |
= lim |
2 |
|
= lim |
|
2 |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
||||||||||||||||||
|
|
x 2 |
|
|
|
|
|
|
|
|
x 2 |
2 |
|
|
x |
|
|
||||||||||||||||||||||
|
x→0 |
|
|
|
x→0 |
|
|
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||
|
|
|
|
|
|
|
sin |
x |
|
|
|
|
|
sin |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
1 |
|
. ► |
|
|
|
||||||||||||||||
|
|
= |
|
lim |
|
|
|
|
|
|
|
lim |
|
|
|
|
|
= |
|
|
|
|
|
|
|||||||||||||||
|
|
2 |
|
|
x |
|
|
|
|
x |
|
|
2 |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
x→0 |
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Funkciya limitiniń bar bolıwı. Meyli |
|
f (x) |
funkciya |
X R kóplikte |
|||||||||||||||||||||||||||||||||||
berilgen bolıp, ( x0 − , |
x0 ) X bolsın |
|
( 0 ). , |
|
x0 R noqat X kópliktiń |
||||||||||||||||||||||||||||||||||
limit noqatı boladı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1-teorema. Eger |
f (x) funkciya |
|
|
|
X kóplikte |
ósiwshi bolıp, ol joqarıdan |
|||||||||||||||||||||||||||||||||
shegaralanǵan bolsa, onda funkciya x0 |
|
noqatda |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
lim f (x)
x→x0 −0
limitke iye boladı.
◄ Meyli f (x) funkciyanıń mánislerinen ibarat bolǵan bul
F = f (x) x X x x0
kóplikti qaraymız. Teoremanıń shártin boyınsha bul kóplik joqarıdan shegaralanǵan boladı. Onda kópliktiń anıq shegarasınıń bar bolıwı haqqındaǵı
59
