
Matematikaliq analiz oqiw qollanba
.pdf| xn − xm | |
1 |
+ |
1 |
|
|
|
|||
|
n0 |
n0 |
||
boladı. ►
Teorema. (Koshi teoreması). Izbe-izliktiń jıynaqlı bolıwı ushın onıń
fundamental bolıwı zárúrli hám jetkilikli. |
|
|
|
|||||
◄Zárúrligi. |
{xn } |
izbe-izlik jıynaqlı bolıp, lim xn = а bolsın. Limit |
||||||
|
|
|
|
|
|
n→ |
|
|
anıqlamasına tiykarlanıp |
|
|
|
|
|
|
|
|
|
0, |
n0 N, |
n n0 : | xn − a | |
. |
|
|||
|
|
|
|
|
|
|
2 |
|
Solay etip, |
m n |
0 |
: | x |
m |
− a | |
boladı. Nátijede |
n n , |
m n |
|
|
|
2 |
|
0 |
0 |
||
|
|
|
|
|
|
|
|
|
uchun
| xn − xm |=| xn − a + a − xm | | xn − a | + | xm − a | kelip shıǵadı. Demek, {xn } fundamental izbe-izlik.
Jetkilikligi. Meyli {xn } fundamental izbe-izlik bolsın:
0, n0 N, n n0 , m n0 : | xn − xm | .
Eger m n0 shártti qanaatlandırıwshı m fikserlengen bolsa, onda
| xn − xm | xm − xn xm +
bolıp
{xnk }
{xn } izbe-izliktiń shegaralanǵanlıǵı kelip shıǵadı.
Bol’cano-Veyershrass teoremasına tiykarlanıp bul izbe-izlikten jıynaqlı úles
izbe-izlikti ajratıw múmkin lim xn = а.
n→ k
Demek,
0, k0 N, k k0 : | xn k − a |
boladı. Eger m = nk bolsa, onda
| xn − xnk |
boladı. Keyingi eki teńsizliklerden
| xn − a |=| xn − xnk + xnk − a | | xn − xnk | + | xnk − a | 2
kelip shıǵadı. Demek, lim xn = а. ►
n→
40
3-§. FUNKCIYA
3.1. Funkciya túsinigi
Meyli E kópligin F kóplikke sáwlelendiriw f : E →F
berilgen bolıp, E = F , F = R dep belgileymiz. Onda hár bir haqıyqıy x sanǵa bazı bir haqıyqıy sandı sáykes qoyıwshı
|
f |
|
f : F →R ( x → y ) |
|
|
sáwlelendiriwine kelemiz. Bunnan funkciya túsinigine alıp keledi. |
|
|
Meyli X R , Y R kóplikler berilgen bolıp, x hám y |
ózgeriwshiler |
|
sáykes tárizde usı kópliklerde ózgersin: x X , |
y Y . |
|
1-anıqlama. Eger X kópliktegi hár bir |
x sanǵa bazı bir |
f qaǵıydaǵa |
qarata Y ge tek bir y san sáykes qoyılǵan bolsa, onda X kóplikte funkciya berilgen (anıqlanǵan) delinedi hám
f : x → y yaǵnıy y = f (x)
kórinisinde belgilenedi. Bunda X - funkciyanıń anıqlanıw oblastı, Y - funkciyanıń mánisler kópligi (oblastı) delinedi. x - ǵárezli ózgeriwshi yamasa funkciyanıń argumenti.
Mısallar. 1. X = (− ,+ ) , Y = (0,+ ) bolıp, f qaǵıyda f : x → y = x2 +1
bolsın. Bul jaǵdayda hár bir x X ge bir x2 +1 Y sáykes qoyılıp, y = x2 +1
funkciyaǵa iye bolamız.
2. Hár bir racional sanǵa 1 di, hár bir irracional sanǵa 0 di sáykes qoyıw nátiyjesinde funkciya payda boladı. Ádette bul Dirixle funkciyası bolıp D(x) kóriniste belgilenedi:
41
|
|
D (x) = |
|
|
|
|
|
|
1 , eger |
x |
racional san, |
|
|
|
0 , eger |
x |
irracional san |
Solay etip, |
y = f (x) funkciya |
ol X kóplik, Y kóplik hám hár bir x X bir |
|||
y Y tı sáykes qoyıwshı f |
qaǵıydanıń beriliwi menen anıqlanadı. |
||||
Meyli |
y = f (x) funkciya |
X R kóplikte berilgen bolsın. x0 X noqatǵa |
|||
sáykes keliwshi y0 noqat |
y = f (x) funkciyanıń x = x0 noqatdaǵı mánisi delinedi |
||||
hám f (x0 )= y0 kóriniste belgilenedi.
Tegislikte dekart koordinatalar sistemasın alamız. Tegisliktegi ( x, f (x))
noqatlardan ibarat
( x , f (x)) = ( x , f (x)) x X , f (x) Y
kóplik y = f (x) funkciyanıń grafigi delinedi. Máselen,
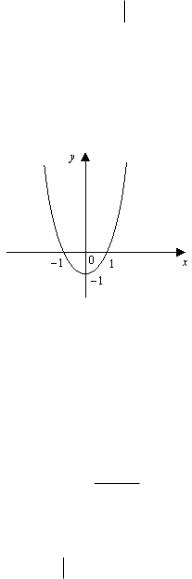
y = x2 −1 ( x X = − 2, 2 )
funkciyanıń grafigi 1-sızılmada suwretlengen.
1-sızılma.
Funkciya anıqlamasındaǵı f qaǵıyda hár túrli bolıwı múmkin.
a) Kóbinese x hám y ózgeriwshiler arasındaǵı baylanıs formulalar járdeminde belgilenedi. Bul funkciyanıń analitikalıq usılda beriliwshi delinedi.
Máselen,
y = 
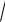 1 − x2
1 − x2
funkciya analitik usılda berilgen bolıp onın anıqlanıw kópligi
X = x R −1 x 1 = −1,1
boladı.
42
Meyli x hám y ózgeriwshiler arasındaǵı baylanıs tómendegi formulalar járdeminde berilgen bolsın:
1, eger x 0, y = f (x) =
−1, eger x 0.
Bul funkciyanıń anıqlanıw kópligi X = R \ 0 bolıp, mánisleri kópligine iye Y = −1,1 boladı. Ádette bul funkciya y = sign x kórinistegi belgilenedi.
b) Ayırım jaǵdaylarda x X , y Y ózgeriwshiler arasındaǵı baylanıs
tablicalar arqalı bolıwı múmkin. Máselen, kún dawamında hawa temperaturasın
baqlaǵanımızda t1 waqıtta hawa temperaturası T1 , t2 |
waqıtta hawa temperaturası |
|||||||
T2 h.t.b. bolsın. Nátiyjede tómendegi tablica payda boladı. |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
t – waqıt |
t1 |
t2 |
t3 |
|
... |
tn |
|
|
|
|
|
|
|
|
|
|
|
T – |
T1 |
T2 |
T3 |
|
... |
Tn |
|
|
temperatura |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Bul tablica t waqıt penen hawa temperaturası T arasındaǵı baylanıstı ańlatadı, bunda t -argument, T bolsa t nıń funkciyası boladı.
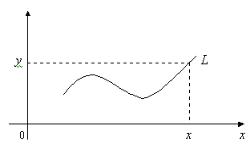
v) x hám y ózgeriwshiler arasındaǵı baylanıs tegislikte bazı bir iymek sızıq arqalı hám ańlatıw múmkin (2-sızılma).
2- sızılma.
Máselen, 2- sızılmada suwretlengen L iymek sızıq berilgen bolsın. segmenttegi hár bir noqatdan ótkizilgen perpendikulyar L sızıqtı tek bir noqatda kesilsin. x a,b noqatdan perpendikulyar shıǵarıp, onıń L sızıq penen kesilisiw noqatın tabamız. Alınǵan x noqatǵa kesilisiw noqatınıń ordinatası y ti sáykes qoyamız. Nátiyjede hár bir x a,b ǵa bir y sáykes qoyılıp, funkciya
43
payda boladı. Bunda x penen y arasındaǵı baylanıstı berilgen L iymek sızıq orınlaydı.
Meyli f1(x) funkciya X1 R kóplikte, f2 (x) funkciya bolsa X 2 R kóplikte anıqlanǵan bolsın.
Eger
1)X1 = X 2
2)x X1 da f1(x)= f2 (x)
bolsa, onda f1(x) hámde f2 (x) funkciyalar óz-ara teń delinedi hám f1(x)= f2 (x) kóriniste belgilenedi.
Funkciyanıń shegaralanǵanlıǵı. f (x) funkciya X R kóplikte berilgen bolsın.
2-anıqlama. Eger sonday turaqlı M sanın tabılsa, x X ushın f (x) M teńsizlik orınlı bolsa, onda f (x) funkciya X kóplikte joqarıdan shegaralanǵan delinedi. Eger sonday turaqlı m sanı tabılsa, x X ushın f (x) m teńsizlik orınlı bolsa, onda f (x) funkciya X kóplikte tómennen shegaralanǵan delinedi.
3-anıqlama. Eger f (x) funkciya X kóplikte hám joqarıdan, hám tómennen shegaralanǵan bolsa, onda f (x) funkciya X kóplikte shegaralanǵan delinedi.
1-mısal. Usı |
f (x) = |
1 + x 2 |
|
funkciyanı |
qarayıq. Bul |
funkciya R de |
||||||||||||||||
1 + x 4 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
shegaralanǵan boladı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
◄ Solay etip, x R de f (x) = |
1 + x 2 |
0. |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1 |
+ x 4 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Demek, berilgen funkciya R de tómennen shegaralanǵan. |
|
|
|
|
|
|||||||||||||||||
Sonıń menen birge, f (x) funkciya ushın |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
f (x) = |
|
|
1 |
|
|
|
+ |
|
x 2 |
1 + |
|
x 2 |
|
|
|
|
|
|
|||
|
|
+ x 4 |
|
+ x 4 |
|
+ x 4 |
|
|
|
|
|
|||||||||||
|
|
1 |
1 |
1 |
|
|
|
|
|
|||||||||||||
boladı. Endi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 (x2 −1)2 = x4 − 2x2 +1 |
|
2x2 x4 +1 |
x2 |
|
|
1 |
|
|||||||||||||||
|
x4 +1 |
2 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
44
itibarǵa alsaq, onda |
f (x) 1 + |
1 |
= |
3 |
. |
Bul |
f (x) funkciyanıń joqarıdan |
|
2 |
2 |
|||||||
|
|
|
|
|
|
shegaralanǵanlıǵın bildiredi. Demek, berilgen funkciya R de shegaralanǵan. ► 4-anıqlama. Eger hár qanday M 0 san alınǵanda hám sonday x0 X
noqatı tabılsa,
f (x0 ) M
teńsizlik orınlı bolsa, onda f (x) funkciya X kóplikte joqarıdan shegaralanbaǵan delinedi.
Periodlı funkciyalar. Jup hám taq funkciyalar. f (x) funkciya X R kóplikte berilgen bolsın.
5-anıqlama. Eger sonday turaqlı T (T 0 ) san bar bolsa, onda x X
ushın
1)x − T X , x + T X
2)f ( x + T )= f (x)
bolsa, onda f (x) periodlı funkciya delinedi, T san bolsa f (x) funkciyanıń periodı delinedi.
Máselen, f (x)= sin x , f (x)= cos x funkciyalar periodlı funkciyalar bolıp, olardıń periodı 2 ga, f (x)= tgx , f (x)= ctgx funkciyalardıń periodı bolsa ǵa
teń. Periodlı funkciyalar tómendegi qásiyetlerge iye: |
|
|
|
a) Eger |
f (x) periodlı funkciya bolıp, onıń periodı T (T 0 ) bolsa, onda |
||
|
Tn = nT (n = 1, 2, ) |
|
|
sanlar hám usı funkciyanıń periodı boladı. |
|
|
|
b) Eger T1 hám T2 sanlar f (x) funkciyanıń periodı bolsa, onda T1 + T2 0 |
|||
hámde T1 −T2 |
(T1 T2 ) sanlar hám f (x) funkciyanıń periodı boladı. |
||
v) Eger |
f (x) hámde g(x) funkciyalar periodlı funkciyalar bolıp, olardıń |
||
hár biriniń periodı T (T 0) bolsa, onda |
|
|
|
|
f (x)+ g(x), f (x)− g(x), f (x) g(x), |
f (x) |
(g(x) 0 ) |
|
g(x) |
||
|
|
|
|
45
funkciyalar hám periodlı funkciyalar bolıp, T san olardıń hám periodı boladı.
Bizge belgili, x X ( X R ) ushın − x X bolsa, |
onda X kóplik O |
noqatǵa salıstırǵanda simmetriyalı kóplik delinedi. |
|
Meyli O noqatǵa salıstırǵanda simmetriyalı bolǵan |
X kóplikte f (x) |
funkciya berilgen bolsın.
6-anıqlama. Eger x X ushın f (− x)= f (x) teńlik orınlı bolsa, onda f (x) jup funkciya delinedi. Eger x X ushın f (− x)= − f (x) teńlik orınlı bolsa, onda f (x) taq funkciya delinedi.
Máselen, f (x)= x2 +1 jup funkciya, f (x)= x3 + x bolsa taq funkciya boladı. Bul f (x)= x2 − x funkciya jup ta emes, taq ta emes.
Eger |
f (x) hám g(x) jup funkciyalar bolsa, onda |
|||||||
f (x)+ g(x), f (x)− g(x), |
f (x) g(x), |
f (x) |
|
(g(x) 0 ) |
||||
g(x) |
||||||||
|
|
|
|
|
|
|||
funkciyalar da jup boladı. |
|
|
|
|
|
|
||
Eger |
f (x) hám g(x) taq funkciyalar bolsa, onda |
|
||||||
|
f (x)+ g(x), f (x)− g(x) |
|||||||
funkciyalar taq boladı, |
|
|
|
|
|
|
||
|
f (x) g(x), |
f (x) |
|
(g(x) 0 ) |
||||
|
g(x) |
|||||||
|
|
|
|
|
|
|||
funkciyalar bolsa jup boladı. |
|
|
|
|
|
|
||
Jup |
funkciyanıń grafigi |
ordinatalar |
kósherine salıstırǵanda, taq |
|||||
funkciyanıń grafigi koordinatalar basına salıstırǵanda simmetrik jaylasqan boladı. Monoton funkciyalar. Meyli f (x) funkciya X R kóplikte berilgen bolsın.
7-anıqlama. |
Eger x1 , x2 X |
ushın x1 x2 bolǵanda |
f (x1 ) f (x2 ) |
|
teńsizlik orınlı bolsa, onda |
f (x) funkciya X kóplikte ósiwshi delinedi. Eger |
|||
x1 , x2 X ushın |
x1 x2 |
bolǵanda |
f (x1 ) f (x2 ) teńsizlik orınlı bolsa, onda |
|
f (x) funkciya X kóplikte qatań ósiwshi delinedi.
46
8-anıqlama. Eger x1 , x2 X ushın x1 x2 bolǵanda f (x1 ) f (x2 ) teńsizlik orınlı bolsa, onda f (x) funkciya X kóplikte kemeyiwshi delinedi. Eger
x1 , x2 X ushın |
x1 x2 bolǵanda |
f (x1 ) f (x2 ) |
teńsizlik orınlı bolsa, onda |
|||||||||||||||||||
f (x) funkciya X kóplikte qatań kemeyiwshi delinedi. |
|
|
|
|
|
|
|
|||||||||||||||
Ósiwshi hám kemeyiwshi funkciyalar ulıwma monoton funkciyalar delinedi. |
||||||||||||||||||||||
2-mısal. Bul |
f (x) = |
|
x |
funkciyanıń X = 1,+ ) kóplikte kemeyiwshi |
||||||||||||||||||
|
|
|
||||||||||||||||||||
1 + x 2 |
||||||||||||||||||||||
ekenligin dálilleń. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
◄ 1, + ) da x1 hám x2 |
noqatların alıp, x1 x2 |
bolsın desek. Onda |
||||||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
x |
2 |
|
|
|
x + x x 2 |
− x |
2 |
− x |
x 2 |
|||
f (x ) − f (x |
|
) = |
|
|
1 |
− |
|
|
|
= |
|
1 |
1 2 |
|
|
2 1 |
= |
|||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1 |
|
|
1 + x 2 |
1 + x 2 |
|
|
(1 + x 2 )(1 + x 2 ) |
|||||||||||||||
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
1 |
|
2 |
|
|
|
|
= |
x1 − x2 + x1 x2 (x2 − x1 ) |
|
= |
(x1 − x2 )(1 − x1 x2 ) |
|
|||||||||||||||||
|
|
|||||||||||||||||||||
|
|
(1 + x2 )(1 + x2 ) |
|
|
|
|
|
(1 + x2 )(1 + x2 ) |
|
|
|
|||||||||||
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
boladı. Keyingi teńlikte x1 − x2 0, 1 − x1 |
x2 0 esapqa alıp, |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
f (x1 )− f (x2 ) 0 |
|
|
|
|
|
|
|
||||||||
yaǵnıy, f (x1 ) f (x2 ) ekenin tabamız. Demek, |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
x1 x2 |
f (x1 ) f (x2 ).► |
|
|
|
|
|
||||||||||||
Meyli f (x) hám g(x) funkciyalar X R kóplikte ósiwshi (kemeyiwshi)
bolıp, C = const bolsın. Bul jaǵdayda
a)f (x)+ C funkciya ósiwshi (kemeyiwshi)boladı.
b)C 0 bolǵanda C f (x) ósiwshi, C 0 bolǵanda C f (x) kemeyiwshi
boladı.
v) f (x)+ g(x) funkciya ósiwshi (kemeyiwshi) boladı.
Keri funkciya. Quramalı funkciyalar. y = f (x) funkciya X R kóplikte berilgen bolıp, bul funkciyanıń mánislerinen ibarat kóplik
Y f ={ f (x) | x X }
bolsın.
47
Meyli bazı bir qaǵıydasına karap Y f , kóplikten alınǵan hár bir y ke X kópliktegi bir x sáykes qoyılǵan bolsın. Bunday sáykeslik nátiyjesinde funkciya payda boladı. Ádette, bul funkciya y = f (x) ge salıstırǵanda keri funkciya delinedi
hám x = f −1( y) |
kóriniste belgilenedi. |
|
|
|
|
|
|
||||
Máselen, |
y = |
1 |
x +1 |
funkciyaǵa |
salıstırǵanda |
keri |
funkciya |
||||
|
|||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
x = 2 y −1 boladı. |
|
|
|
|
|
|
|
||||
Joqarıda aytılǵanlardan y = f (x) de x argument, y |
bolsa x tıń funkciyası, |
||||||||||
keri x = f |
−1( y) |
funkciyada y |
argument, |
x |
bolsa |
y |
tıń |
funkciyasi bolıwı |
|||
kórinedi. |
|
|
|
|
|
|
|
|
|
|
|
Qolaylıq |
ushın keri funkciya argumenti |
x , onıń funkciyası |
y penen |
||||||||
belgilenedi: |
y = g(x). |
|
|
|
|
|
|
|
|||
y = f (x) funkciyaǵa keri |
g(x) funkciya grafigi |
f (x) |
funkciya grafigin I |
||||||||
hám III sherekler bissektrisası átirapında 1800 ǵa aylandırıw nátiyjesinde p ayda boladı.
Meyli Y f kóplikte u = F(y) funkciya berilgen bolsın. Nátiyjede X kóplikten alınǵan hár bir x ge Y f kóplikte bir y :
f : x → y ( y = f (x)), hám Y f kópliktegi bunday y sanǵa bir u :
F : y → u (u = F ( y))
san sáykes qoyıladı. Demek, X kóplikten alınǵan hár bir x sanǵa bir u san sáykes qoyılıp, jańa funkciya payda boladı: u = F( f (x)). Ádette bunday funkciyalar quramalı funkciya delinedi.
3.2. Elementar funkciyalar hám onıń qásiyetleri
Bul paragrafta elementar funkciyalar haqqında tiykarǵı maǵlıwmatlardı keltiremiz.
48
1. Pútin racional funkciyalar.
Bul
y = a0 + a1x + a2 x2 + ... + an−1xn−1 + an xn
kórinistegi funkciya pútin racional funkciya delinedi. Bunda a0 , a1,..., an – turaqlı sanlar, n N . Bul funkciya R = (−, + ) de anıqlanǵan.
Pútin racional funkciyanıń bazı dara jaǵdayları: a) Sızıqlı funkciya. Bul funkciya
|
|
y = aх + b |
|
|
|
(a 0) |
|
||
kóriniske iye, bunda a , b turaqlı sanlar. |
|
|
|
|
|
|
|
||
Sızıqlı funkciya (−, + ) de anıqlanǵan a 0 bolǵanda ósiwshi, a 0 |
|||||||||
bolǵanda kemeyiwshi grafigi tegisliktegi |
tuwrı sızıqtan ibarat. |
|
|||||||
b) Kvadrat funkciya. Bul funkciya |
|
|
|
|
|
|
|
||
|
y = aх2 + bx + c |
|
|
(a 0) |
|
||||
kórinisine iye, bunda a , b , c – turaqlı sanlar. |
|
|
|
|
|
|
|||
Kvadrat funkciya R de anıqlanǵan bolıp, onıń grafigi p arabolanı ańlatadı. |
|||||||||
Bunnan |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
b 2 |
|
b2 − 4ac |
|
|
y = aх |
|
+ bx + c = а x + |
|
|
|
− |
|
. |
|
|
|
|
|
||||||
|
|
|
|
|
2a |
|
4a |
|
|
Parabolanıń tegislikte jaylasıwı a hám |
D = b2 − 4ac lerdiń belgisine baylanıslı |
||||||||
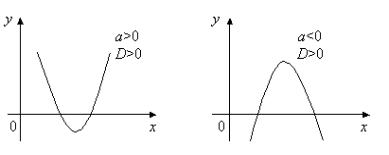
boladı. Máselen, a 0, D 0 hám a 0 , |
D 0 |
bolǵanda |
onıń grafigi 3- |
||||||
sızılmada súwretlengen parabolalar kórinisinde boladı. |
|
|
|||||||
3-sızılma.
49
