Добавил:

aysultan Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Каракалпакский государственный университет им. Бердаха

Предмет:

Дискретная математика

Файл:

Matematikaliq analiz oqiw qollanba

.pdf

Скачиваний:

Добавлен:

10.08.2024

Размер:

7.89 Mб

Скачать

☆

<<< < Предыдущая 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 3435 / 3635 36 > Следующая >>>

18.4. Birinshi túr betlik integralı

Birinshi túr betlik integralı túsinigi. Keńislikte

		z = z(x, y)		(1)
teńleme menen anıqlanǵan S betlikti qaraymız. Bunda				z(x, y) funkciya
D R2	kóplikte úzliksiz hám úzliksiz zx (x, y), z y (x, y)		dara tuwındılarǵa
iye. Meyli (1) betlik maydanǵa iye bolıp, onıń maydanı

	S = 1 + z x2 (x, y) + z y2 (x, y)dxdy
	D
boladı.
Meyli S	betlikte f (x, y, z) funkciya berilgen bolsın.		S	betlikti ondaǵı

sızıqlar járdeminde S1, S2 ,...,Sn bólekshelerge ajratıp, onıń P = S1, S2 ,..., Sn bóleklewin payda qılamız. Bul bóleklewdıń diametrin p deymiz. Endi hár bir Sk

(k = 1,2,3,4,..., n) qálegen	( k , k , k ) noqatın alıp,	bul noqattaǵı funkciyanıń
mánisi f ( k , k , k ) ti Sk	nıń maydanı Sk ǵa kóbeytemiz hám
	n
	= f ( k , k , k ) Sk	(2)

k =1

qosındıńı dúzemiz. Qosındı f (x, y, z) funkciyaǵa, P bóleklewge hám ( k , k , k ) noqatqa baylanıslı boladı:

= ( f , P,( k , k , k )).

(2)qosındı f (x, y, z) funkciyanıń integral qosındısı (Riman qosındısı)

delinedi.

1-anıqlama. Eger 0 alǵanda hám sonday 0 tabılıp, S betliktıń diametrи p bolǵan hár qanday bóleklew ushın dúzilgen qosındı qálegen

( k , k , k ) SK noqatta

− J

340

teńsizlik orınlı bolsa, onda f (x, y, z) funkciya S betlik boyınsha integrallanıwshı delinip, J san bolsa f (x, y, z) funkciyanıń birinshi túr betlik integralı delinedi. Birinshi túr betlik integralı

f (x, y, z)ds

arqalı belgilenedi:

f (x, y, z)ds = lim f ( k , k , k ) Sk .

p →0 k =1

Birinshi

túr

betlik

integralı

betliktıń tárepine baylanıslı bolmaydı. Dara

f (x, y, z) = 1 bolsa, onda

ds = S

boladı.

Meyli

f (x, y, z) funkciya (1) teńleme menen berilgen S betlikte anıqlanǵan

bolsın.

1-teorema. Eger f (x, y, z)

funkciya S

betlikte úzliksiz bolsa, onda bul

funkciyanıń betlik boyınsha birinshi túr betlik integralı bar bolıp hám

f (x, y, z)ds = f (x, y, z(x, y)) 1 + zx2 (x, y) + z y2 (x, y)dxdy

(3)

boladı. Eger keńisliktegi S betlik x = x(y, z)

teńleme menen anıqlanǵan bolıp,

bunda

x = x(y, z)

funkciya

úzliksiz hám úzliksiz xy (y, z),

xz (y, z) dara

tuwındılarǵa iye bolsa, bul betlikte úzliksiz bolǵan f (x,

y, z) funkciyanıń birinshi

túr betlik integralı bar bolıp hám

f (x, y, z)dS =

f (x(y, z), y, z) 1 + xy2 (y,

z)+ xz

2 (y, z)dydz

(7)

boladı. Eger keńisliktegi S betlik y = y(z, x)

teńleme menen anıqlanǵan bolıp,

bunda

y = y(z, x)

funkciya

úzliksiz hám

úzliksiz yz (z, x),

yx (z, x) dara

tuwındılarǵa iye bolsa, bul betlikte anıqlanǵan úzliksiz f (x, y,

z) funkciyanıń

birinshi túr betlik integralı bar bolıp hám

341


f (x, y, z)dS = f (x, y(z, x), z)		1 + yz	2 (z, x)+ yx2 (z, x)dzdx	(8)
S	D

boladı.

Birinshi túr betlik integralları eki eseli integrallarǵa keltirilip, (3), (7) hám

(8) formulalar járdeminde esaplanadı.


1-mısal. J = 1 + 4x2		+ 4 y 2 dS integraldı esaplań, bunda S betlik
	S
		z =1 − x2 − y 2
betliktıń z = 0 tegislik penen kesilgen shekli bólegi.
◄ S betlik teńlemesi		z = z(x, y) kórinistegi betlik S : z =1 − x2 − y 2 (59-
sızılma).

59-sızılma

Berilgen integraldı (3) formuladan paydalanıp

		zx (x, y)= −2x,		z y (x, y)= −2 y
bolıp,

	1 + zx2 (x, y)+ z y2 (x, y) = 1 + 4x2 + 4 y 2
boladı. S betliktıń X 0Y tegisliktegi proekciyası D = (x, y) R2 : x2							+ y 2 1
boladı. (3) formuladan paydalanıp
					dxdy = (1 + 4x2 + 4 y2 )dxdy .
J =	1 + 4x2 + 4 y 2		1 + 4x2 + 4 y 2		dxdy = (1 + 4x2 + 4 y2 )dxdy .
D						D

Endi eki eseli integraldı esaplaymız

342

(1 + 4x2

x = r sin ,

0 2

+ 4 y2 )dxdy =

y = r cos ,

0 r 1

2 1

+ 4r 2 )rdr

2 r 2

+ r 4

d = 3 .

d =

Demek,

(1 + 4x2 + 4 y 2 )ds = 3 . ►

Birinshi túr betlik integralı eki eseli integral qáseytlerı arqalı qáseytlerge iye boladı.

Birinshi túr betlik integraldıń qollanılıwları. Birinshi túr betlik integralı járdeminde betliklerdıń maydanı, massalı betliktıń massası, awırlıq orayları, inerciya momentlerı tabıladı.

Anıqlamaǵa muapıq S = dS boladı.

		D
Meyli		S betlik boyınsha tıǵızlıq = (x, y, z)			bolǵan massa tarqatılǵan
bolsın. Bunday betliktıń massası
				m = (x, y, z)dS ,			(9)
				S
awırlıq orayıńıń koordinataları
xc =	1	x (x, y, z)ds , yc =	1	y (x, y, z)ds ,	zc =	1	z (x, y, z)ds
xc =	m S	x (x, y, z)ds , yc =	m	y (x, y, z)ds ,	zc =	m	z (x, y, z)ds
	m S		m	S		m	S

OX , OY , OZ kósherlerge qarata inerciya momentlerı

J x = (z 2 + y 2 ) (x, y, z)dS ,

J y = (z 2 + x2 ) (x, y, z)dS ,

J z = (x2 + y 2 ) (x, y, z)dS

boladı.

2-mısal. x = R2 − y2 − z2 yarım sfera boyınsha massa tarqalǵan bolıp, hár bir noqattaǵı tıǵızlıq usı noqattan koordinatalar basınasha bolǵan aralıqqa proporcianal. Massası tabılsın.

343

◄Shártke kóre

(x, y, z)= k (x2 + y 2 + z 2 )

boladı, bunda k -proporcianallıq korfficienti.

(9) formulaǵa kóre

m = k (x2 + y 2 + z 2 )dS

boladı, bunda S -joqarı yarım sfera. Meyli

(y, z)= −

, xz

(y, z)= −

− y2

− z 2

bolıp,

1 + xy2 (y, z)+ xz

2 (y, z) =

boladı. Nátiyjede

m = k (x2 +

teńlikke keltiremiz,

esaplaymız


y2 + z 2 )dS = k R2	R	dydz = kR3

S	x		D
bunda D = (y, z): y 2			+ z 2 R2 .

	1		dydz


	R2 − y2 − z 2
	R2 − y2 − z 2

Endi eki eseli integraldı

dydz

y = r cos , 0 2

− y2 − z 2

z = r sin , 0 r R

= −2 R (R2 − r 2 )−

d (R2

− r 2 ) d = −

1 (R2

Sonday qılıp massa m = 2kR 2 boladı.

2 R			rdr
									d =

			R	2	− r			2
	0 0		R		− r
1						R
						R

− r 2 )
− r 2 )		2	2				= 2 R .
	1
2						0
2						0

18.5. Ekinshi túr betlik integralları

Ekinshi túr betlik integralı túsinigi.

Meyli S betlikte f (x, y, z) funkciya berilgen bolsın. Bul betliktıń málim bir tárepin alıp, onıń

344

P ={S1, S2 ,...,Sn }

bóleklewin qaraymız. P bóleklewnıń hár bir Sk bólekshesine tiyisli bolǵan qálegen ( k , k , k ) noqatındaǵı funkciyanıń mánisi f ( k , k , k ) ni Sk nıń XOY tegisliktegi proekciyası Dk nıń maydanı Dk kóbeytip

= f ( k , k , k ) Dk

k =1

qosındıńı dúzemiz. Bul qosındı f (x, y, z) funkciyaǵa, P bóleklewge hám alınǵan

( k , k , k ) noqatlarǵa baylanıslı boladı.

1-anıqlama. Eger 0 san alǵanda hám sonday 0 san tabılıp, S betliktıń diametrı p bolǵan hár qanday P bóleklewnıń, hám hár bir Sk da alınǵan qálegen ( k , k , k ) lar ushın

− J

teńsizlik orınlı bolsa, onda f (x, y, z) funkciya S betliktıń tańlanǵan tárepi boyınsha integrallanıwshı delinip, J bolsa f (x, y, z) funkciyanıń S betliktnıń tańlanǵan tárepi boyınsha ekinshi túr betlik integralı delinedi. Onı

f (x, y, z)dxdy

arqalı belgilenedi. Demek,

		n
f (x, y, z)dxdy = lim		f ( k , k , k ) Dk .
S	p→0 k =1
Usıǵan uqsas
f (x, y, z)dydz ,		f (x, y, z)dzdx
S		S
ekinshi túr betlik integralları anıqlanadı.
Meyli S betlikte P(x, y, z) , Q(x, y, z) , R(x, y, z) funkciyalar berilgen bolıp,
P(x, y, z)dxdy ,	Q(x, y, z)dydz , R(x, y, z)dzdx
S	S	S

lar olardıń ekinshi túr betlik integralları bolsın.

P(x, y, z)dxdy + Q(x, y, z)dydz + R(x, y, z)dzdx

S S S

345

qosındı ekinshi túr betlik integraldıń ulıwma kórinisi delinedi. Onı

P(x, y, z)dxdy + Q(x, y, z)dydz + R(x, y, z)dzdx

arqalı belgilenedi:

P(x, y, z)dxdy + Q(x, y, z)dydz + R(x, y, z)dzdx =

= P(x, y, z)dxdy + Q(x, y, z)dydz + R(x, y, z)dzdx.

S	S	S
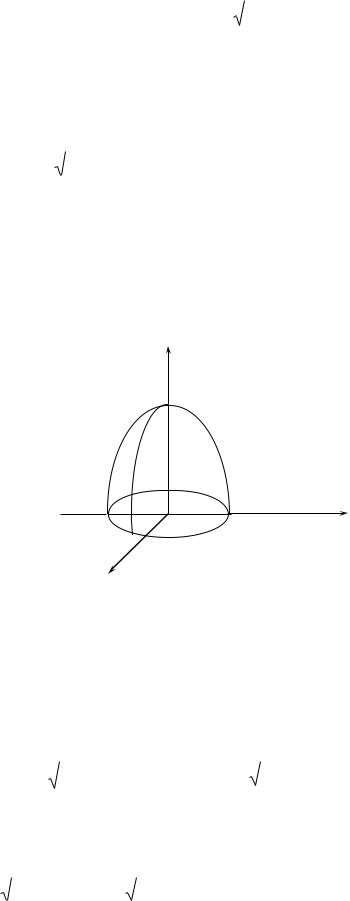
Meyli R3 keńislikte bazı bir V dene berilgen bolıp, onı orap turıwshı tuyıq
betlik sıypaq betlik bolsın. Bul betlikti S deymiz.
f (x, y, z) funkciya V	da anıqlanǵan bolsın. V deneni XOY tegisligine
parallel bolǵan tegislik eki V1	hám V2	bóleklerge ajratılsın. Deneni orap	túrǵan S
betlik hám S1 hám S2 betliklerge ajraladı. Meyli
f (x, y, z)dxdy + f (x, y, z)dxdy			(2)
S1		S12

integrallar qosındısı f (x, y, z) funkciyanıń tuyıq betlik boyınsha ekinshi túr betlik integralı delinedi. Onı

f (x, y, z)dxdy

arqalı belgilenedi. (2) qatnastaǵı birinshi integral S1 betliktıń ústki tárepi, ekinshi integral S2 betliktıń astınǵı tárepi boyınsha alınǵan. Usıǵan uqsas

f (x, y, z)dydz , f (x, y, z)dzdx

S S

hám ulıwma jaǵdayda

P(x, y, z)dxdy + Q(x, y, z)dydz + R(x, y, z)dxdz

integrallar anıqlanadı.

Ekinshi túr betlik integralınıń bar bolıwı hám onı esaplaw.

Meyli f (x, y, z) funkciya (1) teńleme menen berilgen S betlikte anıqlanǵan bolsın.

1-teorema. Eger f (x, y, z) funkciya S betlikte úzliksiz bolsa, onda bul funkciyanıń S betlik boyınsha ekinshi túr integralı bar bolıp hám

346

f (x, y, z)dxdy = f (x, y, z(x, y))dxdy		(3)
S	D
boladı. Usıǵan uqsas joqarıdaǵıday, tiyisli shártlerde
f (x,	y, z)dydz , f (x, y, z)dzdx
S	S
integrallar bar bolıp hám
f (x,	y, z)dydz = f (x(y, z), y, z)dydz	(6)
S	D
f (x,	y, z)dzdx = f (x, y(z, x), z)dzdx	(7)
S	D

boladı. Ekinshi túr betlik integralları eki eseli integrallarǵa keltirilip (3), (6) hám

(7)formulalar járdeminde esaplanadı.

1)Eger S betlik jasawshıları OZ kósherine parallel bolǵan cilindrlik betlik bolsa, onda

f (x, y, z)dxdy = 0

boladı.

2) jasawshıları OX kósherine parallel bolǵan cilindrlik betlik bolsa, onda

f (x, y, z)dydz = 0

boladı.

3) jasawshıları OZ kósherine parallel bolǵan cilindrlik betlik bolsa, onda

f (x, y, z)dzdx = 0

boladı.

1-mısal. Ekinshi túr betlik integralı (y 2 + z 2 )dxdy esaplań, bunda S betlik

z = a2 − x2 nıń y = 0 , y = b tegislikler arasındaǵı bóleginıń ústki tárepi (60sızılma).

347

	M	b
		b
0		Y

60-sızılma

◄ Betliktıń M noqattaǵı normalı OZ kósheri menen súyir múyesh p ayda etedi. Sonıń ushın berilgen integraldı (3) formulaǵa kóre esaplawda oń belgisi menen alındı. S betliktıń XOY tegisligine proekciyası

D = (x, y) R2 : − a x a, 0 y b

tórtmúyeshden ibarat boladı. (3) formuladan paydalanıp

(y2

+ z 2 )dxdy =

y 2 +

dxdy =

− x2

a b

a y3

y = b

(y2 + a2 − x2 )dy dx =

+ a2 y − x2 y

dx =

−a 0

−a 3

y = 0

a b3

ab(b2 + 2a2 ). ►

+ a2b − x2b dx =

x + a2bx −

− a

−b

Ekinshi túr betlik integralı eki eseli integralnıń qáseytlerıne uqsas qáseytlerge iye.

18.6. Stoks formulası

Keńislikеф

z = z(x, y)

(1)

348

(1) teńleme menen anıqlanǵan S betlikti qaraymız. Onıń XOY tegisliktegi proekciyası D kóplikti payda bolsın. S betlik hám D figura nıń shegaralawshı tuyıq sızıqlardı sáykes túrde S hám D deymiz. S nıń proekciyası D boladı.

Betlik tárepi hám konturı baǵıtları onıń proekciyaları baǵıtları arasındaǵı sáykeslik 62sızılmada keltirilgan.

x	D
	D

62-sızılma

Meyli (1) teńlemedegi z = z(x, y) funkciya D kóplikte úzliksiz hám úzliksiz

z x' (x, y), z 'y (x, y) dara tuwındılarǵa iye bolsın.

Meyli S betlikte P = P(x, y, z) funkciya anıqlanǵan bolıp, ol úzliksiz hám

úzliksiz

P(x, y, z)	,	P(x, y, z)	,	P(x, y, z)
x		y		z

dara tuwındılarǵa iye bolsın. Bunday holda P(x, y, z)dx iymek sızıqlı integral

bar boladı. Bunda S kontur baǵıttıń betlik tárepi menen sáykesligi 29-sızılmada keltirilgen.

349

<<< < Предыдущая 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 3435 / 3635 36 > Следующая >>>

Соседние файлы в предмете Дискретная математика

#
10.08.20242.46 Mб6Aniq integrallar.pdf
#
09.08.20243.06 Mб5Apiwayi differencialliq tenlemeler.pdf
#
09.08.20243 Mб7Differencialliq tenlemeler.pdf
#
09.08.20241.38 Mб17Joqari matematika paninen lekciyalar.pdf
#
09.08.20241.17 Mб11Matematika (Lekciya).pdf
#
10.08.20247.89 Mб15Matematikaliq analiz oqiw qollanba.pdf
#
10.08.20244.64 Mб17Matematikaliq analiz.pdf
#
10.08.20246.32 Mб73Matematikani oqitiw metodikasi.pdf
#
10.08.20241.7 Mб4Tenlemeler ham tensizlikler.pdf
#
10.08.20241.65 Mб3Tensizliklerdi dalillew usillari.pdf