Meyli AB iymek sızıq y = y(x) (a x b) teńleme menen berilgen bolıp, y(x) funkciya a, b úzliksiz, y'(x) tuwındıǵa iye bolsın. Onda (2) hám (5) formulalar tómendegi
|
|
|
b |
|
|
|
f (x, y)dx = f (x, y(x))dx, |
(6) |
|
|
|
|
|
|
|
AB |
a |
|
|
|
|
b |
|
|
P(x, y)dx + Q(x, y)dy = [P(x, y(x)) + Q(x, y(x))y (x)]dx |
(7) |
|
|
|
a |
|
|
AB |
|
|
|
|
|
|
|
|
kóriniske keledi. Meyli |
AB iymek sızıq x = x( y) (c y d ) teńleme menen |
|
|
berilgen bolıp, x = x( y) |
funkciya c, d да úzliksiz x' ( y) tuwındıǵa iye bolsın. |
|
Onda (4) hám (5) formulalar tómendegi |
|
|
|
|
d |
|
|
|
f (x, y)dy = f (x( y), y)dy , |
(8) |
|
|
|
|
|
|
|
AB |
c |
|
|
|
|
d |
|
|
P(x, y)dx + Q(x, y)dy = [P(x( y), y)x ( y) + Q(x( y), y)]dy |
(9) |
|
|
|
|
|
|
AB |
|
c |
|
|
kóriniske keledi. |
|
|
|
|
1-mısal. J1 = ( x2 − y2 )dx, J 2 |
= ( x2 − y2 )dy integrallar esaplań. Bunda |
|
AB |
|
AB |
|
AB |
|
iymek sızıq y = x 2 parabolanıń abcissaları x = 0, x = 2 bolǵan noqatları arasındaǵı bólegi.
|
|
|
|
|
|
|
|
|
◄ |
AB iymek sızıq y = x 2 |
teńleme menen anıqlanıp, J |
1 |
|
integraldı esaplawda |
|
|
|
|
|
|
|
|
(6) formuladan paydalanamız |
|
|
|
|
|
|
|
|
|
2 |
|
56 |
|
|
|
|
J1 = (x2 − y 2 )dx = (x2 − x4 )dx = − |
|
. |
|
|
15 |
|
|
AB |
0 |
|
|
|
|
|
|
|
|
|
|
|
J |
2 |
integralda integrallaw iymek sızıǵı x 2 = y bolıp, (8) formulaǵa kóre |
|
|
|
|
|
|
|
|
|
|
|
4 |
40 |
|
|
|
J 2 = (x2 − y 2 )dy = ( y − y 2 )dy = − |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
AB |
0 |
|
|
boladı. ►
2-mısal. y 2 dx + x2 dy integraldı esaplań, bunda AB iymek sızıq
AB
|
x2 |
+ |
y 2 |
=1 ellipstıń joqarı yarım tegisliktegi bólegi. |
|
a2 |
b2 |
|
|
|
|
|
|
◄Bul ellipstıń parametrlik teńlemesi |
|
|
|
|
x = a cost, |
|
|
|
|
|
|
|
|
|
y = b sint |
boladı. A = (a,0) noqatqa parametrdıń t = 0 mánisi, B = (−a,0) noqatqa t = mánisi sáykes kelip, t parametr 0 den ge ózgergende (x, y) noqat A dan B ǵa qarap ellipstıń joqarı yarım tegisliktegi bólegin sızadı.
Meyli P(x, y) = y2 ,Q(x, y) = x2 funkciyalar |
|
úzliksiz. Berilgen integraldı |
AB |
(5) formuladan paydalanıp esaplaymız
y2dx + x2dy = [b2 sin2 t (−asint) + a2 cos2 t bcost]dt = |
|
|
|
|
|
AB |
0 |
|
|
|
|
|
4 |
|
|
|
= ab (a cos3 t − bsin3 t)dt = − |
ab2 |
. ► |
|
3 |
|
0 |
|
|
Ekinshi túr iymek sızıqlı integraldıń bazı bir qollanıwları. Ekinshi túr iymek sızıqlı integrallar járdeminde tegis figuranıń maydanı, kúsh tásirinde bolǵan maydanda orınlanǵan jumıs tabıladı hám basqa túrli fizikalıq hám mexanikalıq máseleler sheshiledi. Tegislikte bazı bir maydanǵa iye bolǵan D figura berilgen bolıp, onıń shegarası tuwrılanıwshı tuyıq D sızıqtan ibarat bolsın. Bul figuranıń maydanı
|
D = xdy , |
D = − ydx |
D = |
1 |
xdy − ydx |
(10) |
|
2 |
|
D |
|
|
D |
|
D |
|
|
|
|
|
|
|
|
formulalar járdeminde tabıladı. |
|
|
|
|
|
|
|
|
Meyli uzınlıqqa iye bolǵan |
iymek sızıq berilgen bolıp, onıń hár bir |
|
AB |
|
(x, y) noqatı |
|
|
|
|
|
|
|
|
→ |
|
|
→ |
→ |
|
|
|
|
F (x, y) = P(x, y) i + Q(x, y) j |
|
|
|
kúsh tásirinde bolsın. Onda A noqatı B noqatqa ótkiziwde orınlanǵan jumıs
51-sızılma
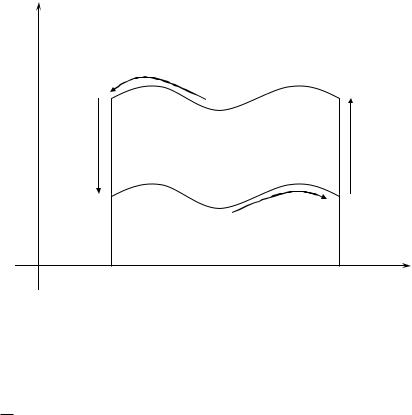
Meyli D1 shegarası D1 - I, II, III, IV sızıqlarǵa ajraladı (bunda sızıqlar noqatlarǵa aylanıw múmkin).
Meyli D = D1 D1 da P(x, y) funkciya úzliksiz bolıp, ol úzliksiz
dara tuwındıǵa iye bolsın. P(x, y)dx iymek sızıqlı integraldı qaraymız.
D1
P(x, y)dx = P(x, y)dx + P(x, y)dx + P(x, y)dx + P(x, y)dx
D1 I II III IV
alamız. hám V sızıqlar OX kósherine perpendikulyar bolǵanlıǵı sebebli
P(x, y)dx = P(x, y)dx = 0
|
II |
|
IV |
|
|
bolıp, |
|
|
|
|
|
|
P(x, y)dx = P(x, y)dx + P(x, y)dx |
|
D1 |
I |
III |
|
|
boladı. Endi |
|
|
|
|
|
P(x, y)dx + P(x, y)dx = b P(x, y1 (x))dx + b P(x, y2 (x))dx = |
I |
III |
|
a |
a |
|
b |
|
b |
|
y= y2 |
|
= P(x, y1 ) − P(x, y2 ) dx = − P(x, y) |
|
|
|
|
|
y= y1 dx = |
|
|
|
a |
|
a |
|
|
b y=y2 |
P(x, y) |
|
|
P(x, y) |
|
= − |
|
y |
dy dx = − |
y |
dxdy |
a y=y |
|
D |
|
|
1 |
|
|
1 |
|
|
bolsa, onda
P(x, y)dx − |
P(x, y) dxdy |
(1) |
D1 |
D1 |
y |
|
|
|
теńlikke iye bolamız. |
|
|
|
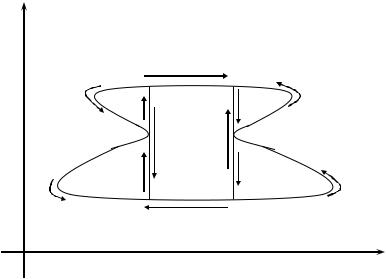
Meyli tegisliktegi G kóplik sonday bolsınкi, onı joqarıdaǵı D1 |
arqalı Gk |
(k =1,2,3...) ajratıw múmkin bolsın. (52-sızılma) |
|
y
G1
G3
G2
52-sızılma
Bunday kóplik ushın hám (1) formula orınlı boladı:
|
n |
|
n |
|
|
|
|
P(x, y)dx = |
P(x, y)dx = |
|
− |
P(x, y)dxdy |
G1 |
k =1 |
Gk |
|
|
|
y |
|
k =1 Gk |
|
|
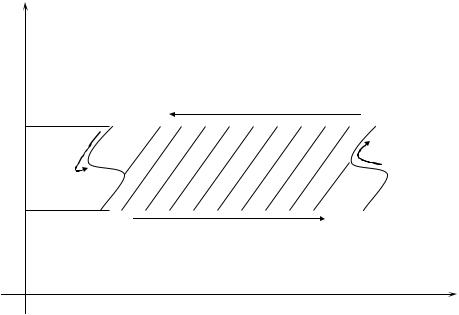
Endi tegislikte x = x1 ( y), x = x2 ( y) , (c y d ) hám y = c, y = d sızıqlar menen shegaralanǵan D2 kóplikti alayıq, bunda x1 ( y) , x2 ( y) funkciyalar [c,d] da
úzliksiz. (53-sızılma)
y
d |
|
|
|
|
|
|
|
IV |
|
|
x = x2 |
(y) |
|
|
|
|
|
|
|
I |
|
|
|
x = x1(y) |
D2 |
|
|
|
|
II |
III |
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
x |
|
|
|
|
53-sızılma |
|
Meyli D2 shegarası D2 |
- I, II, III, IV sızıqlarǵa ajraladı (bunda |
hám V |
sızıqlar noqatlarǵa aylanıw múmkin). |
|
|
|
|
|
|
Meyli D2 = D2 D2 |
da Q(x, y) funkciya úzliksiz bolıp, ol |
úzliksiz |
Q(x, y) |
dara tuwındıǵa iye bolsın. |
Q(x, y)dy iymek sızıqlı integraldı qaraymız. |
x |
|
|
G2 |
|
|
|
|
|
|
Q(x, y)dy = Q(x, y)dy + Q(x, y)dy + Q(x, y)dy + Q(x, y)dy |
G2 |
I |
II |
III |
IV |
jazıp alamız. |
hám V sızıqlar OY kósherine perpendikulyar bolǵanlıǵı sebebli |
|
|
|
Q(x, y)dy = Q(x, y)dy = 0 |
|
|
|
|
II |
IV |
|
bolıp, |
|
|
|
|
|
|
|
Q(x, y)dy = Q(x, y)dy + Q(x, y)dy |
|
|
|
G2 |
I |
III |
|
boladı. Endi
Q(x, y)dy + Q(x, y)dy = d Q(x1(y), y)dy +
+ d Q(x2 (y), y)dy = d Q(x1 , y)− Q(x2 , y) dy =
d |
|
x=x2 |
|
d |
Q(x, y) |
|
|
|
Q(x , y) |
|
= Q(x, y) |
|
dy = |
dx |
dy = |
dxdy |
|
x=x |
|
|
x |
|
|
x |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
c |
|
|
|
|
c |
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
esapqa alıp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q(x, y)dy = Q(x, y) dxdy . |
|
(2) |
|
|
|
|
|
G2 |
|
D2 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
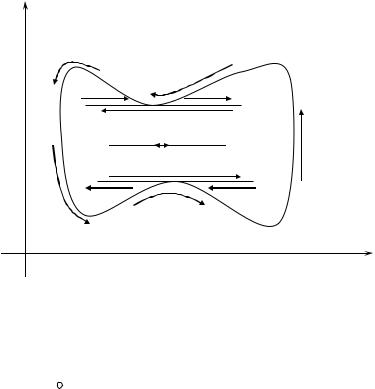
Meyli tegisliktegi |
F |
kóplik |
sonday |
bolıp, |
onı |
(gorizontal sızıqlar |
járdeminde) joqarıdaǵı D2 arqalı Fk |
(k = 1,2,3...) larǵa ajratıw múmkin bolsın. |
(54sızılma) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y
0 x
54sızılma
Bunday kóplik ushın hám (2) formula orınlı boladı
|
n |
|
n |
|
|
|
|
|
Q(x, y)dxdy |
Q(x, y)dy = |
Q(x, y)dy = |
|
|
Q(x, y)dxdy |
= |
F |
k =1 |
Fk |
|
|
|
x |
|
G |
x |
k =1 Fk |
|
|
|
Meyli tegisliktegi D kóplik joqarıdaǵı D1 |
hám D2 |
qáseytke iye bolıp, onda |
P(x, y), Q(x, y) funkciyalar úzliksiz hám |
úzliksiz |
P(x, y) |
, |
Q(x, y) |
dara |
|
|
y |
|
x |
|
tuwındılarǵa iye bolsın. Onda P(x, y) hám Q(x, y) funkciyalar ushın (1) hám (2) formulalar orınlı boladı. Olardı aǵzama-aǵza qossaq
|
P(x, y)dx + Q(x, y)dy = |
|
Q(x, y) |
− |
P(x, y) |
(3) |
|
|
|
|
|
|
x |
y |
dxdy . |
D |
|
D |
|
|
|

Bul Grin formulası delinedi. Demek, Grin formulası kóplik boyınsha alınǵan eki eseli integral menen sol kóplik shegarası boyınsha alınǵan iymek sızıqlı integraldı baylanısın ańlatadı.
Grin formulasınıń bazı bir bir qollanıwları. Meyli joqarıda keltirilgen bir baylamlı D kóplikte P(x, y), Q(x, y) funkciyalar úzliksiz hám úzliksiz dara
tuwındılarǵa iye bolsın. Onda Grin formulası (3) orınlı boladı.
Grin formulasınan paydalanıp , tegis figuranıń maydanınıń iymek sızıqlı integral járdeminde ańlatılıwı, yakobiannıń geometriyalıq mánisin hám bazı bir tastıyıqlawlarnıń ekvivalentligin kórsetiw múmkin.
1) Tegis figura maydanınıń iymek sızıqlı integral arqalı ańlatılıwı. Meyli
P* (x, y), Q* (x, y) funkciyalar |
|
D |
|
kóplikte joqarıda keltirilgen |
shártlerin |
qanaatlandırıwı menen birge |
|
|
|
|
|
|
|
|
|
|
|
|
|
Q (x, y) |
− |
P (x, y) |
1 |
|
|
|
|
x |
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
shártti qanaatlandırsın. Onda |
|
|
|
|
|
|
|
|
|
|
|
|
|
Q* (x, y) |
− |
P* (x, y) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
y |
dxdy = D |
|
|
|
D |
|
|
|
|
|
|
|
|
bolıp, Grin formulasına kóre |
|
|
|
|
|
|
|
|
|
|
|
|
|
D = P* (x, y)dx +Q* (x, y)dy |
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
boladı. Dara jaǵdayda P* (x, y) = −y, Q(x, y) = 0 yamasa P* (x, y) = 0, |
Q(x, y) = x |
yamasa P* (x, y) = − |
1 |
y, Q(x, y) = |
1 |
x bolsa, onda |
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
Q (x, y) |
− |
P (x, y) |
1 |
|
|
|
|
x |
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
bolıp, kópliktıń maydanı |
|
|
|
|
|
|
|
|
|
|
|
|
|
D = − ydx = xdy = |
1 |
xdy − ydx |
(4) |
|
|
|
|
|
|
D |
|
|
|
D |
2 |
D |
|
|
|
|
|
|
|
|
|
|
|
|
boladı.
2) Yakobiannıń geometriyalıq mánisi. Meyli XOY tegislikte D kóplik berilgen bolıp, onıń shegarası D bolsın. (55-sızılma). UOV tegislikte kóplik berilgen bolıp, onıń shegarası bolsın. (56-sızılma).
0 x 0 u
55-sızılma |
56-sızılma |
Meyli D hám kóplik noqatları arasında óz-ara bir mánisli sáykeslik |
ornatılǵan bolıp, olar |
|
|
x = x(u,v), |
|
|
|
y = y(u,v) |
formula menen ańlatılsın. Bunda |
x(u,v), y(u,v) funkciyalar tuyıq kóplikte |
úzliksiz hám úzliksiz dara tuwındılarǵa iye bolsın. kóplik shegarası sızıq
|
|
|
|
|
u = u(t), |
(t1 t |
t2 ) |
|
|
|
|
v = v(t) |
|
|
|
parametrlik teńleme menen ańlatılsın. Bunda u(t), v(t) funkciyalar [t1,t2 ] |
aralıqta |
úzliksiz hám úzliksiz tuwındılarǵa iye. Onda D kópliktıń shegarası D |
|
x = x(u(t),v(t)) = x(t), |
(t1 t t2 ) |
|
|
|
|
|
y = y(u(t),v(t)) = y(t) |
|
|
teńlemeler sisteması menen |
anıqlanadı. Bunda nıń noqatlarǵa |
D nıń |
noqatları sáykes keledi. Bizge belgili |
|
|
|
|
D = xdy . |
|
(5) |
|
|
D |
|
|
Bul teńliktıń oń tárepindegi integral ushın
|
|
t2 |
dy |
t2 |
y |
|
xdy = x |
|
dt = x |
|
|
dt |
u |
|
D |
t |
t |
|
|
|
1 |
|
1 |
|
|
boladı. ( t parametr t1 dan t2 ǵa qarap ózgergende D iymek sızıq oń baǵıtta bolsa, onda iymek sızıqtıń baǵıtı oń hám teris hám bolıwı múmkin. Sonıń ushın
bir-birinen belgi menen parq qıladı. Eger D oń baǵıtına nıń oń baǵıtı sáykes kelse, onda « + » belgi alınadı, keri jaǵdayda «-» belgi alınadı.)
Grin formulasınan paydalanıp
|
y |
|
|
|
y |
|
|
|
|
|
|
y |
|
|
|
|
y |
|
x |
u |
du + |
v |
dv |
= |
|
x |
|
|
|
− |
|
|
|
x |
dudv = |
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
v |
|
v |
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
x |
|
|
|
(7) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
y |
|
|
x |
|
y |
|
|
|
u |
v |
|
= J (u ,v)dudy. |
= |
|
|
|
− |
|
|
|
|
dudy = |
|
|
|
|
|
|
|
|
u |
|
v |
|
|
v |
|
u |
|
|
|
y |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
v |
|
|
|
|
(5), (6) hám (7) teńliklerden
D = J (u,v)dudv
kelip shıǵadı. Orta mánisi haqqında teoremańa kóre
J (u,v)dudv = J ( , )
boladı. Demek,
D = J ( , )
bolıp, onnan
J ( , ) = D
bolıwın tabamız.