Matematikaliq analiz oqiw qollanba
.pdf
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 1 + |
|
h2 |
|
|
x 2 |
+ |
h2 |
|
x 2 |
= 1 + |
h2 |
|
|
|||||
|
1 + (z 2 ( |
k |
, |
k |
))2 + (z 2 ( |
k |
, |
k |
))2 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
x |
|
|
|
y |
|
|
|
|
|
|
|
|
r 2 x 2 + y 2 |
|
r 2 x 2 + y 2 |
|
r 2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
bolsa, onda |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
S = |
1 + |
h |
dxdy = |
1 + |
h |
|
|
dxdy = r |
r 2 + h2 |
|
|
|
|
|||||||||||||||
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
D |
|
|
|
x |
|
|
|
|
|
|
|
|
|
x |
|
|
D |
|
|
|
|
|
|
|
|
|
boladı. ► |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Eki eseli integraldıń mexanikada qollanıwları |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
Meyli |
|
tegislikte |
massaǵa iye |
bolǵan materiallıq |
D figuranıń hár |
bir |
|||||||||||||||||||||||||
(x, y) D |
noqatında tıǵızlıǵı (x, y) |
bolıp, ol D úzliksiz bolsın. D figuranıń |
||||||||||||||||||||||||||||||
massasın tabamız. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Eger |
|
(x, y) = c − const |
|
bolsa, onda |
|
|
D figuranıń massası m = C D teń |
||||||||||||||||||||||||
boladı. Eger |
(x, y) |
qálegen |
|
(k =1,2,..n) |
|
|
úzliksiz |
funkciya bolsa, onda |
D |
|||||||||||||||||||||||
figuranıń massasın tabıw ushın D nıń P ={D1, D2 ,..., Dn } bólekleniwi hám hár bir
Dk da (k =1,2,..n) qálegen ( k , k ) |
noqatın alamız ( k , k ) Dk . Hár bir Dk da |
|
(x, y) turaqlı hám onı ( k , k ) ǵa teń bolsa, onda Dk |
nıń massası ( k , k ) Dk |
|
ǵa teń bolıp, D figuranıń massası |
|
|
|
n |
|
|
( k , k ) Dk |
(7) |
k =1
teń boladı. P bólekleniwdıń diametri p → 0 da (7) qosındıniń limiti D figuranıń massasın ańlatadı. (7) qosındı (x, y) funkciyanıń integral qosındısı hám (x, y) funkciya D úzliksiz bolǵanlıǵı sebebli bul qosındıniń limiti
(x, y)dxdy
D
boladı. Demek, D figuranıń massası
m = (x, y)dxdy |
(8) |
D |
|
teńlik penen anıqlanadı.
4-mısal. Tegislikte a radiuslı dóńgelekli plastinka berilgen bolıp , onıń hár bir A(x, y) noqattaǵı tıǵızlıǵı usı noqattan koordinatalar basına shekem bolǵan aralıq proporcional. Dóńgelekli plastinkanıń massasın tabıń.
320
◄ Dekart koordinatalar sistemasınıń koordinatalar basına dóńgelekli
plastinkanıń orayın jaylastıramız. Onda |
plastinkanıń A(x, y) noqatınan |
||
|
|
|
|
koordinatalar basına shekem bolǵan aralıq d = |
|
x2 + y2 bolıp, plastinka tıǵızlıǵı |
|
(x, y)= k 
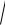x2 + y2
boladı, bunda k – proporcionallıq koefficenti. (8) formulaǵa kóre plastinka massası
m = k 
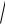x2 + y 2 dxdy
D
boladı, bunda D = (x, y) R2 : x2 + y 2 r 2 . Eki eseli integralda
x = r cos ,
x = r sin almastırıwdı orınlap, onı esaplaymız
|
|
|
|
|
2 a |
|
2 r 3 a |
2 |
|
|
|||||
|
|
|
x2 + y2 dxdy = |
k a3 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
m = |
|
k |
|
|
|
k r rdr d = k |
|
3 |
|
d = |
3 |
. ► |
|||
|
D |
|
|
|
0 |
0 |
|
0 |
|
0 |
|
|
|||
Eki eseli integrallar járdeminde statistikalıq momentler
M x |
= yp(x, y)dxdy , (Ox kósherine qarata), |
|||||
|
|
D |
|
|
|
|
M y = xp(x, |
y)dxdy , (Oy kósherine qarata) |
|||||
|
|
D |
|
|
|
|
awırlıq orayınıń koordinataları |
|
|
|
|
||
x0 |
= |
1 |
D xdxdy , y0 = |
1 |
D ydxdy , |
|
dxdy |
dxdy |
|||||
|
|
D |
|
|
D |
|
inerciya momentleri |
|
|
|
|
|
|
J x = y 2 p(x, y)dxdy , (Ox kósherine qarata), |
||||||
|
D |
|
|
|
|
|
J y |
= x2 p(x, |
y)dxdy , (Oy kósherine qarata) |
||||
|
D |
|
|
|
|
|
J 0 = (x2 + y 2 )p(x, |
y)dxdy (koordinatalar basına qarata) |
|||||
D |
|
|
|
|
|
|
tabıladı.
321
18-§. IYMEK SIZIQLI HÁM BETLIK INTEGRALLAR
18.1. Birinshi túr iymek sızıqlı integrallar
Birinshi túr iymek sızıqlı integral túsinigi. Tegislikte ápiwayı uzınlıqqa
iye bolǵan AB iymek sızıqtı qaraymız. (47-sızılma)
y
B
|
|
|
Ak +1 |
|
|
A2 |
Ak |
|
|
|
|
A |
A1 |
|
xk |
|
|
0 |
x |
|
47-sızılma
Bul iymek sızıqta А dan В ǵa qarap baǵıtı oń baǵıt dep, onıń
A0 , A1 ,..., An−1 , An ( A0 = A, An = B)
noqatlar járdeminde payda bolǵan |
P ={A0 , A1,..., An−1, An } bólekleniwin alamız. |
|||
|
|
|
|
|
Nátiyjede |
AB |
iymek sızıq Ak Ak +1 |
(k = 0,1,2,...,n −1) bóleklerge ajraladı. Onıń |
|
uzınlıǵın |
Sk |
(k = 0,1,2,..., n −1) bolsa P bóleklewdıń diametri p |
= max{ Sk } |
|
|
|
|
|
k |
boladı. |
|
|
|
|
|
|
|
||
Meyli AB iymek sızıqta f (x, y) funkciya anıqlanǵan bolsın. (( x, y) AB). |
||||
|
|
|
|
|
Hár bir Ak Ak +1 |
qálegen ( k , k ) noqattı alıp, soń bul noqattaǵı f (x, y) |
funkciyanıń |
||
mánisi f ( k , k ) Sk kóbeytip
n−1
= f ( k , k ) Sk
k =0
qosındını payda etemiz.
322
|
|
|
|
|
|
|
|
|
|
|
Anıqlama. Eger |
0 |
alǵanda |
|
sonday 0 san tabılıp, |
AB iymek |
|||||
sızıqtıń diametri p |
bolǵan hár qanday P bóleklew ushın dúzilgen qosındı |
|||||||||
qálegen |
|
|
noqatlarda |
|
|
|
|
|
||
( k , k ) Ak Ak +1 |
|
|
|
|
|
|||||
|
|
|
|
|
− J |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
teńsizlik |
orınlı bolsa, |
onda |
f (x, y) |
|
funkciya |
|
iymek sızıq |
boyınsha |
||
|
AB |
|||||||||
integrallanıwshı dep, |
J |
sanı |
f (x, y) funkciyanıń |
|
iymek sızıq boyınsha |
|||||
AB |
||||||||||
birinshi túr iymek sızıqlı integralı delinedi. Ol
f (x, y)ds
AB
arqalı belgilenedi. Demek
f (x, y)ds = lim n−1 f ( k , k ) Sk .
p →0 k =0
AB
Birinshi túr iymek sızıqlı integralı AB iymek sızıqtıń baǵıtına baylanıslı bolmaydı.
|
f (x, y)ds = f (x, y)ds . |
|
|
AB |
BA |
Birinshi túr iymek sızıqlı integraldıń bar bolıwı hám onı esaplaw.
Birinshi túr iymek sızıqlı integraldıń anıqlamasınan kórinip tur, ol berilgen f (x, y)
funkciya hám AB iymek sızıqqa baylanıslı boladı.
|
|
Meyli AB ápiwayı sıypaq iymek sızıq |
|
x = x(t), |
( t ) |
|
|
y = y(t) |
|
teńlemeler sistemasi menen anıqlanǵan hám
A = (x( ), y( )), B = (x( ), y( ))
bolsın. Usı iymek sızıqta f (x, y) funkciya berilgen.
Teorema. Eger f (x, y) funkciya AB úzliksiz bolsa, onda birinshi túr iymek
sızıqlı integral
f (x, y)ds
AB
323
bar bolıp,
|
|
|
|
|
|
|
|
|
|
f (x, y)ds = f (x(t), y(t)) x 2 (t) + y 2 (t)dt |
|
||||||
|
|
|
|
|
||||
|
AB |
|
|
|||||
boladı. |
|
|
|
|
|
|
|
|
Bul teorema birinshi túr iymek sızıqlı integraldıń bar bolıwın ańlatıw menen |
||||||||
birge onı esaplaw imkanın beredi. |
|
|||||||
1-saldar. Meyli |
|
iymek sızıq y = y(x) (a x b) |
teńleme menen |
|||||
AB |
||||||||
anıqlanǵan bolıp, |
y(x) |
funkciya [a,b] úzliksiz hám úzliksiz y (x) tuwındıǵa iye |
||||||
|
|
|
|
|
|
|
|
|
bolsın ( y(a)= A , |
y(b)= B ). |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Eger f (x, y) funkciya |
AB iymek sızıqta úzliksiz bolsa, onda f (x, y)ds |
|||||||
|
|
|
|
|
|
|
|
AB |
birinshi túr iymek sızıqlı integral bar bolıp |
|
|||||||
|
|
|
b |
|
|
|
||
|
|
|
|
|
||||
|
|
f (x, y)ds = f (x, y(x)) 1 + y 2 (x)dx |
(4) |
|||||
|
|
|
|
|
|
|
|
|
|
|
AB |
a |
|
||||
boladı.
|
|
|
|
|
|
|
|
|
|
2-saldar. Meyli AB iymek sızıq poliyar koordinatalar sistemasında |
|||||||||
|
|
|
= ( ) |
( ) |
|
||||
teńleme menen anıqlanǵan bolsın, bunda = ( ) funkciya [ , ] |
segmentte |
||||||||
úzliksiz hám úzliksiz tuwındıǵa iye bolsın. Bul iymek sızıqta f (x, y) |
funkciya |
||||||||
anıqlanǵan hám úzliksiz. Onda |
f (x, y)ds |
birinshi túr iymek sızıqlı integral bar |
|||||||
|
|
|
|
AB |
|
|
|
|
|
bolıp |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x, y)ds = f ( cos , sin ) 2 + 2 d |
(5) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
AB |
|
|
|
|
|
||
boladı. |
|
|
|
|
|
|
|||
|
x |
|
|
|
|
|
|||
1-mısal. J = |
ds |
integraldı esaplań, bunda AB iymek sızıq y 2 |
= 2x |
||||||
|
|||||||||
AB y
parabolanıń (1, 
2), (2, 2) noqatları arasındaǵı bolegi.
◄ (4) formuladan paydalanıp
324
|
|
|
|
|
|
|
J = x |
|
|
1 + ( 2x ) |
2 |
dx . |
|||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
1 |
+ 2 |
x |
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
(5 |
|
|
|
). ► |
|||||
J = |
|
|
|
dx = |
|
|
|
1 + 2xdx = |
5 |
− 3 |
3 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||
1 |
|
2x |
|
|
|
|
2x |
2 |
|
1 |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
||||||
Birinshi túr iymek sızıqlı integrallardıń bazı bir qollanıwları. Birinshi túr iymek sızıqlı integrallar járdeminde iymek sızıqtıń uzınlıǵın, denenıń massasın, awırlıq orayın, inerciya momentlerin tabıw arqalı máseleler sheshiledi.
1. Tegislikte uzınlıqqa iye bolǵan AB iymek sızıqtıń uzınlıǵı
|
|
|
|
|
S = ds, |
|
|
|
(6) |
|
|
|
|
|
|
AB |
|
|
|
|
|
integral járdeminde tabıladı. |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||
2. Tegislikte uzınlıqqa iye bolǵan |
AB iymek sızıǵı boyınsha massa |
|||||||||
tarqatılǵan bolıp, onıń tıgızlıǵı = (x, y) |
bolsın. Bul iymek sızıqtıń massası |
|||||||||
|
|
|
|
|
m = (x, y)ds, |
|
|
|
(7) |
|
|
|
|
|
|
AB |
|
|
|
|
|
awırlıq orayınıń koordinataları bolsa |
|
|
|
|
|
|||||
|
x0 = |
1 |
|
x (x, y)ds, |
y0 = |
1 |
y (x, y)ds |
(8) |
||
|
|
|
||||||||
|
|
m AB |
|
|
|
m AB |
|
|||
integrallar járdeminde tabıladı. |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||
3. Tegislikte uzınlıqqa iye bolǵan |
AB iymek sızıqtıń Ox |
hám Oy |
||||||||
koordinata kósherine qarata statistikalıq momentlerı |
|
|||||||||
|
|
|
|
|
Sx = yds, |
S y = xds |
(9) |
|||
|
|
|
|
|
AB |
|
|
|
AB |
|
formula menen sol kósherge qarata inerciya momentlerı bolsa |
|
|||||||||
|
|
|
|
|
J x = y2 ds, |
J y = x2 ds |
(10) |
|||
|
|
|
|
|
AB |
|
|
|
AB |
|
integrallar járdeminde tabıladı. |
|
|
|
|
|
|||||
x(t) = a cos3 t, |
(0 t 2 ) teńlemeler sisteması menen anıqlanǵan |
|||||||||
3-mısal. |
y(t) = a sin3 t |
|
||||||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
AB iymek sızıqtıń uzınlıǵın tabıń.
◄ (6) formulalarıdan paydalanıp
325
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
dt =2 |
|
|
|
||
S = ds = 4 |
x 2 (t) + y 2 (t) |
(−3a cos2 t sin t)2 + (3a sin2 t cost)2 dt = |
|||||||
|
|
|
|
|
|
|
|
|
|
AB |
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 4 2 |
9a2 |
sin2 2tdt =6a 2 sin 2tdt = 6a . ► |
|||||
|
|
4 |
|
||||||
|
|
0 |
|
|
|
0 |
|
||
Eskertiw. Meyli AB iymek sızıq keńisliktiń iymek sızıǵı bolıp, bul sızıqta
f (x, y, z) funkciya berilgen bolsın. Joqarıdaǵıday f (x, y, z) funkciyanıń AB iymek sızıq boyınsha birinshi túr iymek sızıqlı integral túsinigi kiritiledi hám úyreniledi.
18.2. Ekinshi túr iymek sızıqlı integral
Tegislikte (ápiwayı) uzınlıqqa iye bolǵan AB iymek sızıqtı qaraymız (48sızılma)
у
В
A |
Ak +1 |
|
2 |
|
|
yk +1 |
Ak |
|
yk |
||
|
||
A1 |
|
|
А |
xk |
|
|
|
|
xk |
xk +1 |
х |
|
|
|
48-sızılma |
|
|
|
Bul iymek sızıqtıń bazı bir P = A0 , A1, A2 ,..., An ,( A0 = A, An |
= B) |
bólekleniwin |
|||
|
|
|
|
|
|
alamız. Nátiyjede |
AB |
iymek sızıq Ak Ak +1 |
(k = 0,1,2,...n −1) |
bólekshelerge |
|
|
|
|
|
|
ajraladı. Ak Ak +1 nıń OX hám OY koordinatalar kósherlerdegi proekciyaları sáykes |
||||
túrde xk |
hám yk bolsın: |
|
|
|
|
|
|
|
|
|
прox Ak Ak +1 = xk , |
прoy Ak Ak +1 |
= yk |
(k = 0,1,2,...n −1). |
326
|
|
Meyli AB iymek sızıqta f (x, y) funkciya berilgen bolsın. Hár bir Ak Ak +1 da |
|
qálegen ( k , k ) noqatlarnı alıp, soń bul noqattaǵı funkciyanıń mánisi f ( k , k ) |
|
xk hám yk larǵa kóbeytip |
|
n−1 |
n−1 |
1 = f ( k , k ) xk , 2 = f ( k , k ) yk |
|
k =0 |
k =0 |
qosındılardı payda etemiz. Bul qosındılar |
f (x, y) funkciyaǵa baylanıslı bolıwı |
|
|
menen birge AB iymek sızıqtı bóleklewge hám hár bir Ak Ak +1 alınǵan ( k , k ) |
|
noqatlarǵa baylanıslı boladı. |
|
|
|
1-anıqlama. Eger 0 alǵanda, |
sonday 0 san tabılıp, AB iymek |
sızıqtıń diametri p bolǵan hár qanday |
P bóleklew ushın dúzilgen 1 ( 2 ) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
qosındı qálegen ( k , k ) Ak Ak +1 |
|
noqatlarda |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
1 − J1 |
|
( |
|
2 − J 2 |
|
) |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
teńsizlik orınlı bolsa, onda |
f (x, y) funkciya |
AB iymek sızıq boyınsha integral- |
||||||||||||||||||||
lanıwshı, J1 san ( J2 san) bolsa |
|
f (x, y) funkciyanıń ekinshi túr |
iymek sızıqlı |
|||||||||||||||||||
integralı delinedi. Ol |
f (x, y)dx, |
|
|
( f (x, y)dy) arqalı belgilenedi. Demek, |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AB |
|
|
|
|
|
AB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
n−1 |
|
|
|
|
||
|
lim |
k |
|
k |
|
|
k |
|
|
|
|
|
|
lim |
k |
k |
|
k |
||||
|
f (x, y)dx = |
|
f ( |
, |
) x |
, |
|
|
f (x, y)dy = |
|
f ( |
, ) y |
|
|||||||||
AB |
|
p →0 k =0 |
|
|
|
|
|
|
|
AB |
|
|
|
|
p →0 k =0 |
|
|
|
|
|||
Keltirilgen anıqlamadan tómendegi kelip shıǵadı:
|
|
|
1) f (x, y) funkciyanıń AB iymek sızıq boyınsha ekinshi túr iymek sızıqlı |
||
integralı ekew boladı: |
|
|
|
f (x, y)dx, |
f (x, y)dy . |
|
|
|
|
AB |
AB |
|
|
hám Q(x, y) funkciyalar berilgen bolıp , |
Meyli |
AB iymek sızıǵında P(x, y) |
|
P(x, y)dx, |
Q(x, y)dy lar bolsa olardıń ekinshi túr iymek sızıqlı integralları |
|
AB |
AB |
|
bolsın. Bul |
|
|
|
P(x, y)dx + |
Q(x, y)dy |
|
|
|
|
AB |
AB |
327
qosındı ekinshi túr iymek sızıqlı integraldıń ulıwma kórinisi delinedi hám
|
P(x, y)dx + Q(x, y)dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
AB |
|
|
|
|
|
arqalı belgilenedi: |
|
|
|
|
|
|
|
P(x, y)dx + Q(x, y)dy = |
P(x, y)dx + |
Q(x, y)dy . |
|
|
|
|
AB |
AB |
AB |
|
|
|
2) f (x, y) funkciyanıń ekinshi túr iymek sızıqlı |
integralları |
|
iymek |
|||
AB |
||||||
sızıqtıń baǵıtına baylanıslı bolıp, |
|
|
|
|
|
|
|
f (x, y)dx = − f (x, y)dx , |
f (x, y)dy = − |
f (x, y)dy |
|
|
|
|
|
|
|
|
|
|
BA |
AB |
BA |
|
AB |
|
|
boladı.
3) Eger AB iymek sızıq OX koordinatalar kósherine (OY koordinatalar kósherine) perpendikulyar bolǵan tuwrı sızıq kesimnen ibarat bolsa
|
f (x, y)dy = 0 |
|
|
|
|
f (x, y)dy = 0 |
|||
|
BA |
|
AB |
|
|
|
|
|
|
boladı. |
|
|
|
|
|
|
|
|
|
Meyli |
AB keńislikte ápiwayı uzınlıqqa iye bolǵan iymek sızıq bolıp, bul |
|||
iymek sızıqta |
f (x, y, z) funkciya berilgen bolsın. f (x, y, z) funkciyanı ekinshi túr |
|||
iymek sızıqlı integrallar anıqlanadı hám tómendegishe belgilenedi: |
||||
|
f (x, y, z)dx, |
f (x, y, z)dy, |
f (x, y, z)dz |
|
|
|
|
|
|
|
AB |
AB |
|
AB |
P(x, y, z)dx + Q(x, y, z)dy + R(x, y, z)dz .
AB
Ekinshi túr iymek sızıqlı integraldıń bar bolıwı hám onı esaplaw.
Meyli AB iymek sızıq
x = x(t), |
( t ) |
(1) |
|
||
y = y(t) |
|
|
teńlemeler sistemasi menen anıqlanǵan bolıp, x = x(t) |
funkciya [ , ] úzliksiz, |
|||||
x (t) tuwındıǵa |
iye, |
y(t) |
funkciya |
[ , ] |
úzliksiz hám |
|
= ( x( ), y( )), B = ( x( ), y( )) bolsın. t parametr |
dan ǵa qarap ózgergende |
|||||
|
(x, y) = (x(t), y(t)) |
noqatı A dan B |
|
|
||
AB iymek sızıqtıń |
qarap AB nı sızamız. |
|||||
328
1-teorema. Eger f (x, y) |
funkciya |
|
|
|
|
|
|
AB da úzliksiz bolsa, onda ekinshi túr |
|||||||
iymek sızıqlı integral |
|
|
|
|
|
|
|
|
|
f (x, y)dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AB |
|
|
|
|
|
bar bolıp, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x, y)dx = f (x(t), y(t))x (t)dt |
(2) |
|||||
|
|
|
|
|
|
|
|
|
AB |
|
|
|
|
|
|
boladı. |
|
|
|
|
|
|
|
Meyli (1) sistemadaǵı |
x(t) , y(t) |
funkciyalar |
, |
úzliksiz bolıp, |
y(t) |
||
funkciya bolsa úzliksiz y'(t) tuwındıǵa iye bolsın. |
|
|
|
||||
|
|
|
|
|
|
|
|
2-teorema. Eger f (x, y) |
funkciya AB |
úzliksiz bolsa, onda ekinshi túr |
|||||
iymek sızıqlı integral |
|
|
|
|
|
|
|
|
|
f (x, y)dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AB |
|
|
|
|
|
bar bolıp, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4) |
f (x, y)dy = f (x(t), y(t))y (t)dt |
|
||||||
|
|
|
|
|
|
|
|
AB |
|
|
|
|
|
|
|
boladı. |
|
|
|
|
|
|
|
Meyli (1) sistemadaǵı |
x(t), y(t) |
funkciyalar |
, |
úzliksiz x'(t), |
y'(t) |
||
tuwındılarǵa iye bolsın. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3-teorema. Eger P(x, y) hám Q(x, y) funkciyalar AB |
úzliksiz bolsa, onda |
||||||
iymek sızıqlı integral
P(x, y)dx + Q(x, y)dy
AB
bar bolıp,
P(x, y)dx + Q(x,
AB
boladı.
Eger AB iymek sızıq menen berilgen bolsa, onda
|
|
|
|
|
(5) |
y)dy = [P(x(t), y(t))x (t) + Q(x(t), y(t))y (t)]dt |
||
|
|
|
y = y(x) , (a x b) , x = x( y) |
(c y d ) teńlemeler |
|
iymek sızıqlı integrallar ápiwayı kóriniske iye boladı.
329