
Matematikaliq analiz oqiw qollanba
.pdf
|
|
|
|
f (x, y, z)dxdxydz = V ( (x, y, z) V : m f (x, y, z) M ) |
|||||||||
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
boladı. |
|
|
|
|
|
|
|
|
|
|
|
||
|
Úsh eseli integrallardı esaplaw. Úsh eseli integrallardı esaplaw formulaları |
||||||||||||
integrallaw kópliktiń kórinisine qarap túrlishe boladı. |
|
|
|
|
|
||||||||
|
а) Meyli f (x, y, z) funkciya R3 |
keńisliktegi |
|
|
|
|
|
||||||
|
|
|
|
V = {( x, y, z) R3 : a x b, c y d , p z q} |
|
||||||||
kóplikte úzliksiz bolsın. Onda |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
b |
d |
q |
|
|
|
|
|
|
|
|
|
|
f (x, y, z)dxdydz = [ ( f (x, y, z) dz)dy]dx |
(2) |
|||||||
|
|
|
|
|
V |
a |
c |
p |
|
|
|
|
|
boladı. |
|
|
|
|
|
|
|
|
|
|
|
||
|
б) |
Meyli R3 |
keńisliktegi V |
kóplik |
– |
pásten |
z = |
1 |
(x, y) , |
joqarıdan |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z = |
2 |
(x, y) |
betlik, |
(bunda D R2 kóplik |
V denenıń |
|
X 0Y |
tegisliktegi |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
proekciyası) penen shegaralanǵan kóplik bolsın. Eger |
V da |
|
f (x, y, z) úzliksiz, |
||||||||||
1 (x, y) |
hám 2 (x, y) funkciyalar D da úzliksiz bolsa, onda |
|
|
|
|
||||||||
|
|
|
|
|
|
|
2 ( x, y ) |
|
|
|
|
||
|
|
|
|
|
|
|
|
f (x, y, z)dz |
|
|
(3) |
||
|
|
|
|
|
f (x, y, z)dxdydz = |
dxdy |
|||||||
|
|
|
|
|
V |
|
D |
1 ( x, y ) |
|
|
|
|
|
boladı.
в) Meyli б) daǵı D kóplik
|
|
D ={( x, y) R2 : a x b, (x) y |
2 |
(x)} |
||
|
|
|
|
1 |
|
|
bolıp, 1 |
hám 2 |
funkciyalar [a,b] да úzliksiz bolsın. Onda |
||||
|
|
b 2 ( x) 2 |
( x, y) |
|
|
|
|
f (x, y, z)dxdydz = [ |
( |
f (x, y, z) dz)dy]dx |
|||
|
V |
a 1 ( x) |
1 ( x, y) |
|
|
|
boladı.
1-mısal. J = (x + y + z)dxdydz integraldı esaplań, bunda
V
V= {( x, y, z) R3 : 0 x 1,0 y 3,0 z 2} .
◄Joqarıdaǵı (2) formuladan paydalanıp berilgen integraldı esaplaymız:
310

1 |
3 2 |
|
|
|
|
|
1 |
3 |
|
|
|
|
z |
2 |
|
z=2 |
1 3 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
[ ( (x + y + z)dz)dy]dx = [ (xz + yz + |
|
|
|
|
|
) dy]dx = [ 2(x + y +1)dy]dx = |
|||||||||||||||||||
|
|
2 |
|||||||||||||||||||||||
0 0 0 |
|
|
|
|
|
0 0 |
|
|
|
|
|
|
z=0 |
0 0 |
|||||||||||
|
1 |
|
|
|
y |
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
= 2(xy + |
|
+ y) yy==30 dx = (6x +15)dx =18 . ► |
||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
0 |
|
|
2 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
2-mısal. z 2 dxdydz |
|
|
integraldı |
|
|
|
|
esaplań, |
bunda V – tómendegi |
||||||||||||||
|
|
|
(V ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
z = |
|
x2 + y2 konus hám z = h tegislikler menen shegaralanǵan kóplik. |
|||||||||||||||||||||||
|
|
◄ V nıń XOY tegisliktegi proekciyası |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
D ={( x, y) R2 : x2 + y 2 h2 } |
|
|
|
|||||||||||||||||
boladı. (3) formuladan paydalansaq |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
h |
|
|
|
|
|
h |
3 |
|
|
|
1 |
|
3 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
J = |
z 2 dz dxdy = |
|
|
|
|
|
|
− |
|
|
|
(x2 + y |
2 )2 dxdy . |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
D |
|
3 |
|
|
|
3 |
|
|
|
|
|||||
|
|
|
2 |
+ y |
2 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
D |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Bul integralda
x = r cos ,
y = r sin
almastırıp, esaplasaq
J = |
2 h |
h3 |
− |
1 |
|
r |
3 |
|
|
d = |
1 |
h |
5 |
. ► |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
3 |
3 |
|
rdr |
|
5 |
|
|||||||
|
0 0 |
|
|
|
|
|
|
|
|
|
|
||||
|
17.4. Úsh eseli integrallarda ózgeriwshilerdi almastırıw |
||||
Meyli |
f (x, y, z) funkciya V R3 kóplikte berilgen hám úzliksiz bolsın. |
||||
Meyli |
|
|
|
|
|
|
x = (u, v, w), |
||||
|
|
||||
|
y = (u, v, w), |
||||
|
|
||||
|
z = (u, v, w) |
||||
sistema R3 kóplikti V kóplikke sáwlelendiredi. Onda |
|||||
f (x, y, z)dzdydz = f ( (u, v, w), (u, v, w), (u, v, w)) |
|
J |
|
dudvdw |
|
|
|
||||
V |
|
||||
311

boladı, bunda
|
|
dx |
|
dx |
|
dx |
|
|
|
|
|
|
|
|
|
du |
|
dv |
|
dw |
J = |
|
dy |
|
dy |
|
dy |
du |
|
dv |
|
dw |
||
|
|
|
|
|||
|
|
dz |
|
dz |
|
dz |
|
|
|
|
|
|
|
|
|
du |
|
dv |
|
dw |
boladı.
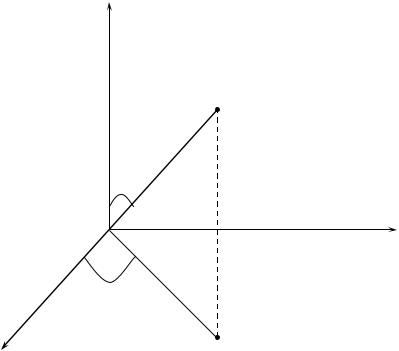
а) Dekart koordinataları x, y, z cilindrlik koordinatalar p, , z ǵa ótiw
|
x = p cos , |
|
y = p sin , |
|
z = z , |
(0 p + , 0 2 , |
− z + ) formulalar járdeminde ámelge |
asırıladı (45-sızılma). |
|
z
0
y
y
p
x
45-sızılma
Bul almastırıwdıń yakobian J = p bolıp,
f (x, y, z)dxdydz = f (p cos , |
p sin , z)pdpd dz |
|
V |
|
|
boladı.
312
z
p
0
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
46-sızılma |
|
||
|
б) Dekart koordinataları x, y, z sferalıq koordinatalar p, , ǵa ótiw |
|||||
|
|
x = p sin cos , |
||||
|
|
y = p sin sin , |
||||
|
|
|
z = p cos |
|
||
|
(0 p + , 0 2 , 0 ) formulalar arqalı ámelge asırıladı (46- |
|||||
sızılma) almastırıw yakobianı J = p 2 sin bolıp, |
||||||
f (x, y, z)dxdydz = f (p sin cos , p sin sin , p cos )p2 sin dpd d |
||||||
V |
V |
|
|
|
|
|
boladı. |
|
|
|
|
||
|
3-mısal. zdzdydz integraldı esaplań. Bunda V tómendegishe |
|||||
|
V |
|
|
|
|
|
|
|
x2 + y 2 |
= |
z 2 |
|
(h 0) |
|
|
r 2 |
h2 |
|||
|
|
|
|
|||
konustıń joqarı bólegi hám z = h tegislik penen shegaralanǵan kóplik.
◄Berilgen integralda ózgeriwshinı
x= p cos ,
y = p sin ,
313
|
|
|
|
|
z = z |
|
|
|
|
|
almastıramız |
|
|
|
|
|
|
|
|
|
|
|
x2 + y2 |
= |
z 2 |
|
p2 |
= |
z 2 |
z = |
h |
p , |
|
r 2 |
h2 |
r 2 |
h2 |
r |
|||||
|
|
|
|
|
|
|||||
(0 p r, 0 2 , 0 ).
Nátiyjede
|
r |
|
|
|
h |
|
|
|
2 |
||||
zdxdydz = |
|
pzdz |
||||
V |
0 |
|
0 |
|
h |
p |
|
|
|
|
|
|
|
|
|
|
r |
|
||
|
|
|
|
|
||
|
|
|
|
|
|
d dp |
||
|
|
|
|
||
|
||
|
||
boladı. Keyingi integraldı
r |
2 |
|
z 2 |
z=h |
|
|
r 2 h2 |
|
h2 |
|
|
|
|
|||||||||||
|
|
p |
|
|
|
|
d dp = |
|
|
|
|
|
− |
|
|
|
|
p2 |
pd |
|
dp = |
|||
|
|
|
|
|
|
|
2 |
|
||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
2r |
|
|
|
|
|||||||
0 |
0 |
|
|
|
z= |
h |
p |
0 |
0 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
h2 r 2 r |
|
|
|
|
|
|
|
|
p2 r |
h2 r 2 |
|
||||||||||
|
|
= |
|
|
2 |
|
(r 2 − p2 )pdp = h2 |
|
|
|
= |
|
|
. |
||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
r |
|
|
|
|
|
|
|
|
2 |
|
|
4 |
|
|
||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|||||||
Demek, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J = |
h2 r 2 |
. ► |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4-mısal. J = (x2 + y 2 |
+ z 2 )dxdydz integraldı esaplań, bunda V – |
|||||||||||||||||||||||
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 + y 2 + z 2 r 2 |
|
|
|
|
|
|
||||||||
shardan ibarat. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
◄ Bul integralda |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
x = psin cos , |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
y = p sin sin , |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
z = p cos |
|
|
|
|
|
|
|
|
||||||
almastırıp tabamız. Onda x2 |
+ y 2 + z 2 |
= p2 , |
J = p 2 sin bolıp, |
|||||||||||||||||||||
|
|
|
|
|
|
|
0 p r, 0 2 , 0 |
|
|
|||||||||||||||
boladı. Nátiyjede berilgen integral
314

J = (x2 |
r |
|
2 |
|
|
+ y 2 + z 2 )dxdydz = |
p2 p2 sin d d dp |
||||
V |
0 |
0 |
0 |
|
|
bolıp, bunnan
r |
|
2 |
|
|
r |
|
|
r |
4 r 5 |
||
p4 sin d d dp = (p4 sin 2 )d dp = 4 p4 dp = |
|
. |
|||||||||
5 |
|||||||||||
0 |
0 |
0 |
|
|
0 |
0 |
|
0 |
|
||
Demek, J = 4 r 5 . ►
5
17.5. Eseli integraldıń qollanıwları
Tegis figuranıń maydanı. Tegislikte maydanǵa iye bolǵan D figura berilgen bolsın. Bul figuranıń maydanı
D = dxdy |
(1) |
D
boladı.
Mısal. Tegisliktıń birinshi shereginde
x2 + y 2 = 2ax , y 2 = 2ax , x = 2a ( a 0`) sızıqlar menen shegaralanǵan figuranıń maydanın tabıń.
◄ Bul figura 42-sızılmada keltirilgen. x
D
0 |
a |
2a |
y |
42-sızılma
315

(1) formuladan figuranıń maydanı
D = dxdy
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D = (x, y) R2 |
|
|
|
|
|
|
|
|
|
. |
|
||||||||||||
bolıp, |
bunda |
|
: 0 x 2a, 2ax − x2 |
|
|
Integraldı |
||||||||||||||||||||||
|
y |
|
2ax |
|||||||||||||||||||||||||
esaplap |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2a |
|
2ax |
|
2a |
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
16 − 3 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
2 |
|
|
2 |
|
|||||
D = ( |
|
dy)dx = ( 2ax − |
|
2ax − x |
)dx = |
a |
− |
a |
= |
a |
. ► |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
3 |
|
|
|
|
2 |
|
|
6 |
|
|
|
|||
|
2ax−x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Denenıń kólemi. R3 |
keńislikte Dekart koordinatalar sistemasında jaylasqan |
||||||||||||||||||||||||||
V deneni qaraymız. Bul |
dene |
joqarıdan |
z = f (x, y) |
|
betlik, qaptal tárepten |
|||||||||||||||||||||||
jasawshıları Oz kósherine parallel cilindrlik betlik hám |
tómennen X 0Y |
|||||||||||||||||||||||||||
tegisliginde shegaralanǵan tuyıq |
D kóplik penen shegaralanǵan dene bolsın. |
|||||||||||||||||||||||||||
Bunda |
f (x, y) funkciyanı D da úzliksiz dep qaraymız. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
D kópliktıń P = D1, D2 ,..Dn bólekleniwin alayıq. Onda |
|
|
|
|
|
||||||||||||||||||||||
|
mk |
= inf f (x, y) : (x, y) Dk , M k |
= sup f (x, y) : (x, y) Dk |
|
|
|||||||||||||||||||||||
bar boladı boladı. Bunda |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
n |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A = mk Dk , B = M k Dk |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
k =1 |
|
|
|
k =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
qosındılar sáykes túrde V deneniń ishine jaylasqan |
A kópjaqlınıń kólemi, V |
|||||||||||||||||||||||||||
deneni óz ishine alǵan B kópjaqlınıń kólemi bolıp, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
A B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
boladı. D kóplikti túrli bólekleniwler nátiyjesinde payda bolǵan A hám B kópliklerdıń shegaralanǵanlıǵınan sup A , inf B lardıń bar bolıwınan kelip shıǵadı. f (x, y) funkciya tuyıq D kóplikte úzliksiz. Demek, ol D da teń ólshewli úzliksiz. Onda 0 alǵanda hám sonday 0 tabılıp, D kópliktnıń p bolǵan qálegen
P = D1 , D2 ,..Dn
bólekleniwi ushın hár bir Dk da ( k =1,2,3,...n ) funkciyanıń terbeliwi
M k − mk D
316
teńsizlikti qanaatlandıradı. Usılardı esarqa alıp
|
|
|
|
|
|
n |
|
|
|
|
|
n |
|
inf B −Sup A B − A = M k Dk |
− mk Dk = |
|
|||||||||||
= (M k − mk ) Dk |
|
k =1 |
|
|
|
|
|
k =1 |
|
||||
Dk = D = . |
|
||||||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
k =1 |
|
|
|
|
D |
|
D |
|
|
|
|
||
Demek, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 inf B −sup A . |
|
|
|
|
||||||||
Keyingi qatnastan |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
inf B = sup A |
|
|
|
|
||||||||
kelip shıǵadı. Bunnan V dene kólemge iye bolıp hám onıń kólemi V nıń |
|
||||||||||||
|
V = inf B = sup A |
|
|
|
(2) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
ekenligin bildiredi. Bunnan sup B = f (x, y)dxdy , inf A = f (x, y)dxdy |
|
||||||||||||
|
|
D |
|
|
|
|
|
|
|
|
D |
|
|
hám (2) teńlikke kóre |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
||
f (x, y)dxdy = f (x, y)dxdy = f (x, y)dxdy |
(3) |
||||||||||||
− |
|
D |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
D |
|
|||||
D |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
boladı. (2) hám (3) den |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V = f (x, y)dxdy |
|
|
|
(4) |
||||||||
|
D |
|
|
|
|
|
|
|
|
|
|||
kelip shıǵadı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
2-mısal. Keńislikte |
x 2 + y 2 + z − 4 = 0 |
betlik |
hám z = 0 tegislik penen |
||||||||||
shegaralanǵan denenıń kólemin tabıń. |
|
|
|
|
|
|
|
|
|
||||
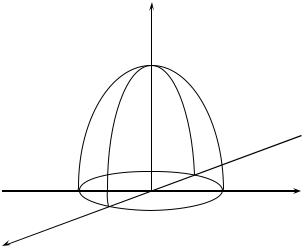
◄ Bul dene 43-sızılmada keltirilgen bolıp, D – XoY tegislikteǵi x2 + y 2 |
4 |
||||||||||||
dóńgelekten ibarat. |
|
|
|
|
|
|
|
|
|
|
|
|
|
317
z
4
−2 |
0 |
2 |
y |
x |
|
|
|
|
43-sızılma |
|
|
Betliktıń teńlemesin z = 4 − x 2 − y 2 |
kórniste |
jazıp, (4) formuladan |
|
paydalanıp |
|
|
|
V = (4 − x 2 |
− y 2 )dxdy , |
(5) |
|
|
D |
|
|
bunda
D= (x, y) R 2 : x2 + y 2 4 ,
(5)integralda ózgeriwshilerdi x = r cos , almastırıp esaplasaq
y = r sin
4 − x2 − y 2 = 4 − r 2 , J (r, ) = r , 0 r 2 , 0 2 ,
|
2 2 |
2 |
|
r |
4 |
|
|
(4 − x2 − y 2 )dxdy = ( (4 − r 2 )rdr)d = (2r 2 |
− |
|
|
)02 d = 8 |
|||
|
|
|
|||||
D |
0 0 |
0 |
4 |
|
|
||
Demek, denenıń kólemi V = 8 teń. |
|
|
|
|
|
|
|
Betliktıń maydanı. Meyli tegislikte |
maydanǵa iye |
|
bolǵan D |
||||
z = f (x, y) |
funkciya berilgen bolıp, ol usı kóplikte úzliksiz f x (x, y) , |
||||||
.
kóplikte f y (x, y)
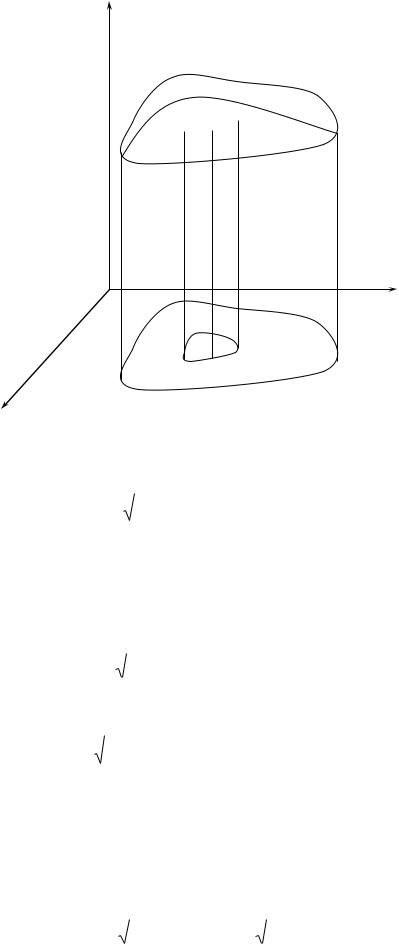
tuwındılarǵa iye bolsın. Bul funkciyanıń grafigi R3 keńislikte S betlik (44– sızılma) ańlatılǵan.
318
z
4
 S
S
0
y
x
44– sızılma
Bunday betliktıń maydan túsinigi hám onı eki eseli integral arqalı
|
|
|
|
S = |
1 + f x 2 (x, y)+ f y 2 (x, y)dxdy |
(6) |
|
(D ) |
|
|
|
tabıladı.
3-mısal. Tiykarınıń radiusı r , biyikligi h ǵa teń dóńgelek konustıń qaptal
betin tabıń. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
◄ Konus betlik |
z = |
|
|
|
x2 + y 2 |
|
|
teńleme menen ańlatıladı. (6) formulaǵa |
|||||||||||||
|
r |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
kóre konustıń qaptal beti |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
S = |
|
1 + (zx |
2 (x, y))2 |
+ (zy |
2 (x, y))2 dxdy |
||||||||||||||||
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
boladı, bunda |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D = {( x, y) R 2 : x2 + y 2 r 2 } . |
|
|||||||||||||||||||
Eger |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z = |
h |
|
|
|
x |
|
|
, z |
= |
h |
|
|
|
y |
, |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
x |
|
r |
|
x2 + y 2 |
|
|
y |
|
r |
|
x2 + y 2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
319
