Добавил:

aysultan Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Каракалпакский государственный университет им. Бердаха

Предмет:

Дискретная математика

Файл:

Matematikaliq analiz oqiw qollanba

.pdf

Скачиваний:

Добавлен:

10.08.2024

Размер:

7.89 Mб

Скачать

☆

<<< < Предыдущая 11 12 13 14 15 16 17 18 19 20 21 2223 / 3623 24 25 26 27 28 29 30 31 32 33 34 35 > Следующая >>>

f (x)= f (x0 )+	1	m	2 f	xi xk	(1)

	2 i,k =1 xi xk
boladı, bunda ekinshi tártipli dara tuwındılar
(x10 + x1 , x20	+ x2 ,...,			xm0 + xm )

(0 1) noqatta esaplanǵan hám

x1 = x1 − x10 , x2 = x2 − x20 ,..., xm = xm − xm0 .

Berilgen f (x) funkciyanıń ekinshi tártipli dara tuwındılarınıń stancionar noqattaǵı

x0 mánislerin

a = 2 f (x0 ) ( i ,k =1,2,...,m )

ik	xi xk

menen belgileymiz. Barlıq ekinshi tártipli dara tuwındılar

2 f

xi xk

larnıń x0 = (x10 , x20 ,..., xm0 ) noqatta úzliksizliginen aik = aki hám

2 f (x10 + x1 , x20 + x2 ,..., xm0 + xm )

2 f (x0 )

xi xk

kelip shıǵadı, bunda

xi →0

(i =1,2,...,m ) да

ik →0 .

Nátiyjede (1) teńlik

f (x0 )= f (x)− f (x

0 )

aik

xi xk + ik

xi xk

i,k =1

i,k

kóriniske keledi. Eger = x12

+ x22

+ ... + xm2

, xi = i , ( i =1, 2,..., m )

bolsa, onda xi →0 (i =1,2,...,m ) yaǵniy → 0 da

= 2 ( )

ik xk

xi = 2 ik i k

i,k =1

i,k

Esapqa alsaq, onda

f (x0 )=

ai,k i k

+ ( )

(2)

i,k =1

220

boladı. (2) teńlikten f (x0 ) nıń belgisi koefficentleri aik

2 f (x0 )

, (i, k = 1, 2,..., m)

x x

i k

aik i k

(3)

i,k =1

kvadratlıq formaǵa baylanıslı boladı.

2-teorema. Eger (3) kvadratlıq forma oń anıqlanǵan bolsa, onda f (x)

funkciyanıń

noqatta lokal minimumǵa, teris anıqlanǵan bolsa, onda lokal

maksimumǵa erisedi.

Eger (3) kvadratlıq forma anıq emes bolsa, bolsa

f (x)

funkciyanıń

noqatta lokal ekstremumǵa erispeydi.

Meyli

f (x, y)

funkciyanıń

(x , y

) R2

noqatnıń

bazı bir

((x , y

))

dógereginde ( 0) berilgen bolıp, mına shártler orınlı bolsın:

1) f (x, y)

funkciyanıń

U ((x0 , y0 ))

úzliksiz

hám

úzliksiz

f x' , f y'

f ''2 ,

f xy''

, f ''2

dara tuwındılarǵa iye,

2) (x , y

) stancionar noqat,

(x , y

)= 0,

f '

(x , y

)= 0 .

Bunnan

f (x0 , y0 )= f (x, y)− f (x0 , y0 )=

(a11 x2

+ 2 a12 x y + a22 y2

+ 11 x2

+ 2 12 x y + 22 y2 )

(*)

kelip shıǵadı, bunda

a = f ''2 (x

, y

), a = f ''

, y

)= f ''

, y

)

, a

= f ''

, y

)

y 2

bolıp,

x →0 , y →0 да 11 →0 , 12 →0 , 22 →0

boladı.

3-teorema. Eger

a	x2 + 2a	x y + a	22	y2	(4)
11	12		22

kvadratlıq forma oń anıqlanǵan, yaǵniy

221

a 0 ,	a11 a12	=a a	22	− a2	0
11	a21 a22	11	22	12
	a21 a22

bolsa, onda f (x, y) funkciyanıń (x0 , y0 ) noqatta lokal minimumǵa erisedi, eger (4) kvadratlıq forma teris anıqlanǵan, yaǵniy

						a 0,						a11 a12			=a a				22		− a2					0
							11					a21		a22		11			22				12
												a21		a22
bolsa, onda f (x, y) funkciya (x0 , y0 ) noqatta lokal maksimumǵa erisedi.
3-eskertiw. Eger a11 a22 − a122														0 bolsa, onda											f (x, y) funkciyanıń (x0 , y0 )
noqatta ekstremumǵa iye bolmaydı.
4-eskertiw. Eger a								a	22	− a2				= 0 bolsa, onda f											(x, y)		funkciyanıń (x , y						)
							11		22		12																					0	0
noqatta ekstremumǵa erisiwi múmkin, erispewide																						múmkin
Mısal.			f (x, y)= x2 + xy + y2 − 2x − 3y funkciyanı ekstremumǵa tekseriń.
◄Berilgen funkciyanıńnıń stancionar noqatların tabamız
		f ' (x, y)= 2x + y − 2,												2x + y − 2 = 0,												x =		1
		f ' (x, y)= 2x + y − 2,												2x + y − 2 = 0,												x =
			x																						0		3
																											3
		f y' (x, y)= x + 2 y − 3,												x + 2y − 3 = 0,												y =			4	.
		f y' (x, y)= x + 2 y − 3,												x + 2y − 3 = 0,												y =	3			.
																											3
1		4											''									''									''
Demek,	,		stancionar noqat. f										x	2 (x, y)= 2 ,						f xy			(x, y)=1 , f								y	2 (x, y)= 2 .
Demek,	,		stancionar noqat. f											2 (x, y)= 2 ,						f xy			(x, y)=1 , f									2 (x, y)= 2 .
3		3
3		3
Demek, a	= 2, a			= 1, a	22	= 2		, a			= 2 0 hám a									a		22	− a2 = 3 0 bolǵanlıǵı ushın
11			12		22				11									11				22			12
				1		,	4
berilgen funkciyanıń								noqatta lokal minimumǵa erisedi hám
berilgen funkciyanıń								noqatta lokal minimumǵa erisedi hám
				3			3
																1		4						7
								min f (x, y)= f									,				= −
								min f (x, y)= f									,				= −
																3 3								3

boladı.►

222

12-§. SANLÍ QATAR

12.1. Sanlı qatarlar túsinigi, onıń jıynaqlılıǵı hám taralıwshılılıǵı. Jıynaqlı qatarlardıń qásiyetleri

Meyli

{an }: a1 , a2 , a3 ,...,an ,...

haqıyqıy sanlar izbe-izligi berilgen bolsın. Olar járdeminde usı

a1 + a2 +a3 +... + an +...

(1)

ańlatpanı payda etemiz. (1) ańlatpa sanlı qatar, qısqasha qatar delinedi hám ol


an kórinisinde belgilenedi:
n=0

an = a1	+ a2	+ a3	+ ... + an + ...
n=1
Bunda a1 , a2 , a3 ,...,an ,... sanlar qatardıń aǵzaları, an bolsa qatardıń ulıwma
aǵza (yaki n -aǵzası) delinedi.
Tómendegi
Sn = a1 + a2 +... + an			(n =1,2,3,...)

qosındı (1) qatardıń n -dara qosındısı delinedi.

Demek, (1) qatar berilgende hár waqıtta bul qatardıń dara qosındılarınan ibarat usı Sn :

S1, S2 , S3,..., Sn ,...

izbe-izlikti payda etiw múmkin. Máselen,

1		+	1		+ ... +		1			+ ...

1 2			2 3				n(n +1)
qatardıń dara qosındısı
Sn =	1	+	1		+	1		+ ... +	1		=
	2			2 3					n(n +1)
1					3	4

223

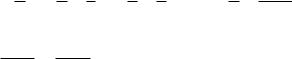
=(1− 12) + (12 − 13) + (13 − 14) +... + (1n − n 1+1) =

=1− n 1+1 = n n+1

bolıp, olardan dúzilgen		Sn izbe-izlik
	1	,	2	,	3	, ... ,	n	, ...
2			3		4		n +1

boladı.
1-anıqlama. Eger		n → da Sn izbe-izlik S							ke (S R ) jıynaqlı bolsa,

onda (1) qatar jıynaqlı, al S onıń qosındısı delinedi.


lim Sn = S , S = an .
n→	n=1

Eger Sn izbe-izlik shekli limitke iye bolmasa (limiti iye bolmasa yamasa sheksizlik bolsa), onda (1) qatar taralıwshı delinedi.

1-mısal.

+ ... +

+ ... qatar ushın

n=1 n(n −1) 1

n(n +1)

Sn =1−

bolıp, lim Sn = lim(1 −

) =1 boladı. Demek, berilgen qatar

+ n

n→

n +1

jıynaqlı hám onıń qosındısı 1 ge teń,

n=1

=1.

n(n −1)

2-mısal. n =1+ 2 + 3 +... + n

+... qatar taralıwshı boladı, sebebi

n=1

= 1 + 2 + 3 + ... + n =

n(n +1)

ushın

lim Sn

= + .

n→

3-mısal. (−1)n+1

= 1 −1

+1 −1 + ... + (−1)n+1 + ...qatar ushın

т=1

224

	n+1		0, eger n − jup san
S = 1 − 1 + 1 − 1 + ... + ( −1)
S = 1 − 1 + 1 − 1 + ... + ( −1)		=
n			1, eger n − taq san
			1, eger n − taq san

bolıp ol n → da limitke iye emes.
Demek, berilgen qatar taralıwshı boladı.
Jıynaqlı qatarlardıń qásiyetleri.
Meyli bazı bir

an = a1		+ a2	+... + an +...	(1)
n=1
qatar berilgen bolsın. Onda

an = am+1			+ am+2 + ...	(2)

n=m+1

qatar (bunda m −tayınlanǵan natural san) (1) qatardıń qaldıǵı delinedi.

1-qásiyet. Eger (1) qatar jıynaqlı bolsa, onda (2) qatar hám jıynaqlı boladı hám kerisinshe; (2) qatardıń jıynaqlı bolıwınan (1) qatardıń jıynaqlılıǵı kelip shıǵadı.


2-qásiyet. Eger an	qatar jıynaqlı bolıp, onıń qosındısı S	ga teń bolsa,
n=1

onda c an qatar ham jıynaqlı hám onıń qosındısı c S ge teń boladı, bunda c 0

n=1

turaqlı san.


3-qásiyet. Eger an			, bn	qatarlar jıynaqlı bolıp, olardıń qosındısı sáykes
		n=1	n=1

túrde S1	hám S2	ge teń bolsa, onda (an + bn )			qatarı jıynaqlı hám onıń qosındısı
				n=1
S1 + S2	ge teń boladı.

4-qásiyet. Eger an			qatar jıynaqlı bolsa, onda n → da an			nolge umtıladı,
		n=1
				lim an = 0 .
				n→

◄ Meyli		an qatar jıynaqlı bolıp,			onıń qosındısı S	qa teń bolsın.
		n=1

Anıqlamaǵa tiykarlanıp

225

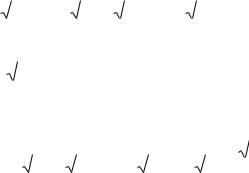
lim Sn

= lim(a1 + a2 + ... + an ) = S .

n→

Bunnan an = Sn − Sn−1 boladı. Keyingi teńlikten

lim an = lim(Sn − Sn−1 ) = S − S = 0 . ►

n→

Eskertiw. Qatardıń ulıwma aǵzası an nıń n → da nolge umtılıwnan onıń

jıynaqlı bolıwı hár waqıtta kelip shıqpaydı. Máselen, usı

= 1 +

+ ... +

+ ...

n=1

qatardıń ulıwma aǵzası an =

bolıp, ol n → da nolge umtıladı. Biraq bul

qatar taralıwshı, sebebi

Sn = 1 +

+ ... +

= n

İzbe-izlik n → da + ge umtıladı:

lim Sn = .

n→

Joqarıda keltirilgen 4)- qásiyet qatar jıynaqlı bolıwınıń zárúrli shártin

ańlatadı.

5-qásiyet. Meyli (1) qatar berilgen bolsın. Bul qatardıń aǵzaların tómendegi

(a1 + a2

+ ... + an

) + (an +1

+ an +2

+ ... + an

) + ...

(3)

qatardı payda etemiz, bunda

n1 n2 ...

bolıp, {nk } izbe-izlik natural sanlar izbe-izligi {n}

nıń dara izbe-izligi boladı.

Eger (1) qatar jıynaqlı bolıp, onıń qosındısı S ge teń bolsa, onda (3) qatar

hám jıynaqlı hám qosındısı S boladı.

Qatardıń jıynaqlılıǵı.

Teorema (Koshi teoreması). an

qatar jıynaqlı bolıwı ushın 0 san

n=1

alınǵanda hám sonday n0 N

tabılsa, n n0

hám m =1,2,3,... bolǵanda

Sn+m − Sn

an+1 + an+2 + .... + an+m

(4)

226

teńsizliktiń orınlanıwı zárúrli hám jetkilikli.


Eskertiw. Eger an qatar ushın (4) shárt orınlı bolmasa, onda		an qatar
n=1		n=1
taralıwshı boladı.
12.2. Oń aǵzalı qatarlar hám olardıń jıynaqlılıq belgileri
Meyli

an = a1	+ a2 +... + an +...	(1)
n=1
qatar berilgen bolsın. Eger bul qatarda an 0	( n N) bolsa, onda (1) oń aǵzalı

qatar delinedi. Oń aǵzalı qatarlarda, olardıń dara qosındılarınan ibarat Sn izbeizlik ósiwshi izbe-izlik boladı.

Haqıyqattan da,

Sn+1 = a1 + a2 +... + an + an+1 = Sn + an+1 Sn .


1-teorema. Oń aǵzalı an qatardıń jıynaqlı bolıwı ushın Sn
n=1
izbe-izliktiń joqarıdan shegaralanǵan bolıwı zárúrli hám jetkilikli.
◄ Zárúrligi. (1) qatar jıynaqlı bolsın. Onda n → da	Sn izbe-izlik
shekli limitke iye boladı. Jıynaqlı izbe-izliktiń qásiyetine	muwapıq Sn
shegaralanǵan, tiykarınan joqarıdan shegaralanǵan boladı.
Jetkilikligi. Sn izbe-izlik joqarıdan shegaralanǵan bolsın. Onda monoton
izbe-izliktiń limiti haqqındaǵı teoremaǵa muwapıq Sn izbe-izlik n → da

shekli limitke iye boladı. Demek, (1) qatar jıynaqlı boladı. ►


Eskertiw. Eger an oń aǵzalı qatarda, onıń dara qosındalarınan ibarat Sn
n=1
izbe-izlik joqarıdan shegaralanbaǵan bolsa, onda qatar taralıwshı boladı.
Oń aǵzalı qatarlarda salıstırıw teoremaları.

Meyli eki an hám	bn oń aǵzalı qatarlar berilgen bolsın.
n=1	n=1

227

2-teorema. Meyli an hám

bn qatarlar ushın n N da

n=1

an bn

(2)

teńsizlik orınlansın. Eger

1) bn

qatar jıynaqlı bolsa, onda an

qatar jıynaqlı boladı,

n=1

2) an

qatar taralıwshı bolsa, onda bn qatar taralıwshı boladı.

n=1

1-mısal. sin

qatardı jıynaqlılıqqa tekseriń.

n=1

◄ Bunnan, bul qatar aǵzaları ushın

0 sin

(n =1,2,3,...)

teńsizlik orınlı boladı.

Nátiyjede

berilgen qatardıń

har bir

aǵzası jıynaqlı

qatardıń

n=1

(geometriyalıq qatardıń) sáykes aǵzasınan kishi boladı. 2-teoremaǵa muwapıq berilgen qatar jıynaqlı boladı. ►


3-teorema. Meyli oń aǵzalı an			hám bn	qatarlardıń ulıwma aǵzaları
		n=1	n=1
ushın
lim	an	= K	(b 0,	n =1,2,...)
lim		= K	(b 0,	n =1,2,...)
n→ b			n
	n
bolsın. Bunda:

1) K + bolıp, bn qatar jıynaqlı bolsa, onda an					qatar hám jıynaqlı
n=1				n=1
boladı.

2) K 0 bolıp, bn qatar taralıwshı bolsa, onda an					qatar taralıwshı
n=1				n=1

boladı.

228

Saldar. Oń aǵzalı an hám

qatarlar ushın

n=1

lim

= K

(0 K + )

n→ b

bolsa, onda

hám

qatarlar bir waqıtta jıynaqlı yamasa taralıwshı

n=1

boladı.

2-mısal.

qatar jıynaqlılıqqa tekseriń.

n=1 n1+

◄

Berilgen

qatar

menen

birge

taralıwshılıǵı

málim bolǵan

n=1 n

garmonikalıń qatardı qaraymız. Bul qatarlardıń ulıwma aǵzaları ushın

lim

n1+

= lim

= 1

n→ n n

n→

boladı. Demek, berilgen qatar taralıwshı boladı. ►

4-teorema. Meyli oń aǵzalı an hám bn qatarlar ushın

n=1

an+1

bn+1

bolsın (an

0, bn

n =1,2,3,...)

Bunda:

1) bn

qatar jıynaqlı bolsa, onda an

qatar jıynaqlı boladı,

n=1

2) an

qatar taralıwshı bolsa, onda bn

qatar taralıwshı boladı.

n=1

Joqarıda keltirilgen teorema hám mısallardan kórinip turǵanday, oń aǵzalı qatardıń jıynaqlılıǵı yamasa taralıwshılıǵın bilgen jaǵdayda, aǵzaları bul qatar

229

<<< < Предыдущая 11 12 13 14 15 16 17 18 19 20 21 2223 / 3623 24 25 26 27 28 29 30 31 32 33 34 35 > Следующая >>>

Соседние файлы в предмете Дискретная математика

#
10.08.20242.46 Mб6Aniq integrallar.pdf
#
09.08.20243.06 Mб5Apiwayi differencialliq tenlemeler.pdf
#
09.08.20243 Mб7Differencialliq tenlemeler.pdf
#
09.08.20241.38 Mб17Joqari matematika paninen lekciyalar.pdf
#
09.08.20241.17 Mб11Matematika (Lekciya).pdf
#
10.08.20247.89 Mб15Matematikaliq analiz oqiw qollanba.pdf
#
10.08.20244.64 Mб17Matematikaliq analiz.pdf
#
10.08.20246.32 Mб73Matematikani oqitiw metodikasi.pdf
#
10.08.20241.7 Mб4Tenlemeler ham tensizlikler.pdf
#
10.08.20241.65 Mб3Tensizliklerdi dalillew usillari.pdf