Добавил:

aysultan Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Каракалпакский государственный университет им. Бердаха

Предмет:

Дискретная математика

Файл:

Matematikaliq analiz oqiw qollanba

.pdf

Скачиваний:

Добавлен:

10.08.2024

Размер:

7.89 Mб

Скачать

☆

<<< < Предыдущая 10 11 12 13 14 15 16 17 18 19 20 2122 / 3622 23 24 25 26 27 28 29 30 31 32 33 34 > Следующая >>>

kóriniske keledi. Demek, f (x0 )= df (x0 )+ 0( ). Eger → 0 da f (x0 ) df (x0 ) kelip shıǵadı.

Quramalı funkciyanıń differencialı. Differencial formanıń invariantlıǵı.

Meyli

x1 = 1 (t )= 1 (t1 ,t2 , ,tk ), x2 = 2 (t )= 1 (t1 ,t2 , ,tk ),

xm = m (t )= 1 (t1 ,t2 , ,tk ) funkciyalarınıń hár biri M Rk kóplikte berilgen bolıp,

E = (x1 , x2 , , xm ) Rm : x1 = 1 (t)= 1 (t1 ,t2 , ,tk ),

x2 = 2 (t)= 1(t1 , t2 , , tk ), , xm = m (t)= 1(t1 , t2 , , tk ) kóplikte bolsa f (x1, x2 ,..., xm ) funkciya anıqlanǵan bolsın. Bular járdeminde

f (x (t )) = f (x1 (t ), x2 (t ),..., xm (t )) = F (t1,t2 ,...,tk )

quramalı funkciya payda qılınǵan bolsın.

Meyli xi = i (t1 , ,tk )

funkciyalar (i =1,2, m)

t 0 = (t10 , ,tk0 ) noqatta

differenciallanıwshı

bolıp,

f (x)= f (x1 , x2 , , xm )

funkciya

sáykes

x0 = (x10 , x20 , , xm0 )

noqatta

(x10 = 1 (t 0 ), x20 = 2 (t 0 ), , xm0

= m (t 0 ))

differenciallanıwshı

bolsa,

quramalı

funkciya

t 0 = (t10 , ,tk0 )

noqatta

differenciallanıwshı boladı. Bunda f (x(t)) funkciya

t1 ,t2 , ,tk ózgeriwshilerge

baylanıslı eken, onda

df =

dt +

+ +

(3)

boladı. Demek, quramalı funkciyanıń differencialı

df =

dx +

dx +... +

(4)

boladı.

Biz joqarıda f (x) hám f (x(t)) quramalı funkciyanıń differencialı ushın (2) hám (4) ańlatpalardı taptıq. Bul ańlatpalardı salıstırıp olardıń forması birdey, yaǵnıy (2) hám (4) formulalarda funkciyanıń differencialı dara tuwındılarǵa sáykes

210

differenciallarǵa kóbeymelerinen dúzilgen qosındıǵa teń ekenligin kóremiz. Bul

qáseyt differencial formanıń invariantlıǵı delinedi.

Meyli

u = u (x1, x2 ,..., xm ) ,

v = v (x1, x2 ,..., xm ) funkciyaları E Rm

kóplikte

berilgen bolıp, x

= (x1 , x2 ,..., xm ) E noqatta differenciallanıwshı bolsın. Onda

1) d (u + v) = du + dv,

2) d (u v) = vdu + udv,

vdu − udv

3) d

, (v 0)

boladı.

Meyli u = f

(

)

funkciyanıń differencialı usı iymek sızıqqa (x , f

(

x )

noqatta

)

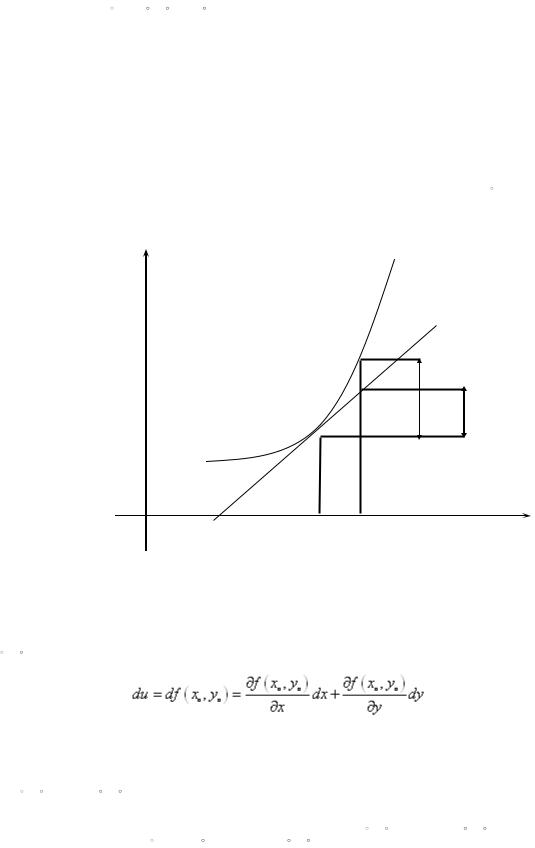
ótkizilgen urınbanıń ordinatasınıń ósimin ańlatadı (27-sızılma).

f (x)

(x0 , f (x0 )) f df

0	x0 x0 + x	x
	27-sızılma
Eki ózgeriwshili u = f (x, y)	((x, y) R2 ,u R) funkciyaǵa iye bolıp, onıń

(x , y ) noqattaǵı differencial

						(5)
boladı, bunda dx = x , dy = y .	x hám	y	lar jeterli kishi bolǵanда
f (x , y ) df (x , y ) yaǵnıy
f (x + x, y + y) f (x , y )+		f (x , y )		x +	f (x , y )	y
f (x + x, y + y) f (x , y )+				x +		y
		x1			y

211

juwıq formula payda boladı.

1-mısal. u = x y funkciyanıń differencialı tabıń.

◄ ux = yx y−1, uy = x y ln x. Onda (5) formulaǵa kóre du = yx y−1dx + x y ln xdy boladı.►

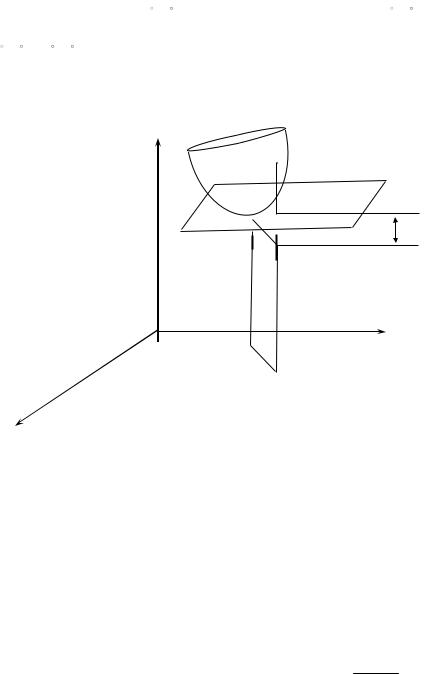
Endi z = f (x, y) funkciya differencialınıń geometriyalıq mánisin keltiremiz. z = f (x, y) funkciyanıń (x , y ) noqattaǵı differencialı df (x , y ) bul funkciya grafigine (x , y f (x , y )) noqattındaǵı urınbanıń tegisliktegi aplikatasınıń ósimin

ańlatadı eken (28-sızılma)

df (x0 , y0 )

0	(x0	, y0 )	y

28-sızılma

11.4. Kóp ózgeriwshili funkciyanıń joqarı tártipli tuwındı hám differencialları. Orta mánis haqqında teorema

Joqarı tártipli dara tuwındılar. Meyli f (x)= f (x1, x2 ,...., xm ) funkciya ashıq

E R m kópliktıń hár bir x =(x1, x2 ,...., xm ) E noqattında f x(ix) = fx'i ,(i =1, 2,...., m ) dara tuwındılarǵa iye bolsın. Bul dara tuwındılar x1 , x2 ,....., xm ózgeriwshilerdıń funkciyası bolıp, olar da dara tuwındılarǵa iye bolıwı mumkin:

212

(

)

( fx'i

(x))x

, ( i , k =1, 2 ,...., m ).

Bul dara tuwındılar berilgen

f (x)

funkciyanıń

ekinshi

tártipli dara

tuwındıları delinedi hám

(

)

yamasa fx x

(x),(i, k =1, 2,...., m )

xk xi

i k

f (x)

arqalı belgilenedi

(x)= x

= f xi

Eger i k

bolsa, onda

(x)

ekinshi tártipli dara tuwındı aralas tuwındı

delinedi. Eger i = k bolsa, ekinshi tártipli dara tuwındılar

2 f

(x)

= f x x (x)

xk xi

i k

tómendegishe

2 f (x)

= f

''2 (x) jazıladı.

f (x) funkciyanıń úshinshi, tórtinshi hám t.b. tártiptegi dara tuwındıları

joqarıdaǵıǵa

uqsas

anıqlanadı. Ulıwma

f (x)= f (x1, x2 ,..., xm )

funkciyanıń

xi , xi ,

....., xi

, xi

ózgeriwshileri

boyınsha

n -tártipli

dara

tuwındısı berilgen

n−1

funkciyanıń (n −1) – tártipli dara tuwındısı

n−1 f (x)

(i1

+ i2 + .... + in−1 = n −1)

.... x

n −1

n −2

nıń xi

ózgeriwshi boyınsha dara tuwındısı sıpatında anıqlanadı

n f

(

)

n−1 f

(

)

.... x x

.... x

in−1

Eger i1 ,i2 ,....,in

ler bir-birine teń bolmaǵanda

n f

.... xi

aralas

tuwındı

delinedi. Eger

i1 = i2 =... =in = k

bolsa, onda n – tártipli dara

tuwındılar tómendegishe

f (x)

jazıladı.

xkn

213

2 f	,	2 f	(i k )
x x	,	x x	(i k )
k i		i k

aralas tuwındılar funkciyanıń hár qıylı ózgeriwshilerı boyınsha differenciallaw tártibi menen parq qıladı

2 f

xi xk

f (x1 , x2 ,...., xm ) funkciyanıń dáslep xi ózgeriwshisi boyınsha, soń xk

ózgeriwshisi boyınsha dara tuwındısı esaplanǵan bolsa, al

2 f

xk xi

bolsa dáslep xk ózgeriwshisi boyınsha, soń xi ózgeriwshisi boyınsha dara tuwındısı esaplanadı. Olar bir-birine teń bolıwı mumkin, teń bolmawıda mumkin.

1-teorema. Meyli	f (x1 , x2 ,...., xm )	funkciya	x0 = (x10 , x20 ,..., xm0 ) E Rm
noqatta n márte differenciallanıwshı bolsın. Onda			x0 noqatta f (x , x ,...., x	m	)
			1 2
funkciyanıń qálegen n -tártipli aralas		tuwındılarınıń mánisi x1, x2 ,...., xm
ózgeriwshiler boyınsha qanday tártipde differenciallawǵa baylanıslı bolmaydı.
Joqarı tártipli differencialаr. Meyli		f (x)= f (x1, x2 ,...., xm ) funkciya ashıq
E R m kóplikte berilgen, x E noqatta eki márte differenciallanıwshı bolsın.
1-anıqlama. f (x)	funkciya differencialı d f (x) nıń differencialı berilgen

funkciyanıń x noqattaǵı ekinshi tártipli differencialı delinedi hám d 2 f (x) arqalı belgilenedi d 2 f (x)= d (d f (x)).

Ekinshi tártipli differencialı tómendegishe boladı

2									2
d			d x1 +			d x2 + ... +				f .

	f (x)=	x		x			x		d xm
		x		x	2		x	m
		1			2			m

f (x) funkciyanıń x noqattaǵı úshinshi, tórtinshi hám t.b. tártiptegi differencialları joqarıdaǵıday anıqlanadı.

Eger f (x) funkciya x noqatta n márte differenciallanıwshı bolsa, onda

214

n							n		(2)

			d x1 + x		d x2 + ... + x
d	f (x)=	x	d x1 + x	2	d x2 + ... + x			f
		1		2		m

boladı.

Quramalı funkciyanıń joqarı tártipli differencialları.


Meyli	f (x)= f (x1, x2 ,..., xm )	funkciyada x1, x2		,..., xm ózgeriwshilerdıń hár
biri t1,t2 ,...,tk	ózgeriwshilerdıń funkciyaları bolsın (xi			= i (t1,t2 ,...,tk )).
Qaralıp atırǵan f (x) hám xi		= i (t)	(i =1, 2,...., m) funkciyaler n márte

differenciallanıwshılıq shártlerin orınlanǵan deb, quramalı f (x(t)) funkciyanıń

joqarı tártipli differencialların esaplaymız.

Differencial formanıń invariantlıǵı qáseytine muapıq, quramalı funkciyanıń differencialı

d f =

d x

+.... +

d x

boladı. Differenciallaw qaǵıydalarınan paydalanamız hám funkciyanıń ekinshi tártipli differencialı

d 2 f =

dx +

+ .... +

f +

(3)

2 x +

d 2 x

+ .... +

d 2 x

Usı jol menen berilgen quramalı funkciyanıń keyinǵı tártiptegi

differencialları tabıladı.

1-eskertiw. (1) hám (3) formulalardı salıstırıp, ekinshi tártipli

differenciallardı

differencial

formanıń

invariantlıǵı

qáseyti orınlı emesligin

kóremiz.

2-eskertiw. Eger f (x1, x2 ,..., xm ) funkciya argumentlerı x1, x2 ,..., xm hár biri t1,t2 ,...,tk ózgeriwshilerinıń sızıqlı funkciyası bolsa, onda f (x) funkciyanıń ekinshi tártipli differencialı differenciallıq formanıń invariantlıq qáseytine iye boladı.

Orta mánis haqqında teorema.

215

Meyli f (x) = f (x1, x2 ,..., xm ) funkciya E R m kóplikte berilgen bolsın.

Bul E kóplikte sonday a = (a1, a2 ,..., am ), b = (b1, b2 ,...,bm ) noqatların qaraymız, bul noqatlardı birlesturıwshı tuwrı sızıq kesim E kóplikke tiyisli bolsın. Bul kesim

K = (x1, x2 ,..., xm ) Rm : x1 = a1 + t(b1 − a1 ), x2 = a2 + t(b2 − a2 ),..., xm = am + t(bm − am )

,(0 t 1)

noqatlar kópligi menen ańlatıladı K E .

1-teorema. Eger f (x) funkciya K kesimnıń a hám b noqatlarda úzliksiz bolıp, kesimnıń qalǵan barlıq noqatlarında differenciallanıwshı bolsa, onda K kesimde sonday c = (c1,c2 ,...,cm ) noqat tabılıp,

f (b)− f (a)= f x'1 (c)(b1 − a1 )+ f x'2 (c)(b2 − a2 )+.... + f x'm (c)(bm − am ) (1)

boladı.

Bul (1) formula Lagranjdıń shekli ósimler formulası delinedi.

Kóp ózgeriwshili funkciyanıń Тейлор formulası

Meyli

f (x)= f (x , x ,..., x

)

funkciya

ashıq

E R m kóplikte

berilgen

bolıp, U (x0 ) E bolsın, bunda x0

= (x10 , x20 ,..., xm0 ) hám 0 . x U (x0 )

hám

x 0 noqatlardı birlestiriwshi tuwrı sızıq kesimi

A = x10 + t(x1 − x10 ), x20 + t (x2 − x20 ),..., xm0

+ t(xm − xm0 ); 0 t 1

usı U (x0 ) ǵa tiyisli boladı.

f (x1, x2 ,...., xm )

funkciya U (x0 ) kóplikte (n +1)

márte differenciallanıwshı bolsın. Bul funkciyanı

A kóplikte qarasaq, 0,1

segmentte anıqlanǵan mına

F (t)= f (x10 + t(x1 − x10 ), x20 + t (x2 − x20 ),..., xm0 + t (xm − xm0 ))

Funkciyaǵa iye bolamız. F (t)

funkciya 0,1 da tuwındıǵa iye bolıp,

F ' (t )=

(x1

− x10 )+

(x2 − x20 )+ ... +

(xm − xm0 )=

(x1

− x1

(x2

− x2 )+ ... +

(xm − xm ) f

216

boladı, bunda f (x) funkciyanıń barlıq dara tuwındıları

(x10 + t(x1 − x10 ),

x20 + t(x2 − x20 ),..., xm0

+ t(xm − xm0 ))

(4)

noqatta esaplanadı. F (t )

funkciya k -tártipli (k =1,2,...,n +1) tuwındılarǵa iye

hám ol

(k )

0 k

(x1 − x1 )+

(x2 − x2 )+ ... +

(t)=

(xm − xm )

ǵa teń, barlıq dara tuwındılar (4) noqatta esaplanadı.

Solay etip, F (t ) funkciya

(n+1)

(t) tuwındılarǵa iye boladı.

(t), F (t),..., F

Teylor formulasına kóre t0

noqatta (0 t0 1)

F (t )= F (t0 )+ F ' (t0 )(t − t0 )+

F (t0 )(t − t0 )2 + ... +

(5)

F (n) (t0 )(t − t0 )n +

F (n+1) (c) (t − t0 )n+1

(n +1)!

boladı, bunda c = t0 + (t − t0 ),

F (1)= F (0)+ 1!1 F ' (0)+

kelip shıǵadı. Bunnan

0 1. Bul

2!1 F (0)+ ... +

F (0)= f

F (1)= f

teńlikte t0 = 0, t =1 bolsa, onda

1	F (n) (0)+	1	F (n+1) ( )
n!		(n +1)!

(x10 , x20 ,..., xm0 ),		(6)
(x1 , x2 ,..., xm )	,

(k )

(x1

− x1 )+

(x2 − x2 )+ ... +

(0)=

(xm − xm ) f

bolıwın esapqa alsaq, onda (5) hám (6) teńliklerden

f (x1 , x2 ,..., xm )= f (x10 , x20 ,..., xm0 )+

n 1

0 0

(x1 − x1

(x2 − x2 )+ ... +

f (x1 , x2 ,..., xm )+

(xm − xm )

k =1 k!

n+1

(x1−x10 )

(x2 − x20 )+

... +

(xm

− xm0 )

(n +1)!

f (x10

+ (x1 − x10 ), x20 + (x2 − x20 ), ...,

xm0 +

(xm − xm0

))

217

(0 1 ) teńlikke kelemiz. Bul kóp ózgeriwshili f (x1, x2 ,..., xm ) funkciyanıń Lagranj kórinistegi qaldıq Teylor formulası delinedi.

11.5. Kóp ózgeriwshili funkciyanıń ekstremum mánisleri. Ekstremumnıń zárúrli hám jetkilikli shártleri

Funkciyanıń ekstremumı. Zárúrli shárt. Meyli f (x)= f (x1, x2 ,..., xm ) funkciyanıń E R m kóplikte berilgen bolıp, x0 =(x10 , x20 ,..., xm0 ) E bolsın.

1-anıqlama. Eger sonday 0 san tabılıp, U (x0 ) E bolıp, x U (x0 ) da f (x) f (x0 ) bolsa, onda f (x) funkciyanıń x0 noqatta lokal maksimumǵa,

f (x) f (x0 ) bolsa, onda		f (x) funkciyanıń x0 noqatta lokal minimumǵa erisedi
delinedi.
2-anıqlama.	Eger	sonday	0 san	tabılıp, U (x0 ) E	bolıp,
x U (x0 )\ x0	da f (x) f (x0 )		bolsa, onda	f (x) funkciyanıń x0	noqatta
qatań lokal maksimumǵa, f (x) f (x0 ) bolsa, onda f (x) funkciyanıń x0					noqatta

lokal qatań minimumǵa erisedi delinedi.

Funkciyanıń lokal maksimum, lokal minimum ulıwma at penen lokal ekstremum delinedi. Bunda x0 noqat f (x) funkciyanıń lokal ekstremum noqatı, f (x0 ) ǵa bolsa funkciyanıń lokal ekstremum mánisi delinedi.

Funkciyanıń maksimum (minimum) mánisi tómendegishe belgilenedi:

f (x	0	)= max	f (x)
f (x		)= max	f (x)	f
		x U (x0 )

(x0 )= min	f (x) .
x U (x0 )

Meyli f (x0 )= f (x)− f (x0 ) ayırma f (x) funkciyanıń x0 noqattaǵı tolıq

ósimi delinedi.	f (x) funkciyanıń x0	noqatta lokal maksimumǵa erisse, onda
x U (x0 ) da	f (x0 ) 0 boladı hám kerisinshe. Eger f (x) funkciyanıń x0
noqatta lokal minimumǵa erisse, onda		x U (x0 ) da f (x0 ) 0 boladı hám

kerisinshe.

218

f (x)

1-teorema. Eger f (x)= f (x1, x2 ,...., xm ) funkciyanıń x0 = (x10 , x20 ,..., xm0 ) noqatta lokal ekstremumǵa erisse hám usı noqatta barlıq dara tuwındılarǵa iye bolsa, onda

f (x0 ) =0,(i =1, 2,..., m)

boladı.

1-eskertiw. Eger f (x) funkciyanıń bazı bir x0 noqatta lokal ekstremumǵa erisse hám usı noqatta differenciallanıwshı bolsa, onda

d f (x0 )= 0

boladı.

2-eskertiw. f (x)= f (x1, x2 ,..., xm ) funkciyanıń bazı bir x0 noqatta barlıq dara tuwındılarǵa iye hám

f (x0 ) = 0,( i = 1, 2,..., m )

bolıwınan berilgen funkciyanıń usı noqatta lokal ekstremumǵa erisiwi hár dayım kelip shıǵabermeydi.

Demek, 1-teorema funkciyanıń lokal ekstremumǵa erisiwinıń zárúrli shártin ańlatadı.

funkciyanıń dara tuwındıların nolge aylandıratuǵın noqatlar onıń

stancionar noqatları delinedi.
Funkciyanıń ekstremumǵa erisiwinıń jetkilikli shárti.
Meyli f (x) = f (x1, x2 ,..., xm ) funkciyanıń x0 Rm noqatınıń bazı bir	U (x0 )

dógereginde berilgen, usı dógerekte barlıq ekinshi tártipli úzliksiz dara tuwındılarǵa iye hám

f (x0 )= 0	(i =1, 2,...,m )
xi
bolsın. Bul funkciyanıńnıń Teylor	formulası	f (x0 )	= 0 shártti esapqa alǵan,

		xi

tómendegishe

219

<<< < Предыдущая 10 11 12 13 14 15 16 17 18 19 20 2122 / 3622 23 24 25 26 27 28 29 30 31 32 33 34 > Следующая >>>

Соседние файлы в предмете Дискретная математика

#
10.08.20242.46 Mб6Aniq integrallar.pdf
#
09.08.20243.06 Mб5Apiwayi differencialliq tenlemeler.pdf
#
09.08.20243 Mб7Differencialliq tenlemeler.pdf
#
09.08.20241.38 Mб17Joqari matematika paninen lekciyalar.pdf
#
09.08.20241.17 Mб11Matematika (Lekciya).pdf
#
10.08.20247.89 Mб15Matematikaliq analiz oqiw qollanba.pdf
#
10.08.20244.64 Mб17Matematikaliq analiz.pdf
#
10.08.20246.32 Mб73Matematikani oqitiw metodikasi.pdf
#
10.08.20241.7 Mб4Tenlemeler ham tensizlikler.pdf
#
10.08.20241.65 Mб3Tensizliklerdi dalillew usillari.pdf