
Matematikaliq analiz oqiw qollanba
.pdfkóp ózgeriwshili funkciyanıń dara tuwındıların tabıwda málim bolǵan tablitsa hám qaǵiydalardan paydalanıw mumkin. Eger f (x) = f (x1 , x2 ,..., xm ), g (x) = g (x1, x2 ,..., xm )
funkciyalar |
E Rm kóplikte berilgen bolıp, x E noqatta dara tuwındılarǵa iye |
|||||||||||||||||||||||
bolsa, onda |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1) c R: |
|
|
(c f (x))=c f (x) ; |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
xk |
|
|
|
|
xk |
|
|
|
|
|
|
|
|
2) (f (x)+ g (x))= f (x)+ g (x) ; |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
xk |
|
|
|
xk |
|
xk |
|
|
|
|
|
|
|||||||
|
3) (f (x) g (x)) |
|
f (x) |
g (x)+ f (x) |
g (x) |
|
|
|
||||||||||||||||
|
|
|
|
|
xk |
|
|
= xk |
|
|
xk |
; |
|
|
||||||||||
|
|
|
|
f (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
g (x) |
|
|
−2 |
|
f (x) |
|
|
|
|
g (x) |
|
|
|||||||||
|
4) |
|
|
|
|
|
|
|
= g (x) |
|
|
|
|
g (x)− f |
(x) |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
xk |
|
|
|
xk |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xk |
|
|
|||||||
|
|
|
|
(g (x) 0 ), |
k =1,2,...,m |
|
|
|
|
|
|
|
||||||||||||
|
boladı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Kóp ózgeriwshili funkciyanıń differenciallanıwshılıǵı. |
|
|
|||||||||||||||||||||
|
Meyli f (x)= f (x , x ,..., x |
m |
) |
funkciya E Rm kóplikte berilgen |
bolıp, |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
x0 =(x10 , x20 ,..., xm0 ) E, |
(x10 + x1 , x20 |
+ x2 ,..., xm0 |
+ xm ) E |
bolsın. Маълумки, |
||||||||||||||||||||
berilgen funkciyanıń x0 |
noqattaǵı tolıq ósimi |
|
|
|
|
|||||||||||||||||||
|
f (x0 )= f (x0 + x1 , x20 |
+ x2 ,..., xm0 + xm )− f (x10 , x20 ,..., xm0 ) |
|
|||||||||||||||||||||
bolıp, ol x1, x2 ,..., xm larǵa baylanıslı boladı. |
|
|
|
|||||||||||||||||||||
|
2-anıqlama. Eger x1, x2 ,..., xm ósimlerge baylanıslı bolmaǵan sonday |
|||||||||||||||||||||||
A , A ,...., A |
|
sanları tabılıp, funkciyanıń x0 |
noqattaǵı tolıq ósimi |
|
||||||||||||||||||||
1 2 |
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x0 )= A1 x1 + A2 x2 +.... + Am xm + 1 x1 |
+ 2 x2 +... + m xm |
(1) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kóriniste ańlatılsa, |
f (x) funkciya x0 |
noqatta differenciallanıwshı delinedi, bunda |
||||||||||||||||||||||
1 , 2 ,..., m |
|
|
|
|
lar |
|
|
|
x1 , x2 , , xm |
|
larǵa |
baylanıslı |
hám |
|||||||||||
x1 →0, x2 → 0,..., |
xm → 0 da sheksiz kishi shamalar. |
|
|
|||||||||||||||||||||
200
|
Eger (x10 , x20 ,..., xm0 ) |
hám |
(x10 + x1 , x20 + x2 ,..., xm0 |
+ xm ) |
noqatlar |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
arasındaǵı aralıq |
= |
|
x2 |
+ x2 |
+...+ x2 |
ushın, |
x →0, |
x |
→ 0,..., x → 0 |
|||||||||
|
|
|
|
|
1 |
|
2 |
|
|
m |
|
|
|
1 |
2 |
|
m |
|
da 1 x1 + 2 x2 +...+ m xm =0( ) bolıwın esapqa alsaq, (1) qatnas |
|
|||||||||||||||||
|
|
|
|
f (x0 )= A1 x1 + A2 x2 +....+ Am xm + 0( ) |
(2) |
|||||||||||||
kóriniske keledi. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Ádette (1) hám (2) qatnaslar |
|
f (x) |
|
funkciyanıń |
x0 |
noqatta |
|||||||||||
differenciallanıwshılıq shárti delinedi. |
|
|
|
|
|
|
|
|
|
|||||||||
|
1-mısal. |
|
|
f (x)= f (x1 , x2 ,..., xm )=x12 + x22 +...+ xm2 |
|
funkciyanıń |
||||||||||||
(x10 , x20 ,..., xm0 ) Rm noqatta differenciallanıwshı bolıwı kórsetiń. |
|
|
||||||||||||||||
|
◄Berilgen funkciyanıń x0 = (x10 , x20 ,..., xm0 ) |
noqattaǵı tolıq ósimin tabamız |
||||||||||||||||
|
f (x0 )=(x10 |
+ x1 )2 +(x20 |
+ x2 )2 +... +(xm0 + xm )2 − |
|
|
|
|
|
||||||||||
|
−(x102 |
+ x202 |
+... + xm02 )=2 x10 x1 + 2 x20 x2 +... + 2 xm0 |
xm + x12 + x22 +... + xm2 . |
||||||||||||||
Eger |
A =2 x0 , A =2 x0 ,..., A =2 x0 |
, = x , |
|
= x ,..., |
|
= x |
|
|
|
|||||||||
1 |
1 |
2 |
2 |
|
m |
m |
1 |
1 |
2 |
|
2 |
|
m |
m bolsa, onda |
|
|||
|
f (x0 )= A1 x1 + A2 x2 +....+ Am xm + 1 x1 |
+ 2 x2 +...+ m xm |
||||||||||||||||
boladı. Demek, berilgen funkciya x0 Rm noqatta differenciallanıwshı.► |
||||||||||||||||||
|
Eger |
f (x) funkciya E Rm kópliktiń hár bir noqattında differenciallanıwshı |
||||||||||||||||
bolsa, onda funkciya E kóplikte differenciallanıwshı delinedi. |
|
|
|
|||||||||||||||
|
1-teorema. Eger f (x) |
funkciya x0 E Rm noqatta differenciallanıwshı |
||||||||||||||||
bolsa, onda funkciya usı noqatta úzliksiz boladı. |
|
|
|
|
|
|
||||||||||||
|
2-teorema. Eger |
f (x) funkciya x0 |
noqatta differenciallanıwshı bolsa, onda |
|||||||||||||||
funkciya usı noqatta barlıq dara tuwındılarǵa iye hám |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
f x' (x0 )= A1, |
f x' (x0 )= A2 ,..., f x' (x0 )= Am |
|
|
||||||||||
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
m |
|
|
|
|
boladı.
201
Bul teoremadan x0 noqatta differenciallanıwshı f (x) funkciyanıń ósimi
ushın
f (x0 )= fx'1 (x0 ) x1 + fx'2 (x0 ) x2 +...+ fx'm (x0 ) xm +0( )
kelip shıǵadı.
Eskertiw. f (x) funkciyanıń bazıbir x0 noqatta barlıq dara tuwındıları
fx'1 (x0 ), fx'2 (x0 ), fx'3 (x0 ),..., fx'm (x0 ) nıń bar bolıwınan, onıń usı noqatta differenciallanıwshı bolıwı hár dayım kelip shıǵabermeydi.
Joqarıda keltirilgen teorema hám eskertiwden f (x) funkciyanıń x0 noqatta
barlıq dara tuwındılarǵa iye bolıwı funkciyanıń usı noqatta differenciallanıwshı bolıwınıń zárúriy shárti ekenligi kelip shıǵadı.
Meyli f (x) funkciya E Rm |
kóplikte berilgen bolıp, U (x0 ) E bolsın. |
||||||||||||||||||||
3-teorema. Eger |
|
f (x) |
funkciya U (x0 ) da barlıq dara tuwındılarǵa iye |
||||||||||||||||||
bolıp, bul dara tuwındılar |
x0 noqatta úzliksiz bolsa, onda |
f (x) funkciya x0 |
|||||||||||||||||||
noqatta differenciallanıwshı boladı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Bul teorema f (x) |
funkciyanıń x0 |
noqatta differenciallanıwshı bolıwınıń |
|||||||||||||||||||
jetkilikli shártin ańlatadı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Quramalı funkciyanıń tuwındısı. Meyli |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
x1 = 1 (t )= 1 (t1 ,t2 ,...,tk ) |
|
, |
|
|
|
|
||||||||||
|
|
|
|
|
x2 = 2 (t )= 2 (t1 ,t2 ,...,tk ) |
, |
|
|
|
|
|||||||||||
|
|
|
|
|
........................................... |
|
|
|
|
||||||||||||
|
|
|
|
|
xm = m (t )= m (t1 ,t2 ,...,tk ) |
|
|
|
|
||||||||||||
funkciyalardıń hár bir M Rk |
kóplikte u = f (x , x |
,..., x |
|
) funkciya bolsa, onda |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 2 |
|
|
|
m |
|
|
|
|
||
|
( |
|
|
|
|
) |
|
|
|
( |
) |
|
|
( |
|
) |
|
|
|
( |
) |
E = |
|
x , x ,..., x |
|
Rm ; x |
= |
t |
|
, x |
= |
|
t |
|
,...., x |
= |
t |
|
|||||
|
|
1 |
2 |
m |
|
|
1 |
1 |
|
|
2 |
2 |
|
|
|
|
m |
m |
|
||
kóplikte berilgen bolıp, olar arqalı f ( 1 (t), 2 (t),..., m (t))=F (t1 ,t2 ,...,tk ) quramalı funkciya payda bolsın.
202
4-teorema. |
Eger |
|
xi = i (t1 ,t2 ,...,tk ) |
funkciyalarnıń |
hár |
biri |
|||||||||||||||||||||||||||||||
(i =1, 2,....m), |
(t10 ,t20 ,...,tk0 ) M noqatta differenciallanıwshı bolıp, f (x1 , x2 ,..., xm ) |
||||||||||||||||||||||||||||||||||||
funkciya sáykes (x10 , x20 ,..., xm0 ) noqatta |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
(x10 = 1 (t10 ,t20 ,...,tk0 ), x20 |
|
= 2 (t10 ,...,tk0 ),..., xm0 = m (t10 ,...,tk0 )) |
|
|
|||||||||||||||||||||||||||||||
differenciallanıwshı bolsa, onda quramalı f |
( 1 (t1 ,...,tk ), 2 (t1 ,..., tk ),..., m (t1 ,..., tk )) |
|
|||||||||||||||||||||||||||||||||||
funkciya (t10 ,t20 ,...,tk0 ) |
noqatta differenciallanıwshı boladı. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Meyli |
f (x (t)) quramalı |
|
|
funkciya |
|
|
joqarıdaǵı |
teoremanıń |
shártlerin |
||||||||||||||||||||||||||||
qanaatlandırsın. Onda |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
f (t)= |
f |
|
|
|
|
t |
+ f t |
|
+... + |
f |
t |
|
+ 0( ) |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
t |
|
|
1 |
|
t |
2 |
|
|
|
2 |
|
|
t |
k |
|
|
|
|
k |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
boladı. Bunan quramalı funkciyanıń dara tuwındıları tómendegishe |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
f = |
f |
|
|
|
|
x1 |
+ |
|
f |
|
x2 |
+ ... + |
f |
|
|
|
xm |
, |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
t1 |
|
x1 t1 |
|
|
|
x2 t1 |
|
|
xm t1 |
|
|
|
|
|
||||||||||||||||||||
|
|
|
f |
= |
f |
|
|
|
|
x1 |
+ |
|
f |
|
x2 |
+ ... + |
f |
|
|
|
xm |
, |
|
|
|
|
|||||||||||
|
|
|
t2 |
x1 t2 |
|
x2 t2 |
xm t2 |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
................................................................... |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
f |
= |
f |
|
|
|
|
x1 |
+ |
|
f |
|
x2 |
+ ... + |
f |
|
|
|
|
xm |
|
|
|
|
|
||||||||||
|
|
|
tk |
x1 tk |
|
x2 tk |
xm tk |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
bolıwı kelip shıǵadı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Meyli |
m = 2 |
|
bolsın. |
|
Onda |
|
|
|
|
|
eki |
|
|
ózgeriwshili |
u = f (x, y) |
||||||||||||||||||||||
((x, y) E R2 , |
u R) funkciyanıń dara tuwındıları |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
f |
= lim |
x f |
= lim |
|
f (x + x, y)− f (x, y) |
, |
|
|
||||||||||||||||||||||||||
|
|
|
x |
|
|
|
|
x |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
x→0 |
|
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
f |
= lim |
|
|
y f |
|
= lim |
|
f (x, y + y)− f (x, y) |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
y |
|
|
|
|
y |
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
y→0 |
|
|
|
|
|
y→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
hám
f = f (x + x , y + y)− f (x, y)= A x + B y + 1 x + 2 y
differenciallanıwshılıq shártine iye bolamız.
203

2-mısal. f (x, y)=lntg |
|
x |
|
funkciyanıń dara tuwındılarin tabıń. |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
◄Berilgen funkciyanıń dara tuwındıları tómendegishe boladı |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
f |
|
|
x |
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
= |
|
|
lntg |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
x y |
|
|
|
|
|
|
|
|
|
|
|
2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
x |
y |
|
tg |
|
|
|
|
cos |
2 |
|
|
|
|
|
y sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
f |
|
|
x |
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
− 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
= |
|
|
lntg |
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
► |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
y |
|
|
|
|
y |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
y |
|
|
|
tg |
|
|
|
|
|
|
cos |
|
|
|
|
|
|
|
y |
|
|
|
|
|
y |
2 |
sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
3-mısal. f (x, y)= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
x2 + y2 funkciyanıń dara tuwındıların tabıń. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
◄Meyli (x, y) (0,0) bolsın. Onda |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
= |
|
|
|
|
|
|
x2 |
|
|
+ y2 = |
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
, |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
x |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 x2 + y 2 |
|
|
|
|
|
x2 + y2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
x2 |
|
+ y 2 = |
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
y |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 x2 + y 2 |
|
|
|
x2 + y 2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
boladı. Meyli (x, y)=(0,0) bolsın. Anıqlamaǵa kore |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
f (0,0)= lim |
|
|
f (0 + x,0)− f (0,0) |
= lim |
|
|
|
x |
|
, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→0 |
|
x |
|
|
|
|||||||||||||||||||||
|
|
|
|
f (0,0) |
= lim |
|
|
f (0,0 + y)− f |
(0,0) |
= lim |
|
|
y |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
y |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y→0 |
|
|
|
|
|||||||||||||||||||||||||||
bolıp, bul limitlerge iye emesligi sebebli berilgen funkciya (0,0) noqatta dara tuwındılarǵa iye bolmaydı.►
4-mısal. Eger |
|
f (x, y) |
funkciya |
R 2 |
differenciallanıwshı bolıp, |
||||||||||
x = r cos , y = r sin |
bolsa, onda |
f |
, |
f |
tabıń. |
|
|
|
|
||||||
r |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
◄ Meyli |
f (x, y) = f (r cos , r sin ) quramalı funkciyanıń dara tuwındıların tabıw |
||||||||||||||
qaǵıydasına muwapıq |
|
|
|
|
|
|
|
|
|
|
|
|
|||
f |
= f |
x |
+ f |
|
y = cos |
f |
+ sin |
f = |
|
1 |
|
(x f |
+ y f ), |
||
|
|
|
|
|
|||||||||||
|
|
|
|||||||||||||
r |
x |
r |
y |
r |
x |
|
|
|
y |
x2 + y 2 |
|
x |
y |
||
204
|
f |
= |
f |
|
x |
+ |
f |
|
|
y |
= −r sin |
f |
+ r cos |
f |
= −y |
f |
+ x |
f |
. |
► |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
x |
|
y |
|
x |
|
y |
|
|
x |
|
y |
|
||||||
|
|
|
|
|
|
|
|
|
|
11.2. Baǵıt boyınsha tuwındı |
|
|
|
|
|||||||
Meyli |
f (x, y) funkciyanıń tegisliktegi qálegen baǵıtı boyınsha tuwındısı |
||||||||||||||||||||
túsinigin |
keltiremiz. |
f (x, y) funkciya |
E R2 kóplikte berilgen |
bolsın. Bul |
|||||||||||||||||
funkciyanı |
Dekart |
|
koordinatalar |
sistemasında |
A0 =(x0 , y0 ) |
noqattıń |
|||||||||||||||
U (A0 ) E,( 0) dógerende qaraymız. |
A =(x, y) U |
|
(A ) noqattı alıp , A hám |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
A noqatları arqalı tuwrı sızıq ótkizemiz. Ondaǵı eki baǵıttan birine óń baǵıt (26sızılmada kórsetilgen), ekinshisini bolsa teris baǵıt dep qabıl qılamız. Bul baǵıtlanǵan tuwrı sızıqtı l menen belgileymiz. A0 hám A noqatlar arasındaǵı aralıq
= (A0 , A)= 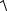
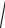 (x − x0 )2 + (y − y0 )2
(x − x0 )2 + (y − y0 )2
bolıp, bul aralıq A0 A vektorınıń baǵıtı l nıń baǵıtı menen birdey bolsa, óń belgi menen keri jaǵdayda teris belgi menen alınadı.
y
|
|
|
|
|
l |
y |
|
|
|
• A |
|
|
|
|
|
|
|
y0 |
|
• |
A0 |
• |
|
0 |
|
|
|
|
|
|
|
x0 |
|
x |
x |
|
|
|
|
|
|
|
26-sızılma |
|
|||
|
|
|
|||
Eger l nıń óń baǵıtı menen |
OX |
hám OY |
koordinata kósherlerinıń óń |
||
baǵıtıları arasındaǵı múyeshti sáykes túrde |
hám |
delinse, (26-sızılma) onda |
|||
205
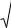
|
|
|
|
|
|
|
|
|
|
|
|
|
x − x0 |
|
= cos , |
y − y0 |
= cos |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
kelip shıǵadı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1-anıqlama. Eger lim |
f (A)− f (A0 ) |
limit bar bolsa, onda bul limit |
f (x, y) |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
A→A0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
funkciyanıń A0 =(x0 , y0 ) noqattaǵı l |
|
|
baǵıt boyınsha tuwındı delinedi. Onı |
|
||||||||||||||||||||||||||||||||
f (A0 ) yamasa f (x0 , y0 ) arqalı belgilenedi. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
l |
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Demek, |
f (A0 ) |
= lim |
f (A)− f (A0 ) |
. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
A→A0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
1-teorema. Eger |
f (x, y) funkciya A0 = (x0 , y0 ) noqatta differenciallanıwshı |
|||||||||||||||||||||||||||||||||||
bolsa, onda funkciya usı noqatta hár qanday baǵıt boyınsha tuwındıǵa iye hám |
||||||||||||||||||||||||||||||||||||
|
f (A0 ) |
= f (x0 , y0 )= f (x0 , y0 )cos + f (x0 , y0 )cos |
(5) |
|||||||||||||||||||||||||||||||||
|
l |
|
|
|
|
|
|
l |
|
|
|
|
|
|
x |
|
|
|
y |
|
||||||||||||||||
boladı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
◄ Meyli |
f (x, y) |
funkciya A0 = (x0 , y0 ) noqatta differciallanıwshı bolsın. |
||||||||||||||||||||||||||||||||||
Onda f (A)− f (A0 )= f (x, y)− f (x0 , y0 ) ósimi ushın |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
f (A)− f |
(A |
)= |
f (A0 ) |
|
(x − x |
|
|
)+ |
f (A0 ) |
(y − y |
|
|
)+ 0( ) |
|
|||||||||||||||||||||
|
|
|
0 |
|
|
0 |
|
|||||||||||||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
boladı, bunda = |
|
(x − x0 )2 + (y − y0 )2 . |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
Keyingi teńliktiń hár eki tárepinen ǵa bólemiz |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
f (A)− f (A0 ) |
= f (A0 ) |
|
x − x0 |
|
+ f (A0 ) |
y − y0 |
|
+ |
0( ) |
. |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
||||||||||||
Bizge belgili |
|
|
|
x − x0 |
= cos , |
y − y0 |
= cos |
esapqa alıp , → 0 да limitke |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
ótip, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
f (A)− f (A0 ) |
|
= f (A0 )cos + f (A0 )cos . |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
→0 |
|
|
|
|
|
|
|
x |
|
|
|
y |
|
|||||||||||||||||||
Demek, f (A0 ) = f (x0 , y0 )cos + f (x0 , y0 )cos .► |
|
|||||||||||||||||||||||||||||||||||
|
|
l |
|
x |
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|||||||||||||||
206

2-mısal. f (x, y)= x2 + y2 funkciyanıń (1,1) |
|
|
|
|
→ |
→ |
→ |
||||||||||||||||||||||||
noqatta r |
= i |
+ 2 j vektor |
|||||||||||||||||||||||||||||
baǵıt boyınsha tuwındısın tabıń. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
◄ cos = |
1 |
|
, cos = |
|
2 |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
5 |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
f (x, y) |
= |
|
(x2 + y |
2 ) |
=2 x , |
f (1,1) |
= 2 , |
|
|
|||||||||||||||||||||
|
|
|
|
x |
|
|
|
|
|
x |
|
|
|
|
x |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
f (x, y) |
= |
|
(x2 + y |
2 ) |
=2 y, |
f (1,1) |
= 2 , |
|
|
|||||||||||||||||||||
|
|
|
|
y |
|
|
|
|
y |
|
|
|
|
y |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
boladı. (5) formuladan paydalanamız |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
f (1,1) = 2 |
1 |
|
|
+ 2 |
2 |
|
|
= |
|
6 |
|
.► |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
l |
5 |
|
|
|
|
5 |
|
|
|
|
5 |
|
|
|
|
|
|||||||||||
Meyli f (x, y) funkciya ashıq E R2 |
kóplikte differenciallanıwshı bolsın. |
||||||||||||||||||||||||||||||
Bul funkciya E kópliktıń hár bir (x, y) E noqattında |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
f (x, y), |
|
|
f (x, y) |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
y |
|
|
|
|
|
|
|
|
|
||||||||||
dara tuwındılarǵa iye boladı. Koordinataları sol dara tuwındılardan ibarat bolǵan vektordı dúzemiz
|
f |
(x, y) → |
f |
(x, y) |
→ |
(6) |
|
|
i + |
|
|
j |
|
|
x |
y |
|
|
||
→ |
→ |
|
|
|
|
|
bunda, i hám |
j koordinata kósherleri boyınsha baǵıtlanǵan birlik vektorlar. (6) |
|||||
vektor f (x, y) funkciyanıń gradienti delinedi hám grad f arqalı belgilenedi |
||||||
|
|
grad f = |
f (x, y) → |
f (x, y) → |
||
|
|
|
i + |
j . |
||
|
|
|
|
x |
|
y |
Demek, |
grad f |
E kópliktıń hár bir (x, y) noqatına bir vektor sáykes |
||||
qoyıwshı qaǵıyda, basqasha aytqanda eki ózgeriwshili vektor funkciya boladı.
207

f (x, y) funkciyanıń |
→ |
= (cos , cos ) vektor baǵıtı boyınsha |
f (x, y) |
e |
|||
|
|
|
l |
|
|
|
→ |
tuwındısın onıń gradienti arqalı ańlatıw mumkin.Haqıyqatanda grad f |
hám e |
||||||||||||||||
vektorlarınıń skalyar kóbeymesi |
|
|
|
|
|||||||||||||
|
|
|
→ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e grad f =cos f (x, y)+ cos f (x, y) |
|
(7) |
||||||||||||
|
|
|
|
|
|
|
|
x |
|
y |
|
|
|||||
bolıp, ol (5) formuladan |
f (x, y) ǵa teń boladı |
|
|
||||||||||||||
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→ |
|
f (x, y). |
|
|
|||||
|
|
|
|
|
|
|
|
e grad f = |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
→ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e hám |
grad f |
vektorlarınıń skalyar kóbeymesi usı vektor uzınlıqları |
|||||||||||||||
kóbeymesin olar arasındaǵı múyesh kosinusǵa kóbeymesine teń boladı |
|
||||||||||||||||
|
|
|
→ |
|
|
|
|
grad f |
|
|
|
→ |
|
→ |
|
(8) |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
e grad f = |
|
|
e |
|
cos e , grad f |
|||||||||
|
→ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Bunnan |
e |
|
=1. (7) hám (8) qatnaslardan |
|
|
||||||||||||
|
|
|
f |
(x, y) |
= |
|
grad f (x, y) |
|
|
→ |
|
|
|||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
l |
|
|
|
cos e , grad f |
(x, y) |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→
kelip shıǵadı. Keyingi teńlikten, e hám grad f (x, y) vektorlar parallel bolǵanda
f (x, y) nıń mánisi eń úlken hám ol
l
grad f (x, y) =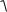
 f x'2 (x, y)+ f y'2 (x, y)
f x'2 (x, y)+ f y'2 (x, y)
teń boladı. Sonday etip, f (x, y) funkciyanıń gradienti grad f funkciyanıń (x, y) noqattaǵı eń tez ósetuǵın tárepke baǵıtlanǵan bolıp, onıń uzınlıǵı usı baǵıt boyınsha ósiw tezligine teń eken.
3-mısal. f (x, y)= x2 + 2 y2 funkciyanıń (1,1 ) noqatta eń tez ósetuǵın baǵıtı anıqlansın hám usı baǵıt boyınsha ósiw tezligin tabıń.
208
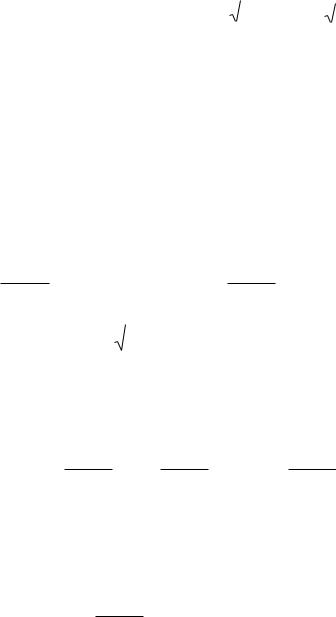
◄ |
f (x, y) |
|
= |
(x2 + 2 y2 ) |
|
= 2x, |
f (1,1 ) |
= |
2; |
|
f (x, y) |
= |
(x2 + 2 y2 ) |
|
= |
|
4 y, |
f ( |
1,1 ) |
= 4; |
|||||||||||||||||||||||||||||||
x |
|
|
x |
|
|
x |
|
|
|
|
y |
|
|
|
|
y |
|
|
|
|
|
|
|
y |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
→ |
|
→ |
|
|
|
|
|
|
|
|
(1,1 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
bolıp, grad f (1,1 )=2 i + |
4 j |
, |
|
grad f |
= |
|
|
|
22 + 42 =2 |
|
5 boladı.► |
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
11.3. Kóp ózgeriwshili funkciyanıń differencialı |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
Meyli |
|
f (x)= f (x1 , x2 , , xm ) |
funkciya |
|
E Rm |
|
|
да |
berilgen bolıp, |
|||||||||||||||||||||||||||||||||||||||||
x0 = (x10 , x20 , , xm0 ) E |
|
noqatta differenciallanıwshı bolsın. Onda anıqlamaǵa |
|||||||||||||||||||||||||||||||||||||||||||||||||
kóre funkciyanıń x0 noqattaǵı tolıq ósimi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
f (x0 )= |
f (x0 ) x1 + |
f (x0 ) |
x2 |
+ + |
|
f (x0 ) xm + o( ) |
|
|
(1) |
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
x |
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
boladı. Bul |
|
qatnastan |
= |
|
|
x |
2 |
+ x |
2 + + x2 |
bolıp, |
|
|
|
x → 0, |
x |
2 |
→ 0 , |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||||
..., xm → 0 |
da |
→ 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1-anıqlama. f (x) funkciyanıń f (x0 ) ósimidegi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
f (x0 ) x + |
f (x0 ) x |
2 |
|
+ + |
f (x0 ) x |
m |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
1 |
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
xm |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
ańlatpa f (x) funkciyanıń x0 |
noqattaǵı differencialı delinedi hám |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
df (x0 ) yamasa df (x10 , x20 , , xm0 ) arqalı belgilenedi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
df (x0 )= |
f (x0 ) x1 |
+ |
f (x0 ) |
x2 |
+ + |
f (x0 ) |
xm . |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
x |
m |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Demek, |
|
f (x) funkciyanıń |
x0 |
noqattaǵı differencialı x , x |
, , x |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
m |
baylanıslı hám olardıń sızıqlı funkciyası boladı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
Eger |
x1 = dx1 , x2 = dx2 , , xm = dxm bolsa, onda |
|
|
f (x) funkciyanıń |
||||||||||||||||||||||||||||||||||||||||||||||
x0 noqattaǵı differencialı |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
df (x0 )= |
f (x0 )dx1 + |
|
f (x0 )dx2 |
+ + f (x0 )dxm |
|
|
|
|
(2) |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
x |
m |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
209
