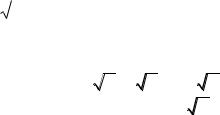|
|
(a)= B |
(a) B0 |
(a) |
|
|
|
Bunnan |
B |
boladı. |
|
|
r |
r |
r |
|
|
|
Rm keńislikte noqattıń |
dógeregi. Bazı bir |
x0 = (x10 , x20 ,..., xm0 ) Rm |
noqat |
hám 0 san berilgen bolsın. |
|
|
|
1-anıqlama. Orayı |
x0 |
noqatta radiusı |
bolǵan Rm keńislikte |
shar, |
x0 Rm noqattıń sferalıq dógeregi delinedi hám U (x0 ) arqalı belgilenedi:
U (x0 )= x Rm : (x, x0 ) .
Rm keńislikte ashıq hám tuyıq kóplikler. Meyli Rm keńislikte bazı bir G kóplik (G Rm ) berilgen bolıp, x0 G bolsın.
Eger x0 noqat G kóplikke tiyisli bolǵan U (x0 ) dógerekke iye bolsa, onda
(U (x0 ) G) x0 noqat G kópliktiń ishki noqatı delinedi.
2-anıqlama. G kópliktiń hár bir noqatı onıń ishki noqatı bolsa, ol ashıq kóplik delinedi.
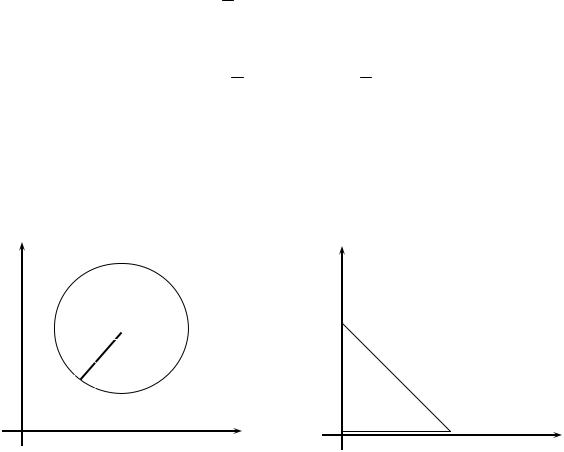
1-mısal. Rm keńisliktegi Br (a)= x Rm : (x,a) r shardıń ashıq kóplik ekenin kórsetiń.
◄ x0 Br (a) noqattı alamız. Onda r − (x0 ,a) shama oń boladı. Onı deymiz
= r − (x0 ,a) (22-sızılma).
a
r
22-sızılma

Endi x0 noqattıń
U (x0 )= x Rm : (x, x0 ) dógeregin qaraymız.Bunda U (x0 ) Br (a) boladı. Haqıyqatan da,
x U (x0 ) (x, x0 ) bolıp, aralıqtıń 3)-qáseytine muapıq
(x,a) (x, x0 )+ (x0 , a) + (x0 ,a)= r
boladı. Demek,
x U (x0 ) x Br (x0 )
Bunnan U (x0 ) Br (x0 ) kelip shıgadı.
Demek, Br (a) kópliktiń hár bir noqatı onıń ishki noqatı boladı. Onda Br (a) ashıq kóplik.►
Meyli F Rm kóplik hám x0 Rm noqat berilgen bolsın. Eger x0 noqattıń qálegen U (x0 ) dógereginde ( 0) F kópliktiń x0 den parıqlı keminde bir noqatı bolsa, onda x0 noqatı F kópliktiń limit noqatı delinedi.
Máselen, Br (a)= x Rm : (x, a) r kópliktiń hár bir noqatı onıń limit noqatı boladı. Al Br0 = x Rm : (x, a)= r kópliktiń barlıq noqatları da usı Br (a)
kópliktiń limit noqatı boladı. Biraq, bul limit noqatlar Br (a) kóplikke tiyisli bolmaydı.
3-anıqlama. Eger F Rm kópliktiı barlıq limit noqatları usı kóplikke tiyisli bolsa, onda F tuyıq kóplik delinedi.
Máselen, Br (a)= x Rm : (x, a) r kóplik ( Rm keńisliktegi tuyıq shar) tuyıq kóplik boladı.
Bazı bir M Rm kóplik hám x0 Rm noqattı qarayıq.
Eger x0 noqattıń qálegen U (x0 ) dógereginde M kópliktiń hám Rm \ M
kópliktiń noqatları bolsa, onda x0 noqat M kópliktiń shegaralıq noqatı delinedi.
M kópliktiń barlıq shegaralıq noqatları onıń shegarası boladı. M kópliktiń shegarası (M ) arqalı belgilenedi. Máselen, Br0 (a)= x Rm : (x, a)= r
kóplik
Br (a)= x Rm : (x, a) r kópliktiń shegarası boladı (Br (a))= Br0 (a).
Eger F Rm kópliktiń shegarası (F ) usı kóplikke tiyisli bolsa, onda F tuyıq kóplik boladı. Máselen, Br (a)= x Rm : (x,a) r tuyıq kóplik boladı, sebebi
(Br (a))= Br0 (a) Br (a).
4-anıqlama. Eger M Rm kóplik ashıq hám baylamlı kóplik bolsa, ol oblast delinedi.
Máselen, Br (a)= x Rm : (x, a) r oblast boladı.
(x0 , y0 )
1
r
1
23-sızılma
10.2. Rm keńislikte izbe-izlik hám onıń limiti |
Meyli bazı bir qaǵıydaǵa muapıq hár bir натурал san n ge Rm keńisliktiń |
tek bir |
|
|
|
x(n) = (x(n) |
, x(n) |
,..., x(n)) |
(n =1,2,...) |
1 |
2 |
m |
|
noqatı sáykes qoyılǵan bolsın. Bul sáykeslik nátiyjesinde Rm keńisliktiń noqatlarınan payda bolǵan
(x(1) |
, x(1) |
,..., x |
(1)) |
, |
(x |
(2) |
, x(2),..., x(2)) |
, ... , |
(x(n) |
, x(n),..., x(n)) |
, ... |
1 |
2 |
|
m |
1 |
2 |
|
m |
1 |
2 |
m |
qısqasha |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x(1) , x(2) ,..., x(n) ,... |
|
|
|
|
kóplik boladı. Onı R(m) |
keńislikte izbe-izlik деб, x (n) arqalı belgilenedi. Demek, |
x (n) izbe-izliktiń |
aǵzaları |
Rm |
keńisliktiń noqatlarınan |
ibarat bolıp, bul |
noqatlardıń koordinataları m та |
|
|
|
|
|
|
|
|
|
|
x1(n) , |
|
x2(n) , |
... |
xm(n) , |
( n =1,2,..) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sanlar izbe-izliklerin júzege keltiredi. |
|
|
|
|
|
|
|
Meyli Rm keńislikte x( n) : |
|
|
|
|
|
|
|
|
|
|
|
|
x(1) , |
x(2) , ....., x(n) ,.... |
|
|
|
(1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
izbe-izlik hám
a = (a1, ,a2 ,...am ) Rm
noqatı berilgen bolsın.
1-anıqlama. Eger 0 alǵanda, sonday n0 N san tabılıp, barlıq n n0
ushın
(x(n) , a)
yaǵniy
0, |
n N, |
n n : |
(x(n) , a) |
|
0 |
0 |
|
bolsa, onda a noqatı x (n) izbe-izliktiń limiti delinedi hám
lim x(n) = a |
→ da x(n) → a |
n→ |
yamasa n |
arqalı belgilenedi. n n0 |
da |
|
|
(x(n) , a) |
teńsizliktiń orınlanıwı, (1) izbe-izliktiń n0 dan úlken nomerli aǵzaları a noqat tıń |
U (a) dógeregine tiyisli bolıwın bildiredi. |
|
2-anıqlama. Eger |
a Rm noqattiń |
qálegen U (a) dógeregi alınǵanda, |
x (n) izbe-izliktiń bazı bir aǵzasınan keyingi barlıq aǵzaları usı dógerekke tiyisli
bolsa, onda a noqat |
x (n) izbe-izliktiń limiti delinedi. |
|
|
|
|
|
|
|
|
|
|
(n) |
1 |
|
1 |
|
1 |
|
|
|
|
|
|
|
|
x |
|
= |
|
, |
|
, ... |
|
|
|
|
|
|
|
|
|
|
|
|
|
1-mısal. |
Rm |
keńislikte |
|
|
|
|
|
n |
|
n |
|
n izbe-izliktiń limiti |
a = (0,0, ,0) ekenligin kórsetin. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n0 |
|
|
m |
+1 |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
alamız. Onda n n0 ushın |
◄ 0 sanın alıp, |
|
|
|
|
|
|
|
|
( x(n) , a) = (( |
1 |
, |
1 |
,..., |
1 |
), (0, 0,..., 0)) = |
|
m |
|
|
m |
|
|
|
|
|
|
|
|
n |
|
n |
|
n |
n |
|
n0 |
boladı. Demek,
lim x(n) = a
n→ .►
Meyli Rm keńislikte x (n) izbe-izlik hám a Rm noqat berilgen bolsın.
1-teorema. Eger Rm keńislikte x(n) = (x1(n), x2(n),..., xm(n)), (n =1, 2,...)
izbe-izlik a = (a1,a2 ,....,am ) limitke iye bolsa, onda
185
lim x |
(n ) = a , |
|
n→ |
1 |
1 |
|
|
|
|
|
|
|
|
lim x |
(n ) = a |
2 |
, |
n→ |
|
2 |
|
|
|
|
|
|
|
|
|
................... |
|
|
lim x |
(n ) = a |
m |
, |
n→ |
|
m |
|
|
|
|
|
|
|
|
boladı.
2-teorema. Eger Rm keńisliktegi |
|
xn = |
|
x(n) , x(n) ,..., x(n) |
) |
,(n =1, 2...) |
|
|
|
|
|
|
( |
m |
|
|
|
|
|
|
1 2 |
|
izbe-izlik hám a = (a1,a2 ,....,am ) noqatı ushın |
|
|
|
|
|
|
|
lim x(n) = a , |
|
|
|
|
|
|
n→ |
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim x2(n) |
= a2 , |
|
|
|
|
|
|
n→ |
|
|
|
|
|
|
|
|
|
|
....................... |
|
|
|
|
|
lim xm(n) |
= am |
|
|
|
|
|
|
n→ |
|
|
|
|
|
|
|
|
bolsa, onda x |
(n) |
izbe-izlik limitine iye bolıp |
lim x(n) = a, |
boladı. |
|
n→ |
Bul teoremalardan tómendegiler kelip shıgadı.
keńislikte |
x(n) = ( x1(n) , |
x2(n) , ...., xm(n) ) izbe-izlik |
,..., a ) lim x m limitke n→
(n) = a iye bolıwı ushın
lim x(n) = a ,
n→ 2 2
.......................
lim x(n) = a ,
n→ m m
bolıwı zárúrli hám jetkilikli.
Eger (1) izbe-izlik limitke iye bolsa, onda jıynaqlı izbe-izlik delinedi.
3-anıqlama. Rm keńislikte x (n) izbe-izlik berilgen bolsın. Eger |
0 |
hám sonday n0 |
N tabılıp n n0 , p n |
ushın |
|
|
0 |
|
|
( x(n ) , x( p ) )
teńsizlik orınlı bolsa, onda x (n) fundamental izbe-izlik delinedi.
3-teorema (Koshi teoreması). x( n) izbe-izliktiń jıynaqlı bolıwı ushın onıń
fundamental bolıwı zárúrli hám jetkilikli. |
|
Dara izbe-izlikler. |
Rm |
keńislikte |
x (n) |
|
|
: |
|
|
x(1), x(2), , x(n), |
izbe-izlik berilgen bolsın. Bul izbe-izlik |
|
|
|
|
x(n1 ), x(n2 ), |
..., x(nk ) ,..., |
Bunda, |
|
|
|
|
n1 n2 |
... nk ...; nk N, k =1,2,.., |
|
|
|
|
|
|
|
berilgen x (n) izbe-izliktiń dara izbe-izligi |
delinedi. Onı x(nk ) arqalı belgilenedi. |
Eger x |
( n) |
izbe-izlik jıynaqlı bolıp, |
lim x(n ) = a |
|
n→ |
bolsa, bul izbe-izliktiń hár |
qanday dara izbe-izligi x |
(nk ) |
|
lim x |
(nk ) = a |
|
da jıynaqlı bolıp, k → |
boladı. |
Meyli Rm keńislikte bazı bir M kóplik berilgen bolsın M R m . Eger Rm |
keńislikte orayı (0, 0,..,0) Rm , radiusı r 0 bolǵan shar
U 0 = (x1, x2 ,..., xm ) Rm : ((x1, x2 ,.., xm ,) (0,0,...0)) r M U 0 bolsa, onda M shegaralanǵan kóplik delinedi.
5-teorema (Boltsano-Veyershtrass). Rm keńislikte hár qanday shegaralanǵan izbe-izlikten jıynaqlı dara izbe-izlik ajıratıp alıw múmkin.
10.3. Kóp ózgeriwshili funkciya hám onıń limiti
Meyli Rm keńislikte E kóplik berilgen bolsın E R m .

1-anıqlama. Eger E kópliktegi hár bir x = (x1, x2 ,...xm ) noqatqa bazı bir f qaǵıydaǵa kóre bir haqıyqıy u sanı sáykes qoyılǵan bolsa, onda E kóplikte kóp ózgeriwshili ( m ózgeriwshili) funkciya berilgen delinedi. Onı
f : x = (x1, x2 ,..., xm ) →u yamasa u = f (x) = f (x1, x2 ,..., xm )
(x = (x1 , x2 ,..., xm ) Rm , u R)
arqalı belgilenedi. Bunda E funkciyanıń anıqlanıw kópligi, x1, x2 ,..., xm lar (erkli
ózgeriwshiler) funkciya argumentleri, u bolsa x1, x2 ,..., xm lardıń funkciyası delinedi. Máselen, f - hár bir
x = (x1 , x2 ,...xm ) M ,
M = x R m : (x,0) 1
noqatqa bul
(x1 , x2 ,..., xm ) → 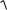
 1 − x12 − x22 − ... − xm2
1 − x12 − x22 − ... − xm2
qaǵıyda menen bir haqıyqıy u |
sanın sáykes qoysın. Onda M Rm |
kóplikte |
anıqlanǵan |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u = |
1 − x2 |
− x2 |
− ... − x2 |
|
|
|
|
|
|
|
1 |
2 |
m |
|
|
|
funkciya payda boladı. |
|
|
|
|
|
|
|
Meyli |
u = f (x1, x2 ,...xm ) |
funkciya |
E Rm |
kóplikte |
berilgen |
bolsın. |
x0 = (x10 , x20 ,..., xm0 ) E noqatqa sáykes keliwshi u0 san u = f (x) |
funkciyanıń x0 |
noqattaǵı menshikli mánisi delinedi u0 = f (x0 ). |
|
|
|
Berilgen funkciyanıń barlıq menshikli mánislerinen ibarat bul |
|
|
|
|
|
|
u = f (x) : x E |
|
|
(1) |
|
|
|
|
|
|
|
|
|
sanlar kópligi |
u = f (x) |
funkciyanıń mánisler kópliǵi delinedi. Eger (1) kóplik |
shegaralanǵan |
bolsa, |
onda u = f (x) = f (x1, x2 ,...xm ) funkciya E |
kóplikte |
shegaralanǵan delinedi. |
|
|
|
|
|
|
|
Meyli |
f (x1, x2 ,...xm ) funkciyada |
|
|
|
|
x1 = 1 (t) = 1 (t1,t2 ,...,tk ), x2 = 2 (t) = 2 (t1,t2 ,...,tk ),
|
|
|
.......................................... |
|
|
|
|
xm = m (t) = m (t1,t2 ,...,tk ), |
bolsın, bunda i (t) funkciya (i =1,2,...,m) T Rk |
kóplikte anıqlanǵan bolıp, |
t = (t1,t2 ,...,tk ) T |
bolǵanда oǵan sáykes |
x = (x1, x2 ,...xm ) E bolsın. nátiyjede |
|
f (x(t)) = f ( 1(t1,...,tk ), 2 (t1,...,tk ),...., m (t1,...,tk )) = F(t1,t2 ,...,tk ) |
funkciya payda boladı. Onı quramalı funkciya delinedi. |
Kóp |
ózgeriwshili funkciyanıń |
eseli |
limiti. Meyli f (x) funkciya E Rm |
kóplikte berilgen, |
x0 Rm noqat E nıń limit noqatı bolsın. Onda Rm keńislikte |
sonday |
x |
(n) |
|
|
|
|
|
: |
|
|
|
|
|
|
|
x(1) , x(2) ,...., x(n) ,.... |
|
izbe-izlik tabılıp: |
|
|
|
|
|
|
|
1) n N да x(n) E, |
x(n) x0 , |
|
|
|
2) n → |
да x(n) → x0 |
|
boladı. |
|
|
|
|
|
|
2-anıqlama (Geyne). Eger
|
|
1) |
n N да x(n) E, |
x(n) x0 ; |
|
|
|
|
2) |
n → |
|
да x(n) → x0 |
|
|
|
|
shartlerin qanaatlandırıwshı qálegen x(n) izbe-izlik ushın |
|
|
|
|
|
|
n → |
|
да f (x(n) ) → A |
|
|
|
bolsa, onda |
A |
f (x) = f (x , x ,...., x |
m |
) |
funkciyanıń |
x0 = (x0 |
, x0 |
,..., x0 ) |
noqattaǵı |
|
1 |
2 |
|
1 |
2 |
m |
|
|
|
lim |
f (x) = A |
|
|
|
|
limiti (eseli limiti) delinedi. Onı x→x0 |
|
yamasa |
|
|
|
|
lim f (x1 , x2 ,..., xm ) = A |
|
x |
→ x0 |
|
|
1 |
1 |
|
|
x2 → x20 |
|
|
............. |
|
|
xm → xm0 |
|
arqalı belgilenedi. |
|
|
|
Esletpe. Eger |
|
|
|
x(n) |
(x(n) E, |
x(n) x0 , n =1,2,....), |
y(n) |
( y(n) E, |
y(n) x0 , n =1,2,....) |
izbe-izlikler ushın n → da x(n) → x0 |
, y(n) → x0 bolıp, |
f (x(n) ) → A , f ( y(n) ) → B , A B
bolsa, onda f (x) funkciya x0 noqatta limitke iye bolmaydı.
3-anıqlama (Koshi). Eger 0 sanın alǵanda sonday = ( ) 0 tabılıp
0 (x, x0 ) teńsizlikti qanaatlandırıwshı x E (E Rm ) da
|
|
|
|
|
|
|
|
|
f (x) − A |
|
|
|
|
|
|
|
|
teńsizlik orınlı bolsa, onda A sanı |
f (x) |
funkciyanıń |
x0 noqattaǵı limiti (eseli |
limiti) delinedi. |
|
|
|
|
|
|
Meyli f (x) = f (x1, x2 ,...xm ) |
funkciya |
E Rm |
kóplikte berilgen bolıp, |
x0 = (x10 , x20 ,..., xm0 ) Rm noqat E kópliktiń limit noqatı bolsın. |
1-teorema (Koshi). f (x) funkciyası x0 |
noqatta limitke iye bolıwı ushın |
0 sanın alǵanda sonday 0 san tabılıp, |
|
|
x E (U (x0 ) \ x0 ) , |
x E (U (x0 ) \ x0 ) |
noqatlarda
f (x ) − f (x )
teńsizliktiń orınlı bolıwı zárúrli hám jetkilikli.
Meyli funkciya x1 → x10 limitke iye bolsın