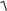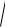Matematikaliq analiz oqiw qollanba
.pdf
|
|
|
|
|
2 (t) + 2 (t)dt |
(5) |
|
( AB) = |
|||
kelip shıǵadı. Bul formula járdeminde doǵa uzınlıǵı esaplanadı.
Aylanba bettiń maydanı hám onı esaplaw.
Meyli f (x) C[a, b] bolıp, ol [a,b] segmentte úzliksiz f '(x) tuwındıǵa
iye bolsın. Bul funkciya grafigi AB doǵanı Ox kósheri átirapında aylandırıwdan payda bolǵan П aylanba betiniń maydanın tabamız.
[a,b] segmenttiń qálegen P bóleklewin alıp, joqarıdaǵıday
n−1 |
f (x |
|
) + f (x |
|
|
) |
|
|
|
|
|
|
|
||
k |
k +1 |
(xk +1 − xk )2 +[ f (xk +1 ) − f (xk )]2 |
|||||||||||||
(K) = 2 |
|
|
|
|
|||||||||||
|
|
2 |
|
|
|
|
|||||||||
k =0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
qosındını dúzemiz. Lagranj teoremasına muwapıq |
|
|
|
||||||||||||
f (xk +1 ) − f (xk ) = f ( k )(xk +1 − xk ) = f ( k ) xk |
|||||||||||||||
boladı, bunda k [xk , xk +1 ]. Nátiyjede |
|
|
|
|
|
|
|
|
|||||||
|
|
|
n−1 |
f (x |
|
) + f (x |
|
) |
|
|
|
||||
|
|
|
k |
k +1 |
1 + f 2 ( k ) xk |
||||||||||
(K ) = 2 |
|
|
|
|
|
|
|||||||||
|
|
|
|
2 |
|
|
|
||||||||
|
|
|
k =0 |
|
|
|
|
|
|
|
|
|
|
||
boladı. Keyingi teńlikti tómendegishe jazıp alamız:
|
n−1 |
|
|
|
|
|
|
|
|
n−1 |
|
||||
|
|
|
2 |
( k ) xk + |
|
||||||||||
(K ) = 2 f ( k ) 1 + f ' |
|
|
[( f (xk ) − |
(1) |
|||||||||||
|
k =0 |
|
|
|
|
|
|
k =0 |
|||||||
− f ( k )) + ( f (xk +1 ) − f ( k ))] |
|
|
|
xk . |
|
||||||||||
1 + f '2 ( k ) |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||
f (x) C[a,b] bolǵanlıǵı sebepli f (x) |
|
1 + f '2 (x) R[a,b] |
|
||||||||||||
boladı. Demek, p → 0 da |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n−1 |
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
1 + f 2 ( k ) xk |
|
|
|
1 + f 2 (x)dx |
|
||||||||||
2 f ( k ) |
|
→ 2 f (x) |
(2) |
||||||||||||
k =0 |
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
Bunnan, 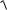
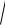 1 + f 2 (x) C [a, b].
1 + f 2 (x) C [a, b].
Demek, bul funkciya [a,b] da óziniń maksimum mánisine iye boladı. Onı
M deymiz:
M = max 1 + f 2 (x) .
a x b
170
f (x) funkciya [a,b] |
|
segmentte teń ólshewli úzliksiz boladı. Onda |
0 |
||||||||||||||||||||||||||||||||||||
alınǵanda hám, |
|
|
|
|
|
|
|
|
|
ga |
|
|
muwapıq sonday 0 |
|
san tabılsa, |
p |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
2M (b − a) |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
bolǵanda |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (xk ) − f ( k ) |
|
|
|
|
|
|
|
|
, |
|
|
f (xk +1 ) − f ( k ) |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
2M (b − a) |
2M (b − a) |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
boladı. Solardı esapqa alıp tómendegini tabamız |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
n−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||
|
|
( f (xk ) − f ( k )) + ( f (xk +1 ) − f ( k )) 1+ f |
|
( k ) xk |
|
||||||||||||||||||||||||||||||||||
|
|
k =0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
n−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
f (xk ) − f ( k ) |
|
+ |
|
f (xk +1 ) |
− f ( k ) |
|
1+ f 2 ( k ) xk |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
k =0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n−1 |
|
|
|
|
|
|
|
|
||||||||||||||
|
M |
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
xk . |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
2M (b − a) |
|
|
2M (b − a) |
|
k =0 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Bunnan p → 0 |
da kelip shıǵadı. p |
→ 0 da (1) teńlikte limitke ótip, |
|||||||||||||||||||||||||||||||||||||
(bunda (2) hám (3) qatnaslardı itibarǵa alıp) aylanba betiniń maydanı ushın |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + f 2 (x) dx . ► |
|
|
|
|
|
|
(4) |
|||||||||||||
|
|
|
|
|
|
|
|
|
(П) = 2 f (x) |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Meyli |
AB iymek sızıq joqarı yarım tegislikte jaylasqan bolıp, ol usı |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = (t) |
|
( t ) |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= (t) |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
parametrlik |
teńlemeler sisteması |
menen |
|
berilgen bolsın. Bunda (t), (t) |
|||||||||||||||||||||||||||||||||||
funkciyaları [ , ] da úzliksiz hám úzliksiz (t), (t) tuwındılarǵa iye. Bul
iymek sızıqtı Ox kósheri átirapında aylandırıwdan payda bolǵan aylanba betiniń maydanı
|
|
|
(П) = 2 (t) |
2 (t) + 2 (t) dt |
(5) |
boladı.
2-mısal. x2 + ( y − 2)2 =1 sheńberdi Ox kósheri átirapında aylandırıwdan
payda bolǵan aylanba bettiń (tordıń) maydanın tabıń.
171

◄ Sheńberdiń teńlemesin tómendegishe
x = (t) = cost
(0 t 2 )
y = (t) = 2 + sin t
parametrlik kóriniste jazamız.
Izlenip atırǵan aylanba bettiń maydanı, (5) formulaǵa muwapıq
2
(П) = 2 (2 + sin t)
 (cost) 2 + (2 + sin t) 2 dt =
(cost) 2 + (2 + sin t) 2 dt =
0
2
= 2 (2 + sin t)dt = 8 2
0
boladı. ►
Anıq integraldıń mexanika hám fizikaǵa qollanıwları.
1. Inerciya momenti. Mexanikada materiallıq tochka háreketi áhmiyetli túsiniklerinin biri esaplanadı.
Ádette, ólshemi jeterli dárejede kishi hám massaǵa iye bolǵan dene materiallıq tochka dep qaraladı.
Meyli tegislikte m massaǵa iye bolǵan A materiallıq tochka berilgen bolıp , bul tochkadan bazı bir l kósherine shekem (yamasa O tochkaǵa shekem) bolǵan aralıq r qa teń bolsın.
Bul
J = mr 2
muǵdar A materiallıq tochkanıń l kósherge (O tochkaǵa) salıstırǵanda inerciya momenti delinedi.
Máselen, A = A(x, y) materiallıq tochkanıń koordinata kósherlerine hám koordinata basına salıstırǵanda inerciya momentleri sáykes tárizde
J x = my 2 , J y = mx 2 , J 0 = m
 x 2 + y 2 boladı. Tegislikte, hár biri sáykes tárizde m0 , m1 , m2 ,....,mn−1
x 2 + y 2 boladı. Tegislikte, hár biri sáykes tárizde m0 , m1 , m2 ,....,mn−1
massaǵa iye bolǵan materiallıq tochkalar sisteması
{A0 , A1 , A2 ,...., An−1}
nıń bazıbir l kósherine (O tochkaǵa) salıstırǵanda inerciya momenti bul
172




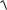
 1
1