
Matematikaliq analiz oqiw qollanba
.pdf
|
|
|
|
n |
2880n4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
boladı. Demek, |
|
|
|
|
|
|
|
|
|
||
b |
b |
|
b − a |
|
|
|
|
|
|
|
|
f (x)dx = |
[ f (x0 ) + f (x2n ) + 4( f (x1 ) + f (x3 ) + ... + f (x2n−1 )) + |
||||||||||
|
|||||||||||
a |
|
6n |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
+ 2( f (x2 ) + f (x4 ) + ... + f (x2n−2 ))] − |
(b − a)5 |
f (iv) ( ). |
|
||||||||
|
|
|
|
|
|
2880n4 |
|
||||
f (x)dx b |
− a [ f (x0 ) + f (x2n ) + 4( f (x1 ) + f (x3 ) + ... |
|
|||||||||
a |
6n |
|
|
|
|
|
|
||||
|
... + f (x2n−1)) + 2( f (x2 ) + f (x4 ) + ... + f (x2n−2 ))]. |
(4 ) |
|||||||||
(4) formula Simpson formulası delinedi. |
|
|
|
|
|
||||||
Bul juwıq formulanıń qáteligi R , |
f (x) funkciya [a,b] da úzliksiz |
f (iv) (x) |
|||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
tuwındıǵa iye bolıw shártinde, |
|
|
|
|
|
|
|||||
|
|
|
R = − (b − a)5 |
f (iv) ( ) |
( (a,b)) |
|
|||||
1
Mısal. е−x2 dx integral durıs tórtmúyeshlikler, trapeciyalar hám Simpson
0
formulaları járdeminde juwıq esaplań.
◄ [0,1] segmentti 5 ta teń bólekke bólemiz. Bunda bóliniw tochkaları x0 = 0, x1 = 0,2, x2 = 0,4, x3 = 0,6, x4 = 0,8, x5 =1,0
bolıp, bul tochkalarda f (x) = e−x2 funkciyanıń mánisleri tómendegishe boladı:
f (x0 ) = 1, 00000, f (x1 ) = 0, 96079, f (x2 ) = 0,85214,
f (x3 ) = 0, 69768, f (x4 ) = 0,52729, f (x5 ) = 0, 36788.
Hár bir bólektiń ortasın ańlatıwshı tochkalar
x1 |
= 0,1 , |
x3 |
= 0,3 , |
x5 |
= 0,5 , |
x7 |
= 0,7 , |
x9 |
= 0,9 |
|||||
|
2 |
|
|
2 |
|
|
2 |
|
|
2 |
|
|
2 |
|
bolıp, bul tochkalardaǵı funkciyanıń mánisleri tómendegishe boladı:
160

f (x1 ) = 0,99005 |
, |
||
|
|
|
|
2 |
|
|
|
f (x3 ) = 0,91393 |
, |
||
|
|
|
|
2 |
|
|
|
f (x5 ) = 0,77680 |
, |
||
|
|
|
|
2 |
|
|
|
f (x7 ) = 0,61263 |
, |
||
|
|
|
|
5 |
|
|
|
f (x9 ) = 0,44486 .
5
a) Durıs tórtmúyeshlikler formulası boyınsha
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
e−x2 dx |
(0,99005 + 0,91393 + 0,77680 + |
|||||||||||
5 |
||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
+ 0,61263 + 0,44486) = |
1 |
3,74027 0,74805 |
||||||||||
5 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||
bolıp, |
|
|
|
|
|
|
|
|
|
|
||
|
R |
|
|
1 |
|
= |
|
|
1 |
0,003 |
||
|
|
|
|
|||||||||
|
|
|
|
|
|
|
||||||
|
|
n |
|
|
12 25 |
|
300 |
|||||
|
|
|
|
|
|
|||||||
boladı.
b) Trapeciyalar formulası boyınsha
1 |
1 |
|
1,00000 + 0,36788 |
|
|
e−x2 dx |
( |
+ 0,96079 + 0,85214 + |
|||
|
|
||||
0 |
5 |
2 |
|
||
|
|
|
|
||
+0,69768 + 0,52729) = 15 (0,68394 + 3,03790) =
=15 3,72184 0,74437
bolıp,
R |
|
|
|
1 |
|
= |
1 |
0,006 |
|
|
|||||||
|
|
|
|
|
||||
n |
|
6 |
25 |
150 |
||||
|
|
|||||||
boladı.
v) Simpson formulası boyınsha
1 |
1 |
|
|
e−x2 dx |
[(1,00000 + 0,36788) + 4(0,99005 + |
||
30 |
|||
0 |
|
||
|
|
+ 0,91393 + 0,77680 + 0,61263 + 0,44486) + 2(0,96079 +
161

+0,85214 + 0,69768 + 0,52729)] = 301 (1,36788 + 4 3,74027) +
+2 3,03790) = 301 (1,36788 + 6,07580 + 14,96108) 0,74682
bolıp,
R |
|
|
12 |
= 0,7 |
10−5 |
|
|
||||||
|
|
|
||||
|
|
|
||||
n |
|
|
2880 |
54 |
|
|
|
|
|
|
|
||
boladı.
9.5. Anıq integraldıń geometriyaǵa, fizikaǵa hám mexanikaǵa
qollanılıwları
Iymek sızıqlı trapeciyanıń maydanın esaplaw.
Meyli f (x) C[a, b] bolıp, x [a,b] da f (x) 0 bolsın.
Joqarıda f (x) funkciya grafigi, qaptal táreplerden x = a , x = b vertikal sızıqlar hám tómennen abcissa kósheri menen shegaralanǵan Q figuranı qarayıq. (10sızılma)
10sızılma
Ádette, bul figura iymek sızıqlı trapeciya delinedi. [a,b] segmentti qálegen
P = {x0 , x1 , x2 ,..., xn } (a = x0 x1 x2 ... xn = b) bóleklewdi alamız. Bul bóleklewdiń hár bir [xk , xk +1 ] aralıǵında
inf{ f (x)} = mk , sup{ f (x)} = M k (k = 0,1,2,..., n −1)
payda boladı.
162
Endi tiykarı xk = xk +1 − xk , biyikligi mk bolǵan (k = 0,1,2,..., n −1) durıs tórtmúyeshliklerdiń birikpelerin payda tapqan durıs kópmúyeshlikti A deyik.
Sonday-aq, tiykarı xk = xk +1 − xk , biyikligi M k bolǵan (k = 0,1,2,..., n −1) durıs tórtmúyeshliklerdiń birikpelerinen payda bolǵan durıs kópmúyeshlikti B dep alayıq. Bunnan,
A Q , |
Q B |
bolıp, olardıń maydanları |
|
n−1 |
n−1 |
( A) = mk xk , |
(B) = M k xk |
k =0 |
k =0 |
boladı. Bul qosındılardı f (x) funkciyanıń [a,b] segmentiniń P bóleklewine
salıstırǵanda Darbudıń tómeni hám joqarı qosındıları ekenligin anıqlaw qıyın emes:
( A) = s( f ; P) , |
(B) = S( f ; P). |
f (x) C[a, b] bolǵanı ushın f (x) funkciya |
[a,b] da integrallanıwshı boladı. |
Onda integrallanıwshılıq kriteriysına muwapıq, 0 alınǵanda hám [a,b] segmenttiń sonday P bóleklewi tabılǵanda,
S( f ; P) − s( f ; P)
boladı. Sebebi, bul
(B) − ( A)
teńsizlik orınlanadı. Bul bolsa, onda 1-teoremaǵa sáykes, qaralıp atırǵan iyrek sızıqlı trapeciyanıń maydanına iye bolıwın bildiredi. Onda anıqlamaǵa sáykes
sup{ ( A)} = inf{ (B)}
boladı. Usı waqıtta,
b |
|
b |
sup{ ( A)} = f ( x)dx, |
inf{ (B)} = f (x)dx |
|
a |
|
a |
bolǵanlıǵı sebepli Q iymek sızıqlı trapeciyanıń maydanı |
|
|
b |
|
|
(Q) = f (x)dx |
(1) |
|
a
163
ǵa teń boladı.
1-mısal. Tegislikte
|
x2 |
+ |
y 2 |
= 1 |
||||
|
a2 |
b2 |
||||||
|
|
|
|
|
||||
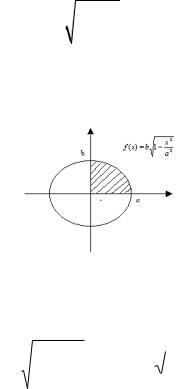
ellips penen shegaralanǵan Q figuranıń maydanın tabıń. |
||||||||
◄Ellips penen shegaralanǵan |
Q |
|
figuranıń maydanı OX hám OY |
|||||
koordinata kósherleri hám |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) = b |
1 − |
x2 |
|
, 0 x a |
||||
a2 |
|
|
||||||
sızıqlar menen shegaralanǵan iymek sızıqlı trapeciya maydanınıń 1/4 ne teń boladı. (11-sızılma ).
11-sızılma
Onda (1) formuladan paydalanıp tómendegini tabamız
|
|
|
a |
|
x |
2 |
|
|
4b |
a |
|
|
|
|
|
|
|
|
|||||||||
(Q) = 4 b 1 − |
|
dx = |
a 2 − x 2 dx = |
||||||||||
a |
2 |
|
a |
||||||||||
0 |
|
|
|
|
|
0 |
|
|
|||||
|
x = a sin t , |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||
= |
|
|
|
0 t |
|
|
= |
|
|
|
|||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
dx = a cos tdt , |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
4b |
a 2 |
2 cos2 tdt = 4ab |
= ab .► |
||||||||
|
|
||||||||||||
|
|
a |
0 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
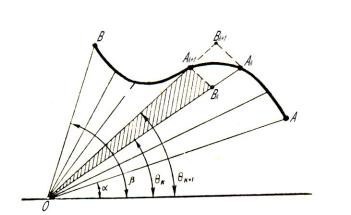
Iymek sızıqlı sektordıń maydanın esaplaw. Meyli AB iymek sızıq polyar koordinatalar sistemasında bul
= ( ) , |
|
( R , R) |
teńleme menen berilgen bolsın. Bunda
164
|
( ) C[ , ] , |
[ , ] да |
( ) 0 . |
|
|
|
|
Tegislikte |
AB iymek sızıq hám OA hám OB |
radius-vektorlar menen |
|
shegaralanǵan Q figuranı qaraymız. |
(12 -sızılma). |
|
|
12sızılma
[ , ] segmentti qálegen
P ={ 0 , 1,..., n } ( = 0 1 ... n = )
bóleklewdi alamız. O tochkadan hár bir polyar múyeshi k ga sáykes OAk radiusvektor ótkizemiz. Nátiyjede OAB -iymek sızıqlı sektor
OAk Ak +1 (k = 0,1,2,...,n −1 ; |
A0 = A , An = B) |
iymek sızıqlı sektorlarǵa ajıraladı. |
|
Bunnan, = ( ) C[ , ] |
|
bolǵanlıǵı ushın [ k , k +1 ] da (k = 0,1,2,..., n −1) |
|
mk = inf{ ( )} , M k |
= sup{ ( )} |
ler bar boladı.
Endi hár bir [ k , k +1 ] segment ushın radius-vektorları sáykes tárizde mk hám M k bolǵan dóngelek sektorlardı payda etemiz. Bunday dóngelek sektorlar maydanǵa iye bolıp, olardıń maydanı sáykes tárizde
|
1 |
mk2 |
k |
, |
1 |
M k2 |
k |
( k = k +1 − k ) |
|
2 |
2 |
||||||||
|
|
|
|
|
|
||||
boladı. Radius-vektorları mk |
(k = 0,1,2,...,n −1) |
bolǵan barlıq dóngelek sektorlar |
|||||||
birikpesinen payda bolǵan figuranı Q1 desek, onda Q1 Q bolıp, onıń maydanı
165

|
1 n−1 |
|
|
|
(Q1 ) = |
|
mk2 |
k |
(3) |
|
||||
|
2 k =0 |
|
|
|
boladı. |
|
|
|
|
Sonıń menen birge, radius-vektorları M k (k = 0,1,2,..., n −1) |
bolǵan barlıq |
|||
dóngelek sektorlar birikpesinen payda bolǵan figuranı Q2 |
desek, onda Q Q2 |
|||||||||||
bolıp, onıń maydanı |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
1 n−1 |
|
|
|
||
|
|
|
(Q2 ) = |
|
M k2 k |
(4) |
||||||
|
|
|
|
|||||||||
|
|
|
|
|
|
|
2 k =0 |
|
|
|
||
boladı. (3) hám (4) qosındılar |
1 |
2 |
( ) funkciyanıń Darbu qosındıları boladı. Bul |
|||||||||
2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||
jaǵdayda, |
1 |
2 ( ) funkciya [ , ] |
da úzliksiz bolǵanı ushın ol integrallanıwshı |
|||||||||
|
||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
||
boladı. Demek, 0 alınǵanda hám [ , ] |
segmenttiń sonday P bóleklewi |
|||||||||||
tabılǵanda, |
|
|
|
|
|
|
|
|
|
|||
|
|
S( |
1 |
2 |
( ); P) − s( |
1 |
2 ( ); P) |
|
||||
|
|
2 |
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||
boladı. Sebebi, bul
(Q2 ) − (Q1 )
teńsizlik orınlanadı. Bul bolsa, onda2-teoremaǵa muwapıq, qaralıp atırǵan iymek sızıqlı sektordıń maydanına iye bolıwın bildiredi. Onda anıqlamasına muwapıq
sup (Q1 ) = inf (Q2 )
boladı. Házirgi waqıtta,
sup (Q1 ) = 2 ( )d ,
inf (Q2 ) = 2 ( )d
bolǵanı sebepli Q iymek sızıqlı sektordıń maydanı
(Q) = 1 2 ( )d 2
ga teń boladı.
166

Doǵanıń uzınlıǵı hám onı esaplaw.
y = f (x) teńleme menen berilgen iymek sızıq uzınlıǵın esaplaw. Meyli |
|
||
AB |
|||
iymek sızıq |
|
|
|
y = f ( x), a x b |
|
|
|
teńleme menen berilgen bolsın. Bunda |
f (x) funkciya [a,b] |
segmentte úzliksiz |
|
hám úzliksiz f (x) tuwındıǵa iye. [a,b] segmenttiń qálegen |
|
|
|
P = {x0 , x1,..., xn } |
(a = x0 x1 ... xn |
= b) |
|
bóleklewin alıp, oǵan sáykes AB doǵaǵa sızılǵan l sınıq sızıqtı payda etemiz. Bul sınıq sızıqtıń perimetri
n−1 |
|
|
|
|
− xk )2 |
+ [ f (xk +1 ) − f (xk )]2 |
|
(l) = (xk +1 |
|||
k =0 |
|
|
|
boladı. Hár bir [xk , xk+1 ] segmentte f (x) funkciyaǵa Lagranj teoremasın qollap
|
n−1 |
|
|
|
|
|
|
|
|
|
− xk )2 +[ f ( k ) (xk +1 − xk )]2 = |
||||||||
(l) = (xk +1 |
|||||||||
|
k =0 |
|
|
|
|
|
|
|
|
n−1 |
|
|
|
|
n−1 |
|
|
||
|
|
|
|||||||
= 1+ f 2 ( k ) (xk +1 − xk ) = 1+ f 2 ( k ) xk , |
|||||||||
k =0 |
|
|
|
k =0 |
|||||
Bunda k [xk , xr+1 ]. |
|
|
|
|
|
|
|
||
|
|
|
|
|
|||||
Bul teńliktegi qosındınıń |
|
1 + f 2 (x) funkciyanıń integral qosındısınan |
|||||||
parqı sonda, integral qosındıda k [xk , xk +1 ] tochka qálegen jaǵdayda joqarıdaǵı qosındıdıda bolsa k tochka Lagranj teoremasına muwapıq alınǵan tayın tochka boladı. Biraq 
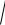 1 + f 2 (x) funkciya integrallanıwshı bolǵanlıǵı sebepli k = k dep alınıwı múmkin. Nátiyjede
1 + f 2 (x) funkciya integrallanıwshı bolǵanlıǵı sebepli k = k dep alınıwı múmkin. Nátiyjede
n−1
(l) = 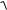 1+ f 2 ( k ) xk
1+ f 2 ( k ) xk
k =0
bolıp, onnan
|
|
n−1 |
|
b |
|
|
|
|
|
|
|
||
lim (l) = lim |
|
1+ f 2 ( k ) xk = |
1+ f 2 (x)dx |
|||
p →0 |
p →0 |
k =0 |
|
a |
|
|
|
|
|
|
|
||
kelip shıǵadı.
Demek, AB doǵanıń uzınlıǵı
167
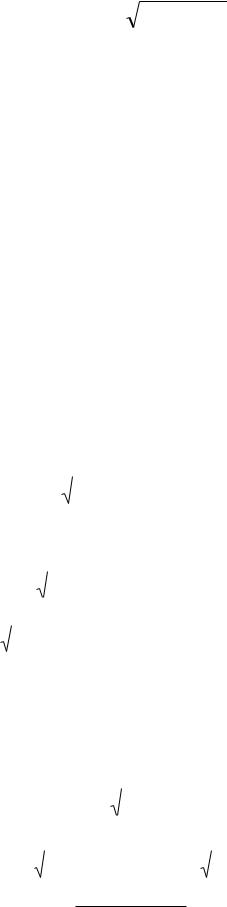
|
b |
|
|
|
|
|
|
( AB) = |
1 + f 2 (x)dx |
(2) |
|
a
boladı. Bul formula járdeminde doǵa uzınlıǵı esaplanadı.
Parametrlik kóriniste berilgen iymek sızıq uzınlıǵın esaplaw.
Meyli, AB iymek sızıq bul
x = (t), |
( t ) |
|
|
y = (t) |
|
teńlemeler sisteması menen berilgen bolıp, (1) shártlerdiń orınlanıwı menen birge
(t), (t) funkciyaları [ , ] |
da úzliksiz (t) hám (t) tuwındılarǵa iye bolsın. |
||||||
[ , ] segmenttiń qálegen |
|
|
|
|
|
|
|
|
P = t0 ,t1,...,tn |
( = t0 |
t1 ... tn |
= ) |
|||
bóleklewdi |
alıp, olarǵa |
|
sáykes |
|
doǵanıń |
|
|
|
AB |
Ak = Ak (xk , yk ) |
|||||
(xk = (tk ) , |
yk = (tk )) tochkaların |
bir-biri menen tuwrı sızıq kesilispesi |
|||||
járdeminde birlestiriwden payda bolǵan l |
sınıq sızıq perimetri |
|
|
||||
|
n−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(l) = [ (tk +1 ) − (tk )]2 +[ (tk +1 ) − (tk ))]2 |
||||||
|
k =0 |
|
|
|
|
|
|
ni qaraymız. Lagranj teoremasınan paydalanıp tabamız:
|
n−1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||
(l) = |
|
2 ( k ) (tk +1 − tk )2 + 2 ( k ) (tk +1 − tk )2 = |
|
||||||||||
|
k =0 |
|
|
|
|
|
|
||||||
n−1 |
|
|
|
|
|
|
|
|
( tk = tk +1 − tk ) |
|
|||
|
|
|
|
|
|
|
|
|
|||||
= 2 ( k ) + 2 ( k ) tk |
|
|
|||||||||||
k =0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Bunda |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k [tk ,tk+1 ]. |
k [tk ,tk +1 ]. |
|
|||||||
keyingi teńlikti tómendegishe jazıp alamız: |
|
|
|
|
|
|
|||||||
|
|
|
|
n−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
(l) = 2 ( k ) |
+ 2 ( k ) tk + |
|
|||||||||
|
|
|
|
k =0 |
|
|
|
|
|
|
|||
n−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 ( k ) + 2 ( k ) |
− 2 ( k ) + 2 ( k )] tk |
|
|||||||||||
+ [ |
(*) |
||||||||||||
k =0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Bunda k [tk ,tk +1 ]. Cebebi 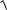
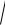 2 (t) + 2 (t) C[ , ] bolsa, onda
2 (t) + 2 (t) C[ , ] bolsa, onda
168
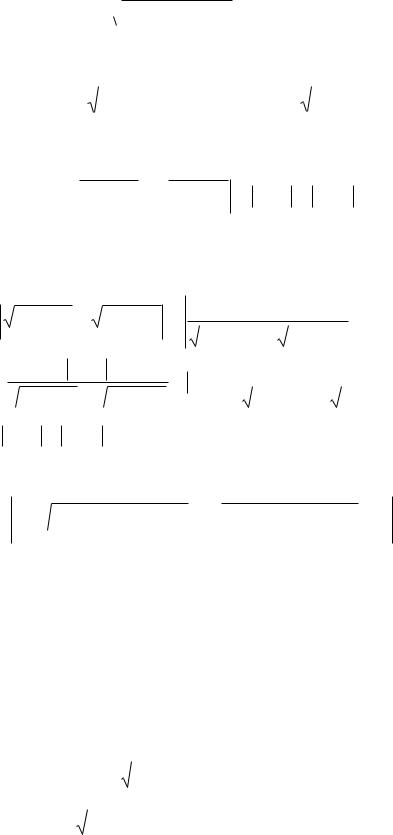

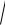 2 (t) + 2 (t) R[ , ]
2 (t) + 2 (t) R[ , ]
bolıp,
|
|
n−1 |
|
|
|
|
|
|
|
|
2 ( k ) + 2 ( k ) tk |
2 (t) + 2 (t)dt |
(3) |
||||
lim |
|
= |
||||||
p |
→0 |
k =0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
boladı. Qálegen a , b , |
c , d haqıyqıy sanlar ushın bul |
|
|
|
||||


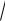 a 2 + b 2 −
a 2 + b 2 − 
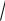 c 2 + d 2 a − c + b − d
c 2 + d 2 a − c + b − d
teńsizlik orınlı boladı. ◄ Haqıyqattan
|
a 2 + b2 − c2 + d 2 = |
|
|
a + c |
+ |
|
||
 a 2 + b2 +
a 2 + b2 +  c2 + d 2
c2 + d 2
a − c + b − d . ►
Bul teńsizlikten paydalanıp
n−1
[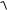 2 ( k ) + 2 ( k )
2 ( k ) + 2 ( k )
k =0
(a 2 − c2 ) + (b2 − d 2 ) |
|
|
|
a − c |
|
|
||||||||||||
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
a 2 + b2 + c2 + d 2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||
b − d |
|
|
|
|
|
|
b + d |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
a 2 + b2 + c2 + d 2 |
|||||||||||||
− 
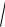 2 ( k ) + 2 ( k )] tk
2 ( k ) + 2 ( k )] tk
n−1 |
|
|
|
|
|
|
n−1 |
|
|
|
|
||||
|
( k ) − ( k ) |
tk + |
|
( k ) − ( k ) |
tk |
||||||||||
k =0 |
|
|
|
|
|
|
k =0 |
|
|
|
|
||||
|
|
|
n−1 |
|
|
|
|
|
|
n−1 |
|
|
|
|
|
|
|
k ( ) t + k ( ) t. |
|||||||||||||
|
|
|
k =0 |
|
|
|
|
|
|
k =0 |
|
|
|
|
|
|
(t) R[ , ], |
|
|
(t) R[ , ] |
|||||||||||
bolǵanlıǵı sebepli |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
n−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 ( k ) + 2 ( k ) − |
||||||||||||
|
lim |
[ |
|||||||||||||
|
p →0 |
k =0 |
|
|
|
|
|
|
|
|
|
(4) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
− 2 ( |
k |
) + 2 ( |
k |
)] t |
k |
= 0 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
boladı. (3) hám (4) qatnaslardı itibarǵa alıp, p → 0 da (*) teńlikte limitke ótsek,
onda AB doǵanıń uzınlıǵı ushın
169
