Добавил:

aysultan Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Каракалпакский государственный университет им. Бердаха

Предмет:

Дискретная математика

Файл:

Matematikaliq analiz oqiw qollanba

.pdf

Скачиваний:

Добавлен:

10.08.2024

Размер:

7.89 Mб

Скачать

☆

<<< < Предыдущая 2 3 4 5 6 7 8 9 10 11 12 1314 / 3614 15 16 17 18 19 20 21 22 23 24 25 26 > Следующая >>>

2. Bóleklep integrallaw usılı. Meyli u(x) hám v(x) funkciyalar úzliksiz

u (x) , v (x) tuwındılarǵa iye bolsın. Bunnan

(u(x) v(x)) = u (x) v(x) + u(x) v (x)
boladı. Demek, F (x) = u(x) v(x) funkciya	f (x) = u (x) v(x) + u(x) v (x)
funkciyanıń dáslepki funkciyası boladı. Bunnan

u (x) v(x) + u(x) v (x) dx = u(x) v(x) + C
kelip shıǵadı. Anıq emes integraldıń 3)- hám 4)- tuwındılarınan paydalanıp
u(x) v (x)dx =u(x) v(x) − u (x) v(x)dx		(5)

kelip shıǵadı. (5) formulanı

u(x) dv(x) =u(x) v(x) − v(x)du(x)

hám jazıw múmkin. Bul (5) formula bóleklep integrallaw formulası delinedi. Onıń járdeminde u(x) v (x)dx integraldı esaplaw u (x) v(x)dx integraldı esaplawǵa keltiriledi.

5-mısal. x cos xdx integralın esaplań.

◄Bóleklep integrallaw formulasınan paydalanıp tabamız:

x cos xdx =	u = x ,	du = dx	= x sin x − sin xdx =
x cos xdx =	u = x ,	du = dx	= x sin x − sin xdx =
	cos xdx = dv	v = sin x

= x sin x + cos x + C. ►

6- mısal. J = x2 + adx integralın esaplań.

◄ Qaralıp atırǵan integralda u =		x2 + a ,		dv = dx bolsa, onda
du =	x		dx ,	v = x

x2 + a

boladı. Bóleklep integrallaw formulasınan paydalanıp tabamız:

+ a −

dx =

J = x x2 + a −

dx = x x2 + a −

+ a

130

= x x 2 + a −

x 2 + a dx + a

+ a

= x x 2 + a − J + a

+ a

Demek,

J = x x2 + a − J + a

+ a

J =

x x2

+ a + a

x2 + a

Bunnan

= ln

x + x2

+ a

+ C .

+ a

Nátiyjede

J = x2 + a dx = 2x x2 + a + a2 ln x + x2 + a + C

kelip shıǵadı. ►

7-mısal. J n =		dx	(n N, a R, a 0)		integraldı esaplań.

	(x2	+ a2 )n
	(x2	+ a2 )n
◄ Bul integralda
		u =	1	, dv = dx

			(x2 + a2 )n

dep alsaq, onda

du = −	2nxdx	, v = x
	(x2 + a2 )n+1

boladı. (5) formuladan paydalanıp tabamız:

J n =

+ 2n

dx =

(x2 + a2 )n

(x2 + a2 )n+1

− a 2

+ 2n

+ a

)

+ a

)

+ a

)

n+1

Nátiyjede

131

J n =

+ 2n

J n − 2na2 J n+1

(x2

+ a2 )n

boladı. Bul teńlikten

J n+1

2n −1

J n

(6)

2na2 (x2 + a2 )n

2n a2

kelip shıǵadı. ►

Ádette, (6) qatnas rekkurent formula delinedi.

Bunnan, n =1 bolǵanda

d (

)

J1 =

arctg

+ C

x2 + a2

1 + (

)

boladı. n 2 bolǵanda sáykes J n

integrallar (6) rekkurent formula járdeminde

tabıladı. Máselen,

J 2 =

arctg

+ C

(x2

+ a2 ) 2

2a2 x2 + a2

2a2

2a2 (x2 + a2 ) 2a3

boladı. ►

8.4. Racional funkciyalardı integrallaw

Meyli f (x) racional funkciya bolıp, onıń integralın esaplaw talap etilsin. Meyli f (x) pútin racional funkciya

f (x) = a0 + a1 x + a2 x2 +... + an xn

bolsın. Onda

f (x) dx = (a0	+ a1 x + a2 x2 +... + an xn ) dx = a0 x + a1	x2	+ a2	x3	+... + an	xn	+ C
		2		3		n

boladı. Meyli f (x) bólshek racional funkciya

+ a x + a

x 2

+ ... + a

x n

P (x)

f (x) =

+ b x + b x 2

+ ... + b x m

(x)

(n N ,

m N )

132

bolsın. Eger n m bolsa, onda Pn (x) kópaǵzanıń Qm (x) kópaǵzalıǵa bóliw

menen f (x) = Pn (x) tiń pútin bólegin ajıratıp, pútin racional funkciya hám durıs

Qm (x)

bólshek jıyındısı kórinisinde ańlatıp alınadı:

f (x) =

Bunnan

f (x)dx

Pn (x)

Qm (x)

= R(

−

= R(x) + Pn (x) . Qm (x)

−

x)dx + Pn (x) dx . Qm (x)


Demek, f (x) =				Pn (x)			(n m) racional funkciyanı integrallaw durıs
Demek, f (x) =				Qm (x)			(n m) racional funkciyanı integrallaw durıs
				Qm (x)
bólshekti integrallawǵa keledi.
1-mısal.			3x2 + 8				dx integraldı esaplań.
1-mısal.	x	3	+ 4x		2	+ 4x	dx integraldı esaplań.
	x		+ 4x			+ 4x

◄ Integral astındaǵı racional funkciyanı ápiwayı bólsheklerge jayamız:

3x2 + 8

−

2)2

x3 + 4x2 + 4x

x x

+ 2

(x +

Demek,

3x2 + 8

dx = 2

−10

x + 2

(x + 2)

+ C.►

= 2ln

+ ln

x + 2

x +

+ 2x4 + 2x2 −1

2-mısal.

dx integralın esaplań.

x(x

+1)

◄ Integral astındaǵı funkciya racional funkciya bolıp, ol durıs emes bólshek boladı. Bul bólshekte x6 + 2x4 + 2x2 −1 kópaǵzalını bólimi x(x2 +1)2 kópaǵzalıǵa bólip, onıń pútin bólegin ajıratamiz:

133

х6 + 2х 4 + 2х 2 −1

х5 + 2х3 + х

х6 + 2х 4 + х 2

х 2 −1

Demek,

x6 + 2x4 + 2x2 −1

= x +

x2 −1

x(x2 +1)2

Endi

x2 −1

durıs bólshekti ápiwayı bólshekke jayamız:

x(x2 +1)2

x2 −1

Bx + C

Dx + E

x(x2 +1)2

2 +1

(x2 +1)2

x2 −1 = A(x2 +1)2 + (Bx + C) x(x2 +1) + (Dx + E) x =

= ( A + B)x4 + Cx3 + (2A + B + D)x2 + (C + E)x + A.

Keyingi teńlikten

A = −1, B =1,

C = 0,

D = 2, E = 0 .

Demek,

x2 −1

−1

x(x2 +1)2

x2 +1

(x2 +1)

Nátiyjede,

x6 + 2x4 + 2x2 −1

= x

−

x(x2 +1)2

x2 +1

(x2 +1)2

bolıp,

x6 + 2x4

+ 2x2 −1

xdx −

dx +

x(x2

+1)

d (x 2 +1)

dx =

− ln

+1)

x 2

− ln

ln(x 2

+1) −

+ C

2 +1

boladı. ►

134

8.5. Trigonometriyalıq funkciyalardı integrallaw

Meyli R(u, v) eki ózgeriwshiniń racional funkciyası bolsın.

R(sin x, cos x) dx

(1)

integraldı qaraymız. Bul integralda

t = tg

almastırıwdı orınlaymız. Onda

2tg

− tg

2 x

1 − t

sin x =

cos x =

2 x

+ t 2

2 x

1 + t 2

1 + tg

+ tg

x = 2arctg t,

dx =

2 dt

1 + t 2

bolsa, onda

1 − t 2

2 ,

2 dt

R(sin x, cos x) dx = 2 R

+ t

1 + t

boladı. Bunnan,

1 − t

+ t

1 + t

ańlatpa t nıń racional funkciyası boladı.

Demek, (1) integraldı esaplaw t = tg

almastırıw menen racional

funkciyanı integrallawǵa keledi.

1-mısal. 1+dxsin x integraldı esaplań.

◄ Bul integralda t = tg 2x almastırıwdı orınlap tabamız:

2dt

1+ t 2

= 2

= −

+ C. ►

+ sin x

+ t)

1+ t

1+ tg

1+ t 2

Ayırım jaǵdaylarda t = cos x,

t = sin x, t = tgx almastırıwlar qolay boladı.

Meyli R(u, v) racional funkciya ushın R(−u, v) = −R(u, v)

bolsın. Onda

135

R(sin x, cos x) dx = R2 (sin2 x, cos x)sin x dx =

t= cos x

=dt = −sin xdx = − R2 (1− t 2 ,t) dt

boladı. Meyli R(u, v) racional funkciya ushın R(u,−v) = −R(u, v) bolsın. Onda

R(sin x, cos x) dx = R3 (sin x, cos2 x) cos x dx =

t= sin x

=dt = cos xdx = R3 (t,1 − t 2 ) dt

boladı. Meyli R(u,v) racional funkciya ushın

R(−u,−v) = R(u, v)

bolsın. Onda

R(sin x, cos x) dx = R2 (tgx, cos2 x) dx =

t = tgx

= R2 (t,

)

dx =

1 + t 2

+ t 2

boladı.

2-mısal. sin3 x cos4 xdx integraldı esaplań.

◄ Integral astındaǵı funkciya ushın R(−u, v) = −R(u, v)

boladı. Sonıń ushın

cos x = t delinse, onda − sin xdx = dt bolıp, onda

sin 3 x cos 4 xdx = (t 2 −1)t 4 dt =

t 7

−

t 5

+ C =

cos 7 x −

cos 5 x + C

boladı. ►

8.6. Ayırım irracional funkciyalardı integrallaw

1. R(x , n ax + b )dx kórinisindegi integrallardı esaplaw. cx + d

136

t 2 dt

Meyli R(u, v) eki ózgeriwshiniń racional funkciyası bolıp, a, b, c , d lar

haqıyqıy sanlar, n N bolsın.

R(x, n	ax + b	)dx ,	ad − bc 0,

	cx + d

kórinisindegi integrallardı qaraymız. Bul integral ózgeriwshini almastırıw járdeminde racional funkciyanıń integralına keledi:

ax + b

= t, x

b − t n d

R(x, n

ax + b

)dx =

cx + d

ct n − a

cx + d

dx =

(ad − bc)n

n−1

(a − ct n )2

dt n − b

(ad − bc)nt n−1

dt .

= R

− ct

, t

(a − ct

)

1-mısal. 11 +− xx 1 −1 x dx integraldı esaplań.

◄Bul integralda t =

1 + x

almastırwın orınlaymız. Onda

1 − x

x =

t 2

−1

dx =

4tdt

t 2

(t 2

+1)2

bolıp,

t 2 dt

1+ x

dx =

1− x

− x

boladı. Bunnan,

t 2 +1 = t − arctgt + C .

Demek,

1 + x

dx = 2

− 2arctg

+ C ►

1 − x

2. R(x ,

)dx kórinisindegi integrallardı esaplaw. Integralda

ax2 + bx + c

a ,b, c -haqıyqıy sanlar bolıp, onda

ax2 + bx + c

kvadrat úshaǵzalıǵa teń

korenlerge iye emes.

137

Qaralıp atırǵan


R(x , ax 2 + bx + с )dx			(1)

integral tómendegi úsh almastırıw járdeminde racional funkciya integrallawǵa keledi.

a) a 0 bolsın. (1) integralda bul

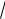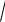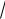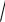t = ax + ax2 + bx + c (yoki t = −ax + ax2 + bx + c )

almasıtırıwın orınlaymız. Onda

ax2 + bx + c = t 2 − 2 a xt + ax2 ,

x =

t 2 − c

, dx =

2( at

2 + bt + c a )

dt ,

at + b)2

at + b

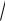ax2 + bx + c = 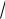at 2 + bt + c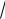a 2at + b

boladı. Nátiyjede

R(x , ax 2 + bx + с )dx =

t 2 − c

a t 2 + bt + c a

2( a t 2 + bt + c a )

= R

2 at + b

2 a t + b

(2 a t + b)

boladı.

2-mısal. x + x2 + x +1 integraldı esaplań.

◄ Integralda t = x + x2 + x +1 almastırıwın orınlaymız. Nátiyjede

x =

t 2

−1

dx = 2

t 2 + t +1

1 + 2t

(1 + 2t)2

bolsa, onda

= 2

t 2 + t +1

(1 + 2t)

x + x 2 + x +1

boladı. Eger

2(t 2 + t +1)

−

t(1 + 2t)2

+ 2t

+ 2t)2

138

esapqa alsaq, onda

+ x 2

+ x +1

−

+ 2t

−

2t)

dt =

= 2 ln

−

ln1 + 2t

+ C =

2(1 +

2t)

ln1 + 2x + 2

= 2 ln

x +

x 2 + x +1

−

x 2 + x +1

+ C

2(1 + 2x + 2 x 2 + x +1)

kelip shıǵadı. ►

b) с 0 bolsın. Bul jaǵdayda (1) integralda

yamasa

t = x ( ax + bx + c −

= x ( ax + bx + c + c )

almasıtırıwın orınlaymız. Onda

x =

2 c t − b

, dx =

ct2 − bt + c a

dt ,

a − t2

(a + t)2

c t 2 − bt + a c

ax2 + bx + c =

a − t 2

bolıp, (1) integral racional funkciyanıń integralına keledi:

R(x ,

= R

ax 2 + bx + c )dx =

2 c t − b

c t 2 − bt + a c

ct 2 − bt + c a

2 ,

a − t

(a + t)

v)ax2 + bx + c kvadrat úshaǵzalını hár qıylı x1 hám x2 haqıyqıy

korenlerge iye bolsın:

	ax2 + bx + c = a(x − x ) (x − x ) .
				1		2
		1
Bul jaǵdayda (1) integralda t =		1		ax2 + bx + c almastırıwdı orınlaymız.
Bul jaǵdayda (1) integralda t =		x − x1		ax2 + bx + c almastırıwdı orınlaymız.
		x − x1
Nátiyjede
	−ax + x t2					a( x − x	)
	−ax + x t2				ax2 + bx + c =	a( x − x	)
x =		2 1	,			1 2		t
x =	t2 − a		,			t2 − a		t
	t2 − a					t2 − a

139

<<< < Предыдущая 2 3 4 5 6 7 8 9 10 11 12 1314 / 3614 15 16 17 18 19 20 21 22 23 24 25 26 > Следующая >>>

Соседние файлы в предмете Дискретная математика

#
10.08.20242.46 Mб6Aniq integrallar.pdf
#
09.08.20243.06 Mб5Apiwayi differencialliq tenlemeler.pdf
#
09.08.20243 Mб7Differencialliq tenlemeler.pdf
#
09.08.20241.38 Mб17Joqari matematika paninen lekciyalar.pdf
#
09.08.20241.17 Mб11Matematika (Lekciya).pdf
#
10.08.20247.89 Mб15Matematikaliq analiz oqiw qollanba.pdf
#
10.08.20244.64 Mб17Matematikaliq analiz.pdf
#
10.08.20246.32 Mб73Matematikani oqitiw metodikasi.pdf
#
10.08.20241.7 Mб4Tenlemeler ham tensizlikler.pdf
#
10.08.20241.65 Mб3Tensizliklerdi dalillew usillari.pdf