
Matematikaliq analiz oqiw qollanba
.pdf
kelip shıǵadı, bunda x → 0 |
da |
→ 0. |
Demek, |
f (x) funkciya |
differenciallanıwshı.► |
|
|
|
|
2-anıqlama. Funkciya ósimindegi f '(x0 ) x ańlatpa f (x) |
funkciyanıń x0 |
|||
tochkadaǵı differencialı delinedi hám |
df (x0 ) |
kórinisinde belgilenedi |
||
df (x0 ) = f '(x0 ) x . |
|
|||
Meyli x (a, b) tochkada differenciallanıwshı |
f (x) funkciyanıń grafigi 6- |
|||
sızılmada súwretlengen iymek sızıqtı ańlatsın: |
|
|
||
6-sızılma
Keltirilgen sızılmadan kórinip turǵanday,
|
|
|
|
DC |
|
= tg |
|
|
|
|
|
|
|
AC |
|
|
|
||
|
|
|
|
|
|
|
|
||
bolıp, DC = tg AC = f (x) x boladı. |
|
|
|
|
|||||
Demek, |
f (x) |
funkciyanıń |
x tochkadaǵı differencialı funkciya grafigine |
||||||
(x, f (x)) tochkada ótkizilgen urınba ósimi |
DC nı ańlatadı. |
|
|
||||||
Meyli |
f (x) = x, x R bolsın. Bul funkciya |
differenciallanıwshı |
bolıp, |
||||||
df (x) = (x) x = x , |
yamasa |
dx = x |
boladı. |
Demek, |
(a, b) |
da |
|||
differenciallanıwshı |
f (x) funkciyanıń differencialın |
|
|
|
|||||
|
|
|
df (x) = f (x) dx |
|
|
|
|||
kóriniste ańlatıw múmkin.
Endi ápywayı funkciyalardıń differencialların keltiremiz:
1. d (x ) = x −1dx, |
(x 0); |
90

2. |
d (a x ) = a x ln a dx, |
(a 0, a 1); |
|
|||||
3. |
d (log |
x) = |
1 |
log |
|
edx, |
(x 0, a 0, |
a 1); |
|
a |
|||||||
|
a |
|
x |
|
|
|
||
|
|
|
|
|
|
|
||
4.d (sin x) = cos xdx ;
5.d (cos x) = −sin xdx ;
6. |
d (tgx) = |
1 |
|
|
|
|
|
dx, |
(x |
+ k , k = 0, 1, ...); |
||||||||||
cos2 |
|
|
|
|
||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
2 |
||||||||||
7. |
d (ctgx) = − |
|
|
1 |
|
|
|
dx, |
|
|
(x k , k = 0, 1, ...); |
|||||||||
sin2 x |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
8. |
d (arcsinx) = |
|
1 |
|
|
|
|
|
dx, |
(−1 x 1); |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1 − x2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
9. |
d (arccosx) = − |
|
|
|
|
|
1 |
|
|
|
|
|
dx, |
(−1 x 1); |
||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
1 − x2 |
|
|
|
||||||||
10. |
d (arctgx) = |
1 |
|
|
dx; |
|
||||||||||||||
|
|
|
|
|||||||||||||||||
1 + x2 |
|
|||||||||||||||||||
11. |
d (arcctgx) = − |
|
1 |
|
|
|
|
dx; |
|
|||||||||||
|
+ x2 |
|
|
|||||||||||||||||
|
|
|
|
|
1 |
|
|
|
||||||||||||
12.d (shx) = chxdx ;
13.d (chx) = shxdx ;
14. |
d (thx) = |
1 |
|
dx; |
|||
|
|
|
|||||
|
|
ch2 x |
|
||||
15. |
d(cthx)= − |
|
1 |
dx (x 0) |
|||
sh2 x |
|||||||
|
|
|
|
||||
Meyli f (x) hám g (x) funkciyaları (a, b) da berilgen tochkada differenciallanıwshı bolsın. Onda x (a, b) da
1) d (c f (x)) = cdf (x), c = const ;
2)d ( f (x) + g(x)) = df (x) + dg(x);
3)d ( f (x)g(x)) = g(x)df (x) + f (x)dg(x);
|
|
f (x) |
|
g(x)df (x) − f (x)dg(x) |
|
|||
4) |
d |
|
|
= |
|
|
|
, (g(x) |
|
|
2 |
|
|||||
|
|
|
|
|
g |
(x) |
|
|
|
g(x) |
|
|
|
||||
bolıp, x (a, b)
0).
91
boladı. |
|
|
|
|
|
|
Meyli |
y = f (x) |
funkciya |
X R |
kóplikte, |
g( y) |
funkciya |
Y { f (x) : x X } kóplikte berilgen |
bolıp, f (x) |
hám g ( y) |
tuwındılarǵa iye |
|||
bolsın. Bul jaǵdayda |
|
|
|
|
|
|
|
|
d (g( f (x))) = g'( f (x)) df (x) |
|
|
||
boladı.
◄ Quramalı funkciyanıń tuwındısın esaplaw qaǵıydasınan paydalanıp tabamız:
|
|
|
|
|
d (g( f (x))) = g( f (x)) |
dx = g ( f (x)) f |
(x)dx = g ( f (x)) df (x) .► |
||
Mısal. Anıqlamadan paydalanıp , |
f (x) = x − 3x2 funkciyanıń x0 = 2 |
|||
tochkadaǵı differencialın tabıń.
◄Bul funkciyanıń x0 = 2 tochkadaǵı ósimin tabamız:
f (2) = f (2 + x) − f (2) = 2 + x − 3(2 + x)2 − 2 +12 =
= −11 x − 3 x2 = −11 x + (−3 x) x .
Demek, d f (2) = −11 dx . ►
|
6.4. Juwıq esaplaw formulaları |
Funkciya differencialı járdeminde juwıq formulalarǵa alıp kelinedi. |
|
Meyli f (x) |
funkciya (a, b) da berilgen bolıp, x0 (a, b) tochkada shekli |
f (x0 ) tuwındıǵa |
( f (x0 ) 0) iye bolsın. Onda x → 0 da |
|
f (x0 ) = f (x0 ) x + ( x) |
boladı. Onda f (x) funkciya x0 tochkada differenciallanıwshı bolıp, onıń differencialı
d f (x0 ) = f (x0 ) x boladı. Bunnan f (x0 ) − df (x0 ) = ( x) bolıp, x → 0 da
f (x0 ) − df (x0 ) → 0
x
92
boladı. Nátiyjede
f (x0 ) df (x0 ) ,
yamasa
f (x0 + x) f (x0 ) + f |
(x0 ) x |
(1) |
juwıq formula payda boladı. (1) formula x0 (a, b) |
tochkada differenciallanıwshı |
|
f (x) funkciyanıń x0 tochkadaǵı ósimi f (x0 ) dı onıń |
usı tochkadaǵı |
|
differencialı df (x0 ) menen almastırıw múmkinligin kórsetedi. Bul almastırıwdıń áhmiyeti funkciya ósimi argument ósiminiń, ulıwma aytqanda quramalı funkciyası bolǵan jaǵdayda, funkciya differencialı bolsa argument ósiminiń sızıqlı funkciyası boladı. (1) formulada x = x − x0 bolsa, onda
f (x) f (x0 ) + f (x0 )(x − x0 ) |
(2) |
boladı. |
|
Mısal. Bul sin290 muǵdar juwıq esaplań. |
|
|
|
|
|
|
|
|||
◄ Eger f (x) = sin x, x = 300 bolsa, onda (2) formulaǵa muwapıq |
||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
||
sin 290 sin300 + cos 300 (290 − 300 ) |
= 0,5 − |
3 |
|
|
0,4848 |
|||||
|
|
|
|
|
||||||
|
|
3600 |
|
2 |
3600 |
|
||||
boladı. ► |
|
|
|
|
|
|
|
|
|
|
Bizge málim, |
x0 (a, b) tochkada differenciallanıwshı |
f (x) funkciya |
||||||||
grafigine (x0 , |
f (x0 )) tochkada ótkizilgen urınbanıń teńlemesi tómendegi kóriniste |
|||||||||
jazıladı: |
|
|
|
|
|
|
|
|
|
|
|
|
y = f (x0 ) + f (x0 )(x − x0 ) . |
|
|
|
|
|
|
||
Demek, (2) juwıq formula geometriyalıq kóz-qarastan, f (x) |
funkciya belgilengen |
|||||||||
iymek sızıqtı |
x0 |
tochkanıń jeterli kishi dógereginde |
|
|
funkciya grafigine |
|||||
(x0 , f (x0 )) tochkada ótkizilagen urınba menen almastırılıwı múmkinligin
bildiredi.
(2) formulada x0 = 0 delinse ol usı
f (x) f (0) + f '(0)x |
(3) |
kóriniske keledi.
93

f (x) funkciya sıpatında (1+ x) , 
 1+ x, e x , ln(1 + x), sin x, tgx funkciyalardı alıp, olarǵa (3) formulanı qollaw nátiyjesinde tómendegi juwıq formulalar payda boladı:
1+ x, e x , ln(1 + x), sin x, tgx funkciyalardı alıp, olarǵa (3) formulanı qollaw nátiyjesinde tómendegi juwıq formulalar payda boladı:
(1 + x) 1 + x,

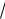 1 + x 1 + 12 x,
1 + x 1 + 12 x,
ex 1+ x , ln(1 + x) x, sin x x, tgx x.
|
|
6.5. Joqarı tártipli tuwındı hám differenciallar |
|
|||||||||||
Meyli |
|
f (x) funkciya (a, b) da berilgen |
bolıp, |
x (a, b) da |
f (x) |
|||||||||
tuwındıǵa iye bolsın. Bul |
f (x) funkciyanı g (x) |
arqalı belgileymiz: |
|
|||||||||||
|
|
|
|
g(x) = f (x) |
(x (a, b)) . |
|
|
|
|
|||||
1-anıqlama. Eger x0 (a, b) tochkada g (x) funkciya g (x0 ) tuwındıǵa iye |
||||||||||||||
bolsa, bul tuwındı f (x) |
funkciyanıń |
x0 |
tochkadaǵı ekinshi tártipli tuwındısı |
|||||||||||
delinedi hám |
f (x0 ) yamasa |
|
d 2 |
f (x0 ) |
kórinisinde belgilenedi. |
|
|
|||||||
|
dx2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Tap usıǵan uqsas, |
f (x) |
tiń 3-tártipli |
|
, 4-tártipli f |
IV |
(x) h.t .b. tártipli |
||||||||
|
f (x) |
|
||||||||||||
tuwındıları anıqlanadı. |
|
|
|
|
|
|
|
|
|
|
|
|
||
Ulıwma, f (x) funkciyanıń n −tártipli tuwındısı f (n) (x) |
tiń tuwındısı f (x) |
|||||||||||||
funkciyanıń (n +1) − tártipli tuwındısı delinedi: |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
f (n+1) (x) = (f (n) (x)) . |
|
|
|
|
|
|||
Ádette, |
f (x) funkciyanıń f (x), |
f (x), ... tuwındıları onıń joqarı tártipli |
||||||||||||
tuwındıları |
delinedi. Sonı aytıp ótiw kerek, |
f (x) |
funkciyanıń x (a, b) da |
|||||||||||
n −tártipli |
tuwındınıń |
barlıǵı |
bul |
funkciyanıń |
usı |
tochka dógereginde |
||||||||
94

1−, 2−, ..., (n −1) −tártipli tuwındıları barlıǵın kórsetedi. Biraq bul tuwındılardıń
n −tártipli tuwındı barlıǵı, ulıwma aytqanda, kelip shıqpaydı. Máselen,
f (x) = x | x | 2
funkciyanıń tuwındısı f '(x) = | x | bolıp, bul funkciya х = 0 tochkada tuwındıǵa
iye emes, yamasa berilgen funkciyanıń |
х = 0 da birinshi tártipli tuwındısı bar, |
|
ekinshi tártipli tuwındısı bolmaydı. |
|
|
1-mısal. f (x) = a x bolsın, a 0, |
x R. Bul funkciya ushın |
|
(a x ) = a x ln a, |
|
|
(a x ) = (a x ln a) = a x (lna)2 , |
|
|
ulıwma |
|
|
(a x )(n) = a x (lna)n |
(1) |
|
boladı. (1) qatnastıń orınlı bolıwı matematikalıq indukciya usılı menen dállilenedi.
2-mısal. f (x) = sin x bolsın. Bul funkciya ushın
|
|
|
|
|
|
|
|
(sin x) = cos x = sin x + |
, |
|
|
|
|||
|
|
|
|
2 |
|
|
|
(sin x) = (cos x) = −sin x = sin x + 2 |
, |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
Ulıwma, |
|
|
|
|
|
|
|
|
(sin x)(n) |
= sin x + n |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
boladı. Usıǵan uqsas, |
|
|
|
|
|
|
|
|
(cos x) |
(n) |
|
|
|
|
|
|
|
= cos x + n |
2 |
|
|
||
|
|
|
|
|
|
|
|
boladı. |
|
|
|
|
|
|
|
3-mısal. f (x) = x |
bolsın, x 0, |
R . Bul funkciya ushın |
|||||
(x ) = x −1 ,
(x ) = ( x −1 ) = ( −1)x −2 ,
95
ulıwma,
|
|
|
|
(x )(n) = ( −1)( − 2)...( − n +1)x −n |
|
|||||||||||||
boladı. Tiykarınan |
f (x) = |
1 |
, |
(x 0) funkciya ushın |
|
|||||||||||||
|
|
|||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
(n) |
= |
(−1)n n! |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xn+1 |
|
||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|||||
bolıp, onnan |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(ln x)(n) = |
(−1)n−1 (n −1)! |
|
|||||||||
|
|
|
|
|
|
|
|
xn |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
kelip shıǵadı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Meyli |
f (x) |
hám g (x) |
funkciyalar (a, b) da berilgen bolıp, x (a, b) da |
|||||||||||||||
f (n) (x) hám g (n) (x) |
tuwındılarǵa iye bolsın. Onda: |
|
||||||||||||||||
1) (c f (x))(n) |
= c f (n) (x), |
c = const ; |
|
|||||||||||||||
2) ( f (x) g(x))(n) = f (n) (x) g(n) (x) ; |
|
|
|
|
||||||||||||||
|
|
|
|
n |
|
|
|
|
|
g(n−k ) (x) |
|
|||||||
3) ( f (x) g(x))(n) = Cnk f (k ) (x) |
(2) |
|||||||||||||||||
|
|
|
|
k =0 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
k |
n(n −1)...(n − k +1) |
|
|
|
(0) |
|
|
|
|
|
|
||||||
Cn = |
|
|
|
|
|
|
, |
|
f |
|
(x) = f (x) |
|
||||||
|
|
k! |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
boladı. Ádette, (2) Leybnic formulası delinedi.
4-mısal. y = x2 cos 2x funkciyanıń n −tártipli tuwındısın tabıń.
◄Leybnic formulasında f (x) = cos2x , |
|
g(x) = x2 |
dep alamız. Onda bul |
|||||||
formulaǵa muwapıq, |
g(x) = x2 funkciya ushın k 2 bolǵanda |
|||||||||
|
g (k ) (x) = (x2 )(k ) = 0, |
(k 2) |
|
|||||||
bolıwın itibarǵa alıp, |
|
|
|
|
|
|
|
|
|
|
(x2 cos 2x)(n) = C0 x2 |
(cos2x)(n) + C1 |
(x2 ) (cos2x)(n−1) |
+ C2 |
(x2 ) (cos2x)(n−2) |
||||||
n |
|
n |
|
|
|
|
|
|
n |
. |
Bunnan, |
|
|
|
|
|
|
|
|
|
|
|
(cos2x) |
(n) |
= 2 |
n |
|
|
|
|
|
|
|
|
|
cos 2x + n |
2 |
, |
|
||||
|
|
|
|
|
|
|
|
|
|
|
96
(cos2x) |
(n−1) = 2n−1 cos |
2x + (n −1) |
|
= 2n−1 sin |
2x + n |
|
, |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
(cos2x)(n−2) |
= 2n−2 cos |
2x + (n − 2) |
|
= −2n−1 cos |
2x + n |
. |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
Demek,
( x2 cos 2x )(n) = 2n |
x2 |
− |
n(n −1) |
cos |
|
2x + n |
|
+ 2n nx sin |
|
2x + n |
. ► |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||
|
|
4 |
|
|
|
2 |
|
|
|
2 |
|
Joqarı tártipli differencialı. Meyli f (x) funkciya (a, b) |
da berilgen bolıp, |
||
x (a, b) |
tochkada f (x) tuwındıǵa iye bolsın. Bunnan, |
f (x) funkciyanıń |
|
differencialı |
|
|
|
|
df (x) = f (x)dx |
|
(3) |
bolıp, bunda dx = x funkciya argumentinıń ıqtıyarlı ósimi boladı. |
|
||
2-anıqlama. f (x) funkciyanıń x (a, b) tochkadaǵı differencialı df (x) |
tiń |
||
differencialı |
f (x) funkciyanıń x (a, b) tochkadaǵı ekinshi tártipli differencialı |
||
delinedi hám |
d 2 f (x) kórinisinde belgilenedi: |
|
|
|
d 2 f (x) = d (df (x)) . |
|
|
Tap usıǵan uqsas f (x) funkciyanıń úshinshi d 3 f (x) , tórtinshi d 4 f (x) |
h. |
||
t.b. tártiptli differencialları anıqlanadı. |
|
|
|
Ulıwma, f (x) funkciyanıń n −tártipli differencialı d n f (x) tiń differencialı f (x) funkciyanıń (n +1) − tártipli differencialı delinedi:
d n+1 f (x) = d (d n f (x)).
5-mısal. f (x) = xe−x funkciyanıń ekinshi tártipli differencialın tabıń.
◄ Berilgen funkciyanıń ekinshi tártipli differencialın anıqlamaǵa muwapıq tabamız:
d 2 f (x) = d(df (x)) = d(d(xe−x )) = d(xde−x + e−x dx) == d(−xe−x dx + e−x dx) =
= −d(xe−x )dx + (de−x )dx = −(xde−x + e−x dx)dx − e−x (dx)2 = xe−x (dx)2 − = x e−x (dx)2 − e−x (dx)2 − e−x (dx)2 = (x − 2)e−x (dx)2 . ►
Differenciallaw qaǵıydasınan paydalanıp tabamız:
97
d2 f (x) = d(df (x)) = d( f (x)dx) = dx d( f (x)) = dx f (x)dx = f (x)(dx)2, |
(4) |
|
d 3 f (x) = d (d 2 f (x)) = |
f (x)(dx)3 , |
|
............................................ |
|
|
d n f (x) = f (n) (x)(dx)n |
|
|
Meyli f (x) hám g (x) funkciyalar (a, b) |
da berilgen bolıp, x (a, b) |
|
tochkada n −tártipli differenciallarǵa iye bolsın. Bul jaǵdayda:
1) d n (c f (x)) = c d n f (x), c = const;
2)d n ( f (x) g(x)) = d n f (x) d n g(x);
3)d n ( f (x) g(x)) = d n f (x) g(x) + Cn1d n−1 f (x) dg(x) +
+... + Cnk d n−k f (x) d k g(x) +... + f (x) d n g(x)
boladı.
6.6. Differenciallıq esaptıń tiykarǵı teoremaları
Tuwındıǵa iye bolǵan funkciyalar haqqındaǵı teoremalar keltirilgen. Bul
teoremalar funkciyalardı tekseriwde áhmiyetli rol oynaydı. |
|
|
|||||
1-teorema |
(Ferma teoreması). Meyli f (x) funkciya X R kóplikte |
||||||
berilgen |
bolsın. |
Onda |
x0 X |
tochkanıń |
dógeregi |
ushın |
|
U (x0 ) = (x0 |
− , |
x0 + ) X |
( 0) bolıp, tómendegi shártler orınlı bolsın: |
||||
1) x U |
(x0 ) da f (x) f (x0 ) |
( f (x) f (x0 )), |
|
|
|||
2) f (x0 ) bar hám shekli bolsın. Onda f (x0 ) = 0 boladı.
◄ Meyli x U (x0 ) da f (x) f (x0 ) bolsın. Bunnan f (x) − f (x0 ) 0
boladı.
Shártke muwapıq f (x) funkciya x0 tochkada shekli f (x0 ) tuwındıǵa iye.
Sonıń ushın
98
f (x |
|
) = lim |
f (x) − f (x0 ) |
= |
lim |
|
f (x) − f (x0 ) |
= |
|
|
lim |
f (x) − f (x0 ) |
|||||||||||||
0 |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
x→x0 |
x − x |
|
|
|
x→x0 +0 |
|
x − x |
|
|
|
|
x→x0 −0 |
x − x |
|
|
||||||||
|
|
|
0 |
|
|
|
0 |
|
|
|
0 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
boladı. Bul jerde, x x0 bolǵanda |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
f (x) − f (x0 ) |
|
0 |
|
lim |
|
f (x) − f (x0 ) |
= f ' (x0 ) 0 , |
|||||||||||||||||
|
|
|
x − x |
|
|
|
|
x − x |
|
|
|
|
|
||||||||||||
|
|
|
0 |
|
|
|
|
|
|
x→x0 |
+0 |
|
0 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x x0 bolǵanda |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) − f (x0 ) |
|
0 |
|
lim |
|
f (x) − f (x0 ) |
= f ' (x0 ) 0 |
|||||||||||||||||
|
|
|
x − x |
|
|
|
|
x − x |
|
|
|
|
|||||||||||||
|
|
|
0 |
|
|
|
|
|
|
x→x0 |
− 0 |
|
0 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
bolıwınan f ' (x0 ) = 0 kelip shıǵadı. ► |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
2-teorema (Roll teoreması). Meyli |
f (x) funkciya [a, b] da berilgen bolıp, |
||||||||||||||||||||||||
tómendegi shártlerin orınlı bolsın |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1)f (x) C[a, b],
2)x (a, b) da f (x) bar hám shekli,
3)f (a) = f (b) bolsın.
Onda sonday x0 (a, b)tochka tabılıp, f (x0 ) = 0 boladı. |
|
|
||||||
◄ Shártke muwapıq |
f (x) C[a, b]. |
Onda |
Veyershtrasstıń ekinshi |
|||||
teoremasına muwapıq f (x) |
funkciya [a, b] |
da óziniń eń úlken hám eń kishi |
||||||
mánislerge erisedi, yamasa sonday с1 , c2 |
tochkalar (c1 , c2 [a, b]) tabılsa, |
|
||||||
|
|
f (c1 ) = max{ f (x) | x [a, b]}, |
|
|
||||
|
|
f (c2 ) = min{ f (x) | x [a, b]} |
|
|
||||
boladı. Eger |
f (c1 ) = f (c2 ) |
bolsa, onda |
[a, b] |
da f (x) = const |
bolıp, |
|||
x0 (a, b) da |
f ' (x0 ) = 0 boladı. |
|
|
|
|
|
||
Eger |
f (c1 ) f (c2 ) bolsa, onda |
f (a) = f (b) |
bolǵanlıǵı sebepli |
f (x) |
||||
funkciya |
f (c1 ) hámde f (c2 ) |
mánisleriniń keminde bir [a, b] segmenttiń ishki |
||||||
x0 (a x0 |
b) tochkasında erisedi. Ferma teoremasına tiykarlanıp |
f (x0 ) = 0 |
||||||
boladı. ► |
|
|
|
|
|
|
|
|
3-teorema (Lagranj teoreması). Meyli |
f (x) funkciya [a, b] |
da berilgen |
||||||
bolıp, tómendegi shártlerin orınlasın:
99
