Matematikani oqitiw metodikasi

Kerekli ólshemlerdi orınlań. Nelerdi sezdińiz? Kópmúyeshliklerdiń perimetrin qolaylı usılda esaplań.

Úshmúyeshliktiń perimetri 174 sm.

a)eger sol úshmúyeshliktiń úsh tárepi ózara teń bolsa, bir tárepiniń uzınlıǵın tabıń;

b)eger sol úshmúyeshliktiń eki tárepi ózara teń hám úshinshi tárepi 56 sm bolsa, qalǵan táreplerin tabıń.

Tárepi 50 sm bolǵan kvadrat kórinisindegi taxtashalardan kub jasamaqshı.

a)bunday taxtashalardan neshewin alıw kerek?

b)bir taxtashanıń maydanın tabıń.

Úshmúyeshliktiń perimetri 40 sm, bir tárepiniń uzınlıǵı 15 sm,

ekinshi tárepi 12 sm bolsa, úshinshi tárepin tabıń.

a)sızılmadan 5 úshmúyeshlikti tawıp

jazıń;

b)sızılmadaǵı tórtmúyeshliklerdiń perimetrin ólshep tabıń.

MAYDANLARDÍ FORMULA JÁRDEMINDE ESAPLAW

Ultanı 5 sm hám biyikligi 3 sm bolǵan tuwrı tórtmúyeshlik sızıń. Onıń qasında ultanı 4 sm hám bálentligi 3 sm bolǵan tuwrı tórtmúyeshlik sızıń. Bul tuwrı tórtmúyeshlikler maydanları qosındısın eki usıl menen esaplań:

Ultanınıń uzınlıǵı 3 sm, biyikligi 4 sm hám ultanınıń uzınlıǵı

5sm, biyikligi 4 sm bolǵan tuwrı tórtmúyeshliklerdi qarama-qarsı

284

sızıń. Olardıń maydanları qosındısın eki usıl menen esaplań. 1- hám 2-máselelerden qanday juwmaqqa keliw múmkin?

Ultanı a, biyikligi b hám ultanı c, biyikligi b bolǵan tuwrı tórtmúyeshlikler qarama-qarsı qoyılǵan. (a+c)b=ab+bc ekenin kórsetiń. Bunıń menen kóbeytiw ámeliniń qosıwǵa qaraǵanda bólistiriw nızamın dálillegen bolasız.

Kesteni toltırıń. Bunda S-tuwrı tórtmúyeshliktiń maydanı, a- ultanı, b-biyikligi. S=a∙b.

a) tárepleri pútin sanlar hám perimetri 12 sm bolǵan tuwrı tórtmúyeshlikler sızıń. Olardıń maydanların esaplań. Sáykes keste dúziń. Qanday kórinis ushın maydanı eń úlken boldı?

□+□=18 bolsa, □∙□ qashan eń úlken boladı?

Tárepleriniń uzınlıǵı pútin sanlar hám perimetri 20 sm bolǵan tuwrı tórtmúyeshlikler sızıń. Olardıń maydanın esaplań. Tárepleri qanday bolǵanda maydanı eń úlken boladı? Qanday kórinis bolǵanda maydanı eń úlken boladı?

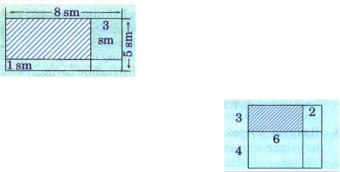
Súwrettegi kórinistiń maydanı 680 sm2 bolsa, berilgen

ólshemlerden paydalanıp, x tı tabıń.

Tuwrı tórtmúyeshliktiń tárepleri uzınlıqları:

a) kvadrattıń tárepiniń uzınlıǵı: 4 sm; 5 sm; 10 sm; 15 cm; 2 dm;

25sm bolsa, onıń maydanın esaplań;

b)ólsheń hám shtrixlanǵan bólektiń maydanın esaplań.

285

a)kvadrattıń tárepiniń uzınlıǵı 4 sm. Onıń tárepleri 1 santimetrge qısqartıldı. Payda bolǵan kvadrattıń perimetrin hám maydanın esaplań;

b)kvadrattıń tárepiniń uzınlıǵı 3 sm. Onıń tárepleri 1 santimetrge uzaytırıldı. Payda bolǵan kvadrattıń perimetri hám maydanın esaplań.

a)kvadrattıń tárepiniń uzınlıǵı 4 sm. Onıń tárepleri 1 santimetrge qısqartırıldı. Payda bolǵan kvadrattıń perimetrin hám maydanın esaplań;

b)kvadrattıń tárepiniń uzınlıǵı 3 sm. Onıń tárepleri 1 santimetrge uzaytırıldı. Payda bolǵan kvadrattıń perimetrin hám maydanın esaplań.

a)tuwrı tórtmúyeshlik ultanınıń uzınlıǵı 8 sm, biyikligi 5 sm. Onıń ultanı uzınlıǵı 3 sm hám biyikligi 1 sm qısqartırılsa, maydanı qansha kemeyedi?

b) tuwrı tórtmúyeshliktiń ultanı uzınlıǵı 6 sm, biyikligi 3 sm. Onıń ultanı 2 sm hám biyikligi 4 sm uzaytırılsa, maydanı qansha artadı?

a)kvadrattıń tárepiniń uzınlıǵı 4 sm. Onıń tárepleri 1 santimetrge qısqartırıldı. Payda bolǵan kvadrattıń perimetrin hám maydanın esaplań;

b)kvadrattıń tárepiniń uzınlıǵı 3 sm. Onıń tárepleri 1 santimetrge uzayttırıladı. Payda bolǵan kvadrattıń perimetri hám maydanın esaplań.

286

Bólek betke tárepiniń uzınlıǵı 4 sm bolǵan kvadrat sızıń. Onıń qarama-qarsı ushların birlestiriń.

a)kvadrat neshe úshmúyeshlikke ajıratıladı? Olardı kesip alıń. Ústpe-úst qoyıp, teńligine isenim payda etiń.

b)bul úshmúyeshliklerden 2 kvadrat, tuwrı tórtmúyeshlik jasań. Payda bolǵan kórinislerdi dápterge sızıń. Hár bir kórinistiń maydanın bólek-bólek tawıp, jazıp qoyıń.

Súwrette sızılǵan kórinistiń beti 240 sm2 bolsa, berilgen ólshemlerden paydalanıp, x tı tabıń.

Kvadrattıń tárepiniń uzınlıǵı 4 sm. Onıń tárepleri 4 márte qısqartıldı. Payda bolǵan kvadrattıń maydanın tabıń.

Tuwrı tórtmúyeshliktiń maydanı 36 sm2. Onıń bir tárepiniń uzınlıǵı 4sm. Ekinshi tárepiniń uzınlıǵın tabıń.

Sheshiw. S=a∙b formulaǵa qarap 36 sm2 =4∙x, bunnan x=36:4=9 (sm).

Juwap: x=9 sm.

Úshmúyeshliktiń tárepleriniń uzınlıqları 10 sm, 7 sm hám x sm. Perimetri bolsa 30 sm. Belgisiz tárep uzınlıǵın tabıń.

Úshmúyeshliktiń eki tárepiniń uzınlıǵı 1 dm 8 sm. Onıń perimetri 3 dm 2 sm bolsa, úshinshi tárepin tabıń.

Úshmúyeshliktiń bir tárepiniń uzınlıǵı ekinshisinen 3 sm uzın, úshinshisinen 5 sm qısqa. Eger onıń perimetri 38 sm bolsa, hár bir tárepiniń uzınlıǵın tabıń. Máseleni hár túrli usılda sheshiń.

Úshmúyeshliktiń tárepleriniń uzınlıqları x sm, x sm hám 12 sm. Onıń perimetri 48 sm bolsa, tárepleriniń uzınlıǵın tabıń.

287

Úshmúyeshliktiń úsh tárepiniń uzınlıqları ózara teń. Perimetri bolsa 51 sm. Sol úshmúyeshliktiń tárepiniń uzınlıǵın tabıń.

a)kvadrattıń 4 múyeshi kesip taslandı. Qanday figuralar payda bolıwı múmkin? Sáykes figuralar jasań;

b)kvadrattıń úsh múyeshi kesip taslandı. Qanday figuralar payda bolıwı múmkin? Sáykes figuralar jasań.

a) barlıq eki xanalı sanlar sanı barlıq tórt xanalı sanlar sanınan neshe márte kem?

b)barlıq úsh xanalı sanlar sanı barlıq bir xanalı sanlar sanınan neshe márte kóp?

Kesteni toltırıń, bul jerde P-tuwrı tórtmúyeshliktiń perimetri, a- ultanı, b-biyikligi, P=2(a+b)

Kvadratlar hám úshmúyeshlikler ishine qanday sanlar qoyılsa, teńlik tuwrı boladı?

Kórinistegi hár bir tuwrı tórtmúyeshliktiń maydanın esaplań. ABCD nıń maydanı qaysı tuwrı tórtmúyeshlikler maydanları qosındısına teń?

Tuwrı tórtmúyeshlik qońsı tárepleriniń uzınlıqlarınıń qosındısı a+b=8 dm bolsa, kesteni toltırıń:

288

a) tárepleriniń uzınlıǵı haqqında ne dey alasız? b) maydanı hám perimetri haqqında she? d) maydanı qay waqtta eń úlken bolar eken?

Perimetri 36 sm bolǵan tuwrı tórtmúyeshlik tárepleriniń uzınlıǵın kestege jazıp shıǵıń hám maydanın esaplań. Tuwrı tórtmúyeshliktiń maydanı qay waqıtta eń úlken boladı?

Maydanı 72 sm2 bolǵan tuwrı tórtmúyeshliklerdiń bir tárepiniń uzınlıǵına qarap basqa tárepiniń uzınlıǵın hám perimetrin tabıń:

Nızamlardı uǵıp aldıńız ba? Juwmaq shıǵarıń.

13-§. ÚLES HÁM BÓLShEK TÚSINIGI MENEN

TANÍSTÍRÍW METODIKASÍ

1. Bólshekler menen tanıstırıwdıń mazmun

Oqıwshılardı bólshekler menen tanıstırıw dástúr boyınsha 3- klastan baslanadı. Bólsheklerdiń payda bolıwı, olardı salıstırıw, sannıń úlesin tabıw hám berilgen úleske qarap sannıń ózin tabıw menen tanısadı. 4-klasta 1 diń úlesi hám bir neshe úlesti hám onıń jazba kórinisi pikirine iye boladı. Bólshek túsinigi geometriyada kesindi úlesi, shamalardıń úlesi hám basqa geometriyalıq kórinislerdiń úlesleri menen tuwrıdan-tuwrı baylanısqan.

289

Bólshek túsinigin payda etiw hár túrli nárselerdi teń bóleklerge bóliw, kesiw, sındırıw, maydalawdan kelip shıǵadı delinedi. Baslawısh klastan aldın, yaǵnıy mektepke shekemgi jasında-aq bólshek túsiniginiń dáslepki túsinikleri berilgen. Mısalı, alma, ǵarbız, qıyar, nan hám basqalardı bir neshe bóleklerge bólip kórgen hám dáslepki túsinigin alǵan. Sol maqsette balalardı úlesler menen, olardıń jazılıwı menen tanıstırıw, salıstırıwdı úyretiw, sannıń úlesleri hám úlesi boyınsha sandı tabıwǵa baylanıslı máselelerdi sheshiw názerde tutıladı. Aytıp ótilgen barlıq máseleler kórgizbeli etip ashıp beriledi.

2. Shamalardıń úlesleri menen tanıstırıwdıń metodikası

Joqarıda kórgenimizdey, 3-klasta birdiń úlesleri, yaǵnıy 1/2, 1/3, 1/4 hám basqa da úleslerge baylanıslı pikirlerdi payda etiwden ibarat. Bólsheklerdi úyretiw derlik kórgizbe tiykarında túsindiriledi. Bul kórgizbelerge miywe, qawın, ǵarbız, geometriyalıq kórinis, shóp, qaǵaz hám basqa átiraptaǵı nárselerdi alıw múmkin.

Kórgizbeli túsindiriwde, mısalı, almanı teń ekige bóliw, járdeminde bólshek payda etiledi. Soǵan sáykes almanı teń bolmaǵan 2 bólekke bólip, ol yarım alma emesligin, demek, bólshekti payda etpeytuǵının túsindiriw kerek. Tek ǵana teń bólekke bólgende bólshek san yamasa pútinniń úlesi payda bolıwın bekkemlep sińdiriw kerek.

Hár túrli geometriyalıq kórinisler menen islep atırǵanda bul kórinis járdeminde úleslerdi payda etedi, hám de onıń ayırım qásiyetlerin keltirip shıǵaradı. Mısalı, kvadrattı teń 4 bólekke bóliwde, onı eki jol menen bólip, múyeshlerdiń ózara teńligine, hám de tárepleriniń de ózara teńligine tiykarlanıp, sonday-aq kvadrat simmetriyası haqqında túsinikke iye boladı.

290

Sonday-aq, basqa oqıwshılarǵa dóńgelekti, ayırımlarına tórtmúyeshliklerdi 4 bólekke bóliw tapsırıladı. Bunnan keyingi jumıs teń bóleklerge bólingen úleslerden birewin, ekewin, úshewin alıp olardı qanday sanlar menen jazıw kerekligi úyretiledi. Bólsheklerdi

arasındaǵı baylanıslardı payda etiw kerek. Sol tiykarda alım hám bólim hám de bólshek sıyaqlı jańa terminler kirgizbesten oqıladı. Biraq sızıq sızıw, sızıqtıń tómeninde pútindi neshege bólgen san, joqarısına neshe úlesti alǵan san jazılıwı túsindiriledi.

«Úlesler» temasında figuralardı teń bóleklerge bóliw tiykarında úleslerdi salıstırıw da túsindiriledi. Mısalı, oqıtıwshı 5 birdey tuwrı tórtmúyeshli qaǵazdan jolaqsha etip qırqıwdı usınıs etedi.

Bul jolaqshanıń birinshisin teń ekige, ekinshisin teń tórtke bólip, olardı ústpe-úst qoyıw tiykarında hár bir teń bóleklerdi salıstıradı. Onda 1/2>1/4, 1/4>1/8, 1/3>1/6 sıyaqlı ekenligine isenim payda etedi. 3-klasta sannıń úlesin tabıwdı ámeliy máselelerden baslaw kerek. Mısalı, uzınlıǵı 12 sm bolǵan qaǵaz jolaqshanı alıp onı ekige búklew tapsırıldı. Jolaqshanıń yarımı neshe sm? 12/2=6 sm. Endi jolaqshanı jáne eki búklep tórt bólimge bóledi. Jolaqshanıń qanday bólimi payda boldı hám onıń uzınlıǵı qansha? Juwap: 12:4=3 sm. 1/4 , bólim. Bul jumıs sızǵısh járdeminde de ólshep kóriledi.

Másele. Kitap 80 bet, oqıwshı onıń 1/4 bólegin oqıdı. Neshe bet kitap oqıǵan. 80 bettiń 1/4 bólegi qansha?

80:4=20 bet.

1.Basqa máselelerdi sheship atırǵanda sızılmadan paydalanıw jetkilikli: san kesindi arqalı súwretlengen, ol berilgen sandaǵı teń bóleklerge bólinedi, úlesi belgilenedi, soń sheshiw awızeki yamasa jazba orınlanadı. Mısalı, 1/2 m de, 1/4 m de, 1/5 m de neshe sm bar? 1/2 saatta, 1/5 saatta 1/6 saatta neshe minut bar?

Waqıt ólshemlerin úyrenip atırǵanda ne ushın «bir yarım», «sherek kem 10» dep aytılıwın túsindiriwi kerek. Kerisinshe, sannıń úlesine qarap sannıń ózin tabıwǵa da úlken itibar beriledi. Mısalı, «TU-104» samalyot 1/3 minutta 5 km ushadı. 1 minutta neshe km ushadı? 1/3 bólegi 5 km bolǵan san neshe?

5∙3=15 km

291

2.Keyingi waqıtları, sandı onıń úlesi boyınsha tabıwǵa baylanıslı máseleler menen sannıń úlesin tabıwǵa baylanıslı máseleler aralastırılıp kiritiledi. 3-klasta úlesti hám úleske qarap sandı tabıwǵa baylanıslı tek ápiwayı máseleler, 4-klasta bolsa quramalı máseleler sheshtiriledi.

3. Bólsheklerdi úyreniw metodikası

«Úlesler» temasına tiykarlanıp bólsheklerdiń payda bolıwı menen 4-klasta tanıstırıladı. Bul jerde de kórgizbe qural bilim beriwdiń bas qaǵıydası boladı. Zatlardı, kórinislerdi hám basqa átiraptaǵılardı teń bóleklerge bóliw hám sol bóleklerden birewin, ekewin, úshewin,… alıw máselesi, onı ańlatıw, hám jazıw tiykarǵı wazıypa boladı. Bunda bólshek, bólshektiń alımı, bólimi sıyaqlı terminler menen tanıstırıladı.

Bólsheklerdi jazıwdı orınlawda tómendegi qaǵıydaǵa ámel etiw esletiledi. Sızıq astına jazılǵan san bólshektiń bólimi dep, pútin nárse neshege teń bóliniwin ańlatadı. Bólshektiń ústine jazılǵan san bólshektiń alımı dep, teń bóleklerden qanshası alınǵanın kórsetedi. Baslawısh klasta bólimi 10 nan úlken bolmaǵan bólshekler qaraladı.

Bunnan keyin bólsheklerdi maydaraq úleslerge maydalaw hám kerisinshe máseleler qaraladı. Mısalı, 3/4=6/8 yamasa 2/8=1/4 lerdi túsindiriw ushın birdey jolaqsha alamız hám 1-sin 4 teń bólekke, 2- sin 8 teń bólekke bólip, 1-sinen 3 úlesti, 2-sinen 6 úlesti alamız. Bul eki jolaqshadaǵı maydanlar teńligi kórinip turadı. Sonday-aq 2/8=1/4 ańlatpa túsindiriledi.

Sannıń bólshegin tabıwǵa baylanıslı máselelerdi sheshiwde 3- klasta úyrenilgen sannıń úlesin tabıw máselesi tiykar bolıp xızmet etedi.

Másele. Uzınlıǵı 10 sm bolǵan kesindi sızılǵan, 3/5 bólegi neshe sm ge teń. Uzınlıǵı 10 sm bolǵan kesindini sızadı hám onıń 1/5 úlesi neshe sm ekenligin 3-klastan biledi. 10:5=2 sm. Soń kesindiniń 3/5

292

bólegin tabıwda 2∙3=6 sm jumıstı orınladı, yamasa birden 10:5∙3=6 sm dep orınlaw da múmkin.

Másele. Dápter 24 betlik, oqıwshı dápterdiń 5/8 bólegin toltıradı. Neshe bet jazılmay qaldı? Másele shártiniń qısqasha jazılıwı tómendegishe:

Bar edi-24 bet. Jazıldı-5/8 bólegi.

Qaldı-?

Sheshiw. Máseleni sheshiwde kesindi sızılmasınan paydalanamız. Kesindini 24 bet dep alıp, onı 8 teń bólekke bólemiz hám onıń 5 bólimin ajıratamız.

1)24:8= bet

2)3∙5=15 bet

3)24-15=9 bet jazılmadı.

Ulıwma ańlatpa kórinisinde 24-24:8∙5=9 bet.

4-klass sabaqlıǵında berilgen sannıń bólegin tabıwǵa baylanıslı ayırım máselelerdi sheshiwde úlken, quramalı ańlatpalar payda boladı. Bunday máselelerdiń sheshimlerin ámellerdi orınlaw járdeminde ańlatıw kerek boladı. Mısalı: oramda 240 m sım bar edi. Sol sımnıń 5/8 bólegin isletildi. Qalǵanınan neshe metr artıq sım isletilgen?

Sheshimniń ańlatpa kórinisindegi jazıwın tómendegishe orınlaymız:

1)240:8∙5=150 m.

2)240-150=90m.

3)150-90=60m.

Ulıwma ańlatpası 240:8∙5-(240-240:8∙5)

Bólsheklerdi salıstırıwda teń tuwrı tórtmúyeshliklerdiń kórinislerinen de paydalanıw qolaylı. Oqıwshılarǵa dápterlerine boyı

16 sm ge, eni bolsa 1 sm bolǵan tuwrı tórtmúyeshlik sızıw tapsırıladı. Bul bir tuwrı tórtmúyeshlikke 1 sanın jazamız. 1-tuwrı tórtmúyeshlik astında sonday tuwrı tórtmúyeshlik sızıń hám onı teń ekige bóliń. Qanday úlesler payda ettińiz? (ekiden bir, yarım úlesler).

Astına sonday tuwrı tórtmúyeshlik sızıń hám onı teń tórt bólekke bóliń. Hár bir bólek ne dep ataladı hám qanday san menen ańlatıladı? 1 pútinde neshe sherek (tórtten bir) bar? Yarımda neshe

293