Matematikani oqitiw metodikasi

Sonnan soń hár túrli figuralar sızılǵan (mısalı, 4-súwrette keltirilgenindey) qaǵazlardı tarqatıp, olardıń maydanların salıstırıwdı usınıs etedi.

Bunıń ushın usı figuradaǵı shaqmaqlar sanın sanap shıǵıw kerekligin balalardıń ózleri ańlap jetedi. Figura maydanı qansha úlken bolsa, shaqmaqlar sanı da kóp boladı. Balalarǵa 5-súwrette súwretlengen figuralar maydanların ózara salıstırıwdı usınıs etiw múmkin. Bunıń aqıbetinde jáne bir ólshem-úshmúyeshlikti de tańlaw imkaniyatı tuwıladı.

Maydanlardı salıstırıwda birdey ólshemnen paydalanıw zárúrligine balalar dıqqatın qaratıw kerek. Bunıń ushın (súwret 6) hár túrli kvadratlarǵa bólistirilgen kórsetpe figuralardan paydalanıw múmkin. Oqıtıwshı figuralar ishindegi kvadratlardı sanawdı usınıs etedi. Kvadratlar sanı birdey bolıp shıǵadı.

– Bul kvadratlardıń maydanların teńdey dew múmkin be?,-dep soraladı. Sózsiz joq, sebebi kvadratlar sanı birdey bolǵanı menen maydanları teń emes.

Balalar kesindi uzınlıǵı menen tanısıw dáwirinde orınlaǵan shınıǵıwlardan paydalanıw múmkin.

«Úsh oqıwshı bir maydan betin ólsheydi, olardan birinshisiniń juwabı-8, ekinshisi 4, úshinshisi-2 edi. Nege bunday boldı?

Balalardıń qay biri maydandı durıs ólshedi? (figura dápterge sızıladı) oqıwshılar ólshew waqtında bala óz ólsheminen paydalanǵanlıǵı sebepli úsh túrli juwap alınǵanın túsinip jetedi. Oqıtıwshı úsh

ólshemdi hár túrli reńlerge boyaydı. Bul sıyaqlı shınıǵıwlar oqıwshılardı ólshem ushın tek ǵana bir birlik-1 kv sm. (hár tárepi bir sm kv ólshem birligi)in ulıwma ólshem birligi sıpatında qabıl etiw pikirine alıp keledi. Hár bir oqıwshıdan bir kv sm. ólshem modeli bolıwı kerek. Maydan betin ólshew proсesi oqıwshılar tárepinen jaqsı ózlestiriwi ushın balalarǵa hár túrli geometriyalıq kórinisler berilip, olardı 1 kv sm. model menen ólshew usınıs etiledi. Bul tapsırma sol tárepi menen belgili, figuralar betin ólshew dawamında olar figura maydanı qansha kvadrat santimetrden ibarat ekenin biliwge háreket etedi. Oqıwshılar-1kv. sm. ólshem modeldi figura betine jaylastırıp, esaplap shıǵıw qıyın. Kvadrat tor shaqmaqlar sızılǵan juqa qaǵazdan paydalanıw bolsa bir qansha qolay ekenin túsinip jetedi. Sonıń menen balalar paletkadan paydalanıwdı

184

úyrenip, onıń járdeminde hár túrli figuralar betin tabıw boyınsha shınıǵıwlar orınlaydı.

Tuwrı múyeshli tórtmúyeshlikler maydanın anıqlawda ámeliy usıllardan kóp paydalanıw kerek. Bul usıl-tuwrı tórtmúyeshlikte neshe 1 sm kv modul ólshemi barlıǵın kórsetedi. Bunı jáne de qolaylıraq jol menen-tuwrıtórtmúyeshlik enin boyına kóbeytiw menen de tabıw múmkin.

1-tapsırma. Maydan ólshem birliklerinen - kvadrat deсimetrdi kiritiwde tómendegishe jol tutıw múmkin.

Oqıtıwshı taxtaǵa tuwrı tórtmúyeshlik sızıp balalarǵa, eki model kvadrat santimetr hám kvadrat deсimetrden paydalanıp, usı maydandı ólshewdi tapsıradı.

Bunday jaǵdayda balalar santimetr modelinen paydalanıw qolaysız ekenin sezedi. Kvadrat deсimetr modelinen paydalanıw ámelde qolaylı ekenin biledi. Hár bir balada kvadrat santimetrlerge bólinetuǵın kvadrat deсimetrler modeli bolıwı hám bul model ortasındaǵı baylanıs 1 kv dm = 100 kv sm ekenin túsinip jetedi.

Kvadrat metr modeli menen tanıstırıw proсesinde kvadrat deсimetrlerge bólingen kvadrat metr model bolıwı kerek. Hár túrli shınıǵıwlardı orınlaw dawamında maydan ólshem birlikleri ortasındaǵı baylanıs yadqa (miyge) ornalasıp qaladı.

2-tapsırma. Matematika sabaqlıǵınan maydan betiniń ólshem birliginiń ózara qatnasına baylanıslı shınıǵıwlar tabıń. Bul shınıǵıwlardı orınlaw waqtında oqıwshılardıń pikirlesiwine imkaniyat beriń.

Matematikada úyreniletuǵın tiykarǵı túsiniklerden biri shama túsinigi bolıp tabıladı. Baslawısh klaslarda uzınlıq, zattıń massası hám kólemi, waqıt, figuranıń maydanı sıyaqlı shamalar úyreniledi.

Baslawısh klaslarda bul shamalardı tiykarǵı shamalar dep ataydı. Bunnan tısqarı, baslawısh klass oqıwshıları ayırım shamalar (tegis háreket tezligi hám basqalar) menen de tanısadı. Bunday shamalardı úyreniwde olardı ólshew máselesi úyrenilmeydi.

Kesindi uzınlıǵı túsinigi - predmetlerdiń uzınlıǵı boyınsha salıstırıw tiykarında kiritiledi.

Ámeliy jumıslar sózler járdeminde ańlatılıwı menen baqlanadı. «Uzınlıqları boyınsha teń», «teń emes» sózleriniń mazmunları «birdey», «uzınıraq» sıyaqlı sózler menen ańlatıladı.

185

1)Berilgen kesindini ólshew;

2)Berilgen uzınlıqtaǵı kesindini jasaw (sızıw) máselesin sheshiw kerek.

Bul máseleni sheshiwdiń 2 túrli usılın ajıratıw múmkin. Birinshi usıl - ústine qoyıw usılı.

Bul usıldıń mánisi sonnan ibarat ólshenip atırǵan yamasa alınıp atırǵan kesindi santimetrdiń modelleri menen hám olardıń sanı sanap shıǵıladı. Bunday jumıs balalardıń hár biri sm di «bayqawında», sezilerli járdem beredi.

Ekinshi usıl - qoyıp barıw usılın izbe-iz orınlaw.

Oqıwshılar ólshewde sızǵıshtaǵı sızıqlardı emes, bálkim kesindige ólshem neshe márte jaylasıwın anıqlawdı úyrenip alǵanınan soń сifrlar menen belgileydi.

Sanaw basınan sızǵıshqa 0 сifrı menen belgileniwi haqqında gúrriń. Ayırım mámleketlerde (Chexiyada) santimetrler shkalasınıń dáslepki sızıqshasın nol menen belgilemeytuǵın arnawlı sızǵıshtan paydalanılmaydı.

Oqıwshılardı uzınlıqtıń jańa birligi deсimetr menen tanıstırıwda ekinshi onlıqtı úyreniw múnásibeti menen baslanadı. Deсimetr modeli járdeminde ólshewde ayırım shınıǵıwlardı keltiremiz.

Waqıtqa baylanıslı túsiniklerdi qáliplestiriw, waqıt ólshemlerin úyreniw hám de tiyisli uqıplılıq hám kónlikpelerdi qáliplestiriw metodikası.

2-klasta «Waqıt ólshemleri» temasın úyretiwde balalar waqıt ólshemleriniń tiykarǵı birlikleri haqqında konkret túsinikke iye bolıwı kerek. Bular jıl, hápte, sutka, saat, minut.

Oqıtıwshınıń wazıypası oqıwshılardı waqıttı anıqlawında saattan

ámelde paydalanıwǵa, sonday-aq, hádiyseniń qansha waqıt dawam etkenligin, baslanıwı hám aqırın anıqlaw menen baylanıslı bolǵan hár qıylı máselelerdi sheshiwde tabel kalendardan paydalanıwǵa úyretiwden ibarat.

186

Belgili bolǵanınday, waqıt ólshemleri, ólshemlerdiń metrlik sistemasınan parıq etip tuwrıdan-tuwrı ólshew imkaniyatın bermeydi. Bul jaǵday hár túrli kórgizbeli qollanbalardan paydalanıw kerekligin kórsetedi.

1.Tabel-kalendar. Usı jıl ushın bunday tabel-kalendardı oqıwshılardıń ózleri oqıtıwshı basshılıǵında miynet sabaqlarında tayarlaydı.

2.Saatlardıń kórsetiwshi modelleri.

3.Mektep oqıwshısınıń kúndelik rejimli kesteleri.

Birinshi sabaqta balalarda jıl, ay, hápte haqqındaǵı túsiniklerdi qáliplestiriwge baylanıslı jumıslar orınlanadı.

Jılda aylardıń keliw tártibin bekkemlew maqsetinde rim сifrları (I-IX) kiritiledi.

Sutka túsinigi sutkanıń balalarda tanıs bólekleri bolǵan erte, kúndiz, keshqurın, tún túsinikleri arqalı kiritiledi. Onnan tısqarı waqtınsha tómendegi izbe-izlikke tiykarlanadı: ótken kúni, keshe, búgin, erteń, erteńnen keyin. Oqıwshılarǵa kalendardaǵı sáneler sutkalardı ańlatıwdı, sutkalar keshqurın saat 12 de baslanıwın túsindiriw kerek.

Sonnan keyin saat hám minut qaraladı. Mámleketimiz turmısınan alınǵan mısallar, zavod hám fabrikalar 1-minutta, 1-jumıs kúninde qansha ónim islep shıǵarıwı haqqındaǵı san maǵlıwmatlar úlken áhmiyetke iye.

Saat hám minut penen tanıstırıwǵa baǵıshlanǵan birinshi sabaqta-aq waqıt ólshemleri arasındaǵı múnásibetler aytıladı: bir sutka 24 saattan, 1-saat 60 minuttan ibarat.

Sabaq úlgisi

Oqıwshılardıń kún tártibi.

1.1 sutkada neshe saat bar? Siz sutkada neshe saat uyıqlaysız? Awqatlanıwıńızǵa qansha saat waqıt ketedi? Bir sutkada qansha saat mektepte oqıwda bolasız? Qansha waqıt ashıq hawada dem alasız?

2.Ózińizdiń oqıwǵa bolǵan qızıǵıwshılıǵıńızdı qansha saatta arttırasız? Kúnine neshe saat oqıysız?

3.Siz bir kúnlik jumıs rejeńizdi dúzip aldıńız ba?

187

Kúnlik rejege ámel qılasız ba? Kúnlik rejeńizdi tártip penen jazıp shıǵıń.

4. Oqıwshılar ushın tómendegi jumıs kún tártibi belgilep berilgen, siz oǵan ámel qılıwǵa úyreniń.

Sabaq úlgisi

Awırlıq ólshemlerin tártipke keltiriw.

Awırlıq ólshem birliklerin yadqa túsiriw kerek: Olar dápter artında boladı.

1.Úlken massalardı ólshew ushın tonna (t), сentner (с) birlikleri

2. Ustaxanada bir neshe kóylek hám kóylekler qansha bolsa, sonsha kostyum tikti. Bir kóylekke 3 m, bir kostyumǵa 4 m material sarıplandı. Eger barlıq kóylekke 24 m material sarıplanǵan bolsa, sonsha kostyum ushın qansha material sarplanǵan?

Eger, tuwrı tórtmúyeshliktiń eki qońsı tárepi a sm b sm bolsa, maydanı S=aˑb boladı, perimetri bolsa P=2(a+b) formula menen esaplanadı.

Eger ayırım dene V tezlik penen t waqıtta S aralıqtı basıp ótse ol jaǵdayda formulalar orınlı.

188

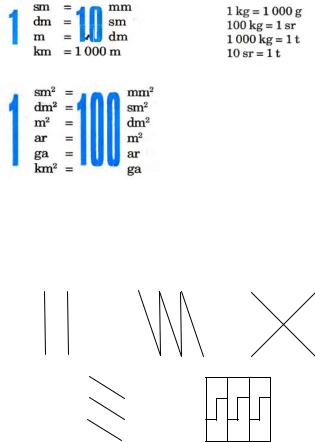
Uzınlıq ólshemleri:

Bul figuralarda ne ulıwma? 3-figura basqalarınan nesi menen parıq qıladı?

189

7-§. TERIS EMES PÚTIN SANLAR ÚSTINDE ARIFMETIKALÍQ ÁMELLERDI ÚYRETIW METODIKASÍ HÁM ESAPLAW KÓNLIKPELERIN QÁLIPLESTIRIW

Usı tema ústinde islewde oqıtıwshı aldında turǵan tiykarǵı maqsetler tómendegilerden ibarat:

1)Oqıwshılardı qosıw hám alıw, kóbeytiw hám bóliw ámelleriniń mazmunı menen tanıstırıw;

2)Esaplaw usıllarınan oqıwshılardıń ańlı paydalanıwın támiyinlew:

a) «sandı bólimleri boyınsha (birimlep yamasa gruppalap) qosıw hám alıw» usılı.

b) Qosındınıń orın almastırıw qásiyetinen paydalanıp qosıw usılı;

v) Sanlardı alıwda qosıwdıń tiyisli jaǵdayın biliwden yamasa qosındı hám qosılıwshılardan biri boyınsha ekinshi qosılıwshını tabıw uqıplılıǵınan paydalanǵan jaǵdayda qosındı menen qosılıwshılar arasındaǵı baylanıslardı biliwge tiykarlanǵan alıw usılı.

3.Qosıw hám alıw, kóbeytiw hám bóliw kónlikpe uqıplılıqların qáliplestiriw (yadlap alıwǵa jetkeriw) 10 ishinde qosıw hám alıwdı úyreniw jumısın ózara baylanısqan bir neshe basqıshqa bóliw múmkin. Oqıwshılarda awızeki hám jazba esaplaw kónlikpelerin qáliplestiriw matematika dástúriniń tiykarǵı baǵdarlarınan biri.

Arifmetikalıq ámellerdi úyreniwden aldın balalar sanasına onıń mánisi, mazmunın jetkeriw kerek. Bul wazıypa hár túrli ámeliy jumıslardı orınlaw tiykarında ótkeriledi. Mısalı, «onlıq» temasınıń qosıw hám alıw ámelleriniń mánisi 2 kóplik elementlerin birlestiriw hám kóplikten onıń bólimlerin ajıratıw sıyaqlı ámeller járdeminde

alıp barıladı. Kóbeytiwdi onıń komponentleri menen nátiyjesi ortasındaǵı baylanıslardı úyreniw bolsa bóliw ámelin úyreniw ushın tiykar bolıp xızmet etedi.

Demek, oqıtıwdıń 1-basqıshında abstrakt bolǵan nárse gezektegi basqıshta jáne de abstraktlıraq bilimlerdi qáliplestiriw ushın anıq tiykar bolıp xızmet etedi. Hár túrli esaplaw usıllarınıń ózlestiriliwi ushın dástúrde arifmetikalıq ámellerdiń ayırım kerekli qásiyetleri hám olardan kelip shıǵatuǵın nátiyjeler menen tanıstırıwdı názerde

190

tutadı. Mısalı, 1-klasta 10 ishinde qosıw hám alıwdı úyreniwde balalar qosıwdıń orın almastırıw qásiyetleri menen tanısadı. Dástúrde arifmetikalıq ámellerdiń qásiyetlerin úyreniwden tısqarı arifmetikalıq ámel aǵzaları hám nátiyjeleri arasındaǵı baylanıslardı tanıstırıwdı da názerde tutadı. Bul jumıs ámellerdi, teńlemelerdi tekseriwde kerekli áhmiyetke iye. Mısalı, 6∙4=24 bolsa, onı bóliwge baylanıstırıp 24:6=4, 24:4=6 sıyaqlı jaǵdaylar payda etiledi.

Kerekli wazıypalardan biri esaplaw kónlikpelerin qáliplestiriw bolıp tabıladı. Awızeki hám jazba usılda esaplawlar 1-4-klastıń hár bir temasında óz sáwleleniwin tapqan.

Mısalı, awızeki

276+432=(200+400)+(70+30)+(6+2)=600+100+8=708 Jazba, 276

+ 432

Sonday jaǵdayǵa jetkeriw kerek, arifmetikalıq ámellerdi orınlaw avtomatizmge aylansın.

Arifmetikalıq ámellerdi úyreniwde aldın oqıwshılar ańına onıń mánisin, mazmunın jetkeriw kerek. Bul jumıs predmetlerdiń hár qıylı kóplikleri menen ámeliy jumıslar orınlaw ótkeriledi.

Oqıwshılardı qosıw hám alıw ámelleriniń mánisi menen tanıstırıw eki kóplik elementlerin birlestiriwge baylanıslı hám berilgen kóplikten onıń bólimlerin ajıratıw sıyaqlı ámeliy qatnaslar arqalı ámelge asırıladı. Qosıw ámeli sanlardı kóbeytiw ámelleri tiykar bolıp xızmet qıladı. Kóbeytiw onıń komponentleri menen nátiyjeleri arasındaǵı baylanıslardı úyreniw óz náwbetinde bóliw ámelin úyreniw ushın tiykar bolıp xızmet qıladı. Arifmetikalıq ámellerdi

úyreniwdegi máselelerden biri awızeki hám jazba esaplaw usılların ańlı ózlestiriw, esaplaw uqıplılıq hám kónlikpelerin qáliplestiriw menen baylanıslı bolıp esaplanadı. Awızeki esaplawlardıń tiykarǵı kónlikpeleri I hám II klaslarda qáliplesedi. Awızeki esaplaw usıllarıda, jazba esaplaw usıllarıda ámeller qásiyetleri hám olardan kelip shıǵatuǵın nátiyjelerdi ámeller menen nátiyjeleri arasındaǵı baylanıslardı biliwine tiykarlanadı. Biraq, awızeki hám jazba esaplaw usıllarınıń parıq qılıwshı qásiyetleride bar.

Awızeki esaplawlar:

1. Esaplawlar jazıwlarsız (yaǵnıy yadta orınlanadı) yamasa jazıwlar menen túsindirip beriliwi múmkin.

191

Bunda sheshimlerdi:

a) túsindiriwlerdi tolıq jazıw menen (yaǵnıy esaplaw usılın dáslepki bekkemlew basqıshında) beriw múmkin. Máselen:

34 + 3 = (30 + 4 ) + 3 = 30 + ( 4 + 3) = 37,

9 + 3 = 9 + ( 1 + 2 ) = ( 9 + 1) + 2 = 12 hám t.b.

b) berilgenlerdi hám nátiyjelerdi jazıw múmkin. Máselen, 34 + 4 = 37, 9 + 3 = 12.

v)esaplaw nátiyjelerin nomerlep jazıw múmkin. Máselen, 1) 37,

2)12…

2.Esaplawlar joqarı xana birliklerinen baslap orınlanadı. Máselen,

430- 210 = ( 400 + 30 ) - ( 200 + 10 ) = ( 400 - 200 ) + ( 30 - 10 ) = 200 + 20 = 220

3.Aralıq nátiyjeler yadta saqlanadı.

4.Esaplawlar hár qıylı usıllar menen orınlanıwı múmkin. Máselen,

26∙ 12 = 26 ∙ ( 10 + 2 ) = 26 ∙ 10 + 26 ∙ 2 = 260 + 52 = 312:

26∙ 12 = ( 20 + 6 ) ∙ 12 = 20 ∙ 12 + 6 ∙ 12 = 240 + 72 = 312;

26∙ 12 = 26 ∙ ( 3 ∙ 4 ) = ( 26 ∙ 3 ) ∙ 4 = 78 ∙ 4 = 312

5.Ámeller 10 hám 100, jeńilirek jaǵdaylarda 1000 ishinde hám kóp xanalı sanlar ústinde esaplawlardıń awızeki usıllarınan paydalanıp orınlanadı. Máselen: 54024:6=9004

Jazba esaplawlar:

1.Esaplawlar jazba orınlanadı. Jazba esaplawlarda sheshimin jazıw baǵana túrinde orınlanadı.

2. Esaplawlar tómengi xana birliklerinen baslanadı.

192

3.Aralıq nátiyjeler dárhal jazıladı.

4.Esaplawlar ornatılǵan qaǵıydalar boyınsha, sonıń menen birge, bir jalǵız usıl menen orınlanadı. Máselen:

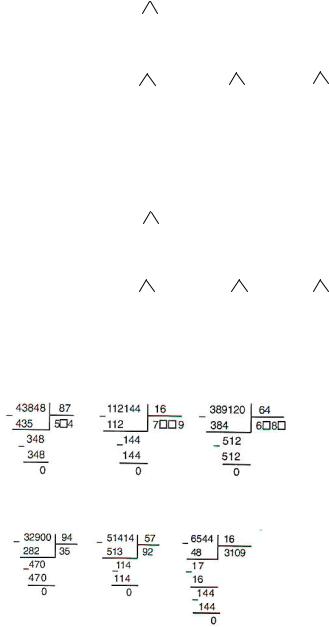
1000 ishinde hám kóp xanalı sanlar ústinde ámeller esaplawlardıń jazba usıllarınan paydalanıp orınlanadı.

Máselen:

Esaplawlardaǵı qateliklerdi tabıń hám olardı dúzetiń:

193