
Fizika pani boyinsha lekciyalar
.pdf
Gaz |
Sv, |
|
Ж |
|
Cr, |
|
Ж |
|
|
|
|
|
|
|
|
||
|
|
м о ль к |
|
м о ль к |
|
|||
|
|
|
|
|
|
|
||
Geliy (ne) |
|
12,ńh |
|
|
ǵ0,9ń |
|
||
|
|
|
|
|
|
|
||
Argon (Ar) |
|
12,ńh |
|
|
ǵá,ǵq |
|
||
|
|
|
|
|
|
|
||
Vodorod (Nǵ) |
|
ǵ0,q9 |
|
|
ǵh,wú |
|
||
|
|
|
|
|
|
|||
Azot (Nǵ) |
ǵ0,ww |
|
|
ǵh,úń |
|
|||
|
|
|
|
|
|
|
||
Kislorod (Oǵ) |
|
ǵ0,h9 |
|
|
ǵh,h9 |
|
||
|
|
|
|
|
|
|
||
Suw puwları (NǵO) |
|
ǵw,hń |
|
|
qú,ǵǵ |
|
||
|
|
|
|
|
|
|
|
|
Tájiriybede |
bolsa onıń temperaturaǵa baylanıslılıǵı anıqlanadi. |
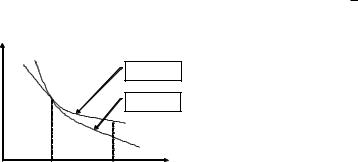
5-súwrette eki atomlı |
||
|
|
molekulalardan ibarat gazlar ushın Sv nıń temperaturaǵa |
||
|
|
baylanıslı grafigi |
berilgen. Kórinip |
turıptı, Sv tek ayrim |
(7/2)R |
|
temperatura aralíqlarında ǵana ózgermeydi hám olar |
||
|
|
|||
(5/2)R |
|
molekula erkinlik dárejesiniń turli mánisleringe sáykes |
||
|
|
keledi. Máselen, TáTǵ temperatura aralíqta i=q ge, Tq |
||
(3/2)R |
|
|
|
|
|
|
Tń temperatura |
aralíqta i=ó ge |
hám Tó dan joqarı |
T1 T2 T3 |
T4 T5 |
T, K temperaturalarda i= w ge sáykes kelgen SV nıń mánisleri |
||
5-суурет |
tájiriybeden tabıldı. Kórinip turıptı, SV nıń teoriyalíq hám |
|||
|
|
|||
tájiriybeda tabılǵan mánislari Tq Tń temperatura aralíqta sáykes keledi. Temperatura xana temperaturasınan júdá tómen bolsa yaki xana temperaturasınan júdá joqarı bolsa hám, SV nıń tájiriybeda tabılǵan mánisi teoriyalíq mánisge sáykes kelmeydi. Tómen temperaturalarda eki atomlı molekuladan ibarat gazlardıń salıstırma jıllılíq sıyımlılıǵı Sv bir atomlı molekulalardan quralǵan gazdıkine jaqın boladı. Bunıń sebebin klassik teoriya túsindire almaydı. Joqarı temperaturada jıllılíq sıyımlılıǵı keskin artıp ketiwin túsindiriw ushın klassik teoriya eki atomlı gaz molekulalarınıń joqarı temperaturada bir-birine salıstırǵanda terbelmeli háreket etedi dep qaraydı. Nátiyjede molekulalardıń erkinlik dárejesine terbelmeli háreketge baylanıslı bolǵan erkinlik dáreje sanı hám qosılıp, eki atomlı gaz molekularınıń erkinlik dárejesi ulıwma jaǵdayda
i = iil + iayl +ǵ iteb = q + ǵ + ǵ á = w
kórinisinde anıqlanadi. Terbelmeli hárekette energiya potentsial hám kinetik energiyalar ortasında teń bólistirilgeni ushın terbelmeli háreketdegi erkinlik dáreje sanı hám ǵ ge teń boladı. Demek, joqarı temperaturada SV = wR/ǵ formula orınlı boladı.
4. ADIABATIK PROTSESS. ADIABATA TEŃLEMESI
Sırtqı ortalíq menen jıllılíq almaspastan bolıp ótiwshi protsess adiabatik protsess dep ataladı. Adiabatik protsesste sistema tısqarıdan hesh qanday jıllılíq muǵdarın almaydı hám tısqarıǵa hám hesh qanday jıllılíq muǵdarın bermeydi. Sonıń ushına diabatik protsess ushın
termodinamikanıń á-nızamı tómendegi kórinisinte boladı: |
|
dU + dA = 0 |
(24) |
Adiabatik protsessti ámelge asırıw ushın gaz qamalǵan ıdıstı sırtqı ortalíqtan izolyatsiyalaw kerek. Bunıń ushın ıdıs jıllılíq hám jaqtılíq ótkermeytuǵın material menen oraladı. Bunday ıdıstaǵı gaz ústinde jumıs orınlansa, bul jumıs tolıǵınsha gazdıń ishki energiyasına aylanadi. Biraq gazdıń kólemin keskin ózgertsek, gaz qamalǵan ápiwayı ıdısta hám adiabatik
82

protsessti ámelge asırıw mumkin. Máselen, porshen menen gazdı keskin qıssaq, sırtqı kúsh orınlaǵan jumıs tolıǵı menen gaz ishki energiyasın asırıwǵa sarıplanadı. Bunda jıllılíq sırtqı ortalíqqa shıǵıp úlgermeydi. Gaz kólemin keskin úlkeytsek hám adiabatik protsess júz beredi. Nátiyjede gazdıń ishki energiyası kemeyip, gaz suwıydı
Bunday jaǵdayda orınlanǵan jumıs gazdıń ishki energiyasınınıń kemeyiwine teń boladı:
|
dA = dU |
(25) |
||
Formuladaǵı minus belgi gazdıń ishki energiyasınınıń kemeyip atırǵanlıǵın bildiredi. |
||||
Jumıs hám ishki energiya ańlatpaların |
|
esapqa alıp, |
(25) formuladan temperaturanıń |
|
ózgerisin tabamız: |
|
|
|
|
pdV = CvdT |
|
|||
Bunnan |
|
|
|
|
dT = |
|
1 |
r dV |
(26) |
|
|
|||
|
Cv |
|
||
qatnası payda boladı.
Adiabatik protsess formulasın keltirip shıǵarıw ushın gaz halatı teńlemesin r, V, T
ózgeriwshiler boyínsha differentsiyalaymiz.
rdV + Vdr = RdT dT nıń ornına onıń joqarıdaǵı (ǵú) ańlatpasın qoyamız:
rdV + Vdr = CvR rdV
yaki
|
|
R |
|
|
1 |
|
rdV + Vdr = 0 |
(27) |
|
|
||||
|
|
CV |
|
|
ańlatpanı payda etemiz.
Bundaǵı
|
|
|
|
|
|
|
|
i |
R R |
|
|
|
|||
|
|
R |
|
С v R |
|
2 |
|
i 2 |
|
||||||
|
|
|
|||||||||||||
1 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|||||||||
|
|
CV |
|
Cv |
|
|
|
|
i |
|
i |
|
|||
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||
ekenligin itibarga alsaq, (ǵw) qatnasın
rdV + Vdr = 0 kórinisinde jazıw mumkin. Bul ańlatpanı rV ge bólemiz
dV dр
V V
0
Joqarıdaǵı teńleme lnr.V funktsiyanıń differentsialı bolıp tabıladı. Sonıń ushın onı d ln(r.V )=0
kórinisinde jazıw mumkin. Bul qatnastan adiabatik protsesste basım menen kólem arasındaǵ ıbaylanıstı tabamız.
rV = const |
(28) |
Bul teńlik Puassan teńlemesi yaki adiabata teńlemesi dep ataladı.
83
6-súwrette adiabata hám izoterma sızıqlari ózara salıstırılǵan. Kórinip turıptı, adiabata sızıǵı izotermaǵa qaraǵanda tik, sebebi adiabata kórsetkishi >1. Adiabatik protsesste jumıs sistemanıń baslanǵısh hám aqırǵı ishki energiyalarınıń ayirmasına teń boladı.
|
|
|
U |
|
|
|
|
|
A = - 2 dU U1 U2 i R(T1 T2 ) |
|
|
|
|
|
U1 |
2 |
|
|
|
|
|
|
|
Р |
|
|
Adiabatik |
protsesste orınlanǵan |
jumıs sistemanıń |
|
|
Izoterma |
baslanǵısh hám aqırǵı halatları arqalı tabıladı hám protsesstiń ótiw |
||
|
|
|
|
|
|
|
|
|
jolına baylanıslı |
emes. Adiabatik protsesste |
orınlanǵan jumıs |
|
|
Аdiabata |
adiabata sızıǵı menen shegaralanǵan maydanǵa te4. Adiabatik |
||
|
|
|
|||
|
|
|
protsesste orınlanǵan jumıs izotermik protsesste orınlanǵan |
||
|
|
|
jumıstan hámiyshe kishi. Sebebi adiabatik |
keńeyiw waqıtida |
|
V1 |
V2 |
V |
sistema sırtqı ortalíqtan jıllılíq almay keńeyedi. İzotermik keńeyiw |
||
|
6-suwret |
|
waqıtında sistema temperaturasın barlíq waqıt turaqlı saqlaw ushın |
||
|
|
|
|||
sırtqı denelarden jıllılíq muǵdarın alıp turadı. Gaz izotermik suwıp atırǵanda mexanik jumıstan payda bolǵan energiyanı sırtqı ortalíqqa beredi. Sonıń ushın izotermik sistema menen sırtqı ortalíq arasında jaqsı jıllılíq ótkiziwsheńlik sharayatı bolıwı kerek. Adiabatik protsesste bolsa kerisinche, sistema ortalíq penen pútinley jıllılíq almaspawı kerek.
Bekkemlew ushın sorawlar:
1. Termodinamikanıń birinshi nızamı izoprotsesslarde qanday orınlanadı?
2. Adiabatik protsess qanday protsess hám onıń tenlemesi qanday keltirilip shıǵarıladı? 3. Ne sebepten gazlardıń turaqlı basımdaǵı jıllılíq sıyımlılıǵı turaqlı kólemdegiden úlken? 4. Gazdıń keńeygende orınlaǵan jumısı qanday esaplanadı.
5. Adiabatik protsesste orınlanǵan jumıs úlkenbe yaki izotermik protsesstegi me? 6. Molekulalardıń erkinlik dáreje sanı ne?
7. Gazdıń turaqlı kólem sharayatındaǵı salıstırma jıllılíq sıyımlılıǵı temperaturaǵa qanday baylanısqan?
12-tema. Termodinamikanıń II - nızamı
Jobası:
1. Qaytımlı, qaytımsız hám aylanba protsessler.
2. Jıllılíq dvigatelleri hám suwıtqısh mashinalar.
3. Termodinamikanıń II-nızamı.
4. İdeal gaz ushın Karno tsikli hám onıń p.j.k. 5. Entropiya. İdeal gaz entropiyasi.
Tayanısh sózler hám túsinikler :qaytımlı, qaytımsız hám aylanba protsessler, sistemanıń halatı hám fazası, jıllılíq hám suwıtqısh mashinaları, jıllılíq mashinasınıń paydalı jumıs koeffitsienti (PJK), termodinamikanıń ekinshi nızamı, Karno tsikli, Karno tsiklinıń PJKsı, ideal jıllılíq mashinasınıń PJKsı, temperaturanıń termodinamik shkalasi, keltirilgen jıllılíq muǵdarı,
84
sistema entropiyasi, Klazius teńsizligi, entropiyanı esaplaw, entropiya hám termodinamik itimallı3.
QAYTIMLI, QAYTIMSIZ HÁM AYLANBA PROTSESSLER
Eger bazı bir protsesske termodinamik názerden qarasaq, onıń qanday zatdan quralǵanlıǵı bizdi qızıqtırmaydı, balki onıń halatın xarakterlewchi parametrlarin biliw áhmiyetli bolıp tabıladı.
Sistema halatın anıqlaytuǵın hám sırtqı sebepler tásirinde ózgerisi mumkin bolǵan shamalar parametrler dep ataladı.
Sistemanıń parametrleri sistemanıń faza sanına baylanıslı. Faza dep, ximiyalíq quramı, dúzilisi hám halatı birdey bolǵan hám málim bet penen shegaralanǵan denege (sistemaǵa) aytıladı. Máselen, suw málim bir temperaturada úsh fazada bolıwı mumkin: suyıq, suwdıń ishindegi muz bólekleri hám onıń ústindegi suw puwı.
Eger muz hám, suw puwı hám bolmasa, yaǵnıy sistema tek suwdan ibarat bolsa, sistema bir fazali boladı. Málim bir ideal gaz hám bir fazali sistema bolıp tabıladı.Onıń halatı úsh parametr: kólem V, basım R hám temperatura T arqalı tolíq bir mánisli túrde anıqlanadi.
Eger sistema bir neshe halatlarda bolıp, jáne baslanǵısh halatına qaytıp kelse, bunday protsess aylanba protsess yaki tsikl dep ataladı.
|
|
|
|
|
Diagrammada |
bunday |
protsess |
tuyıq |
||||
Р |
а). |
Р |
|
b). |
iymek sızıq menen sıpatlanadı. Máselen, gaz |
|||||||
|
|
|
|
|
||||||||
1 |
|
|
1 |
|
keńeyip |
1-halatdan |
2 –halatǵa ótiwi |
hám |
||||
|
|
|
|
|
||||||||
|
А |
|
|
-А |
sońınan qısıw nátiyjesinde ol jáne 1-halatǵa |
|||||||
|
2 |
|
|
2 |
||||||||
|
|
|
|
|
qaytıp |
keliwi |
mumkin. |
Gazdıń |
keńeyiw |
|||
V1 |
V2 |
|
V1 |
V2 |
waqıtida |
orınlaǵan |
jumısı |
oń, |
qısılıwda |
|||
|
|
|
|
|
|
|
|
|
||||
|
|
1-suwret |
|
|
orınlaǵan jumısı bolsa teris esaplalandı (sebebi |
|||||||
|
|
|
|
|
dV<0). Aylanba |
protsesste |
orınlanǵan |
jumıs |
||||
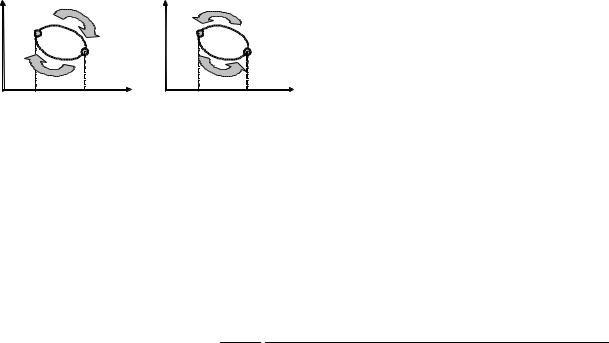
iymek sızıq penen shegaralanǵan maydan menen anıqlanadi (1-súwret). Eger tsikl saat strelkası baǵıtnida júz berse, tuwrı tsikl (1(a)-súwret). oǵan keri baǵıtta júz berse, keritsikl (1(b)-súwret) dep ataladı.
JILLILÍQ DVIGATELLERI HÁM SUWITQISH MASHINALAR
Tuwrıtsikl tısqarıdan periodlı túrde jıllılíq alıp isletuǵın jıllılíq mashinalarında (1(a)- súwret), keritsikl bolsa sırtqı jumıs esabınan isletuǵın sovitgich mashinalarıda (16.ǵ(b)-súwret) bayqaladı. Isıtqıshdan alınǵan Q1 – Q2 jıllılíq esapiga tuwrıtsikl menenish orınlaydıgan
qurılmaga jıllılíq mashinasi dep ataladı. Aylanba protsesste sistema dáslepki halatına qaytıp kelgeni ushın onıń tolíq energiyasınıń ózgerisi nolge te4. Sonıń ushın termodinamika (TD)nıń I - nızamı
Q = U + A = A |
(1) |
kórinisinde jazıladı. Biraq aylanba protsesste sistema jıllılíq alıwı hám beriwi mumkin bolǵanı ushın
Q = Q1 Q2
boladı. Bul jerde:
85

Q1- sistemanıń sırttan alǵan jıllılíq muǵdarı. Q2- sistemanıń sırtǵa bergen jıllılíq muǵdarı.
Isıtqıshdan alınǵan Qá jıllılíq muǵdarınıń birqansha bólegi A jumısına aylanǵanın biliw ámeliy áhemiyetke iye. Sonıń ushın paydalı jumıs koeffitsienti (p.j.k.) túsinigi kiritiledi.
Jıllılíq mashinasınıń p.j.k.sı
|
|
|
|
|
|
|
|
|
А |
|
Q1 - Q2 |
1 |
Q2 |
|
(2) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
Q1 |
|
Q1 |
|
|
Q1 |
|
|
||
|
|
formula menen anıqlanadi. |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Eger sistema protsess dawamında dáslepki halatına qaytıp kelmese, bunday protsess |
|||||||||||||||
|
|
qaytımsız protsess dep ataladı. Eger tuwrı hám keri protsessten soń sistema dáslepki halatına |
|||||||||||||||
|
|
|
|
|
|
|
qaytıp kelse-ol, qorshaǵan |
ortalíqta |
ózgeris |
júz bersa, |
bul |
||||||
|
|
T1 |
|
|
|
T1 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
а). |
|
|
б). |
|
protsess |
qaytımsız |
protsess |
bolıp |
tabıladı. |
Tabiattaǵı |
real |
||||||
Q1 |
|
Q1 |
|||||||||||||||
|
|
|
|
|
|
|
protsessler qaytımsız |
protsessler. |
Olarǵa kóplep mısallar |
||||||||
|
|
Jilliliq mashinasi |
|
|
|
Suwitqish |
|||||||||||
|
|
|
|
|
|
mashinasi |
keltiriw |
mumkin. Máselen: |
ıssılíq ótkeziwsheńlik, nurlanıw, |
||||||||
|
|
Q2 |
|
|
|
Q2 |
súykeliw hám basqalar. |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
T2 |
|
|
|
T2 |
№aytımlı protsesste |
sistema |
dáslepki |
halatına qaytıp |
|||||||
2-suwret |
keledi, qorshaǵan ortalíqta xech qanday ózgeris júz bermeydi. |
|
Tuwrı hám keri baǵıtta bolıp ótiwshi qaytımlı protsesste sistema bir halatdan turli baǵıtta ótiwi hám usı halatga qaytıp keliwi mumkin. №aytımlı protsess dep, hár eki baǵıtta hám óte alatuǵın hám dáslepki óziniń halatına dógerektegi denelerde hech qanday ózgeris qılmastan qaytatuǵın protsesske aytıladı.
Real sharayatda qaytımlı protsessti ámelge asırıp bolmaydı. Biraq júdá ásten bolıp ótiwshi ayrim protsessler qaytımlı bolıwı mumkin. №aytımlı protsess teńsalmaqli protsess. Ol bir neshe teńsalmaqlı halatlardıń toplamınan ibarat.
3. TERMODINAMIKANIŃ 2-NIZAMI
Termodinamik protsesslerdi túsindiriw ushın termodinamikanıń á-nızamı jeterli emes. Sebebi ol protsesstiń qanday baǵıtta bolıp atırǵanlıǵın esapqa almaydı.
Termodinamikanıń II-nızamı tarixiy tárepten jıllılíq mashinalarınıń jumısın talqılaw qılıw nátiyjesinde jaratıldı. Sonıń ushın jıllılíq dvigateliniń islew protsessi menen tanısamız (2-súwret). Jıllılíq dvigatellerinde barlíq waqıt tsikl dawamında T1 temperaturali ısıtqıshdan Q1 jıllılíq muǵdarı alınadı hám T2 tómen temperaturalı suwıtqıshga Q2 jıllılíq muǵdarın berip, A = Q1 Q2 jumıs orınlanadı. Jıllılíq mashinasınıń p.j.k.sı = á bolıwı ushın Q2 = 0 bolıwı, yaǵnıy jıllılíq mashinasi tek bir jıllılíq deregi-ısıtqıshǵa iye bolıwı hám suwıtqısh bolmaslıǵı kerek. Frantsuz injeneri N.Karno (áw9ú-áhqǵ) jıllılíq mashinası islewi ushın albette eki túrli temperaturalı ısıtqısh hám suwıtqıshtıń bolıwı zarurligin kórsetti. Termodinamikanıń II-nızamı bir jıllılíq deregi esabınan, yaǵnıy denelerdiń suwıtqısh esapbınan islewshi máńgi dvigateldiń bolıwın inkar etedi. Termodinamikanıń II-nızamına Kelvin hám Planklar tómendegishe táriyp bergen:
1) Ekinshi túr máńgi dvigateldi jaratıw mumkin emes.
2) Aqırǵı nátiyjesi ısıtqıshtan alınǵan jıllılíq muǵdarınıń tolíq jumısqa aylandırıp beretuǵın protsessti ámelge asırıp bolmaydı.
86

Suwıtqısh mashinasında Q2 jıllılíq muǵdarı temperaturası T1 bolǵan denega beriledi. Bunda T2< T1. Bizge belgili, aylanba protsesste Q = A biraq Q = Q2 Q1 < 0 shartine kóre A < 0 yaǵnıy:
|
Q2 Q1 = A1 |
yaki |
Q1= Q2 + A |
boladı. Bunnan kórinip tur, temperaturası T1 bolǵan ısıtqıshǵa berilgen jıllılíq muǵdarı, temperaturası T2 bolǵan suwıtqıshdan alınǵan jıllılíq muǵdarınan orınlanǵan jumıs muǵdarı shaması úlken bolıp shıǵıp atır. Bul sonnan dalalat beredi, jumıs orınlanbastan turıp jıllılíqtı temperaturası tómen deneden temperaturası joqarı denege ótkerip bolmaydı. Termodinamikani II-nızamı ushın bunday juwmaqtı R. Klazius bergen:
Jıllılíq hech qashan óz-ózinen temperaturası tómen deneden temperaturası joqarı denege ótpeydi.
İDEAL GAZ USHIN KARNO TSIKLI HÁM ONIŃ P.J.K.SI
Karno TD nıń II-nızamına tiykarlanıp tómendegi teoremanı shıǵaradı:
Suwıtqısh hám ısıtqıshınıń temperaturası birdey bolǵan periodlı túrde isleytuǵın barlíq jıllılíq mashinalarınıń ishinde qaytımlı protsess penen islewshi mashina eń úlken p.j.k.ǵa iye bolıp, olardıń p.j.k.sı ısıtqısh hám suwıtqıshtıń temperaturalari birdey bolǵanida bir - birine teń boladı hám mashinanıń konstruktsiyası hám jumısshı zattıń tabiyatına baylanıslı bolmaydı.
Karno úyrengen tsikl eki izoterma hám eki adiabatadan ibarat. Karno tsiklıda jumısshı dene bolıp, porshen astındaǵı ıdısda jaylasqan ideal gaz xızmet qılıwi mumkin. 16.3-súwrette Karno tsikli
sxematik kórsetilgen.
Gazdıń izotermik keńeyiwi 1-2, izotermik qısılıwi q-ń iymek sızıq penen, adiabatik keńeyiw menen qısılıw sáykes jaǵdayda 2-3 hám 4-1 iymek sızıqlar menen kórsetilgen.
Joqarıda biz izotermik hám adiabatik protsesslerde orınlanǵan jumıslardı kórip ótken edik. Usı formulalardan paydalanamız.
İzotermik keńeyiw 1-2 halat hám qısılıwda (3-4 halat) orınlanǵan jumıs tómendegi formulalar menen anıqlanar edi:
А |
m |
R T |
l n |
V2 |
Q |
|||||
|
|
|||||||||
|
12 |
|
|
2 |
|
V1 |
|
|||
|
|
|
|
|
|
|
|
|||
А |
|
m |
R T |
l n |
V3 |
Q |
|
|||
|
|
|
2 |
|||||||
34 |
|
|
2 |
V4 |
|
|
||||
|
|
|
|
|
|
|||||
Adiabatik keńeyiw (ǵ-q halat) hám qısılıwda (ń-á halat) orınlanǵan jumıs.
А23 m Cv T2 T1
А23 m Cv T1 T2
Tsikl dawamında orınlanǵan jumıs.
(3)
(4)
(5)
(6)
87

A = A12 + A23+ A34 + A41 = Q1+ A23 Q2 A23 = Q1 + A23 Q2 A23 = Q1 Q2 menen anıqlanıp, muǵdar jaǵınan shtrixlanǵan maydanǵa te4. Karno tsiklinıń p.j.k.sı
А Q1 Q2
Q1 Q1
boladı.
Joqarıda adiabatik protsess ushın shıǵarılǵan formulaǵa tiykarlanıp 2 3 hám 4 1 adiabatalar ushın
T1 V2 1 = T2 V3 1 |
|
|||||
T2 V1 1 = T1V4’ 1 |
|
|||||
formulalardan |
|
|
|
|
|
|
V2 |
|
V |
3 |
|
(7) |
|
|
|
|
|
|
||
|
V1 |
V |
4 |
|
|
|
ekenligi tabamız.
Q1,Q2 ni ornına (16.q) hám (16.ń) ańlatpalardı qoyıp hám (7) dan paydalanıp, tómengini payda etemiz.
|
|
|
|
m |
|
R T l n |
V2 |
|
m |
R T |
l n |
V3 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
Q1 Q2 |
|
|
1 |
V1 |
|
|
|
2 |
|
V4 |
|
T1 T2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Q |
|
|
|
m |
R T1l n |
V |
2 |
|
|
|
|
T |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V1 |
|
|
|
|
|
|
||||||
|
|
|
Q1 |
Q2 |
|
T1 T2 |
|
|
|
|
|
(8) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
Q1 |
|
|
|
|
|
|
T1 |
|
|
|
|
|
|
|
|
|
||
(16.h) formuladan kórinip tur, |
Karno |
tsiklinıń |
p.j.k.sı |
tek |
suwıtqısh menen ısıtqıshtıń |
||||||||||||||||||||
temperaturasına baylanıslı. Onı asırıw ushın suwıtqısh menen ısıtqıshtıń temperaturalar parqın asırıw kerek. Máselen: T1 = 400K hám T2 = 300K bolǵanda = 0,25 yaki T1 = 100K, T2 = 50K bolsa: = 0,5.
Hár qanday real jıllılíq mashinasınıń p.j.k.sı súykeliw hám jıllılíqtıń joǵalıwı bolǵani
ushın Karno tsiklnıń p.j.k.sınan kishi. |
|
Karno teoreması temperaturanıń termodinamik shkalasın jaratıwǵa tiykar boldı. |
(16.h) |
formulanıń shep hám oń táreplerin salıstirsa3. |
|
T2/T1 = Q2/Q1 |
(9) |
kelip shıǵadı. Demek T1 hám T2 temperaturali eki dene temperaturasın salıstırıw ushın olarda Karno tsiklın ámelge asırıw kerek. Bunda bir dene suwıtqısh, ekinshisi ısıtqısh rolin oynaydı. (9) formuladan kórinip tur, deneler temperaturalarınıń qatnası suwıtqıshǵa berilgen jıllılíq muǵdarınıń ısıtqıshdan alınǵan jıllılíq muǵdarına qatnasına te4. Bunday jol menen anıqlanǵan temperatura, termometrnıń jumısshı zatınıń turine baylanıslı emes.
4. ENTROPIYA. İDEAL GAZ ENTROPIYASI.
Karno tsiklinıń p.j.k.sı |
Q1 Q2 |
|
T1 T2 |
formulasınan |
|
|
|||
|
Q1 |
|
T1 |
|
|
|
88 |
|
|

Q1/T1 Q2/T2 = 0 ekenligi kelip shıǵadı. Bunda Qǵ jumısshı deneniń suwıtqıshǵa bergen jıllılíq muǵdarı, sonıń ushın ol teris. Bunı esapqa alsaq, joqarıdagi ańlatpa
Q1/T1 + Q2/T2 = 0 (10) kórinisin aladı. Bunda Q/T qatnasına keltirilgen jıllılíq muǵdarı dep ataladı. Demek, Karno tsikli ushın keltirilgen jıllılíq muǵdarlarınıń summası nolge te4. Anıq teoriyalíq esaplawlar sonı kórsetedi, hár qanday qaytımlı protsessler ushın keltirilgen jıllılíq muǵdarlarınıń summası nolge te4. Sonıń ushın (10) formulanı ulıwma jaǵdayda
|
dQ |
0 |
(11) |
T |
|||
kórinisinde jazıw mumkin. |
|
|
|
Tuyıq kontur boyínsha alınǵan integraldıń |
nolge teńliginen integral astındaǵı ańlatpa |
||
sistema halatın belgilaytuǵın qandayda funktsiyanıń tolíq differentsialı bolıp, ol tek sistema halatı menen anıqlanıp, sistemanıń bul halatga qanday jollar menen kelgenine baylanıslı emes.
dQ/T - differentsial sistemanıń halat funktsiyasi yaki entropiya dep ataladı hám S penen
belgilenedi. |
|
Qaytımlı protsessler ushın entropiyanıń ózgerisi nolge te4. |
|
S = 0 |
(12) |
Qaytımsız protsess waqıtida sistemanıń entropiyasi barlíq waqıt artadı. |
|
S > 0 |
(13) |
Joqarıdaǵı (12) hám (13) formulalar tek tuyıq sistemalar ushın ǵana tuwrı bolıp tabıladı. Eger sistema sırtqı ortalíq penen jıllılíq almasıp atırǵan bolsa, onıń entropiyasi turliche bolıwı
mumkin. (12) hám (13) qatnasın biriktirip |
|
S 0 |
(14) |
kórinisinde jazıw mumkin.
(14) ańlatpaǵa Klazius teńsizligi dep ataladı. (14) dan kórinip tur, tuyıq sistemada entropiya ósiwi (qaytımsız protsesslerde) yaki turaqlı qalıwı mumkin (qaytımlı protsesslerde).
Eger sistema teńsalmaqlı I-halatdan 2-halatǵa ótip atırǵan bolsa, entropiyanıń ózgerisi (11) ne kóre
|
|
|
|
|
|
|
2 |
dQ |
|
2 |
dU d |
|
S |
1 2 |
S |
2 |
S |
1 |
|
|
T |
|
|
Т |
(15) |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
boladı.
İdeal gaz ushın entropiyanıń ózgerisin kóreyik. Bizge belgili, dU m CV dT
d m R T dV |
|
|
V |
bolǵanı ushın entropiyanıń ózgerisi (15) formulaǵa kóre
S |
|
S |
|
S |
|
|
m |
C |
T2 dT |
|
m |
RV2 |
dV |
, |
|
1 2 |
2 |
1 |
|
v |
|
|
|
||||||||
|
|
|
|
|
|
|
V V |
||||||||
|
|
|
|
|
|
|
T T |
|
|||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
yaki
89

S |
|
S |
|
S |
|
|
m |
|
|
T |
2 |
R l n |
V |
2 |
|
|
|
|
|
|
|
C |
|
l n |
|
|
|
(16) |
|||||||
1 2 |
2 |
1 |
|
V |
|
|
|
|
|||||||||
|
|
|
|
M |
|
T2 |
|
V1 |
|
||||||||
boladı.
İdeal gazda entropiyanıń ózgerisi onıń I-halatdan ǵ-halatǵa qanday protsessler arqalı ótiwine baylanıslı emes.
Adiabatik protsess waqıtida entropiya ózgermeydi S = 0, sebebi dQ = 0. Sonıń ushın adiabatik protsessti izoentropik protsess dep te ataydı. (16) formulaǵa kóre izotermik protsesste (T1 = T2)
S m R l nV2
V1
izoxorik protsesste (V1 = V2)
S m C v l n T2
T1
boladı.
Real protsesslerler qaytımsız bolǵani ushın tuyıq sistemadaǵı protsessler entropiyanı asırıwǵa alıp keledi dep aytıw mumkin.
Bunı entropiyanıń ósiw printsipi dep hám aytadı. Bul printsipten TDnıń basqa táriypi kelip shıǵadı:
Makroskopik sistemalarda tek entropiyanı asırıwǵa alıp keletuǵın protsessler bolıwı mumkin.
Bazı jaǵdaylarda sistemanıń házirgi halatı ushın entropiyanıń muǵdarın biliw talap qılınadı. Bunday jaǵdaylarda TDnıń úshinchi bas nızamı dep atalıwshı Nernst teoremasınan paydalanıladı. Bul teorema boyínsha, hár qanday deneniń absolyut temperaturası nolge jaqınlasǵanda onıń entropiyası hám nolge aylanadı.
lim S 0
T 0
Sonıń ushın málim temperaturada sistema entropiyasın esaplawda tómengi shegara sıpatında T = 0 K daǵı halat alınadı.
Bekkemlew ushın sorawlar:
1.Qaytımlı, qaytımsız hám aylanba protsessler degende neni túsinesiz?
2.Sistemanıń halatı hám faza túsiniklarınıń mánisin túsindiriń.
3.Jıllılíq hám suwıtqısh mashinaları arasında qanday parıq bar?
4.Jıllılíq mashinalarınıń hám Karno tsikilini p.j.k.sı qanday esaplanadı?
5.Sistema entropiyası degende neni túsinesiz hám ol qanday esaplanadı?
6.Entropiyanıń statistik mánisin túsindirip beriń.
7. Termodinamikanıń ǵ-nızamına entropiya arqalı qanday táriyp beriledi? 8. Termodinamikanıń q-nızamı ne dep ataladı?
9.İdeal gaz entropiyasi qanday esaplanadı?
10.Karno Tsikli qanday protsesslerden ibarat?
90
13-tema. Real gazlar
Jobası:
1.Molekulalar ara tásir kúshleri hám potentsial energiyası.
2.Van-der-vals teńlemesi.
3.Van-der-vals izotermalari hám olardıń talqılanıwı. Eksprimental izotermalar.
4.Real gazdıń ishki energiyası.
Tayanısh sózler hám túsinikler: İdeal gaz, molekulalarara tásir kúshleri hám potentsial energiyası, real gaz, Van-der-valsteńlemesi, Van-der-vals izotermalari, eksperimental izotermalar, real gazdıń ishki energiyası, Joul-Tomson effekti.
1. MOLEKULALARARA TÁSIR KÚSHLERI HÁM POTENTSIAL ENERGIYASI
Molekula-kinetikalíq teoriyadaǵı ideal gaz modeli haqıyqıy bar gazlardıń siyreklesgen jaǵdayı ushın, joqarı temperaturalar hám tómen basımlar ushın orınlı. İdeal gaz halatı teńlemesin shıǵarıwda molekulalardıń ólshemleri hám ózara tásiri itibarǵa alınbaydı. Basımnıń artıwı molekulalar arasındaǵı aralíqtı kemeytiredi, sonıń ushın molekulalardıń kólemi hám ózara tásirin itibarǵa alıw kerek boladı. Mısal ushın, normal sharayatda ámq gazda 2,69 10 25 molekula bolıp, ol a10 – 4 m3 kólemdi (r 10 6 m) iyeleydi. Bul kólemniń gaz kólemine (1m3) qatnasın itibarǵa almasa da boladı. 500 MPa basımda molekulalar kólemi gaz kóleminiń yarımın quraydı.
Sonday etip joqarı basım hám tómen temperaturalarda ideal gaz modelin qollap bolmaydı. |
|
||||||
|
|
|
Real |
gazlardı |
úyrengenimizde |
biz |
álbette |
F |
|
П |
molekulalarara |
tásirdi |
itibarǵa alıwimiz |
kerek. Bunday |
|
|
Fи т |
|
|||||
|
|
|
|||||
|
а). |
б). |
tásirler 10 9 m aralíqlarta bayqaladı hám aralíq |
|
|||
|
|
|
artıwı |
||||
|
10-9 |
10-9 |
|
|
|
|
|
|
|
r0 |
menen tezde kemeyedi. Molekulalar arasında bir waqıttıń |
||||
r0 |
r, м |
r, м |
|||||
|
Пmin |
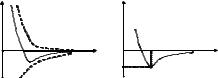
ózinde tartısıw hám iterisiw kúshleri boladı. 1(a)-súwrette |
|
Fт |
|||
|
|||
|
1-suwret |
||
|
|||
|
|
||
|
|
ózara tásirdiń grafigi keltirilgen, Fit –iterisiw kúshleri, Ft – |
tartısıw kúshleri, F - olardıń teń tásir etiwchisi. İterisiw kúshleri oń, tartılısıw kúshleri teris dep esaplanadı. r = r0 aralíqda F = 0, yaǵnıy iterisiw hám tartılısıw kúshleri bir-birin kompensatsiyalaydi. r < r0 de iterisiw kúshleri, r > r0 de tartılısıw kúshleri payda boladı. r > 10 9 m larda molekulalarara ózara tásir kúshleri y kósherde (F = 0). 1(b)-súwrette ózara tásir potentsial energiyasınıń grafigi keltirilgen. Bul grafikten kórinip turıptı, r = r0 aralíqta, yaǵnıy
iterisiw hám tartılısıw kúshleri bir - birin kompensatsiyalaǵanda, yaǵnıy sistema |
turaqlı |
||||||
teńsalmaq halatda bolǵanda, onıń potentsial energiyası minimumǵa erisedi. |
|
||||||
Tartılısıw hám iterisiw kúshleri elektromagnit tabiatǵa iye. Tartılısıw kúshleri |
|
||||||
Ftart |
- |
А |
|
(1) |
|||
r7 |
|||||||
|
|
|
|
|
|||
İterisiw kúshleri |
|
|
|
|
|
|
|
Fiter |
|
B |
|
(2) |
|||
|
r9 |
||||||
|
|
|
|||||
hám potentsial energiya
91
