
Fizika pani boyinsha lekciyalar
.pdf
|
Re |
|
(7.14) |
|
|
|
|
||
|
|
|||
|
|
|
||
ólshemsiz shamaǵa baylanıslılıǵı anıqlangan. |
|
|
|
|
Bunda - suyıqlíq tıǵızlıǵı, |
- nay kesimi boyínsha |
suyıqlíq aǵımınıń ortasha tezligi, - |
||
suyıqlíqtıń jabısqaqlıǵı, -nay kesiminiń ólshemi.
(7.14)-degi hám lardıń qatnasın kinematik jabısqaqlíq dep atalatuǵın = / shama
menen almastırsaq, tómendegi kóriniske keledi: |
|
Re = / |
(7.15) |
Kinematik jabısqaqlíq (mǵ/s) birligi menen ólshenedi. 1 mǵ/s - tıǵızlıǵı á kg/mq hám dinamik jabısqaqlıǵı 1 Pa s bolǵan suyıqlíqtıń kinematik jabısqaqlıǵı bolıp tabıladı. Tájriybelerdiń kórsetiwinshe, ápiwayı sharayatlarda tsilindr sıyaqlı naylar arqalı suyıqlíqtıń aǵımı laminar xarakterge iye bolıwı ushın Re < ǵq00, turbulent aǵım bolıwı ushın bolsa Re > 2300 bolıwı lazım.
Qattı dene hám suyıqlíqtıń ózara tásirlesiwinde payda bolıwshı kúshler qozǵalmaytuǵın suyıqlíq ishinde qattı dene qozǵalǵanda yaki qozǵalıwzshı suyıqlíq ishinde qattı dene tınısh turǵan jaǵdaylarında birdey boladı.
Qattı dene suyıqlíqta qozǵalǵanda qarsılíqqa ushraydı. Suyıqlíq tárepinen denege tásir etiwshi kúsh, ulıwma halda, qozǵalıs baǵıtı menen bazı bir múyesh payda etedi. Tájriybelerdiń kórsetiwinshe, bul kúsh eki kúshtiń jıyındısıdan ibarat (súwret– w):
1) qozǵalısqa qarsılíq kórsetiwshi kúsh suyıqlíq aǵımı boylap baǵıtlanǵan, onı mańlay qarsılíq kúshi (Fl) dep ataydı.
2) Suyıqlíqtıń aǵımına perpendikulyar baǵıtta tásir etetuǵın kúsh, ol kóteriwshi kúsh (Fk) dep ataladı.
Bul kúshlerdiń payda bolıwı hám tábiyati menen tansıayı3. Tekseriwlerden anıqlanıwınsha, bul kúshler qattı denege tiyip turǵan suyıqlíq qatlamında (shegaralíq qatlamda) payda boladı. Shegaralíq qatlam degende suyıqlíqtıń sonday qatlamı túsiniledi, ondaǵı suyıqlíq bóleksheleriniń tezligi nolden suyıqlíq aǵım tezligine teń bolǵan mániske shekem ózgeredi. Shegaralíq qatlamda suyıqlíqtıń jabısqaqlıǵı nátiyjesinde tezlik gradienti bar. Shegaralíq qatlam qalıńlıǵı tájriybelerden
|
|
(7.16) |
 Re
Re
ańlatpası járdeminde anıqlanıwı múmkin.
Bunda: - deneniń xarakterli ólshemi. Re - Reynolds sanı.
Suyıqlíq hám deneniń, bir-birine salıstırǵanda tezligi onsha úlken bolmaǵan jaǵdaylarda qozǵalısqa qarsılíq kúshi suyıqlíqtıń jabısqaqlıǵı menen baylanıslı. Egerde suyıqlíqtıń jabısqaqlıǵı, deneniń forması, ólshemleri jánede deneniń suyıqlíq aǵımı baǵıtına salıstırǵanda
jaylasıwın esapqa alıwshı Sx koeffitsentinen paydalansaq |
|
Fsúyk = Sx |
(7.17) |
ańlatpası orınlı boladı.
52

Fk
F
V
Fp
7- сур ет
Reynolds sanınıń mánisi birga jaqın bolǵanda shegaralíq qatlam qalıńlıǵı dene ólshemi menen salıstıratuǵın dárejede Re<á bolsa, shegaralíq qatlam aǵımnıń derlik barlíq oblastın iyeleydi. Bunday jaǵday ushın r radiuslı shar formadaǵı deneniń qozǵalısına suyıqlíq tárepinen bolatuǵın qarsılíq kúshi súykelis kúshinen ibarat boladı hám ol
= úr
(7.18) ańlatpa menen anıqlanadı. (7.11)-ańlatpa Stoks (áhá9 - 190q) inglis fizik alımı) formulası
dep ataladı.
Bekkemlew ushın sorawlar:
1.Qanday suyıqlíqqa ideal suyıqlíq delinedi?
2.Qısılmaytuǵın suyıqlíq ushın úzliksizlik teńlemesin jazıń hám aytıp beriń? 3.Bernulli teńlemesin jazıń hám teńlemeni qurawshı bóleklerin túsindirip beriń?
4.Jabısqaqlíq kúshi qanday bolıp ótedi?
5.Jabısqaqlíq koeffitsientine anıqlama beriń.
6.Nyuton formulasın túsindirip beriń.
7.Kinematik jabısqaqlíq neni ańlatadı?
9-tema. Mexanikalíq terbelisler hám tolqınlar
Jobası:
1.Mexanikalíq garmonik terbelisler teńlemesi
2.Mayatnikler
3.Birdey baǵıttaǵı terbelislerdi qosıw
4.Garmonikalíq terbelisler energiyası
5.Sóniwshi hám májbúriy terbelisler. Rezonans
6.Tolqınlı protsessler
Tayanısh sóz hám túsinikler: terbelmeli qozǵalıs, garmonikalíq terbelis, terbelis amplitudası, jiyiligi, periodı, prujinalı mayatnik, matematikalíq mayatnik, fizikalíq mayatnik, terbelislerdi qosıw, garmonikalíq terbelisler energiyası, sóniwshi hám májbúriy terbelisler, rezonans, tolqınlı protsessler, kóldeneń hám boylama tolqınlar
1. Mexanikalíq garmonik terbelisler teńlemesi
Bazı bir materiallíq tochkanıń teńsalmaqlíq halatınan dáslep bir tárepge, soń ekinshi tárepge periodlíq tákirarlanıwshı qozǵalısı terbelmeli qozǵalıs dep ataladı. Qozǵalıstıń bul túrin
53

biz tabiyatta, texnikada júdá kóp ushratamız. Máselen, saat mayatniginiń, telefonlardıń membranaları terbelisleri, puw dvigatelleri hám ishten janıw dvigatelleriniń porshenleri qozǵalısların aytıwımız múmkin. Terbelislerdiń eń ápiwayı túri garmonikalíq terbelisler. Deneniń qozǵalıs traektoriyasınıń waqıt boyínsha ózgerisi sinus yaki kosinuslar nızamı boyınsha ózgeretuǵın terbelislerge garmonikalíq terbelisler delinedi.
|
х А sin( t ) |
|
yaki |
x A cos( t ) |
(1) |
|
|
Bunda x – deneniń awısıwı, A – deneniń teńsalmaqlíq jaǵdayınan maksimal awısıwı bolıp, onı terbelis amplitudası dep ataydı. Sinus yaki kosinustıń eń úlken mánisi birge teń bolǵanı ushın Xmaks=A boladı ; (t+ ) – garmonikalíq terbelistiń fazası,
|
- terbelistiń dáslepki fazası dep ataladı; |
|
2 |
berilgen |
||||||||
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
Т |
||
|
terbelis ushın turaqlı bolıp, garmonikalíq terbelistiń tsikllíq |
|||||||||||
1–с67рет |
jiyiligi delinedi. =0 bolǵan jaǵday ushın (1) teńleme menen |
|||||||||||
ańlatılǵan |
garmonikalíq |
terbelisler |
grafigi |
1–súwrette |
||||||||
|
||||||||||||
|
kórsetilgen. |
|
|
|
|
|
|
|
|
|
|
|
Terbelmeli qozǵalıstaǵı deneniń teńsalmaqlíq jaǵdayınan eń shetke shıǵıwı awısıw dep |
||||||||||||
ataladı. Deneniń bir tolíq terbelisi ámelge asıwı ushın ketken waqıt period (T) dep ataladı. |
||||||||||||
Terbeliwshi dene bir period ishinde tórt amplitudaǵa teń bolǵan joldı basıp ótedi. Eger t |
||||||||||||
waqıtta dene n márte terbeletuǵın bolsa, onıń periodı |
|
|
|
|
|
|
||||||
|
Т |
|
t |
(s) |
|
|
|
|
(2) |
|||
|
|
n |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||
ǵa teń boladı. Birlik waqıt dawamındaǵı terbelisler sanı |
|
|
|
|
||||||||
|
|
1 |
|
|
1 |
1Gts |
|
|
|
|
||
|
|
|
|
|
|
|
|
(3 ) |
||||
|
|
|
|
|
|
|||||||
|
|
T |
s |
|
|
|
|
|
||||
jiyilik dep ataladı. Sİ da period sekundlarda, jiyilik bolsa Gertslarda ólshenedi. Tsikllíq
hám sızıqlı jiyilikler arasında tómendegishe baylanıs bar: |
|
2 |
(4) |
bunda 2 sekund ishindegi terbelisler sanın ańlatadı.
Terbeliwshi denege tásir etiwshi kúsh awısıwǵa proportsional, biraq kúsh awısıwǵa keri
baǵıtlanǵan: |
|
F k х |
(5) |
(5) ańlatpa terbelmeli qozǵalıs ushın Guk nızamı deb aytıladı. Bunda |
k – prujinanıń |
qattılıǵı delinedi. Nyutonnıń ekinshi nızamınan paydalansaq (5) tómendegi kóriniste jazıladı: |
|
||||||||||
|
|
|
|
|
|
m a k х |
(6) |
||||
Bundaǵı a = |
d 2 x |
teń ekenligin itibarǵa alsaq, (6) ańlatpa tómendegi kóriniske keledi: |
|
||||||||
dt 2 |
|
||||||||||
|
|
m |
d 2 x |
kX |
yaki |
|
d 2 x |
|
k |
x 0 |
(7) |
|
|
|
|
dt 2 |
|
||||||
|
|
|
dt2 |
|
|
|
m |
|
|||
Bunda k hám m oń shamalar bolǵanlıǵı ushın
54

|
k |
02 |
|
(8) |
||
|
|
|
|
|||
|
m |
|
|
|||
dep belgilesek (7) ańlatpa |
|
|
||||
|
|
d 2 x |
|
02 x 0 |
(9) |
|
|
|
|
||||
|
|
dt2 |
|
|
||
kórinisti aladı. (9) ańlatpa ekinshi tártipli differentsial teńleme bolıp, onıń shechimi |
|
|||||
|
|
|
|
|
x Acos( 0t ) |
(10) |
kóriniste boladı. Bul ańlatpa (1) teńlemenıń ózi, bunda A – amplituda, x |
– awısıw, |
|||||
0t - terbelis fazası, - bolsa dáslepki fazası.
Demek, joqarıda bayan etilgen pikirlerimizdi ulıwmalastırıp, garmonikalíq terbeliske jáne bir tómendegi anıqlamanı beriw orınlı boladı: Deneniń awısıwǵa proportsional, teńsalmaqlíq jaǵdayına qaray baǵıtlanǵan kúsh tásirindegi terbelisleri garmonikalíq terbelisler dep ataladı.
(10)-daǵı 0 -terbelistiń menshikli tsikllíq jiyiligi dep ataladı. Menshikli terbelis periodı
(T0 ) menen 0 dıń qatnası tómendegishe ańlatıladı:
0 |
|
2 |
(11) |
|
0 |
||||
|
|
|
2. Mayatnikler
Teńsalmaqlíq jaǵdayı dógereginde terbelmeli qozǵalıstaǵı qattı dene mayatnik dep ataladı. Prujinalı, matematikalíq hám fizikalíq mayatniklerdiń terbelis nızamlılíqları menen tanısıp óteyik.
|
|
|
1. Prujinalı mayatnik. Prujinaǵa asılǵan m–massalı |
||
|
|
|
shardan ibarat sistemanı qarap óteyik (2–súwret). Teńsalmaqlíq |
||
|
|
|
jaǵdayında mg awırlíq kúshi Fs serippelik (Fs=- kx) kúshi |
||
|
|
|
menen teńlesedi. Sırttan tásir bolmaǵansha mayatnik óziniń |
||
|
|
|
teńsalmaqlíq jaǵdayın saqlay |
beredi. Eger shardı tómenge |
|
|
|
|
x 0 aralíqqa tartıp onı teńsalmaqlíq jaǵdayınan shıǵarsaq (2b |
||
a) |
b) |
c) |
– súwret), júktiń awırlíq kúshi prujinanıń serippelik kúshinen |
||
|
|
|
|||
|
2–с67рет |
|
kishi bolıp qaladı, Fs kúshi bolsa teńsalmaqlíq jaǵdayına qaray |
||
|
|
baǵıtlanǵan boladı Fs 0 . |
|
|
|
|
|
|
Shar |
teńsalmaqlíq jaǵdayına |
|
jetkennen, inertsiya sebepli qozǵalısın dawam ettiredi, nátiyjede |
x 0 |
bolǵanda kúsh Fs 0 |
|||
boladı, (2c–súwret) prujina qısıladı. Bul jaǵdayda júkke tásir etiwshi juwmaqlawshı kúsh, jáne teńsalmaqlíq jaǵdayına qaray baǵıtlanǵan boladı. Usı tárizde teńsalmaqlíq jaǵdayınan shıǵarılǵan prujinalı mayatniktiń terbelisleri ámelge asadı. (8) hám (11) ańlatpalardan paydalanıp prujinalı mayatniktiń terbelis periodı ushın
Tn 2 |
m |
(12) |
|
|
|||
k |
|||
|
|
formulanı payda etemiz.
55

2. Matematikalíq mayatnik. Sozılmaytuǵın salmaqsız jipke asılǵan awırlíq kúshi tásirinde vertikal tekisliktegi sheńber doǵası boylap terbele alatuǵın materiallíq tochka
matematikalíq |
mayatnik dep ataladı (3-súwret). |
|
||||
|
|
|
Mayatnik |
jibi vertikal jaǵdayda bolsa, sharǵa tásir etiwshi |
||
|
|
|
awırlíq kúshi |
|
mg jiptiń keriliw kúshi FR menen |
teńlesedi. |
|
|
|
Biraq mayatnikti teńsalmaqlíq jaǵdayınan bazı bir |
múyeshke |
||
|
|
|
awıstırǵanda awırlíq kúshi mg hám jiptiń keriliw kúshi FR bir |
|||
|
|
|
tuwrı sızıqta |
jatpaydı. Nátijede olardıń teń tásir etiwshi kúshi |
||
|
|
|
F mg FR |
payda boladı. Mayatnik oń tárepke awısqan halda |
||
a) |
b) |
c) |
(3b–súwret) F shep tárepke baǵıtlanǵan, mayatnik shep tárepke |
|||
|
|
|
||||
3–súwret |
|
awısqan halda (3v-súwret) F oń tárepke baǵıtlanǵan boladı. |
||||
|
|
|
||||
Demek, |
|
|
|
|
|
|
|
|
|
|
|
F mg Sin |
(13) |
Bul kúsh tásirinde shar l radiuslı sheńber doǵası boylap teńsalmaqlíq jaǵdayına qaray qozǵaladı. Mayatniktiń bul qozǵalısı aylanbalı qozǵalıs dinamikasınıń tiykarǵı teńlemesi
I |
(14) |
menen xarakterlenedi. Bunda I – shardıń aylanıw kósherine salıstırǵanda inertsiya momenti, – onıń múyeshlik tezleniwi, M bolsa F kúshtiń O kósherge salıstırǵandaǵı momenti bolǵanı ushın
I ml2 , d 2 , M mg l sin dt2
ańlatpalarınan paydalanıp (14) ni tómendegi kóriniste jazıw múmkin:
ml 2 |
d 2 |
mgl sin |
ёки |
d 2 |
|
g |
sin 0 |
(15) |
dt2 |
dt2 |
|
||||||
|
|
|
|
l |
|
|||
múyesh kishi bolǵanda. Sin di menen almasıtırıw múmkin. Nátiyjede (15) ańlatpa
d 2 g 0 dt2 l
kóriniske keledi:
gl 02
belgilew kiritsek:
d 2 2 0 dt2 0
teńlemeni payda etemiz. Bul teńlemeniń sheshimi
m cos( t )
kóriniste boladı. (18) den paydalanıp matematikalíq mayatnik terbelis periodı
T |
2 |
2 |
|
l |
|
|
|
|
|||
M |
0 |
|
|
g |
|
|
|
|
|
(16)
(17)
(18)
(19)
formula menen anıqlanǵanın tabamız.
Demek, kishi awısıw múyeshlerinde matematikalíq mayatniktiń terbelis periodı mayatnik uzınlıǵınıń kvadrat korenine tuwrı proportsional, erkin túsiw tezleniwiniń kvadrat korenine keri
56

proportsional bolıp, mayatnik terbelisleriniń amplitudasına hám massasına baylanıslı emes.
Sonday-aq, matematikalíq mayatniktiń terbelis tegisligi ózgerissiz qaladı.
3. Fizikalíq mayatnik – degende inertsiya orayínan ótpeytuǵın gorizontal qozǵalmaytuǵın aylanıw kósheri dógereginde awırlíq kúshi tásirinde qozǵalısta bolatuǵın qattı dene túsiniledi. Aylanıw kósheri fizikalíq mayatniktiń asılıw kósheri dep ataladı. Fizikalíq mayatniktiń inertsiya orayínan (S) asılıw kósherine ótkerilgen perpendikulyar (OS) vertikal sızıq penen sáykes túsken halda mayatnik teńsalmaqlíq jaǵdayında boladı (4a-suwret).
Teńsalmaqlíq jaǵdayınan bazı bir múyeshke awıstırılǵanda (4b yaki 4c–súwret) m g hám FR kúshlerdiń teń tásir etiwshisi fizikalíq mayatniktiń teńsalmaqlíq jaǵdayına qaray qaytarıwǵa
umıtılıwshı F kúshi boladı. Fizik mayatniktiń qozǵalısı ushın aylanba qozǵalıs dinamikasınıń tiykarǵı teńlemesi
a) |
b) |
c) |
|
d 2 |
|
|
I |
|
mgh sin |
(20) |
|||
|
4–súwret. |
dt2 |
||||
|
|
|
|
|
||
formada jazıladı. Bunda I – fizikalíq mayatniktiń asılıw kósherine salıstırǵanda inertsiya momenti, m-massası, h – bolsa fizikalíq mayatniktiń asılıw kósheri hám inertsiya orayí arasındaǵı aralı3. Kishi terbelisler ushın sin ekenligin esapqa alsaq, (20)-ańlatpa tómendegishe jazıladı:
|
d 2 |
|
mgh |
0 |
|
||||||||||||||
|
dt2 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|||||
|
|
d 2 |
02 0 |
(21) |
|||||||||||||||
|
|
dt2 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
2 |
|
mgh |
|
|
|
(22) |
||||||||
|
|
|
|
0 |
|
I |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
dep belgilemeymiz. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Solay etip, fizikalíq mayatniktiń terbelis periodı |
|
||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||
T |
|
|
2 |
|
|
|
I |
(23) |
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
mgh |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
formula menen anıqlanadı. (19) hám (23) lerdi salıstırıp |
|
||||||||||||||||||
|
|
|
|
l |
|
|
|
|
I |
|
|
|
|
|
|
(24) |
|||
|
|
|
|
k |
|
mh |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
fizikalíq mayatniktiń keltirilgen uzınlıǵın (lk ) |
|
tabamız. Solay etip, fizikalíq |
mayatniktiń |
||||||||||||||||
keltirilgen uzınlıǵı sonday matematikalíq mayatniktiń uzınlıǵınan ibarat, bul mayatniktiń terbelis periodı berilgen fizikalíq mayatniktiń terbelis periodına teń boladı.
(12), (19) hám (23) ańlatpalar tiykarında tómendegi juwmaqqa kelemiz: prujinalı mayatnik, matematikalíq hám fizikalíq mayatnikler ushın ulıwma qásiyet sonnan ibarat, mayatniklerdiń kishi terbelislerinde, yaǵnıy garmonikalíq terbelisler bolıp atırǵanda terbelis periodı, amplitudaǵa baylanıslı emes. Mayatniklerdiń bul qásiyeti izoxronlíq dep ataladı. Bul kórip ótilgen mayatnikler texnikanıń turli tarawlarında qollanıladı.
3. Birdey baǵıttaǵı terbelislerdi qosıw
57
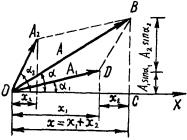
Baǵıtları hám jiyilikleri birdey, biraq amplituda hám dáslepki fazaları hár qıylı bolǵan eki garmonikalíq terbelislerdiń qosılıwın qarap óteyik. Terbeliwshi deneniń x awısıwı tómendegi xá hám xǵ awısıwlardıń jıyındısınan ibarat boladı:
х1 |
А1 cos( 0t 1 ) |
(25) |
|
x2 A2 cos( 0t 2 ) |
|||
|
|||
Bul terbelislerdi qosıwda amplitudalardıń vektorlar diagrammasınan paydalanamız. Vektorlardıń qosıw qaǵıydasına muwapıq juwmaqlawshı A vektordı sızayı3. Bul vektordıń x kósherine proektsiyası, qosılıwshı vektorlar proektsiyalarınıń jıyındısına teń, yaǵnıy
х х1 х2
ekenliginin 5-súwretten kóriwge boladı. |
|
|
|
|
|
|
|
|
|
|
|
|||
Demek, А vektor juwmaqlawshı terbelis amplitudası. Bul vektorda |
А1 hám А2 vektorlar |
|||||||||||||
sıyaqlı 0 múyeshlik tezlik penen aylanadı. |
|
|
|
|
|
|
|
|
|
|||||
А nıń mánisin bolsa kosinuslar teoremasınan paydalanıp tabıw múmkin. |
|
|
|
|
||||||||||
А2 А2 |
А2 |
2А А cos |
|
A2 |
A2 |
2A A cos( |
|
) |
(26) |
|||||
1 |
2 |
1 |
2 |
2 |
|
1 |
1 |
2 |
1 |
2 |
2 |
|
1 |
|
|
|
|
||||||||||||
nıń mánisin OVS úshmúyeshlikten anıqlaymız:
|
|
BC |
A1 sin1 A2 sin2 |
|
||||
|
tg |
|
|
|
|
(27) |
||
|
OC |
A cos A cos |
2 |
|||||
|
|
|
|
1 |
1 |
2 |
|
|
|
Solay etip, garmonikalíq terbelislerdi vektorlar járdeminde |
|||||||
|
súwretlew usulı, bir neche terbelislerdi qosıwdı, vektorlardıń |
|||||||
|
qosıw qaǵıydasına keltiriwge imkan beredi eken. Demek, |
|||||||
|
juwmaqlawshı terbelmeli qozǵalısta 0 |
jiyilik penen qosılıwshı |
||||||
5 – súwret. |
terbelisler baǵıtında ámelge asıwshı garmonikalíq terbelis boladı, |
|||||||
onıń teńlemesi |
|
|
|
|
|
|||
|
|
|
|
|
|
|||
|
|
x A cos( 0t ) |
|
(28) |
||||
bolıp, A hám nıń mánisleri (26) hám (27) ańlatpalar menen anıqlanadı. |
|
|||||||
4. Garmonikalíq terbelisler energiyası
Biz joqarıda mayatniklerdiń terbelis protsessinde olardıń kinetikalíq energiyası potentsial energiyaǵa hám kerisinshe, potentsiallíq energiya bolsa kinetikalíq energiyaǵa aylanıp turıwına itibar bermedik. Endi garmonikalíq terbelisler energiyasın anıqlayı3. Massası m bolǵan materialíq tochka serippelik kúshi tásirinde garmonikalíq terbelmeli qozǵalıs jasaydı.
|
F kx |
||
Qozǵalıs dawamında materiallíq tochka málim bir tezlikke erisedi, demek ol málim |
|||
kinetikalíq energiyaǵa iye boladı. |
|
|
|
W |
|
1 |
m 2 |
|
|
||
k |
2 |
|
|
|
|
||
Biraq garmonikalíq terbelmeli qozǵalıstaǵı materiallíq tochkanıń tezligi ushın
58

|
dx |
|
d |
A cos( |
|
t ) A |
|
sin( |
|
t ) |
(29) |
|
|
0 |
0 |
0 |
|||||||
|
dt |
dt |
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||
ańlatpa payda boladı. Ol jaǵdayda kinetikalíq energiya formulası:
|
W |
|
1 |
m 2 A2 sin2 ( |
|
t ) |
|
(30) |
|||||
|
|
0 |
|
||||||||||
|
|
k |
2 |
0 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
kóriniste jazıladı. |
|
|
|
|
|
|
|
|
|
|
|
||
Potentsial energiya mánisi bolsa |
|
|
|
|
|
|
|
|
|
|
|
||
х |
|
|
|
|
x |
1 |
kx2 |
|
|
1 |
kA2 cos2 ( |
|
|
Wп |
F |
dx |
|
kx dx |
|
|
0t ) |
(31) |
|||||
2 |
|
2 |
|||||||||||
0 |
|
|
|
|
0 |
|
|
|
|
|
|
||
(30) hám (31) ańlatpalarındaǵı sinus hám kosinustıń maksimal mánisi 1 ge te4. Sonıń ushın kinetikalíq hám potentsiallíq energiyalardıń maksimal mánisleri tómendegishe:
W |
|
1 |
m 2 A2 |
, |
(32) |
||
|
|||||||
k |
|
2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Wп |
1 |
kA2 |
(33) |
|
|
|
|
|
||||
|
|
|
2 |
|
|
|
|
Garmonikalíq terbelmeli qozǵalıstaǵı materiallíq tochkanıń qálegen jaǵdaydaǵı tolíq energiyası kinetikalíq hám potentsiallíq energiyalarınıń jıyındısınan ibarat:
W Wk WП 12 m 02 A2 sin2 (0t ) 12 kA2 cos2 (0t ) k m 02 teń ekenligine esapqa alsaq tolíq energiya ushın
W |
1 |
m 02 A2 |
yaki |
W |
1 |
kA2 |
(34) |
|
2 |
2 |
|||||||
|
|
|
|
|
|
formulanı payda etemiz.
Bunı (32) hám (33) menen salıstırıp, tómendegi juwmaqqa kelamiz: terbeliwshi sistemanıń qálegen jaǵdaydaǵı tolíq energiyası ózgermeydi hám ol kinetikalíq yaki potentsial energiyanıń maksimal mánisine teń boladı.
5. Sóniwshi hám májbúriy terbelisler. Rezonans
Sóniwshi terbelisler. Eger mayatnik teńsalmaqlíq jaǵdayınan shıǵarılıp, soń qoyıp jiberilse, onda mayatnik tek ǵana dáslepki berilgen energiya esabınan qanday-da bir waqıt terbelip turadı. Mayatniktiń bunday terbelisleri erkin terbelisler yaki menshikli terbelisler delinedi. Praktikada hawanıń qarsılıǵı hám súykelistiń bolıwı mayatnik terbelisler amplitudasın waqıttıń ótiwi menen kemeyiwine alıp keledi. Waqıttıń ótiwi menen amplitudası kemeyip baratuǵın terbelisler sóniwshi terbelisler dep ataladı.
Kishi tezliklerde hawanıń qarsılíq kúshi tezlikke proportsional, biraq oǵan keri baǵıtlanǵan boladı:
F r r |
dx |
(35) |
k |
dt |
|
|
bunda r – qarsılíq koeffitsienti dep ataladı. |
|
Terbeliwshi dene ushın Nyutonnıń ekinshi nızamınan paydalansaq, nátiyjede sóniwshi |
|
terbelisti xarakterleytuǵın teńleme |
|
59

m |
d 2x |
kx r |
dx |
dt2 |
dt |
kórinisinde jazıladı. Bul teńlemeniń eki tárepin m ǵa bólsek hám
k |
2 |
; |
r |
2 |
|
|
|||
m |
0 |
|
m |
|
|
|
|||
belgilewlerden paydalansaq, tómendegi qatnastı payda etemiz:
d 2x |
2 |
dx |
2x 0 |
dt 2 |
|
||
|
dt |
0 |
Bul teńlemeniń sheshimi 0 bolǵan hal ushın tómendegishe boladı:
x A |
е t cos( |
c |
t ) |
(39) |
0 |
|
|
|
(36)
(37)
(38)
Bundaǵı c - sóniwshi terbelis jiyiligi, onıń mánisi
|
c |
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||
|
0 |
|
|
|
|
|
|
|
|
|
|
(40) |
|||||||
ańlatpa menen anıqlanadı. Tek bir dara jaǵdayda, yaǵnıy |
|
r |
0 |
bolǵanda |
|
|
|
boladı. |
|||||||||||
|
|
c |
0 |
||||||||||||||||
|
|
|
|
|
|
|
|
2m |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Sóniwshi terbelis periodı (Ts) bolsa menshik terbelis periodı (T0) dan úlken: |
|
|
|
|
|||||||||||||||
Tc |
2 |
|
|
|
2 |
T0 |
|
|
2 |
|
|
|
(41) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
2 2 |
0 |
|
|
|
||||||||||||||
|
c |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sóniwshi terbelislerdiń amplitudası bolsa waqıttıń ótiwi menen |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
A A е t |
|
|
|
|
|
|
|
|
|
|
(42) |
||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nızam boyínsha kemeyip baradı (6– súwret). Bunda A0 – baslanǵısh amplituda, bolsa sóniw koeffitsienti dep ataladı.
Amplitudanıń kemeyip barıwı 6 – súwrette punktir sızıq penen kórsetilgen.
Májbúriy terbelisler. Mayatniktiń terbelisleri toqtamawı ushın qorshaǵan ortalíqqa ketip atırǵan energiyanı úzliksiz qayta
tiklep turıw kerek, yaǵnıy mayatnikke periodlı ózgerip turıwshı kúsh penen tásir etip turıw kerek. Periodlı túrde ózgerip turatuǵın bunday sırtqı kúshti májbúr etiwshi kúsh dep ataydı. Materiallíq tochkaǵa garmonikalíq nızam boyínsha ózgeriwshi
F F0 cos t
60

kúsh tásir etsin. Dinamikanıń ekinshi nızamına muwapıq, materiallíq tochkanıń bul jaǵdaydaǵı qozǵalıs teńlemesin tómendegishe jazıwımız múmkin:
m |
d 2 x |
kx r |
dx |
F cos t |
|
|||||||
|
|
|
|
|||||||||
|
dt2 |
|
|
dt |
0 |
|
|
|
||||
|
|
|
|
|
|
|
||||||
yaki |
|
|
|
|
|
|
|
|
|
|||
|
|
d 2 x |
2 |
dx |
|
x |
F |
cos t |
|
|||
|
|
|
|
|
|
0 |
(43) |
|||||
|
|
|
|
|
|
|
||||||
|
|
dt 2 |
|
dt |
0 |
|
m |
|
|
|||
|
|
|
|
|
|
|
|
|||||
(43) teńlemeniń shechimi bolsa májbúr etiwshi kúsh jiyiligi menen bolatuǵın terbelislerdi kórsetedi. Bul terbelislerdi materiallíq tochkanıń májbúriy terbelisleri dep ataydı. (7–súwret)
Materiallíq tochkanıń menshikli terbelisileri májbúr etiwshi kúsh tásir ete baslaǵan dáslepki momentte júzege keledi hám eksponentsial nızam boyínsha sónedi. (43) teńlemeniń sheshimi:
x A cos( t ) |
(44) |
qatnası menen anıqlanadı. Bundaǵı A májbúriy terbelisler amplitudası, onıń mánisin:
A |
|
F0 |
|
(45) |
|
|
|
|
|||
m |
(02 2 )2 4 2 2 |
||||
|
|
|
formula járdeminde esaplaw múmkin. bolsa májbúr etiwshi kúsh hám májbúriy terbelis fazalarınıń ayırması, onıń mánisi:
tg |
|
2 |
(46) |
|
|
|
|||
|
02 2 |
|||
A |
|
formula járdeminde esaplanadı.
Rezonans hádiysesi. Eger =0 bolǵanda, yaǵnıy májbúr etiwshi kúshtiń mánisi ózgermegende (45)- ańlatpadan
A |
F0 |
|
F0 |
(47) |
|
m 02 |
K |
||||
8 – су7рет |
|
|
kelip shıǵadı. bolsa, (45) ge muwapıq, amplituda nolge umtıladı. 8-súwretten kórinip tur,nın bazı bir aralíq mánisinde amplituda maksimal mániske jetedi. Bul hádiyse, yaǵnıy májbúr etiwshi kúsh jiyiliginiń bazı bir anıq mánisinde májbúriy terbelisler amplitudasınıń keskin artıp ketiwi rezonans hádiysesi dep ataladı.
Rezonans hádiysesi júzege kelgen jaǵdaydaǵı májbúr etiwshi kúshtiń jiyiligi rezonans jiyiligi dep, amplitudanıń maksimal mánisi bolsa rezonans amplitudası dep ataladı. Rezonans hádiysesi júzege kelgende (45) ańlatpa maksimal mániske jetedi, biraq bul halda bul ańlatpadaǵı bólshektiń bólimi minimal mániske erisiwi lazım. Sonıń ushın (45) niń bóliminen boyınsha tuwındı alıp, onı nolge teńeymiz:
yaki |
2( 02 |
2 )2 8 2 0 |
|||
( 2 |
2 ) 2 2 |
0 |
|||
|
|||||
|
0 |
|
|
|
|
bunnan |
|
|
|
|
|
|
p |
|
2 |
2 2 |
(48) |
|
|
0 |
|
|
Rezonans jiyiliginiń bul mánisin (ńó) qoysaq, rezonans amplituda mánisin tabamız:
61
