Добавил:

aysultan Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Каракалпакский государственный университет им. Бердаха

Предмет:

Физика

Файл:

Fizika pani boyinsha lekciyalar

.pdf

Скачиваний:

Добавлен:

09.08.2024

Размер:

6.47 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 193 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 > Следующая >>>

bunda: m - sistemasınıń ulıwma massası; xi ,yi ,zi - sistema quramındaǵı i - deneniń koordinataları.

Dara jaǵdayda, eger sistema massaları m1 hám m2 bolǵan eki deneden ibarat bolsa hám olardı X kósheri boyínsha jaylastırsaq, inertsiya orayínıń koordinatası

X c m1x1 m2 x2 m1 m2

boladı. Sistema inertsiya orayín anıqlawshı radius-vektordan (rc) waqıt boyínsha alınǵan tuwındı (rc nıń birlik waqıt dawamında ózgerisi) inertsiya orayínıń tezligin ańlatadı:

Vс	drc	(3.12)
	dt

(3.10) formulanı (3.12) ge qoyıp, inertsiya orayínıń tezligi ushın

d 1

mi ri

miVi

dt m

teńlemege iye bolamız; bunda Vi hám i

sáykes túrde i-deneniń tezligi hám impulsı; Onda

PPi miVi

(3.13)

(3.14)

sistemanıń tolíq impulsı bolıp, kóbinese P-inertsiya orayínıń impulsı dep ataladı; m-sistemasınıń ulıwma massası yaǵnıy:

m m1			m2				... mn		mi .	(3.15)
									i
Endi (3.14)-ni esapqa alıp, (3.13)-ańlatpanı tómendegishe jazamız:
	Vс					yaki P = mVs


			m
Nyutonnıń ekinshi nızamı boyínsha sistemanıń tolíq impulsınan waqıt boyínsha alınǵan
tuwındı usı sistemaǵa tásir etip atırǵan sırtqı kúshlerdiń vektor jıyındısına teń:

	dP	m		dVc			mа
	dP			dVc					F ,	(3.16)
								c	F ,	(3.16)
	dt				dt			c	s
	dt				dt

bunda: s - inertsiya orayínıń tezleniwi,

Fs – sistemaǵa tásir etip atırǵan sırtqı kúshlerdiń vektor jıyındısı.

Tuyıq sistemada oǵan tásir etiwshi sırtqı kúshler joq yaki sırtqı kúshlerdiń teń tásir etiwshisi nolge teń (Ft = 0). Ol halda aqırǵı teńlikten inertsiya orayínıń tezleniwi

аc dVdtc 0

boladı. Bunnan Vs = sonst ekenligi kelip shıǵadı. Bul juwmaq inertsiya orayínıń saqlanıw nızamın ańlatadı hám ol tómendegishe sıpatlanadı: tuyıq sistemanıń inertsiya orayí tuwrı sızıq boylap teń ólshewli qozǵalısta boladı yaki tınısh halatta boladı.

Sistema impulsınıń saqlanıw nızamınan massanıń additivlik nızamı kelip shıǵadı. Sistemanıń massası onıń quramındaǵı denelerdiń massalarınıń jıyındısına te4.

İnertsiya orayí túsinigi bir neshe deneden ibarat bolǵan sistema qozǵalısın sıpatlawda da

bir qansha qolaylılíqlarǵa iye. Usı maqsette (áú) formulanı tómendegishe jazamız:

	dVc
m	dVc	F ,	(3.17)
m		F ,	(3.17)
	dt	T
	dt

Bizge belgili, bunda Vs - inertsiya orayínıń tezligi, Fs - sistemaǵa tásir etip atırǵan barlíq sırtqı kúshlerdiń teń tásir etiwshisi (ishki kúshlerdiń teń tásir etiwshisi nolge teń).

Demek, sistemanıń inertsiya orayínıń alǵan tezleniwi, yaǵnıy dVs/dt sırtqı kúshlerdiń teń tásir etiwshisine tuwra hám sistema quramındaǵı deneler massalarınıń jıyındısına keri proportsional ekenligi kelip shıǵadı.

Bunnan kórinip tur, bul formula forması boyínsha massası m hám tezligi V bolǵan bir materiallíq tochkanıń sırtqı Fs kúsh tásirinde bolıp atırǵan qozǵalısın ańlatıwshı teńlemege uqsas. Sonıń ushın bul formula inertsiya orayínıń qozǵalıs teńlemesin ańlatadı hám ol tómendegi juwmaqqa alıp keledi: sistemanıń inertsiya orayí sırtqı kúshler tásirinde massası sistema quramındaǵı barlíq denelerdiń massasına teń bolǵan materiallíq tochka sıyaqlı qozǵaladı. Bul juwmaq inertsiya orayínıń qozǵalısı haqqındaǵı teorema dep ataladı.

(17)-formuladan kórinip tur, inertsiya orayínıń tezligin ózgertiw ushın sistemaǵa sırtqı kúshler tásir etiwi kerek; sistema quramındaǵı denelerdiń ózara tásiri nátiyjesinde payda bolatuǵın ishki kúshler usı denelerdiń inertsiya orayína salıstırǵanda tezliklerin ózgertsede, bul kúshler inertsiya orayínıń halatın, qozǵalıs baǵıtın hám tezligin ózgerte almaydı.

6. QOZǴALIS MUǴDARINIŃ SAQLANIW NIZAMI

Materiallíq tochkalar yaki deneler toplamına mexanikalíq sistema delinedi. Sistemadaǵı denelerdiń ózara tásirleri sistemanıń ishki kúshlerin quraydı. Eger mexanikalíq sistemaǵa sırtqı kúshler tásir etpese sistema jabıq yaki izolyatsiyalanǵan boladı. Eger bir neshe denelerden quralǵan mexanikalíq sistema bar bolsa, sistemadaǵı denelerdiń ózara tásir kúshleri, Nyutonnıń ushınchi nızamına muwapıq, muǵdar jaǵınan teń, baǵıtları bir-birine qarama-qarsı boladı, yaǵnıy ishki kúshlerdiń geometriyalíq jıyındısı nolge teń boladı.

İzertlenip atırǵan mexanikalíq sistema n deneden ibarat bolsın. Sistemadaǵı dene massaları m1, m2,..., mn tezlikleri 1, 2, ..., n ishki kúshlerdiń teń tásir etiwshisi F', sırtqı kúshlerdiń teń tásir etiwshisi F bolsın. Hár bir dene ushın Nyutonnıń ekinshi nızamın qollanamız.

d
	m1 1 F1		F1
dt

d
	m2 2	F2		F2
dt

.......... .......... .........
d
	mn n	Fn		Fn
dt

Bul teńlemelerdi aǵzama-aǵza qosıp tómendegini payda etemiz:

(m1 1+ m2 2+...+ mn n)=

... F

Mexanikalíq sistemanıń ishki kúshleriniń geometriyalíq jıyındısı nolge teń bolǵanlıǵı ushın

(m1 1+ m2 2+...+ mn n)= Fá + Fǵ + ... + Fn

yaki

dр

...

(3.18)

Solay etip, mexanikalíq sistema impulsınan waqıt boyínsha alınǵan tuwındı, sistemaǵa tásir etiwshi sırtqı kúshlerdiń geometriyalíq jıyındısına teń eken.

Mexanikalíq sistema tuyıq bolǵanı ushın

F1+ F2 + ... + Fn = 0

Solay etip,

(m1 1+ m2 2+...+ mn n)= 0

yaki

(mi i )

i 0

yaǵnıy

mi i

const

(3.19)

n 1

teńlik qozǵalıs muǵdarınıń (impulstıń) saqlanıw nızamın ańlatadı: Oǵan muwapıq tuyıq mexanikalíq sistemanıń impulsı waqıt ótiwi menen ózgermeydi. Bul juwmaq klassikalíq mexanika ushın ǵana orınlı bolıp qalmay, bálki tábiyattıń fundamental nızamlarınan biri esaplanadı.

Bekkemlew ushın sorawlar:

1.Nyutonnıń birinshi nızamı qanday hallarda orınlanadı?

2.Massa, kúsh túsiniklerin táriypleń .

3.Nyutonnıń ekinshi nızamı ulıwma kórinis ańlatpasın jazıń hám túsindiriń.

4.Nyutonnıń úshinshi nızamın táriypleń.

5.Massa orayí haqqındaǵı teoremanı túsindiriń.

6.İmpulstıń saqlanıw nızamın túsindirip beriń.

5-tema. Mexanikalíq jumıs hám quwatlılíq

Jobası:

1.Energiyasistemanıń halat funktsiyası sıpatında. İlgerlemeli hám aylanbalı qozǵalısta jumıs hám kinetikalíq energiya. Quwat.

2.Potentsial energiya. Potentsial energiya menen kúsh arasındaǵı baylanıs.

3.Energiyanıń saqlanıw nızamı.

Tayanısh sóz hám túsinikler: Jumıs, mexanikalíq jumıs, oń hám teris jumıs, quwat, energiya, kinetikalíq energiya, sistemanıń halat funktsiyası, joqarıǵa kóterilgen deneniń potentsial energiyası, deformatsialanǵan deneniń potentsial energiyası, konservativ, konservativ emes hám dissipativ kúshler, keńislik hám waqıttıń simmetriyalıǵı.

1. ENERGIYA SISTEMANIŃ HALAT FUNKTSIYASI SIPATINDA. İLGERLEMELI

HÁM AYLANBALI QOZǴALISTA JUMIS HÁM KINETIKALÍQ ENERGIYA.

QUWAT

İmpulstı deneniń mexanikalíq qozǵalısınıń belgili ólshemi sıpatında qaraw mumkin. Biraq deneniń bunday dinamikalíq xarakteristikasi barlíq qozǵalıs formaları ushın universal ólshem bola almaydı. Bunı tómendegi mısallarda kórip shıǵamız.

Tuwrı sızıqlı teń ólshewli qozǵalısta bolıp atırǵan deneni baqlayı3. Deneler ortasında súykelis bar bolǵanlıǵı ushın deneler qızadı, yaǵnıy bunda denelerdiń mexanikalíq qozǵalısı usı denelerdi qurawshı molekulalardıń xaotikalíq – jıllılíq qozǵalısına aylanadı. Biraq deneniń impulsı tuwrı sızıqlı teń ólshewli qozǵalısta ózgermey qaladı, biraq ol ajralıp shıqqan jıllılíq muǵdarın xarakterlemeydi. Solay etip, qozǵalıs joǵalmaydı, bálki materiya qozǵalısınıń basqa formalarına ótedi.

Demek, qozǵalıs formalarınıń ulıwma ólshemi sıpatında jańa fizikalíq shama bolıwı kerek. Bunday fizikalíq shama energiya. Energiya hár qanday kórinistegi materiya qozǵalısınıń universal muǵdar ólshemi. Deneler sistemasınıń mexanikalíq qozǵalısı halatın anıqlaw ushın olardıń óz-ara jaylasıwın hám tezligin biliw jeterli boladı, gaz halatın xarakterlew ushın onıń kólemi, temperaturası hám basımın biliw zárúr. Energiya-sistema halatınıń funktsiyası bolıp tabıladı.

Deneler ortasındaǵı mexanikalíq qozǵalıstıń almasıwı yaki mexanikalíq qozǵalıstıń basqa qozǵalıs formalarına ótiwi denelerdiń ózara tásiri nátiyjesinde ámelge asırıladı. Tájriybeler sol nárseni kórsetedi, bunday protsesslerde ótip atırǵan qozǵalıstıń shaması, kúsh penen orın awıstırıw shamasınıń kóbeymesine teń eken. Bul payda bolǵan fizikalíq shama jumıs delinedi. Demek, jumıs bir denedan basqa denege qozǵalıstı beriw ólshemi yaki energiyanıń bir deneden

		basqa denege ótiw ólshemi bolıp tabıladı.
	F	basqa denege ótiw ólshemi bolıp tabıladı.
F	F
n		Eger materiallíq tochka turaqlı kúsh F (1-súwret) tásirinde s
F F F
n
		aralíqga kóshse, onda kúshtiń jumısı:
	F	aralíqga kóshse, onda kúshtiń jumısı:

		A = F S	(4.1)
	S	Bunda F - F kúshtiń orın awıstırıw baǵıtına proektsiyası
1-su'wret		Bunda F - F kúshtiń orın awıstırıw baǵıtına proektsiyası
1-su'wret		bolıp,
		bolıp,
		F = F cos	(4.2)
1 súwrette - deneniń qozǵalıs baǵıtı menen F kúsh arasındaǵı múyes8. (2)-ni esapqa
alıp, (1)-ni tómendegishe jazamız:
		A = F S cos	(4.3)

1)Eger kúsh baǵıtı menen orın awıstırıw baǵıtı arasındaǵı múyesh <90o bolsa, onda cos >0. Demek, kúsh oń jumıs orınlaydı (A> 0).

2)Eger > 90o bolsa, onda cos < 0. Bunda kúsh teris jumıs orınlaydı (A < 0). Máselen, súykelis kúshi hám tormozlaw kúshi;

3) Eger kúsh baǵıtı orın awıstırıwǵa tik baǵıtlanǵan bolsa, = 90o, onda cos =0, demek, kúshtiń orınlaǵan jumısı nolge teń, yaǵnıy energiya ózgermeydi. Eger málim bir aralíqta kúsh shaması ózgermeli bolsa, onda orınlanǵan jumıstı esaplaw ushın aralíqtı elementar orın awıstırıwlarǵa bólıp shıǵamız, bul elementar orın awıstırıwlarda, kúshti turaqlı shama dep esaplasa boladı (2-súwret). Hár bir elementar orın awıstırıwda orınlanǵan elementar jumıstı esaplap, keyin bul elementar jumıslardıń algebraik jıyındısın alsaq, onda ózgeriwshi F kúshtiń S aralíqta orınlaǵan jumısı tómendegishe ańlatıladı:

n	n
А Ai	Fi Si cosi	(4.4)
i 1	i 1

S nolge umtılǵanda (ń) den limit alsaq,

	n
A lim ( Fi		Si ) F dS	(4.5)
S 0	i 1	S
	i 1	S

(5) integraldı esaplaw ushın F kúshtiń S aralíqqa baylanıslılıǵın biliw zárúr.

Praktikada, tek kúshtiń orınlaǵan jumısın biliw ǵana emes, bálki qanday waqıt aralıǵında usı jumıs orınlanıwı da úlken áhmiyetke iye. Sonıń ushın kúshtiń qanday tezlik penen orınlaǵan jumısın xarakterlew ushın quwat túsinigi kiritiledi. Waqıt birligi ishinde, F kúsh orınlaǵan jumısqa san jaǵınan teń bolǵan fizikalíq shama quwat (N) delinedi:

F
			N =		t		(4.6)
Eger	kúsh	ózgermeli	bolsa,			qurılmanıń	quwatın
anıqlaw ushın (6) dan limit alamız:
S				A
S		N lim		A		dA	(4.7)
2-сурет		N lim					(4.7)
2-súwret			t 0	t		dt

bunda N bir zamattaǵı quwat delinedi. (3) ti itibarǵa alsaq, (7) ańlatpa tómendegi kóriniske iye boladı:

N=F	ds	F v	(4.7’)

Demek, bir zamattaǵı quwat san jaǵınan tezlik turaqlı bolǵanda kúshtiń tangentsial qurawshısınıń tezlikke kóbeymesine teń boladı.

Jumıs hám quwat birligin belgileyik. Xalíqara birlikler sisteması (Sİ) da jumıs birligi qılıp, kúsh baǵıtında deneni bir metr aralíqqa bir Nyuton kúsh tásirinde kóshiriwde orınlanǵan jumıs qabıl etilgen. Bul jumıstıń birligi Djoul (J), 1J=1 Nm. Quwat birligi etip Vatt (Vt) qabıl etilgen. 1 Vatt bir sekund dawamında bir joul jumıs orınlaytuǵın qurılma yaki mexanizmniń quwatı, 1Vt = 1J/1s.

Denelerdiń qozǵalısı sebepli payda bolǵan energiya kinetikalíq energiya delinedi. Bazı bir

m massalı dene turaqlı F kúsh tásirinde óziniń qozǵalıs tezligin 1		den 2 mániske shekem
ózgertrsin. Ol waqıtta m massalı deneniń qozǵalıs teńlemesi tómendegishe ańlatıladı:
F m	d	(4.8)
	dt

(8) teńlemeniń eki tárepine dt=ds ge skalyar kóbeytemiz:

FdS m	d	dt m d	(4.9)
	dt

Málim bir S1 – S2 aralíqta deneniń orınlaǵan jumısın esapqa alıw ushın (9)-nıń shep hám oń táreplerin S1 hám S2 aralíqlar hám de 1 hám 2 tezlik intervalı arasında integrallaymız:

s2	s2	2
dA FdS m d			(4.10)
s1	s1	1

(10) teńliktiń chep tárepi F kúsh orınlaǵan tolíq jumısqa teń, m = const bolsa, oń tárepi tómendegi kóriniske iye boladı:

		A	m 2	m 2
			2			1				(4.11)
			2	2						(4.11)
			2	2
	m 2
(11) teńliktegi		E deneniń kinetikalíq energiyasınıń ańlatpası bolıp tabıladı. Bul
(11) teńliktegi	2
	2
halda (11) tómendegi kóriniste jazıladı:
		A E E				E		m 2	m 2
								2	1	(4.12)
					2		1	2	2	(4.12)
					2		1

Demek, deneniń kinetikalíq energiyasınıń ózgerisi denege tásir etiwshi kúshtiń orınlaǵan jumısına san jaǵınan te4. Eger 1 = 0 bolsa,

E	m 2
		(4.13)
	2

Solay etip, m massalı dene tezlik penen qozǵalǵanda, E kinetikalíq energiyaǵa iye boladı. (13) formula dara jaǵdayda, materiallíq tochkanıń kinetikalíq energiyası dep aytıladı. Hár qanday mexanikalíq sistemanı materiallíq tochkalar sisteması dep qarawımız mumkin bolǵanı ushın mexanikalíq sistemanıń kinetikalíq energiyası usı sistemanı quraǵan materiallíq tochkalardıń kinetikalíq energiyalarınıń jıyındısına teń, yaǵnıy:

	n	mi	2
E Ei		mi	i	(4.14)
E Ei		2		(4.14)
	i 1	2
	i 1

bunda mi hám i -materiallíq tochkanıń massası hám tezligi. Demek, hár qanday mexanikalíq sistemanıń kinetikalíq energiyası usı sistemaǵa kirgen materiallíq tochkalardıń massası hám qozǵalıs tezligi menen anıqlanar eken.

Bul áhmiyetli juwmaqtı qısqasha qılıp tómendegishe táriyplew mumkin: sistemanıń kinetikalíq energiyası - onıń qozǵalıs halatı funktsiyası bolıp tabıladı.

Bir waqıtta aylanbalı hám ilgerlemeli qozǵalısta bolǵan deneniń kinetikalíq energiyası onıń aylanbalı hám ilgerlemeli qozǵalısına sáykes keliwshi kinetikalíq energiyalar jıyındısına teń boladı.

Aylanbalı qozǵalısta bolǵan dene kinetikalíq energiyasın qarap shıǵayı3. Deneni absolyut qattı dene dep hám onı materiallíq tochka dep qaraw mumkin bolǵan n bólekke bóleyik. Eger i- bólektiń massası mi, sızıqlı tezligi i, qozǵalıs bolıp atırǵan sheńber radiusi ri, aylanbalı qozǵalıs múyesh tezligi bolsa, bul bólketiń kinetikalíq energiyası

	m	2
Ei	i	i			(4.15)
Ei	2				(4.15)
	2
boladı. i = ri ekenin esapqa alsaq:
	m		2 r 2
Ei	i			i	(4.16)
Ei		2			(4.16)
		2

Deneniń kinetikalíq energiyası onıń bólekleriniń kinetikalíq energiyaları jıyındısına teń:

	n	n	m r	2	2	n
	E Ei	2	i i			mi ri2 ,
	E Ei	2	2		2	mi ri2 ,
	i 1	i 1	2		2	i 1
n
bunda mi ri	2 I bolǵanlíqtan:

i 1

E	I	2	(4.17)

	2
	2

Bul formulanı ilgerlemeli qozǵalıs kinetikalíq energiyası (13) menen salıstırsaq, dene massası ornında deneniń aylanıs kósherine salıstırǵanda inertsiya momenti, sızıqlı tezlik ornına múyesh tezlik turǵanın kóremiz.

Denege kúsh tásir qılıp, onı qandayda bir kósher dógereginde aylanbalı qozǵalısqa keltirgenda onıń bólekleri jıljıydı. Demek, jumıs orınlanadı. Bul jumıs aylanıp atırǵan dene kinetikalíq energiyası ózgerisine teń boladı.

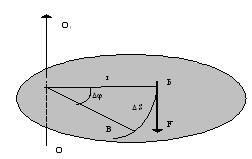
Dene OO1 qozgalmas kósher dógereginde aylanbalı qozǵalısta bolsın. Juwmaqlawshı F kúsh deneniń B tochkasına qoyılǵan bolıp, bul tochka aylanıs kósheridan r uzaqlíqta bolsın (3- súwret). Dene F kúsh tásirinde múyeshge burılǵanda, B tochka V tochkaǵa jıljıp S doǵanı sızadı. Onda orınlanǵan elementar jumıs:

	A = F S					(4.18)
buladi, S = r bolǵanı ushın A = Fr boladı. Fr = M kúsh momenti bolǵanlíqtan:
	A = M
Tolíq jumıs bolsa bul ańlatpanı integrallaw arqalı anıqlanadı:

	A Md					(4.19)
	0
	Eger deneniń			aylanbalı	qozǵalısı	dawamında
	kúsh momenti turaqlı (M = const) bolsa, (19) dan
	ulıwma orınlanǵan jumıs
			A M			(4.20)
	boladı. Demek, aylanbalı qozǵalısta orınlanǵan
	jumıs kúsh momenti			menen	burılıw	múyeshshiń
	kóbeymesi arqalı anıqlanar eken.
3-súwret
Sheńber boylap ózgermeli qozǵalıs ushın (20) ańlatpa tómendegishe jazıladı:
	dA Md I	d	dt I d
	dA Md I		dt I d
		dt
Burılıw múyeshi 1	den 2 geshe ózgergende múyeshlik tezlik 1 den					2 shekem

ózgergen bolsa, ulıwma jumıstı esaplaw ushın usı shegaralarda joqarıdaǵı ańlatpanı integrallaymız:

			2		2
dA dA Md I d							(4.21)
			1		1
yaki
A M (		)		I 2		I 2
				2		1	(4.22)
	2						(4.22)
	2		1	2		2
				2		2

(22) dan kórinip tur, aylanbalı qozǵalısta deneniń kinetikalíq energiyasınıń ózgerisi qoyılǵan juwmaqlawshı kúsh momentine baylanıslı.

Dene bir waqıtta aylanbalı hám ilgerlemeli qozǵalısta bolsa, bunday qozǵalıs ushın tolíq kinetikalíq energiya:

			m 2	I 2
E E	E		с		(4.23)
		айл
илг			2	2

bunda m - deneniń massası, I - deneniń massa orayínan ótken kósherge salıstırǵanda inertsiya momenti, - usı kósherge salıstırǵanda aylanbalı qozǵalıstıń múyesh tezligi, s - massa orayínıń sızıqlı tezligi.

2. POTENTSIAL ENERGIYA. POTENTSIAL ENERGIYA MENEN KÚSH

ARASINDAǴI BAYLANIS

Denelerdiń yaki dene bólekleriniń bir-birine salıstırǵanda jaylasıwına baylanıslı bolǵan energiya potentsial energiya dep ataladı.

Sistemanıń potentsial energiyasın anıqlaw ushın sistemadaǵı denelerdiń ózara jaylasıwın hám olar arasındaǵı tásir kúshlerdi biliwimiz kerek.

Mısal sıpatında, denege tásir etiwshi awırlíq kúshi saldarınan deneniń potentsial energiyasınıń ózgerisini kórip shıǵayı3. Deneniń Jer betinen kóteriliw biyikligi h, Jerdiń radiusına salıstırǵanda bir qansha kishi bolsa, R = mg = const dep esaplaw mumkin, m - deneniń massası.

Eger dene uzınlíqtaǵı qıya	tegislik boyínsha súykelissiz túsip	atırǵan bolsa
(4(a)súwret), awırlíq kúshi orınlaǵan jumıs tómendegi shamaǵa teń boladı:
A = R cos = mg (h1 h2) = U1 U2		(4.24)
bunda	h = h1 h2 = cos	(4.25)


h1
	h2

qıya tegisliktiń biyikligi, -qıya tekisliktiń gorizontǵa salıstırǵanda qıyalíq múyeshi, U=mgh deneniń potentsial energiyası, (24) den kórinip tur, sistema potentsial energiyasınıń ózgerisi san jaǵınan, sırtqı kúshler sistemanıń tezligin ózgertpesten bir halattan ekinshi halatǵa ótkeriwde orınlaǵan jumısına teń bolar eken.

4(a)(a) sú- wretсурет

Endi dene qozǵalıs traektoriyasi ıqtıyarıy iymek sızıqtan ibarat bolsın (4(b)-súwret). Onda bul iymek sızıqtı n kishi tuwrı sızıqlı bóleklerge bólemız. Mine usı hár bir elementar bólekte awırlíq kúshiniń elementar orınlaǵan jumısı

Ai = r i cosI = r hi (4.26) boladı. Bunda hi - vertikal tuwrı sızıq i – bólektiń proektsiyası. Elementar bóleklerde

orınlanǵan jumıslardıń jıyındısı, iymek sızıqlı jolda awırlíq kúshi orınlaǵan jumıstı ańlatadı:

n	n
A Ai	P hi Ph mgh	(4.27)
i 1	i 1

h1 i

4 (б)-сурет

4(b)súwret

Solay etip, awırlíq kúshiniń jumısı joldıń dáslepki hám aqırǵı tochkalarınıń koordinatalarına baylanıslı eken.

Makroskopik mexanikada ushraytuǵın kúshler eki potentsial (konservativ) hám dissipativ (kontservativ emes) kúshlerge ajratıladı.

Eger tuyıq jol (kontur) boyínsha kúshtiń orınlaǵan jumısı nolge teń bolsa, bul kúshler potentsial (yaki konservativ) kúshler dep ataladı.

Eger sistema bazı bir kúsh tásirinde áa ǵ jol boyınsha (5 -súwret) bir orınnan ekinshi orınǵa kóshsin.

	а		Bunda A1a2 ǵa teń jumıs orınlanadı. Eger sistema ekinshi orınǵa ábǵ jol
1		2	boyínsha ótse, onda orınlanǵan jumıs A1b2 ǵa teń boladı. Konservativ

kúshlerdiń anıqlamasına muwapıq A1a2 = A1b2.

5 – сурет

5-súwret

Kúshler sistemanıń konfiguratsiyasina (koordinatlarına) baylanıslı bolmaǵanlıǵı ushın A1b2 = A2b1 boladı. Sonıń ushın, A1a2 + A2b1 = 0.

Demek, usı kúsh tásirinde sistema yaki deneni bir halattan ekinshi bir halatǵa kóshiriwde orınlanǵan jumıs A1a2 = A1b2 = A22 orın awıstırıw trektoriyasınıń formasına baylanıslı bolmaydı,

bul kúsh konservativ (yaki oraylíq) kúsh dep ataladı.

Konservativ kúshlerge awırlíq kúshleri, elastik kúshleri hám zaryadlanǵan bólekshelerdiń ózara elektrostatik tásir kúshleri mısal bola aladı.

Konservativ bolmaǵan barlíq kúshler dissipativ kúshler dep ataladı.

Dissipativ kúshlerge, súykelis kúshleri hám suyıqlíqta yaki gazde háreketlenip atırǵan denege tásir etiwshi qarsılíq kúshleri kiredi.

Elastik kúsh penen potentsial energiya arasındaǵı baylanıs. Elastik kúsh tásirinde, dene deformatsiyasınıń kishi (dx shamaǵa) ózgerislerinde, orınlanǵan elementar jumıs tómendegige teń boladı.

dA = Fdx = kxdx	(4.28)
Jumıstıń tolíq mánisin anıqlaw ushın (28) formulanı deformatsiyalanbaǵan halattan (xo=
0) deformatsiya shaması x mánisleri shegarasında integrallaymız:

		x							kx2			kx	2
		A kxdx										0		(4.29)
		A kxdx								2		2		(4.29)
		x0								2		2
		x0
Bul shamaǵa tiykarlanıp prujinanıń potentsial energiyası ózgeredi:
		U			kx2		U				,			(4.30)
		U	n		2		U			0	,			(4.30)
			n							0

bunda U 0	kx2	deformatsiyalanbaǵan deneniń potentsial energiyası, onı nolge teń
	0
	2
	2
dep alsaq, (30) tómendegishe jazıladı:
			U			kx2		.						(4.31)
			U	П				.						(4.31)
				П	2
					2

Solay etip, (29) dan kórinip tur, elastik dene deformatsiyalansa, onda jumıs deformatsiyalanǵan dene energiyasınıń ózgerisine sarıplanadı. (4.31) ańlatpaǵa deformatsiyalanǵan deneniń potentsial energiyası delinedi.

Potentsial maydannıń hár bir tochkasına bir tárepten denege tásir etiwshi f kúsh vektorınıń bazı bir mánisi sáykes kelse, ekinshi tárepten, dene U potentsial energiyasınıń mániside sáykes

keledi.
Demek, kúsh penen potentsial energiya arasında málim baylanıs bar bolıwı			kerek. Bizge
belgili, jumıs potentsial energiya esabınan orınlanadı, yaǵnıy:
	A = U		(4.32)
U – sistema potentsial energiyasınıń kemeyiwin kórsetedi.
(4.28) menen (4.29) ni salıstırıp tómendegini tabamız:
Fs S = U ,
bunnan
F s	U	.	(4.33)

	S

(4.33) ańlatpada Fs – bul F kúshtiń s orın awıstırıw boyínsha proektsiyasi. Fs tıń berilgen tochkadaǵı mánisin tabıw ushın limitge ótiw kerek:

F lim		U	(4.34)

s	s 0	S

U, s kósher boylap kóshirilgende ǵana emes, hátte basqa baǵıtlar boylap kóshirilgende de

ózgergenligi ushın (4.34) formuladaǵı limit U dan s boyínsha tuwındıdan ibarat boladı, yaǵnıy:

(4.35)

(35) qatnas keńisliktegi ıqtıyarıy baǵıt ushın,

x, y, z

dekart koordinata kósherleri

boyínsha baǵıtlar ushında orınlı yaǵnıy:

(

k )

(4.36)

Demek, kúsh potentsial energiyanıń qarama-qarsı belgi menen alınǵan gradientine teń eken

F = gradU.

(4.37)

3. ENERGIYANIŃ SAQLANIW NIZAMI

Energiyanıń saqlanıw nızamı tájriybelerden alınǵan nátiyjelerdi ulıwmalastırıw joli menen shıǵarılǵan.

Aytayıq, tuyıq sistema ishindegi materiallíq tochka massaları m1, m2, ..., mn tezlikleri1, 2, ..., n bolsın. Denelerge tásir etiwshi konservativ kúshler F1, F2, ..., F'n hám teń tásir etiwshi sırtqı kúshler F1, F2, ..., Fn bolsın. <<s bolǵan halda materiallíq tochka massaları turaqlı boladı. Nyutonnıń ekinshi nızamına muwapıq

<<< < Предыдущая 1 23 / 193 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 > Следующая >>>

Соседние файлы в предмете Физика

#
09.08.20246.47 Mб23Fizika pani boyinsha lekciyalar.pdf
#
26.10.20241.35 Mб4Házirgi zaman tabiyiy pánler konсepсiyası.pdf
#
26.10.2024785.13 Кб0Kosmoslıq nurlar fizikası.pdf
#
26.10.20242.52 Mб4Mexanika páni boyınsha lekciya tekstleri-1.pdf
#
11.08.202411.44 Mб1Mexanika páni boyınsha lekciya tekstleri.pdf
#
11.08.20246.69 Mб0Mexanikadan maseleler toplami_new.pdf