
Fizika pani boyinsha lekciyalar
.pdf
|
|
|
S |
|
|
|
|
|
|
|
|
|
(1.2) |
|
|
t |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
Materiallíq |
tochkanıń tezligi vektor |
|
shama bolıp, Sİ |
birlikler sistemasıda |
m/s |
||||||||
(metr/sekund) da ólshenedi. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Qozǵalıstıń bir zamattaǵı tezligin xarakterlew ushın waqıttı sonday kishireytip baramız, |
|||||||||||||
nátiyjede ortasha tezlik bir zamattaǵı tezlikke jaqınlasıp baradı, yaǵnıy |
|
|
|
|
|||||||||
|
|
|
|
|
S |
dS |
|
|
|
dS |
|
||
|
|
lim |
|
|
|
; |
|
|
|
|
(1.3) |
||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
dt |
|
|
|
dt |
|
|
|
|
|
t o |
t |
|
|
|
|
|||||
(1.3)-teńlikten kórinip tur, tezliktiń san mánisi joldan waqıt boyínsha alınǵan birinshi |
|||||||||||||
tartipli tuwındı menen ańlatılar eken. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Dene qozǵalısınıń tezligi teń waqıt aralíqlarında birdey (v) muǵdarǵa ózgerip baratuǵın |
|||||||||||||
qozǵalısqa teń |
ózgermeli qozǵalıs |
delinedi. |
|
Bunday qozǵalıs |
teń |
|
tezleniwshi hám |
teń |
|||||
ásteleniwshi qozǵalıslarǵa bólinedi. Eger materiallíq tochka tezligi t - to waqıt dawamında |
V - |
||||||||||||
|
|
o |
|
|
|
|
|
|
|
|
|||
Vo ge ózgerse, dene alǵan tezleniw: |
a t to |
|
menen ańlatıladı. t0 |
= 0 hám Vo = 0 ushın |
|||||||||
materiallíq tochka tezleniwi
a t
ge teń boladı hám m/s2 da ólshenedi. Materiallíq tochkanıń ıqtıyarıy waqıttaǵı tezligi
0 a t
basıp ótilgen jol uzınlıǵı
S 0 t at 2
2 formula menen anıqlanadı. Eger 6 teńlikte 0 0 bolsa,
S a t 2
2
boladı. Jol menen tezlik arasındaǵı baylanıs:
2 2
S o
2 a
yaki
2 o2 2 a S
formulalar menen ańlatıladı.
(1.4)
(1.5)
(1.6)
(1.7)
(1.8)
(1.9)
3. TEŃ ÓLSHEWLI HÁM TEŃ ÓLSHEWSIZ AYLANBALI QOZǴALIS.
İymek sızıqlı qozǵalısta dene tezliginiń san mánisi turaqlı bolsa, bunday iymek sızıqlı qozǵalıs teń ólshewli iymek sızıqlı qozǵalıs delinedi. Bunday qozǵalıstaǵı materiallíq tochkanıń normal hám tangentsial tezleniwlerin kóreyik (1-súwret).
12

|
|
|
|
A hám B tochkadaǵı tezlikler ayırması: V1 - Vo = at = FD. Teń tásir etiwshisi FD nı FC |
||||||||||||||
|
|
|
|
|
|
|
|
|
hám FE ge ajratamiz. |
|
|
|
|
|
|
|||
|
|
|
V0 F a |
E |
at = FD bolǵanlíqtan. a nı a |
hám an |
qurawshılarǵa |
|||||||||||
A |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
ajratamiz. AB=dS |
dep alsaq, |
B |
tochka |
A |
tochkaǵa |
||||
|
|
|
|
|
|
B |
|
|
||||||||||
|
|
|
|
an |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
jaqınlastırılǵanda |
E |
|
tochka AD |
ústine túsedi. |
Sonday |
|||||
|
|
|
|
V1 |
|
|
V1 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
D |
shártte OAB AED; OA = R; AB = S; |
|
|
|||||||||
|
|
R |
|
C |
|
|
|
|||||||||||
|
|
|
|
|
S |
|
DE |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.1) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
R |
B |
|
|
|
|
|
|
|
|
|
|
O |
1-suwret |
|
S t |
|
|
|
(2.2) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
an a sin |
|
|
|
(2.3) |
|||||
|
|
|
|
|
|
|
|
DE |
sin; |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
at |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
DE a t sin |
|
|
|
(2.4) |
|||||
|
|
(2.3)-teńlikti esapqa alıp |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
DE an t |
|
|
|
|
|
(2.5) |
|||
(2.2) hám (2.5) - teńliklerdi esapqa alıp, 1- teńliktit / R an t /
an 2 t / R t 2 / R
a |
n |
2 |
/ R |
(2.6) |
İymek sızıqlı qozǵalısta tangentsial tezleniw
|
|
a d / dt |
|
|
(2.7) |
||
|
|
menen ańlatıladı. |
|
|
|
||
|
|
6-teńlik |
iymek sızıqlı |
qozǵalısta |
normal |
tezleniwdi |
|
|
|
ańlatadı |
hám |
iymeklik radiusı boylap |
orayǵa |
baǵıtlanǵan |
|
|
|
|
|
|
|
|
|
R |
|
boladı. |
Tangentsial tezleniw |
iymek sızıqqa urınba halda |
|||
|
|
baǵıtlanǵan bolıp, tezliktiń ózgerisin ańlatadı. Deneniń tolíq |
|||||
S |
|
tezleniwi: |
|
|
|
|
|
|
|
|
a d / dt a an |
|
|
(2.8) |
|
yaǵnıy a hám an lardıń geometriyalíq jıyındısına teń boladı. Materiallíq tochka R radiuslı sheńber boylap qozǵalıp
atırǵan bolsa, onıń qozǵalısı múyeshlik tezlik hám múyeshlik tezleniw menen xarakterlenedi. Materiallíq tochka t waqıt ótkende múyeshge burıladı (2-súwret).
Burılıw múyeshiniń waqıt birligi ishindegi ózgerisi menen anıqlanatuǵın vektorlíq shama materiallíq tochkanıń sheńber boyínsha múyeshlik tezligi delinedi.
|
lim |
|
|
, |
|
|
t o t |
|
t |
|
|
yaǵnıy |
|
|
|
|
(2.9) |
t |
|
|
|||
|
|
|
|
|
|
rad/s.
Materiallíq tochkanıń sızıqlı tezligi
13
2 |
1 |
1 |
2 |
|
|
lim S |
lim |
R |
R lim |
R , |
(2.10) |
||
t |
|||||||
t o t |
|
t o |
t o t |
|
|
||
Eger const |
bolsa, qozǵalıs sheńber boylap teń |
||||||
ólshewli boladı. Tochka tolíq bir márte aylanǵanda = 2 hám t = T boladı. Ol halda / t = 2 /T boladı. Aqırǵı teńlikten
|
|
T |
2 |
|
|
(2.11) |
3-suwret |
4-suwret |
|
|
|
|
|
|
|
|
|
|
||
|
|
kelip shıǵadı |
|
|
|
|
Waqıt birligi ishindegi aylanıslar sanı, aylanıs jiyiligi delinedi. |
|
|||||
|
|
n |
1 |
|
|
(2.12) |
|
|
|
T |
|
|
|
yaki |
|
n |
1 |
|
|
(2.13) |
|
(2 / ) |
2 |
||||
Múyeshlik tezleniw vektor shama bolıp, múyeshlik tezlikten waqıt boyínsha alınǵan tuwındı menen ańlatıladı.
|
d |
(2.14) |
|
dt |
|||
|
|
- rad/s2 da ólshenedi.
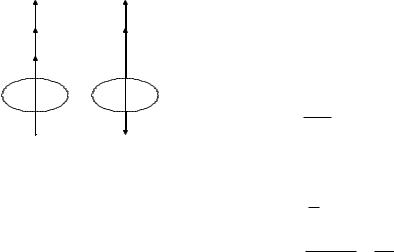
(2.14) – teńlikten múyeshlik tezleniw aylanıs kósheri boyínsha múyeshlik tezliktiń artıw baǵıtı boylap baǵıtlanǵanlıǵı kelip shıǵadı.
Eger qozǵalıs teń tezleniwshi bolsa, múyeshlik tezleniw vektorı múyeshlik tezlikke parallel (3-súwret), qozǵalıs ásteleniwshi bolsa, múyeshlik tezleniw ( ) múyeshlik tezlikke ( ) qaramaqarsı baǵıtlanǵan boladı (4-súwret).
4. Vertikal atılǵan dene qozǵalısı. Erkin túsiw
Jer betinde jaylasqan qálegen erkin dene Jer orayína qarap baǵıtlanǵan 9,81 m/s2 tezleniw menen túsiwi eksperimental túrde anıqlanǵan. Eń qızıqlısı sonda, bul tezleniw deneniń massasına, dúzilisine hám dáslepki tezligine baylanıslı emes. Bul tezleniwdi g háripi menen belgilew qabıl etilgen hám g=9,81 m/s2. Biz erkin túsiw tezleniwi g nı hámme waqıt oń shama dep esaplaymız. Sonıń ushın x kósheri joqarıǵa baǵıtlanǵan bolsa, ol halda tezleniw a = - g boladı.
Deneniń vertikal tegisliktegi qozǵalısın kórip shıǵayı3. Gorizontal baǵıttaǵı koordinatanı x penen, vertikal baǵıttaǵı koordinatanı u menen belgileymiz. Bizge belgili, eger gorizontqa salıstırǵanda múyesh astında shar atılsa, ol parabola boylap qozǵaladı. Bul shardıń kóshiwi tómendegishe sıpatlanadı:
y ( |
0 |
) |
y |
t gt 2 |
/ 2 |
(2.15) |
|
|
|
|
|
|
|
||
Shardıń gorizontal baǵıttaǵı kóshiwi |
|
|
|
|
|
|
|
x (0 ) x |
t |
|
(2.16) |
||||
kóriniste ańlatılsa, vertikal boylap kóshiwi bolsa (1) teńleme menen sıpatlanadı.
(2.16) teńlemeni t ǵa qarata sheship hám onı (2.15) teńlemege qoyıp tómendegige iye bolamız:
14

|
|
|
|
|
x |
|
|
|
1 |
|
|
x |
|
2 |
|
(v |
0 |
) |
y |
||
y (v |
|
) |
|
|
|
|
|
g |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
0 |
|
y |
(v |
0 |
) |
|
|
|
2 |
|
(v |
0 |
) |
|
|
|
(v |
0 |
) |
x |
|
|
|
|
|
|
x |
|
|
|
|
|
x |
|
|
|
||||||
x |
g |
|
|
x 2 , |
(2.17) |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
2(v |
0 |
) |
2 |
|
|
|
|
|
x |
|
|
|
Bul teńleme parabola teńlemesi bolıp tabıladı. Teńleme járdeminde dáslepki tezlikti anıqlaw múmkin, sonday-aq, shardıń tezligin onıń vertikal (v0)x hám gorizontal qurawshıları (v0)y járdeminde de tabıw múmkin. Aytaylíq, ∆t waqıt dawamında shar gorizontal baǵıtta ∆x, vertikal baǵıtta bolsa ∆u aralíqtı ushıp ótse, ol halda Pifagor teoremasına muwapıq shardıń tolíq sızıqlı kóshiwi tómendegige teń boladı:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
( x)2 |
( y)2 , |
(2.18) |
|||||||||
(2.18) teńlemeniń hár eki tárepine ∆t ǵa bólsek, |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
S |
|
|
|
x 2 |
|
y 2 |
(2.19) |
|||||||
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
t |
|
t |
|
||||||||
yaki |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.20) |
|
|
|
|
|
|
|
|
|
v |
2 |
|
2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
v0 x v0 y |
|
|||||||||||
boladı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Bunda v |
x |
v |
0 cos , |
v |
y |
v |
0 sin :sh ólshemli keńislikte bolsa |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
v |
2 |
2 |
2 |
|
(2.21) |
||||||||
|
|
|
|
|
|
|
|
|
v0 x v0 y v0z |
|
|||||||||||
kórinisinde boladı.
Fizikada kópshilik jaǵdaylarda vektor shamalar menen jumıs islewge tuwra keledi. Ol yaki bul fizikalíq shamanıń vektor shama ekenligi tajriybede anıqlanadı. Deneniń kóshiwi, tezlik, tezleniw, kúsh, impuls momenti, kuch impulsi, elektr maydan kernewliligi, 8.t.b. vektor shamalar bolıp tabıladı.
Tezliklerdi vektor usılda qosıwdı aǵıp atırǵan suwda qozǵalıp atırǵan qayıq mısalında kórsetiw múmkin. Qayıqtıń ∆t waqıt ichindegi suwǵa salıstırǵanda kóshiwin ∆S penen, suwdıń qurǵaqlíqqa salıstırǵanda kóshiwin ∆Sc menen belgileymiz. Ol jaǵdayda qayıqtıń qurǵaqlíqqa
salıstırǵanda kóshiwi ∆S’ tómendegishe boladı: |
|
|
|
|
|||
|
∆S’ = Sc + ∆S |
(2.22) |
|||||
Bul ańlatpanıń hár eki tárepin ∆t ǵa bólip jibersek, |
|
|
|||||
S |
, |
|
S |
c |
S |
(2.23) |
|
|
|
|
|
||||
|
|
|
|
|
|
||
t |
|
t |
t |
||||
|
|
||||||
kórinistegi teńlemege iye bolamız. |
|
|
|
|
|
|
|
Eger ∆t 0 bolsa, ol halda |
|
|
|
|
|
|
|
v, |
v |
c |
v |
(2.24) |
|||
|
|
|
|
|
|
||
boladı.
Bunda vc – suwdıń qurǵaqlíqqa salıstırǵanda tezligi, v – qayıqtıń suwǵa salıstırǵanda tezligi, v' - qayıqtıń qurǵaqta turgan qozǵalmas baqlawshıǵa salıstırǵanda tezligi. (2.24) ańlatpa tezliklerdi qosıw qádesi dep ataladı.
15
Gorizontga múyesh astında atılǵan dene qozǵalısı
Bazı bir dene gorizont penen múyesh qurawshı hám v0 ǵa teń bolǵan dáslepki tezlik penen atılǵan, dep kóz aldımızǵa keltireyik. Usı dene qozǵalıs traektoriyasınıń kórinisin, onıń qozǵalıs waqtın, kóteriliw biyikligin hám ushıw uzaqlıǵın anıqlayı3.
Deneniń qozǵalısın Jerge salıstırǵanda qarap, Jerdi sanaq bası etip alamız hám oǵan tuwrı múyeshli koordinatalar sistemasın jaylastıramız.
Dene tezliginiń ox hám oy kósherlerine proektsiyaları ushın tómendegi ańlatpalardı jazamız:
v |
x |
v |
cos |
|
|
|
0 |
|
|
(2.25) |
|
v |
|
v |
|
|
|
|
sin gt |
|
|||
|
y |
0 |
|
|
|
Deneniń koordinataları waqıt ótiwi menen ózgeredi. Sonıń ushın olar waqıttıń funktsiyaları sıpatında tómendegi kóriniste jazıladı:
x v0 cos t |
|
|
|
|
|
|
|
|
|
|
gt |
2 |
(2.26) |
|
y v0 sin t |
|
|
|
|
|
|
|
||
2 |
|
|||
Deneniń qozǵalısı gorizontal baǵıtta vx tezlikli teń ólshewli qozǵalıs penen hám vy dáslepki tezlikte joqarıǵa vertikal baǵıtlanǵan teń ásteleniwshi qozǵalıs jıyındısınan ibarat bolǵan quramalı qozǵalıs bolıp tabıladı. x hám u tıń (12) teńlemedegi ańlatpalarınan t waqıttı joq etip, traektoriya teńlemesin tabamız:
y tg x |
|
|
g |
|
x 2 |
(2.27) |
|
|
|
|
|||
|
2 |
cos2 |
|
|||
|
2v |
|
|
|||
|
|
0 |
|
|
|
|
(2.27) teńlemedegi x hám x2 aldındaǵı koeffitsientler turaqlı shamalar, olardı |
a hám b |
|||||
menen belgilesek, onda |
|
|
|
|
|
|
y ax bx2 |
|
|
(2.28) |
|||
teńleme payda boladı, bul parabola teńlemesi. Demek, gorizontqa salıstırǵanda múyesh astında atılǵan dene parabola boyínsha qozǵalar eken.
Traektoriyanıń eń joqarǵı tochkasında tezliktiń vertikal qurawshısı nolge teń, yaǵnıy vy=0. Sonıń ushın deneniń maksimal biyiklikke kóteriliw waqtı t1 di
v0 sin gt1 0
teńlikten anıqlaw múmkin, bunnan |
|
|
|
t |
|
v0 sin |
(2.29) |
|
|||
1 |
|
g |
|
boladı.
Deneniń kóteriliw biyikligi tek ǵana tezliktiń vertikal qurawshısına baylanıslı. Maksimal kóteriliw biyikligi hm (12) formuladaǵı u tıń ańlatpasına maksimal biyiklikke kóteriliw waqtı t1 diń mánisin qoyıp anıqlanadı, yaǵnıy:
|
gt 2 |
|
v |
0 |
sin |
|
g |
v |
0 |
sin 2 |
|
v |
2 sin2 |
|
(2.30) |
||
hm v y t1 |
1 |
v0 sin |
|
|
|
|
|
|
|
|
|
0 |
|
||||
2 |
|
|
g |
2 |
|
|
g |
|
|
2g |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16
Awırlíq kúshi tásiri astında qozǵalıp atırǵan deneniń kóteriliw waqtı onıń túsiw waqtına te4. Sonıń ushın deneniń tolíq ushıw waqtı
t 2t1 |
2v0 sin |
|
g |
(2.31) |
|
|
|
|
qatnasınan tabıladı.
Deneniń ushıw uzaqlıǵı tek tezliktiń gorizontal qurawshısına baylanıslı. Sonıń ushın t ushıw waqtınıń mánisin (12) ańlatpaǵa qoyıp, deneniń ushıw uzaqlıǵın l tabıw múmkin:
|
2v |
0 |
sin |
|
v |
2 |
|
|
|
|
|
|
|
0 |
|
(2.32) |
|
l v x t v0 cos |
|
g |
|
g sin 2 |
||||
|
|
|||||||
Keyingi formuladan kórinip tur, dáslepki tezliktiń málim mánisinde hám 2 900 yaki
450 bolǵanda dene eń uzaq aralíqqa barıp túsedi. Múyeshti durıs tańlay biliw hám nıshanǵa shekem bolǵan aralíqtı, hámde snaryadtıń dáslepki tezligin biliw, zeńbirekti nıshanǵa tuwrı gózlew mashqalasın sheshiwge imkaniyat beredi.
Bekkemlew ushın sorawlar:
1.Mexanikalíq qozǵalıs dep qanday qozǵalısga aytıladı?
2.Waqıt hám keńislik túsinigi neden ibarat?
3.Tuwrı sızıqlı teń ólshewli qozǵalısta tezlik, tezleniw dep nege aytıladı?
4.İymek sızıqlı qozǵalısta materiallíq tochkanıń normal hám tangentsial tezleniwleri qanday baǵıtǵa iye?
5.Materiallíq tochkanıń sheńber boyínsha qozǵalısında sızıqlı tezlik hám múyeshlik tezleniw dep nege aytıladı?
2.Erkin túsiw dep nege aytıladı?
3.Erkin túsiw tezleniwinin shaması nelerge baylanıslı?
4.Tezliklerdi qosıw qádesin túsindiriń?
5.Awırlíq kúshi tásiri astında qozǵalıp atırǵan deneniń kóteriliw waqtı hám maksimal biyikligi qanday fizikalíq shamalarga baylanıslı?
6.Dáslepki tezliktiń koordinata kósherlerindegi proektsiyaların tabı4.
7.Gorizontǵa salıstırǵanda múyesh astında atılǵan deneniń qozǵalıs traektoriyası qanday boladı?
8.α nıń qanday mánisinde deneniń ushıw uzaqlıǵı maksimal boladı?
3-tema. Dinamika
Jobası:
1.Dinamikanıń tiykarǵı wazıypası. Klassikalíq mexanikada halat túsinigi.
2.Nyutonnıń birinshi nızamı.
3.Nyutonnıń ekinshi nızamı.
4.Nyutonnıń úshinshi nızamı.
5.Massa orayí. Massa orayínıń qozǵalısı haqqındaǵı teorema.
6.Qozǵalıs muǵdarınıń saqlanıw nızamı.
17

Tayanısh sóz hám túsinikler: Massa hám onıń birligi, kúsh hám onıń birligi, awırlíq kúshi, erkin dene, inertlilik, inertsiya, inertsial sanaq sisteması, Nyutonnıń birinshi nızamı, dinamikanıń tiykarǵı nızamı, impuls, tásir, keri tásir, Nyutonnıń úshinchi nızamı, massa orayí, awırlíq orayí.
1. DINAMIKANIŃ TIYKARǴI WAZIYPASI. KLASSIKALÍQ MEXANIKADA HALAT
TÚSINIGI
Mexanikanıń kinematika bóliminde qozǵalıs nızamların úyreniw, bul qozǵalıslardı júzege keltirgen sebepler menen baylanıslı bolmaǵan halda alıp barıladı. Mexanikanıń dinamika bóliminde bolsa denelerdiń qozǵalısı usı qozǵalıstı júzege keltiriwshi sebepler menen baylanıslı halda úyreniledi. Dinamikanıń wazıypası tiykarınan tómendegilerden ibarat:
1)dene qozǵalısı málim bolsa, oǵan tásir etiwshi kúshti anıqlaw;
2)denege tásir etiwshi kúsh málim bolǵan jaǵdayda qozǵalıs nızamın anıqlaw.
Tájriybe sol nárseni kórsetedi, kúsh tásirinde denelerdiń tezligi ózgeredi, yaǵnıy olar tezleniw aladı. Qozǵalıs protsessinde materiallíq tochkanıń (yaki materiallíq tochkalar sisteması) koordinataları, yaǵnıy radius–vektorı ózgeredi.
Tájriybe sonı kórsetedi, materiallíq tochkanıń berilgen waqıttaǵı halatı radius-vektorı r hám tezligi V menen, yaǵnıy onıń x,y,z koordinataları hámde koordinata kósherleri boyínsha tezliktiń proektsiyaları Vx, Vy, Vz, menen anıqlanadı. N materiallíq tochkadan ibarat sistemanıń berilgen waqıttaǵı halatı sistemadaǵı materiallíq tochkalardıń radius - vektorları r1, r2, … rN hám olardıń tezlikleri V1, V2, …. VN, menen ańlatıladı. Demek, hár bir materiallíq tochkanıń halatı bir-birine baylanıslı bolmaǵan eki shama, r hám V menen anıqlanadı.
Dene inertliliginiń ólshemi massa dep ataladı. Demek, deneniń massası qansha úlken bolsa, onıń inertligi hám sonsha úlken boladı. Massa deneniń eń tiykarǵı qásiyetlerinen biri.
Tájriybelerdiń kórsetiwinshe formaları birdey, massaları bolsa m1 hám m2 bolǵan denelerdiń hár birine birdey sırtqı kúsh penen tásir etsek, olar alǵan tezleniwler (a1 hám a2) usı denelerdiń massalarına keri proportsional boladı, yaǵnıy
а1 m2 а2 m1
Hár qanday deneniń massası etalon sıpatında qabıl etilgen dene massası menen salıstırıw arqalı ólshenedi. Bul usılda denelerdiń erkin túsiw nızamınan paydalanıladı. Erkin túsiw bolsa denelerge Jerdiń tartıw kúshi tásiriniń nátiyjesi. Jer júziniń hár bir tochkası ushın denelerdiń erkin túsiwidegi tezleniwi turaqlı shama bolıp, g=9,8 m/s2 ǵa teń hám massası m bolǵan denege R = mg shamadaǵı kúsh tásir etedi. Tarezi pállesine qoyılǵan dene pálleni awırlíq kúshine teń kúsh penen basadı. Sol sebepli eki dene massalarınıń qatnası olardıń awırlíqlarınıń qatnasınday boladı:
m1 1 m2 2
Dene massası skalyar shama bolıp, onıń awırlıǵı bolsa vektor shama. Bul vektor erkin túsiw tezleniwi baǵıtında Jerdiń orayína qarap baǵıtlanǵan.
18
Tájriybelerdiń kórsetiwinshe, massa additiv shama, yaǵnıy dene massası onıń bólekleriniń massalarınıń jıyındısına te4. Mexanikalíq sistemanıń massası sistemanıń quramına kiriwshi barlíq deneler massalarınıń jıyındısına te4.
Denege basqa deneler tásir etpese ol erkin dene delinedi. Biraq tábiyatta erkin deneler joq, sebebi tábiyiy sharayatta hár qanday dene basqa deneler tásirinde boladı.
Nyutonnıń birinshi nızamın qanaatlandıratuǵın sanaq sistemaları inertsial sanaq sistemaları delinedi. Basqacha aytqanda, inertsial sanaq sisteması dep sonday sanaq sistemasına aytıladı, onda erkin dene tınısh halatta boladı yaki turaqlı tezlik penen tuwrı sızıqlı qozǵalısta boladı. Bunnan sonday juwmaq shıǵadı, eger bazı bir inertsial sistemasın tańlap alǵan bolsaq, ol halda oǵan salıstırǵanda tuwrı sızıqlı teń ólshewli qozǵalısta bolǵan basqa sanaq sistemaları hám inertsial sanaq sisteması boladı.
2. NYUTONNIŃ BIRINSHI NIZAMI
İngliz fizigi İsaak Nyutonnıń "Natural filosofiyanıń matematikalíq tiykarlari" (1687 j.) degen miynetinde dinamika nızamları bayan etilgen.
Eger denege basqa deneler tásir etpese, ózinıń tınıshlíqtaǵı halatın yaki qozǵalıstaǵı halatın saqlaydı.
Deneni tınısh yaki qozǵalıstaǵı halatın sırtqı kúshler tásir etpegende saqlaw qásiyeti, deneniń inertligi delinedi. Sonıń ushın da Nyutonnıń I nızamın inertsiya nızamı dep te aytıladı.
Nyutonnıń birinshi nızamınıń durıslıǵı tájriybelerden alınǵan nátiyjelerdi ulıwmalastırıwdan kelip shıǵadı.
Nyuton nızamları orınlanatuǵın sistema inertsial sanaq sisteması delinedi. Bul sistema basqa inertsial sistemaǵa salıstırǵanda tınısh halatta yaki tuwrı sızıqlı teń ólshewli qozǵalısta bolıwı kerek. Koordinata bası Quyashta, kósherleri juldızlarǵa qarap ketgen geliotsentrik sistema inertsial sanaq sisteması boladı. Bul sistemada Nyutonnıń birinshi nızamı anıq orınlanadı.
Tájriybelerden bizge belgili, turaqlı kúsh tásirinde turli deneler túrlishe tezleniwler aladı. Deneler alǵan tezleniw deneniń qásiyetine (onıń massasına) baylanıslı boladı.
3. NYUTONNIŃ EKINSHI NIZAMI
Deneniń massasımateriya qásiyetin xarakterlewshi fizikalíq shama bolıp, ol deneniń inertligi hám gravitatsion qásiyetin ańlatadı. Dene tezligin ózgertip, oǵan tezleniw beretuǵın vektor shamaǵa kúsh delinedi.
Materiallíq tochkanıń mexanikalíq qozǵalısınıń sırtqı kúshler tásirinde qanday ózgeriwi dinamikanıń tiykarǵı - ekinshi nızamında bayan etiledi. Qálegen bazı bir denege F1, F2,... kúshler tásir etse, bul kúshler tásirinde dene sáykes ráwishte a1, a2,..., tezleniwler aladı. Biraq F1/a1 = F2/a2 = .... = sonst bolıp, bul shama dene inertligin ańlatadı. Eger turli kúshler bazı bir denege tásir etse, dene alǵan tezleniw kúshlerdiń teń tásir etiwshisine tuwrı proportsional boladı, yaǵnıy
a F (m = const) |
(3.1) |
Eger turli massalı denelerga birdey kúsh tásir etse, deneler alǵan tezleniwler túrlishe boladı. Deneler massaları qansha úlken bolsa, olar alǵan tezleniwler sonsha kishi boladı.
19

a |
|
1 |
|
(3.2) |
||
m |
||||||
|
|
|||||
1 hám 2 teńliklerden |
|
|
|
|
||
a k |
|
F |
(3.3) |
|||
|
m |
|||||
|
|
|
|
|||
jazamız. 3-teńlik Nyutonnıń ekinshi nızamın ańlatadı. Bul ańlatpaga muwapıq, deneniń alǵan tezleniwi kúshke tuwrı, dene massasına keri proportsional boladı. Nyutonnıń ekinshi nızamı inertsial sanaq sisteması ushın orınlı boladı. Birinshi nızam Nyutonnıń ekinshi nızamınıń dara jaǵdayı sıpatında qaraladı. Sistemaǵa qoyılǵan kúshlerdiń teń tásir etiwshisi nolge teń bolǵanda, dene alǵan tezleniwde nolge teń boladı.
Xalíqara birlikler sistemasın(Sİ)da 3-teńliktegi proportsionallíq koeffitsenti k = 1 bolǵanı
ushın
|
a |
F |
|
|
|
||
m |
|
|
|||||
|
|
|
|
|
|||
yaki |
|
|
|||||
|
|
|
dV |
|
|||
F ma m |
|
|
(3.4) |
||||
|
|||||||
|
|
|
dt |
|
|
||
boladı. Dene massası klassikalíq mexanikada turaqlı bolǵanı ushın 4 - teńlikti: |
|||||||
F |
d (mV ) |
|
|
(3.5) |
|||
dt |
|
||||||
|
|
|
|||||
túrinde jazıw mumkin. Materiallíq tochka massasınıń tezligine |
kóbeymesi onıń qozǵalıs |
||||||
muǵdarın (impulsin) belgileydi, yaǵnıy |
|
|
|||||
R = mV |
|
(3.6) |
|||||
Bu teńlikti (3.5)-ge qoyıp |
|
|
|||||
F = dR/dt |
|
(3.7) |
|||||
teńligin payda etemiz. 7-teńlik Nyutonnıń ekinshi nızamınıń ulıwma |
kórinisin ańlatadı. (3.7)- |
||||||
ańlatpa boyínsha denege tásir etiwshi kúsh impulstan waqıt boyínsha alınǵan birinshi tártipli tuwındıga teń eken.
4. NYUTONNIŃ ÚSHINSHI NIZAMI
Nyutonnıń III-nızamına muwapıq eki dene arasındaǵı ózara tásir kúshleri muǵdar jaǵınan teń baǵıtı jaǵınan qarama-qarsı boladı, yaǵnıy
F1 = F2 (3.8) Máselen, massaları m1 hám m2 bolǵan turli belgidegi zaryadlanǵan eki deneni kóreyik (1- súwret). F1 hám F2 kúshler tásirinde deneler a1 hám a2 tezleniwler aladı. Nyutonnıń ekinshi
nızamına muwapıq
F1 m1 a1 |
hám F2 m2 a2 |
(3.9) |
(3.8) hám (3.9)-teńliklerden
m1 a1 m2 a2
yaki
a1 m2 a2 m1
20
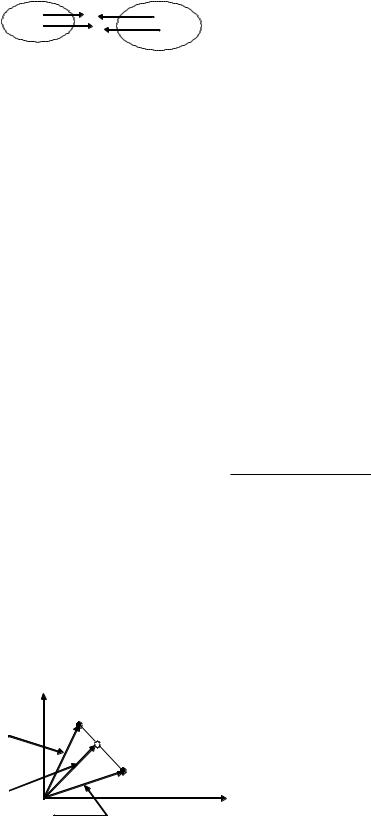
F1 |
F2 |
|
yaǵnıy ózara tásirlesiwshi deneler tezleniwleri olardıń |
|
|
massalarına keri proportsional bolıp, qarama-qarsı tárepke |
|
m1 |
|
m2 |
|
a1 |
a2 |
|
baǵıtlanǵan boladı. |
1-su'wret
5. MASSA ORAYÍ. MASSA ORAYÍNIŃ QOZǴALISI HAQQINDAǴI TEOREMA
Kóp jaǵdaylarda bir neshe deneden (materiallíq tochkalar) ibarat mexanikalíq sistemanıń qozǵalıs nızamların úyreniw menen jumıs alıp barıwǵa tuwra keledi. Bunday sistemanıń qozǵalıs nızamların úyreniwde usı sistema quramındaǵı denelerdiń onda qanday bólistirilgenligin yaki bul deneler bir-birine salıstırǵanda sistemada qanday jaylasqanlıǵın biliw zárúrligi tuwıladı. Usı sebep penen inertsiya orayí (massa orayí) degen túsinik (inertsiya orayí hám massa orayí atamaları bir mániste qollanıladı, sebebi deneniń massası onıń inertsiyasınıń ólshemi) kiritiledi.
İnertsiya orayí hám awırlíq orayí degen túsinikler arasında tómendegishe parıq barlıǵın esten shıǵarmaw kerek: awırlíq orayí-bir tekli awırlíq kúshi maydanında jaylasqan qattı deneler ushın ǵana mániske iye; inertsiya orayí bolsa hech qanday maydan menen baylanıslı emes hám qálegen mexanikalíq sistema ushın orınlı. Awırlíq kúshi maydanında jaylasqan qattı deneler ushın inertsiya orayí hám awırlíq orayí bir-biri menen sáykes túsedi, yaǵnıy bir tochkada jaylasqan boladı. İnertsiya orayí massanıń bólistiriliwin súwretlewshi geometriyalíq tochka bolıp, onıń ornı koordinatalar basına salıstırǵanda rc radius-vektor menen tómendegishe
anıqlanadı.
rc mi r1 m2 r2 ... mn rn , m1 m2 ... mn
yaǵnıy:
rc |
1 |
mi ri , |
(3.10) |
|
m |
||||
|
i |
|
bunda mi - sistemaǵa tiyisli i-deneniń massası; ri - koordinatalar basına salıstırǵanda i-deneniń halatın anıqlawshı radius-vektor; m = m1 + m2 + ... + mn - sistemanıń ulıwma massası.
Ápiwayılastırıw maqsetinde eki denedan ibarat sistemani alıp qarayıq (2-súwret). Massaları m1 hám m2 bolǵan denelerdiń orınları koordinata basına salıstırǵanda sáykes ráwishte r1 hám r2 radiusvektorlar menen berilgen bolsa, bul eki deneden ibarat sistemanıń inertsiya
|
|
Y |
|
|
|
|
|
|
orayí |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
m1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m1r1 |
m2 r2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
rc |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
m |
|
|
||||||
|
r1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
m2 |
|
|
|
formula arqalı ańlatılıp, eki deneniń |
|||||||||
|
|
|
|
|
|
|
|
|
geometriyalíq orayların biriktiriwshi tuwrı |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
rс |
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
sızıqta jatadı. |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
r2 |
|
|
|
|
2-su'wret |
|
|
(10) teńleme vektor arqalı ańlatılǵan |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
teńleme, biraq |
inertsiya oraylarınıń halatın |
anıqlawshı usı |
radius-vektordı onıń koordinata |
|||||||||||||||||||
kósherlerindegi proektsiyaları arqalı da ańlatıw mumkin: |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
X c |
1 |
mi xi , Yc |
|
1 |
mi yi , Zc |
|
1 |
mi zi , |
|
(3.11) |
|||
|
|
|
|
|
|
m |
m |
m |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
i |
|
i |
|
i |
|
|
|
|
|
|||
21
