
Fizika pani boyinsha lekciyalar
.pdf
= BH/ǵ = |
1 |
|
|
H2 |
(11.12) |
|
2 |
0 |
|||||
|
|
|
|
|||
|
|
|
|
|
shama menen ańlatıladı.
Bekkemlew ushın sorawlar:
1.İnduktsion toktıń payda bolıw sebeplerin túschindiriń
2.Lents qádesin aytíń.
3.İnduktsion E№K payda bolıwın energiyanıń saqlanıw nızamına tiykarlanıp túsindiriń.
4.Ózlikinduktsiya hám óz-ara indkutsiya hádiysesin túsindiriń.
5.Katushkanıń indkutivligi neni sıpatlaydı ?
24-tema. Elektr hám magnit maydanlarınıń óz-ara aylanısı.
Jobası:
1.Elektromagnit induktsiya hádiyseleriniń Faradey-Maksvell analizi. Jıljıw togı. Yirimili elektr maydanı.
2.Maksvell teńlemeleri sistemasınıń integral hám differentsial kórinisi.
3.Elektromagnit tolqınlardıń taralıw tezligi. Elektromagnit tolqın teńlemesi. Energiya tıǵızlıǵı. Energiya aǵımınıń tıǵızlıǵı.
Tayanısh sóz hám túsinikler: magnitoelektrlik induktsiya, elektromagnit induktsiya, jıljıw togı, zaryadlardıń bet tıǵızlıǵı, ótkiziwsheńlik togı hám tıǵızlıǵı, elektr induktsiya vektorı, induktsion E№K, yirimli elektr maydan, yirimli tok (Fuko tokları), Maksvell teoriyası, tolíq tok tıǵızlıǵı, elektromagnit tolqin teńlemesi, energiya tıǵızlıǵı, energiya aǵımı tıǵızlıǵı, UmovPoynting vektorı.
Magnitoelektr induktsiya |
elektromagnit induktsiyasıǵa keri bolǵan hádiyse bolıp, onı |
áhúq jılı Maksvell óz gipotezası |
arqalı kórsetti. Elektr maydanınıń ózgeriwi hám bul ózgeriw |
sebepli payda bolıp atırǵan magnit maydan arasındaǵı muǵdarlíq baylanıstı tabıw uchun
Maksvell jıljıw togı dep atalatuǵın túsinikti kiritti. Bul túsinikti tómendegi tájiriybede
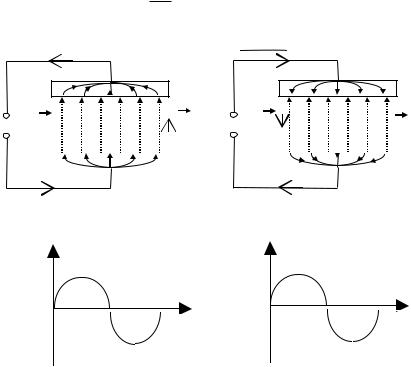
úyrenemiz(á-suwret). Kondensatorlı shınjırdan kvazistatsionar ózgeriwshi tok ótkende kondensator plastinkaların birlestiriwshi ótkizgishler arqalı zaryad ótedi, biraq plastinkalar aralıǵındaǵı dielektrikten ótpeydi. Nátiyjede ózgeriwshi toktıń shınjır boylap aǵıwı kondensatordıń zaryadlanıwı (áa-suwret) hám razryadlanıwınan ibarat boladı (áb-suwret).
Solay etip, ótkiziwsheńlik togınıń sızıqları kondensator plastinkalarınıń bir-birine qaraǵan betlerinde úzilip qaladı. Maksvell bul pikirge qarama-qarsı bolǵan ideyanı ilgeri súrdi. Onıń pikirinche hár qanday ózgeriwshi tok shınjırları hám tuyıq boladı. Tek shınjırdıń ótkizgish bolmaǵan bóleklerinde, yaǵnıy kondensator plastinkalari aralıǵında "jıljıw togı" dep atalatuǵın tok aǵadı. Onı tómendegishe túsinemiz. Shınjırdan ótip atırǵan toktıń bir zamattaǵı mánisi I bolsın. Usı momentte kondensator plastinkalarındaǵı zaryad muǵdarın q dep, olardıń bet
tıǵızlıǵın bolsa Sq dep belgileyik.Ol jaǵdayda kondensator plastinkaları ishindegi ótkiziwsheńlik togı tıǵızlıǵınıń mánisi
142
|
J |
|
dq |
|
1 |
|
d q |
|
d |
|
|
|||
j= |
|
|
|
|
|
|
|
|
. |
(13.á) |
||||
|
|
|
|
|
|
|||||||||
|
S |
|
dt |
|
S |
|
dt |
S |
|
dt |
|
|
||
Usı momentte plastinkalar aralıǵındaǵı elektr maydan kernewliliginiń mánisi E |
|
ǵa |
|||
|
|||||
0 |
|||||
te4. Maydannıń elektr induktsiyası bolsa |
|
|
|
|
|
D 0 E 0 |
|
. |
(13.ǵ) |
|
|
|
|
|
|||
|
|
|
|||
|
|
|
|
|
|
|
0 |
|
|
|
|
?aqıt ótiwi menen plastinkalardaǵı zaryadtıń bet maydan induktsiyası mánisiniń ózgeriwine sebep boladı.
D d
t dt
tıǵızlıǵı ózgeredi. Bul bolsa elektr
(13.q)
|
D |
|
|
|
D |
|
D |
|
|
|
|
|
||||
|
|
|
|
tt |
|
t |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
I |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Iу |
|
|
|
|
|
Iу |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
||
|
|
а) |
|
|
|
|
|
|
б) |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
á-suwret |
|
|
|
|
|
|
|
|||
Kondensator zaryadlanıp atırǵan |
waqıtta |
(áa-suwret) plastinkalar |
aralıǵındagı |
elektr |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
dD |
|
|
|
|
|
|
|
|
|
|
|||
maydan kúsheyip baradı. Bul waqıtta |
|
vektor D |
vektorǵa parallel |
bolıp, onıń |
baǵıtı |
|||||||||||
|
|
|
||||||||||||||
dt |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
shınjırdaǵı ótkiziwsheńlik togınıń baǵıtı menen birdey boladı. Kerisinshe, razryadlanǵanda (áb-
suwret) elektr maydan tómenlep baradı. Bul jaǵdayda |
elektr |
induktsiya vektorınıń ózgeriw |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
dD |
|
|
|
dD |
|
|
|
||||
tezligin |
ańlatıwshı |
vektor D ǵa anti parallel. Biraq |
|
vektordıń baǵıtı ótkiziwsheńlik |
|||||||||
dt |
dt |
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
togınıń |
baǵıtı menen birdey. Demek, barlíq waqıtta |
|
dD |
nıń baǵıtı ótkiziwsheńlik togınıń baǵıtı |
|||||||||
|
dt |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
menen birdeyboladı. (13.á) hám (13.q) ańlatpaların |
salıstırsaq |
dD |
nıń hám ótkiziwsheńlik togı |
||||||||||
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
dt |
||
tıǵızlıǵınıń mánisleri óz-ara teńligini kórsetedi. |
dD |
|
nıń birligi |
|
|
||||||||
dt |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
143

dD |
|
K‘ |
|
1 |
A |
|||||
|
|
|
|
M |
2 |
|
C |
|
M |
2 |
dt |
|
|
|
|
||||||
Demek, dD hám tok tıǵızlıǵınıń ólshem birliginde ólshenedi. dt
gipotezası boyınsha jıljıw togınıń tıǵızlıǵı dep ataladı: |
|
|||||
|
|
|
|
|
||
|
|
dD |
|
(13.ń) |
||
j |
|
|
||||
–ЏЏ |
dt |
|||||
|
|
|
||||
|
|
|
|
|||
dD shama, Maksvell dt
Solay etip, ózgeriwshi tok shınjırında ótkizgishlerdegi ótkiziwsheńlik togınıń sızıqları kondensator plastinkaları aralıǵındaǵı jıljıw togınıń sızıqlarına jalǵanıp ketedi. Jıljıw togı hám ótkiziwsheńlik togına uqsas keńislikte yirimli magnit maydanın payda etedi. №ozǵalmas kontur
menen shegaralangan bet |
arqalı |
ótiwshi |
magnit |
maydanınıń ózgeriwi |
magnit |
induktsiya |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
vektorınan waqıt boyínsha |
alınǵan |
tuwındı |
|
dB |
arqalı xarakterlenedi. Konturda payda bolıp |
|||||||||
|
dt |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
atırǵan induktsion elektr qozǵawshı kúshti hám |
dB |
arqalı ańlatıw mumkin. Kontur beti S den |
||||||||||||
dt |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
ótiwshi F magnit aǵımı magnit maydan induktsiyası V arqalı |
|
|
||||||||||||
|
|
|
F= BndS |
|
|
|
|
|
|
|||||
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
formada anıqlanıwınan paydalanıp induktsion elektr qozǵawshı |
kúshtiń |
ańlatpasın |
||||||||||||
tómendegishe jazamız: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
d |
|
|
|
|
dB |
|
|
||||
ind= |
|
|
|
B dS |
|
|
dS |
(13.ó) |
|
|||||
|
|
|
|
|
||||||||||
|
dt |
|
dt |
S |
n |
|
|
S |
dt S |
|
|
|||
Magnit maydanınıń ózgeriwi nátiyjesinde keńislikte induktsion elektr maydan payda boladı
hám ol ótkizgishtegi erkin elektronlardı tártipli háreketke keltiredi, degen juwmaqqa kelemiz. |
|
|
|
Bul maydan kernewlilik vektorı E B nıń tuyıq kontur |
boyínsha tsirkulyatsiyası usı konturda |
payda bolıp atırǵan induktsion elektr qozǵawshı kúshke teń: |
|
ind= E B dl |
(13.ú) |
l |
|
Bul ańlatpa ózgeriwshi magnit maydanınıń sebebinen payda bolıp atırǵan elektr maydanınıń kernewlilik sızıqları, qozǵalmas zaryadtıń elektr maydanınıń kernewlilik sızıqlarınan
ózgeshelenip, tuyıq |
bolatuǵınlıǵınan derek beredi. |
Basqacha |
aytqanda, |
induktsion elektr |
||
|
|
|
|
|
|
|
|
|
|
|
dB |
|
|
maydan, magnit maydanı sıyaqlı yirimli hárakterge iye |
boladı. |
E B sızıqları |
|
menen shep |
||
|
dt |
|||||
|
|
|
|
|
|
|
vint qádesi tiykarında |
baylanısqan (ǵ-suwret). |
|
|
|
|
|
|
В |
|
В |
|
|
|
|
Е |
B |
0 |
Е |
t |
|
B 0t
144

ǵ-suwret
Sonıń uchın ádette bul maydan yirimli elektr maydanı dep ataladí. Yirimli elektr maydanı keńisliktiń úyrenilip atırǵan bóleginde kontur bolıwı yamasa bolmaslıǵınan qáttiy názer payda boladı. Biraq bul maydannıń payda bolıwı uchın ózgeriwshi magnit maydan bolıwı shárt. (13.ó) hám (13.ú) ti teńlestiriw nátiyjesinde:
|
|
dB |
|
|
||
E B l dl |
|
|
dS |
(13.w) |
||
|
||||||
l |
S |
|
dt n |
|
||
|
|
|
|
|
|
|
ni payda qılamız.
Solay etip, ózgeriwshi magnit maydanı sebepli payda bolatuǵın yirimli elektr maydan kernewliliginiń ıqtıyarıy tuyıq kontur boyínsha tsirkulyatsiyasi magnit induktsiya vektorınıń
waqıt dawamında ózgeriwin xarakterlewshi ddtB vektordı usı kontur shegaralaǵan ıqtıyarıy bet
arqalı aǵımınıń keri belgi menen alınǵan mánisine teń boladı. Keńisliktiń yirimli elektr maydan payda bolǵan bólegine bir tekli ótkizgish bólekshesi jaylastırılsa hám yirimli toklar payda boladı. Bunday yirimli toklar Fuko tokları dep ataladí.
Maksvell jıljıw togı túsinigin qollap elektr hám magnit hádiyseleriniń jalǵız teoriyasın jarattı. Maksvell teoriyasınıń tiykarın tórt teńleme quraydı.
á) №ozǵalmas zaryad q óz dógeregindegi keńislikte elektr maydanın payda etedi. Bul
maydan potentsial maydan. Sonıń uchun bul maydan kernewlilik vektorı Eq niń ıqtıyarıy tuyıq
kontur boyínsha tsirkulyatsiyasi (yaǵnıy elektrostatik maydan kúshleriniń tuyıq jolda orınlaǵan jumısı) nolge teń:
|
|
|
Eq d =0 |
|
|
(13.h) |
|||
Yirimli elektr |
maydan kernewliligi |
|
|
|
vektordıń ıqtıyarıy tuyıq kontur boyínsha |
||||
E B |
|
||||||||
tsirkulyatsiyasi (13.w) ge tiykarlanıp nolden ózgeshe: |
|
||||||||
|
|
|
dB |
|
|
|
|||
|
|
EB d |
|
|
|
|
dS |
(13.9) |
|
|
|
|
|
|
|||||
|
|
|
|
dt n |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ulıwma jaǵdayda elektr maydan Eq |
hám |
E B |
maydanlarınıń jıyındısıdan ibarat bolıwı |
||||||
|
|
|
|
|
|
|
|
|
|
mumkin, yaǵnıy E = Eq + E B dep belgilep, (13.h) |
|
hám |
(13.9) teńlemelerin qossaq: |
||||||
|
|
El dl |
dB |
|
|
||||
|
|
|
|
|
dS |
(13.10) |
|||
|
|
|
|||||||
|
|
l |
|
dt |
n |
|
|||
|
|
|
|
|
|
|
|
|
|
Maksvelldiń integral kórinisindegi birinshi teńlemesi kelip shıǵadı. (13.10)nıń shep tárepindegi integral ıqtıyarıy tuyıq kontur boyínsha, oń tárepindegisi bolsa usı kontur shegaralap turǵan ıqtıyarıy bet boyınsha alınadı.
ǵ) Hár qanday elektr togı dógereginde magnit maydanı payda boladı. Magnit maydan r
kernewliligi vektorı H tıń ıqtıyarıy tuyıq kontur boyínsha tsirkulyatsiyasi usı kontur orap alǵan barlíq makroskopik toklardıń algebrik jıyındısına teń:
H l dl |
J jn dS |
(13.áá) |
l |
S |
|
145

|
ózgeriwshi elektr maydan tok sıyaqlı |
|
magnit maydanın payda etedi. Demek, ulıwma |
|||||||||||||||||
jaǵdayda magnit maydan ótkiziwsheńlik togı |
|
j y hám jıljıw togı jc sebepli payda bolǵan magnit |
||||||||||||||||||
maydanlardıń jıyındısınan ibarat. Eger ótkiziwsheńlik togı |
|
tıǵızlıǵı hám jıljıw togı tıǵızlıǵı |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dD |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
j = |
|
lardıń jıyındısınan ibarat bolǵan tolíq tok tıǵızlıǵı |
j |
Т |
: |
|||||||||||||||
|
||||||||||||||||||||
c |
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
dD |
|
|
|
|||||||||
|
|
j |
Т |
= |
j |
y |
+ |
j = |
j |
y |
+ |
|
|
|
|
|
|
|
(13.12) |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
c |
|
|
|
|
dt |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
túsiniginen paydalansaq, (13.áá) ti tómendegishe jazıw mumkin: |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H d |
|
|
dD |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
(13.áq) |
||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
j y |
|
dt |
|
dS . |
|
|
||||||||||||
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Bul ańlatpa Maksvelldiń ekinshi teńlemesi dep atalib, ol magnit maydan kernewlilik vektorı
H tıń ıqtıyarıy tuyıq kontur boyínsha tsirkulyatsiyası usı konturǵa tirelgen ıqtıyarıy S bet arqalı
ótiwshi makroskopik hám jıljıw toklarınıń algebrik jıyındısına teńligini kórsetedi.
q) Elektr induktsiya vektorı D nıń ıqtıyarıy tuyıq bet arqalı aǵımı usı bet ishindegi barlíq erkin zaryadlardıń algebraik jıyındısına teń:
|
DndS dV , |
(13.áń) |
|
|
|
|
S |
V |
|
|
|
bunda - tuyıq |
bet ishinde |
úzliksiz túrde |
jaylasqan zaryadlardıń |
kólemlik |
tıǵızlıǵı. |
Maksvelldiń úshinshi |
teńlemesi dep atalatuǵın (13.áń) teńleme qozǵalmas |
zaryadlar |
sebepli |
||
payda bolǵan potentsial elektr maydan hám ózgeriwshi magnit maydan sebepli payda bolǵan yirimli elektr maydanlar jıyındısınan quralǵan elektr maydan uchın hám orınlı.
ń). Magnit maydan qanday usul menen payda bolǵanlıǵınan qáttiy názer magnit induktsiya sızıqları barlíq waqıtta tuyıq boladı. Sonıń uchın ulıwma jaǵdayda
|
BndS 0 |
(13.áó) |
|
|
|
S |
|
|
|
Bul ańlatpa V vektor uchın Gauss teoreması. Onı |
Maksvelldiń tórtınshi teńlemesi dep |
|||
ataymız. |
|
|
|
|
(13.10),(13.áq),(13.áń),(13.áó)teńlemeleri integral kórinisindegi Maksvell teńlemeleri |
||||
bolıp tabıladı.. |
|
|
|
|
Maksvell teńlemeleri Nyuton mexanıkasınıń nızamları, termodinamika bas nızamları |
||||
sıyaqlı úlken áhemiyetke |
iye bolǵan tábiyat nızamları. Maksvell teoriyasınıń |
eń |
tiykarǵı |
|
|
|
r |
r |
|
nátiyjeleriden biri elektromagnit tolqınlardıń kóldeneń tolqınlar ekenligi. E hám |
H |
vektorlar |
||
|
r |
|
|
|
óz-ara perpendikuyar bolıp, olar tolqınnıń taralıw tezligi V |
ǵa perpendikulyar tegislikte jatadı. |
|||
Elektromagnit tolqındı eki |
óz-ara perpendikulyar tegisliklerde jatıwshı sinusoidalar formaida |
|||
suwretlew mumkin (q-suwret). |
|
|
|
|
146

Y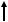
r |
|
r |
|
r |
|
|
E |
|
|
E |
|
r |
|
|
H |
|
|
|||
|
|
|
|
|
||
|
|
|
|
|
V |
|
|
|
|
|
|
|
0
|
|
|
|
X |
|
Z |
|
|
|
|
|
r |
r |
r |
|
|
|
H |
|
|
|||
E |
H |
|
|
||
|
|
|
|||
|
|
q-suwret |
|
|
|
Sinusoidalardan biri elektr maydan |
kernewlilik vektorı |
nıń, ekinshisi bolsa magnit |
|||
E |
|||||
|
|
|
|
|
|
maydan kernewlilik vektorı H tıń terbelislerin sıpatlaydı. Elektromagnit tolqın chastotası birdey saqlansa (=const), onı monoxromatik elektromagnit tolqın dep ataymız. OX kósheri
baǵıtında tarqalıp atırǵan chastotalı elektromagnit tolqın tómendegishe jazıladı: |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E = E msin( t-kx+0), |
|
|
(13.ǵq) |
||
|
|
|
|
H = H msin( t-kx+0). |
|
|
(13.ǵń) |
||
|
|
|
|
|
|
|
|
||
Bunda |
E m |
hám |
H m- |
sáykes túrde |
E |
hám |
H vektorlardıń amplituda mánisleri, |
||
k= /V=ǵ/ -tolqın sanı, 0 - koordinatası x=0 tochkadaǵı terbelislerdiń dáslepki fazası. Elektromagnit tolqınnıń differentsial teńlemesi tómendegishe boladı:
|
2 E |
|
2 E |
|
2 E |
|
1 2 E |
(13.ǵó) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
x 2 |
|
y2 |
|
z2 |
V 2 t 2 |
|||||||||
|
|
|
|
|
|
|
|||||||||
2 H |
|
2 H |
|
2 H |
|
|
1 2 E |
(13.ǵú) |
|||||||
x 2 |
|
y2 |
|
z2 |
|
V 2 |
t 2 |
||||||||
|
|
|
|
|
|
|
|||||||||
Bunda V - elektromagnit tolǵınnıń fazalíq tezligi.
Maksvell teoriyasına tiykarlanıp, elektromagnit tolqınnıń birar ortalíqta tarqalıw tezligi usı ortalíqtıń elektr hám magnit qásiyetlarine baylanıslı bolıp, onıń mánisi:
V= |
1 |
. |
(13.ǵw) |
0 0 |
Vakkumda ortalíqtıń magnit sińiriwshiligi hám dielektrik sińiriwshiligi birge teń hám elektromagnit tolqınlardıń maksimal tarqalıw tezligi:
C |
|
1 |
|
|
|
3.10h m/s. |
(13.ǵh) |
|
|
|
|
|
|
||||
|
|
|
|
|
||||
0 |
|
0 |
||||||
|
|
|
|
|
Bunnan paydalanıp teńlemeni tómendegishe jazamız:
|
|
|
V |
|
C |
|
|
C |
. |
(13.ǵ9) |
|
|
|
|
|
|
|
||||
|
|
|
|
|||||||
|
|
|
|
|
|
|
n |
|
||
|
|
Demek, elektromagnit |
tolqınnıń |
ortalíqta |
tarqalıw tezligi vakkumdaǵı tezlikten n |
|||||
|
|
|
|
|
||||||
= márte kishi (n-ortalíqtıń |
sındırıw |
kórsetkishi). Birlik kólemdegi elektromagnit maydan |
||||||||
147

energiyası W, |
elektr maydan energiyasınıń tıǵızlıǵı We hám magnit maydan energiyasınıń |
||||||||
tıǵızlıǵı Wm jıyındısınan ibarat: |
|
|
|||||||
|
|
|
W=We+WM=0 Eǵ /ǵ + 0Hǵ/ǵ, |
|
(13.q0) |
||||
bunda We=Wm ekenliginen paydalansaq (13.q0) ti tómendegishe jazamız: |
|||||||||
|
|
|
W= ǵWe = ǵWM= 0 Eǵ = 0Hǵ |
. |
(13.qá) |
||||
|
|
|
|
|
|
|
|
||
Bunnan |
|
0 E 0 H degen juwmaqqa kelemiz. Bul bolsa (13.qá) ańlatpanı |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W= 0 0 EH |
|
(13.qǵ) |
|||
kórinisinde jazıwǵa imkan beredi.
Eger (13.ǵw) hám (13.qǵ) larni aǵzama aǵza kóbeytsek, birlik waqıtta birlik bet arqalı
kóshirilip atırǵan energiya aǵımınıń tıǵızlıǵın |
|
||
S = W. V = E. N |
(13.qq) |
||
kórinisinde ańlatamız. Bu ańlatpanı vektor kórinisinde tómendegishe jazsa boladı: |
|||
|
|
|
|
S = [ E |
H ] |
(13.qń) |
|
ádette S vektorı Umov-Poynting vektorı dep ataladı.
Bekkemlew ushın sorawlar.
1.Maksvell teńlemeleri elektromagnitizmnıń qaysı nızamların sıpatlaydı?
2.Jıljıw togı ne?
3.Maksvell teńlemeleriniń integral hám differentsial formaların jazı4.
4.Elektromagnit vektorlar uchın Lorentts almastırıwları qanday?
5.Umov-Poyting vektorın túsindiriń.
6.Elektromagnit tolqınlardıń tarqalıw tezligi nelerge baylanıslı?
7. Yirimli elektr maydanın aytıp beriń.
4-MODUL. OPTIKA. GEOMETRIYALÍQ OPTIKA
25-tema. Jaqtılíqtıń tábiyatı.
Jobası:
1.Jaqtılíqtıń tuwrı sızıqlı tarqalıwı. Jaqtılíqtıń shaǵılısıw hám sınıw nızamları.
2.Nurlardıń úshmúyeshli prizmadaǵı jolı. Linzalar. Linzanıń optikalíq kúshi hám formulası.
Optikalíq ásbaplar.
3.Jaqtılíq difraktsiyası hám interferentsiyası
4.Fotoeffekt hádiysesi
Jaqtılíqtıń tarqalıwı. Ádep jaqtılíqtıń qásiyeti ne - degen soraw bizdi qızıqtıradı. İnsan sezetuǵın jaqtılíq - tolqın uzınlıǵı = (0,38 – 0,77) ·10-6 m intervalda bolǵan elektromagnit tolqınlar. Biraq bunday juwap keyingi waqıtlarda alınǵan tájiriybe nátiyjelerine sáykes kelmey qaldı. Tájiriybeler nátiyjesine qarap, jaqtılíqta bólekshelerdiń aǵımına sáykes qásiyeti bar ekenligi anıqlandı.
Endi jaqtılíqtıń tarqalıwına baylanıslı bazıbir qásiyetler - jaqtılíq-tıń tuwrı sızıq boylap tarqalıwı menen tanısamız.
148

Jaqtılíq nurı degende energiya aǵımınıń tarqalıw baǵıtı názerde tutıladı. Tájiriybe hám baqlawlardan anıqlanıwınsha, bir tekli ortalíqta jaqtılíq tuwrı sızıq boylap tarqaladı eken. Bir tekli ortalíqta jaqtılíq nurları tuwrı sızıqlardan ibarat boladı.
Ólshemi júdá kishi jaqtılíq deregi S ten tarqalıwshı jaqtılíq bazıbir ekranǵa tússin. Jaqtılíq jolına bazıbir dene, móldir bolmaǵan shar formadaǵı D dene qoyılsa, ekranda deneniń anıq sayası payda boladı (33a-súwret.).
|
|
Bunda deneniń sayası, yaǵnıy nur túspeytuǵın |
D |
|
ekran betinde anıq shegaraǵa iye bolıp, jaqtılíqtıń |
|
|
tuwrı sızıq boyínsha tarqalı-wın dálilleydi. Eger |
S |
|
jaqtılíq deregi noqatlíq bolmay, belgili ólshemge iye |
a) |
|
bolsa, onda sayanıń anıq shegarası joǵaladı. Dene |
|
||
|
|
formasınıń bazıbir bólimine ekranda saya payda qılıwı |
|
|
|
|
|
múmkin (33 b-súwret.). |
D |
|
Jaqtılíqtıń shaǵılısıw nızamı. Bir tekli ortalíqta |
|
|
tuwrı sızıq boylap tarqalıp atırǵan jaqtılíq nurı óz |
S |
|
jolında birinshi ortalíq penen shegaralanǵan ekinshi |
|
||
b) |
|
ortalíqta |
33-súwret.
dus kelse, onıń baǵıtı ózgeredi. Eki ortalíq shegarasınıń qásiyetine baylanıslı ráwishte jaqtılíqtıń belgili bólimi I ortalíqqa qaytadı, qalǵan bólimi bolsa II ortalíqqa ótedi. Jaqtılíqtıń eki ortalíq shegarasınan jáne I ortalíqqa qaytıwı jaqtılíqtıń shaǵılısıwı delinedi.
Mısal ushın bazıbir denege jaqtılíq túsip atırǵan bolsın. Eger dene jaqtılíqtı shaǵılıstırıw qásiyetine iye bolsa hám onıń beti gedir-budır bolsa, túsken nur deneden túrli baǵıtlardan qaytadı hám biz deneni qálegen baǵıtta kóriwimiz múmkin. Jaqtılíqtıń bunday qaytıwı diffuziyalíq yamasa tarmaqlasqan shaǵılısıw delinedi.
|
|
|
|
|
Shaǵılısqan nurlar belgili baǵıtqa iye bolıwı |
|
|
|
|
|
ushın ortalíqlardıń shegarası, shaǵılıstırıwshı |
|
|
|
|
|
deneniń beti tegis bolıwı kerek. Beti optikalíq |
|
|
|
|
|
jaqtan tegis bolıwı ushın ondaǵı gedir |
|
|
|
|
|
budırlíqlardıń shaması jaqtılíqtıń tolqın uzınlıǵı |
|
|
|
|
|
0,4 – 0,8 mkm dan kishi bolıwı kerek. Bunday |
a) |
b) |
|
|||
|
|
|
|
|
betlerdi alıw, te- |
34-súwret.
gis shiyshe plastinkanıń betine metall qatlam qaplaw menen ámelge asırıladı.
Jaqtılíqtıń shaǵılısıw qubılısın tájiriybe jolı menen úyreniw nátiyjesinde shaǵılısıw nızamı anıqlanǵan.
. Túsken nur, qaytqan nur hám nurdıń túsiw noqatınan eki ortalíq shegarasıga júrgizilgen perpendikulyar bir tegislikte jatadı.
. Nurnıń túsiw múyeshi qaytıw múyeshine teń boladı = .
Eger jaqtılíq keri baǵıtta, yaǵnıy qaytıw múyeshi menen túsken bolsa, onıń qaytıw múyeshi
ádepki túsiw múyeshine teń boladı.
149

Jaqtılíqtıń sınıw nızamı. Jaqtılíqtıń bir móldir ortalíqqa ótiwi hám bul ótiwde onıń tarqalıw baǵıtınıń ózgeriwi jaqtılíqtıń sınıwı delinedi.
Jaqtılíqtıń sınıwın tekseriw ushın sonday tájiriybe isleyik. Shiyshe tsilindr ıdıs alıp oǵan jatqarılǵan halda yarımına shekem suw quyamız. 35-súwrette kórsetilgen 0 noqat tárep jaqtılíq nurın túsiremiz.
|
|
|
I |
0 |
II |
|
|
35-súwret. |
|
sin = n1 2 sin
Idıstıń arqa tárepine ekran qoyıladı. Bunda I bólimi bizge tanıs bolǵan shaǵılısqan nur, II bólimi bolsa, jaqtılíqtıń ekinshi ortalíq - suwga ótken bólimi.Tekseriwle tiykarında jaqtılíqtıń sınıw nızamı:. Túsiwshi nur, sınǵan nur hám ortalíq shegarasına nurdıń túsiw noqatınan júrgizilgen perpendikulyar bir tegislikte jatadı.
. Túsiw múyeshi sinusınıń sınıw múyeshi sinusina qatnası shegaralasqan ortalíqlardıń optikalíq qásiye tine baylanıslı bolǵan turaqlı shama bolıp, onı ekinshi ortalíqtıń birinshi ortalíqqa salıstırǵandaǵı sındırıw kórsetkishi delinedi, yaǵnıy
(1)
Eger jaqtılíq absolyut sındırıw kursatkishi n1 bolǵan ortalíqtan n bolǵan ortalíqqa ótse, ortalíqlar absolyut sındırıw kórsetkishleriniń qatnası ekinshi ortalíqtıń birinshi ortalíqqa qaraǵandaǵı salıstırmalı sındırıw kórsetkishine teń boladı:
n2 / n1 = n1 2 (2)
Ortalíqtıń absolyut sındırıw kórsetkishiniń mánisi jaqtılíq nurınıń sol ortalíqtaǵı tarqalıw tezligi menen baylanıslı, yaǵnıy ortalíqtıń absolyut sındırıw kórsetkishi jaqtılíq nurınıń vakuumdaǵı tezliginiń ortalíqtaǵı tarqalıw tezligine qatnasına teń:
n = |
c |
|
|
(3) |
|
|
|
|
v |
|
|
|
|
|
|
Nurlardıń |
úshmúyeshli |
prizmadaǵı jolı. |
Prizmalar optikalíq ásbaplardıń |
tiykarǵı |
|||
bólimleriniń biri bolıp, túrli optikalíq qubılıslardı tekseriwde keń qollanıladı. |
|
|
|||||
|
|
|
|
-súwrette úshmúyeshli shiyshe prizmanıń jaqlarına |
|||
|
|
V |
perpendikulyar tegislik menen kesilisiw halı kórsetilgen. |
||||
O / |
|
|
|
Prizmanıń AV hám VS jaqları sındırıwshı jaqlar bolıp |
|||
|
|
|
esaplanadı. |
Olardıń arasındaǵı AVS = |
|
múyesh |
|
|
|
prizmanıń nurdı sındırıwshı múyeshi delinedi. |
|
|
|||
j |
|
|
j/ |
|
|
||
|
|
|
|
||||
|
|
Nurdıń prizmaǵa kelgenshe bolǵan baǵıtı menen onıń |
|||||
O |
|
|
|
prizmadan ótkennen keyingi baǵıtı arasın- |
|
|
|
A |
|
|
S |
|
|
|
|
36-súwret. |
|
|
|
|
|
|
|
daǵı múyesh aǵıw múyeshi delinedi. Súwrette bul múyesh menen belgilengen. Sındırıwshı múyeshi kishi bolǵan, yaǵnıy jaqları bir-birine jaqın jaylasqan «juqa» prizmalar ushın aǵıw múyeshin sındırıwshı múyesh arqalı belgileymiz:
= (n – 1)
formula járdeminde tabıw múmkin.
150

Linzalar. Jaqtılíqtıń sınıw qásiyetlerinen texnikada hám kúndelikli turmısta júdá kóp paydalanıladı. Onı optikalíq linzalar mısalında kóriw múmkin.
Eki tárepi sferalíq bet penen shegaralanǵan móldir dene linza dep ataladı. Sferalíq bet shar
betiniń bir bólimi bolǵanlıǵı ushın onıń iymeklik radiusı |
|
|||||||||
|
|
|
|
|
|
|
|
|
boladı. Sferalíq betlerdiń orayları arqalı ótiwshi |
|
|
|
|
|
|
|
|
|
|
S1S2 tuwrı sızıq linzanıń bas optikalíq kósheri |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
delinedi. |
|
|
R1 |
R2 |
|
|
|
|
|
|
Ortası shetine qaraǵanda qalıńıraq bolǵan |
|
C1 |
|
C2 |
|
|
|
|
linzalar jıynawshı linzalar delinedi. |
Ortası |
||
|
R1 |
R2 |
|
|
|
|
|
shetine salıstırǵanda juqalaw bolǵan linzalar |
||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
shashıratıwshı linzalar delinedi. b-súwrette |
|
|
a) |
|
|
b) |
|
|
v) |
shashıratıwshı, v-súwrette jıynawshı linzalar. |
||
37-súwret. |
|
|
|
|
|
|
|
|
|
|
Linzanıń qalıńlıǵı, deneden linzaǵa shekemgi yamasa linzadan súwretleniwge shekemgi bolǵan aralíqqa salıstırǵanda kishi boladı. Bunday linzalar juqa linzalar delinedi. Linza betin belgilewshi sferalíq segmentlerdiń linza orayíndaǵı ushları juqa linzada bir-birine júdá jaqın jaylasqan. Sol sebepli bir noqat dep esaplaw múmkin. Bul O noqat linzanıń optikalíq orayí delinedi. Linzanıń bas optikalíq kósheri onıń optikalíq orayínan ótedi. Optikalíq oraydan ótiwshi hám bas optikalíq kósherge salıstırǵanda bazıbir múyesh astında baǵıtlanǵan tuwrı sızıq járdemshi optikalíq kósher delinedi.
Eger linzaǵa onıń bas optikalíq kósherine parallel nurlar túsirilse, olar linzadan ótip sınadı hám óz baǵıtın ózgertedi. Linza jıynawshı bolsa, nurlar bir-birine jaqınlasıp bir noqatta kesilisedi. Nurlar kesilisken noqat linzanıń bas fokusı delinedi hám F háribi menen belgilenedi.
Linzanıń fokus aralıǵı qansha kishi bolsa, onıń nurdı sındırıw qábileti sonsha úlken boladı, yaǵnıy sınǵan nur sonsha úlken múyeshke awısadı. Fokus aralıǵı úlken bolǵanda awısıw múyeshi kishi boladı. Linzanıń bunday qásiyetin xarakterlew ushın, fokus aralıǵı ornına keri bolǵan fizikalíq shama kiritiledi. Bul shama linzanıń optikalíq kúshi delinedi hám D menen belgilanadi:
D = |
1 |
(11-4) |
|
F |
|||
|
|
Eger linzanıń fokus aralıǵı m bolsa, onda onıń optikalíq kúshi dioptriyaǵa teń dep esaplanadı, yaǵnıy dptr = /m.
Linza betlerin arnawlı radius mánisine iye bolǵan sharlardıń bir bólimi dep esaplaw múmkin. Onda linzanıń optikalíq kúshin onıń betleriniń R1R2 iymeklik radiusları hám linzanıń absolyut sındırıw kórsetkishi n járdeminde ańlatıw múmkin:
D = (n-1)( |
1 |
|
1 |
) |
(11-5) |
|
|
||||
|
R1 |
R2 |
|
||
Bunda hawanıń sındırıw kórsetkishi ge teń dep qabıl qılınǵan.
Linza formulası. Linza járdeminde alınǵan dene súwreti onıń linzaǵa salıstırǵanda jaylasıwı hám linzanıń optikalíq kúshine baylanıslı bolıp esaplanadı. Ol linza formulası járdeminde tabıladı. Linza formulası úsh shama buyımnan linzaǵa shekemgi d aralíq, linzadan súwretleniwge shekemgi bolǵan f aralíq hám linzanıń F bas fokus aralıǵı arasındaǵı baylanıstı
151
