Fizika pani boyinsha lekciyalar

I

ketedi.

a) Tuwrı toktıń magnit maydanı

Sheksiz uzun, jińishke ótkizgish ózinen R aralíqta jaylasqan birar A tochkada payda etken magnit induktsiya shaması dV nı esaplayıq r = R/cos , dl = r . d /cos

Bul ańlatpalardı 8.h-teńlikka qoyıp tok elementi payda etken magnit induktsiyası shamasın tabamız.

8.9 - teńliktegi múyesh mánisleri 0 dan ge shekem ózgergeni uchun 8.ú hám 8.9 - teńliklerge kóre:

132

8.10-teńlikke kóre, tuwrı tok payda etken magnit induktsiyası shaması tok kúshine proportsional eken.

b) Aylanba tok orayíndaǵı magnit maydanı

Radiusi R bolǵan sheńber formadaǵı ótkizgishten I tok ótip atırǵan bolsın (8.w-suwret).

8.w-suwret

Sheńberdiń hár bir dl elementi hám radiusı R arasındaǵı múyesh /ǵ ge teń bolǵanlıǵı uchun Bio-Savar-Laplas nızamına tiykarlanıp:

Barlíq dB lar birdey baǵıtta, yaǵnıy sheńber orayínan ótiwshi oń normal ( n ) boylap

baǵıtlanǵan. Sonıń uchun juwmaqlawshı maydannıń sheńber orayíndaǵı magnit induktsiyası:

(8.áń) teńlikke kóre dóńgelek toktıń magnit maydanı sheńber formadaǵı toklı konturdıń magnit momentine tuwrı proportsional eken.

Bekkemlew ushın sorawlar.

1.Toklı ótkizgishler jaqınına jaylastırılǵan sınaw ramkalarına qanday kúshler tásir etedi ?

2.Magnit induktsiyası dep nege aytıladı ?

3.Maydanlar supperpozitsiya printsipini túsindiriń.

4.Bio-Savar hám Laplas nızamlarınan maydan indkutsiyası shamasın esaplawda qanday paydalanıladı ?

133

22-tema. Vakkumdaǵı magnitostatikanıń tiykarǵı teńlemeleri

Jobası:

1.Amper nızamı. Parallel toklardıńóz-ara tásiri.

2.Háreketdegi zaryadqa magnit maydanınıń tásiri. Lorents kúshi. Xoll effekti.

3.Magnit maydanında zaryadlanǵan bólekshelerdiń háreketi. Zaryadlanǵan bólekshelerdi tezlestiriwchi qurılmalar (tezletkichler).

Tayanısh sózlar hám túsinikler: Amper kúshi, shep qol qádesi, parallel toklar, Lorents

kúshi, orayǵa umtılıwshı kúsh, Xoll turaqlısı, sızıqli rezonans, tsiklotron, duant.

1. Amper nızamı. Parallel toklardıń óz-ara tásiri.

Magnit maydanda jaylasqan toklı ótkizgishke maydan tárepinen tásir etiwshi kúsh usı maydannıń magnit induktsiyası V ǵa, ótkizgishtiń geometriyalíq ólshemlerine hám onnan ótip atırǵan tok kúshi I ge baylanıslı boladı.

I

alaqanımızǵa kirsin, tórt achılǵan barmaq tok baǵıtına sáykes kelsa, 900 ǵa ashılǵan bosh barmaq Amper kúshiniń baǵıtın kórsetedi.

Amper nızamı tok ótip atırǵan eki parallel ótkizgishlerdiń óz-ara tásir kúshlerin anıqlawda qollanıladı.

Óz-ara parallel, arasındaǵı aralíq R bolǵan Iá hám Iǵ toklar ótip atırǵan(toklar baǵıtı ǵ- suwrette kórsetilgen) sheksiz uzınlíqtaǵı toklı ótkizgishlerdi kórip óteyik.

Iә I2

Bә

dF 134

dF

ǵ- suwret

Hár bir ótkizgish óziniń dógereginde magnit maydanın payda etedi hám usı maydan arqalı Amper nızamına kóre janındaǵı toklı ótkizgishke tásir etedi. Iá tok ótip atırǵan ótkizgish dógereginde payda bolǵan magnit induktsiyası

kúsh penen tásir etedi. 9.ó hám 9.ú ni teńliklerini salıstırıp dFá = dFǵ ekenligi, yaǵnıy toktıń baǵıtı bir tárepke baǵıtlanǵan eki parallel ótkizgish bir-birine

kúsh penen tartılısıwın kóremiz.

Eger eki parallel ótkizgishlerdegi toklar baǵıtı qarama-qarsı bolsa, shep qol qádesin qollaǵan jaǵdayda, bul ótkizgishler óz-ara bir-birinen qashıwın kóriw mumkin.

2. Hárekettegi zaryadqa magnit maydanınıń tásiri. Lorents kúshi. Xoll effekti.

Magnit maydanı tek tok ótip atırǵan ótkizgishlerge ǵana tásir etip qoymastan, bálki hárakattegi zaryadlanǵan bólekshelerge hám tásir etedi. Magnit maydanında tezlikte

kúsh tásir etedi. Bul kúsh Lorents kúshi dep ataladí. Lorents kúshiniń baǵıtı shep qol qádesi

menen anıqlanadı.

Eger alaqanǵa V induktsiya sızıqları kirse, tórt achılǵan barmaq oń zaryadtıń tezlik, - vektor baǵıtına sáykes kelse, bas barmaq Lorents kúshi baǵıtın kórsetedi (q-suwret).

Háreketleniwshi zaryadlarǵa joqarıdaǵı tásirlerge tiykarlanıp tezletkichler qurılǵan. Tezletkishler járdeminde zaryadlanǵan bólekshelerge (elektronlar, protonlar, mezonlar, ionlar hám t.b.) júdá úlken energiya beriw mumkin.

Sızıqli tezletkic8. Bóleksheler joqarı kernewli generator járdeminde payda qılınǵan elektrostatik maydan járdeminde tezletiledi. Bunda Q zaryad á - ǵ potentsiallar ayırması arqalı ótkenda W=Q (á - ǵ) energiya aladı. Solay etip, bólekshe 10 MeV energiyaǵa shamalas tezletiledi.

Sızıqli rezonanslı tezletkic8. Júdá joqarı chastotalı ózgeriwshi elektr maydanında protonlar bir neshe megoelektronvoltǵa shekem, elektronlar on gigaelektronvolt energiyagǵa shekem tezletiledi.

Tsiklotron – Awır bólekshelerdi (proton, ion) tezletúchi qurılma. №urılmanıń printsipial sxeması ó-suwrette kórsetilgen.

Tsiklotronnıń tiykarǵı bólegi kúshli elektromagnit bolıp, onıń polyusları arasında duant dep atalatuǵın vakkum kamerası á hám ǵ jaylasqan. Duantlar ózgeriwshi kernewli joqarı chastotali generator polyuslarına jalǵanǵanlıǵı uchun izbe-iz birde teris, birde oń zaryadlanıp turadı.

ó–suwret

Eger zaryadlanǵan bólekshe duantlar arasındaǵı orayga kiritilse, bólekshe elektr maydanında tezleniw alıp, onıń traektoriyasi magnit maydan tásirinde iymeklenedi hám duant á ge tartıladı. Bólekshe yarim sheńberdi basıp ótip, jáne duantlar arasındaǵı sańlaqqa jetip keledi hám duant ǵ ge tartılıp tezletiledi. Usı sebepli bóleksheniń tezligi hám orbitasınıń radiusı artıp baradı. Bóleksheniń traektoriyasi spiral sıyaqlı formada jayılıp baradı hám sońında, jeterli energiyaǵa iye bolıp, arnawlı qurılma arqalı sırtqa shıǵadı. Bunday qurılmalar járdeminde protonlardı ǵ0 MeV energiyaǵa shekem tezletiw mumkin.

Bekkemlew ushın sorawlar:

1.Magnit maydanına jaylastırılǵan toklı ótkizgishlerge qanday kúsh tásir etedi ?

2.Shep qol qádesin aytíń.

3.Lorents kúshi baǵıtı qanday anıqlanadı ?

4.Xoll effektiniń mánisin túsindiriń.

137

23-tema. Elektromagnitlik induktsiya hádiysesi

Jobası:

1.Elektromagnit induktsiya hádiysesi. Lents qádesi.

2.Ózlik induktsiya hádiysesi. İnduktivlik. Óz-ara induktsiya.

3.Magnit maydan energiyası.

Tayanısh sóz hám túsinikler: Tuyıq kontur, induktsion tok, solenoid, Lents qádesi, bir tekli magnit maydanı, Faradey nızamı, Tesla, ózlik induktsiya, óz-ara induktsiya, magnit maydan energiyası.

1. Elektromagnit induktsiya hádiysesi. Lents qádesi.

Elektromagnit induktsiya hádiysesin áhqá jılı Faradey ashqan. Hádiyse sonnan ibarat, hár qanday tuyıq ótkizgish konturı menen shegaralangan bet arqalı ótip atırǵan magnit induktsiya aǵımı ózgergen waqıtta usı konturda elektr togı payda boladı. Bul tok induktsion tok dep ataladí.

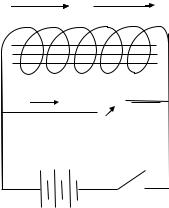
S-solenoidtı k-gilt arqalı B tok deregine jalǵasaq, A solenoidta qısqa waqıtlı tok payda boladı(ǵ-suwret).

Tájiriybelerdi analiz qılsaq, birinshi tájiriybege usı nárse xarakterli, A solenoidta tok magnit oǵan jaqınlasqanda yamasa onnan uzaqlasqan waqıtta ǵana, yaǵnıy solenoid jaqınında magnit maydan ózgergen waqıtta yamasa solenoidtıń ózi magnit maydanında kóshken waqıtta payda boladı. Magnittıń solenoidǵa salıstırǵanda háreketi yamasa solenoidtıń magnitǵa salıstırǵanda háreketi toqtawı menen solenoid jaqınındaǵı magnit maydan turaqlı bolıp qaladı hám solenoidtan tok ótpeydi. Ekinshi tájiriybegi hádiyse hám birinshidegige uqsas - bunda

ózgeriwshi magnit maydandı S solenoidta payda bolǵan yamasa joǵalıp atırǵan tok payda etedi. Eki jaǵdayda hám ótkizgish konturı jaqınındaǵı magnit maydanınıń shaması ózgeredi, demek, kontur menen shegaralanǵan bet arqalı ótiwshi magnit induktsiya aǵımı hám ózgeredi.

Peterburg universitetiniń professorı Lents induktsion toktıń baǵıti uchun tómendegi qádeni taptı: tuyıq konturda payda bolǵan tok sonday baǵıtlan boladı, bul tok konturı menen shegaralanǵan bet arqalı ótiwshi hám onıń ózin payda etiwshi magnit aǵımı induktsiyasınıń ózgeriwin kompensatsiyalawshı menshik magnit induktsiya aǵımın jaratadı.

Birinshi tájiriybe solenoidǵa magnittıń qubla polyusın jaqınlastırǵanımızda soleniodta saat strelkasına keri baǵıtlanǵan tok payda boladı(á-suwret). Bul jaǵdayda magnit payda etken induktsiya aǵımı soleniodtıń ishine qarap baǵıtlanǵan bolıp, magnit jaqınlasqan sayın artıp baradı. Solenoidtaǵı induktsion toktıń magnit maydanı sırtqı magnit maydanınıń ósiwin

138

kompensatsiyalaydı. Magnittıń qubla polyusı uzaqlastırılǵanda solenoidta saat strelkası baǵıtındaǵı tok payda boladı. Sırtqı maydanda magnit induktsiya aǵımı kemeye baslaydı. Solenoidtaǵı induktsion toktıń magnit maydanı solenoid ishine qarap baǵıtlanǵan boladı hám magnit maydanınıń kemeyiwin kompensatsiyalaydı.

Bizge belgili ózgermeli magnit induktsiya aǵımı ashıq konturda ózgermeli elektr qozǵawshı kúshti (E№K) payda etedi. E№K shaması menen magnit induktsiya aǵımınıń ózgeriw tezligi arasındaǵı baylanıstı energiyanıń saqlanıw nızamına tiykarlanıp anıqlaw mumkin.

Eger qozǵalıwshań AS bólekke iye bolǵan tuyıq konturǵa E№Ki ǵa teń bolǵan galvanik element jalǵanǵan bolsa (q-suwret), bul derektiń dt waqıt ishinde orınlaǵan jumısı

q-suwret

Eger kontur magnit maydannan sırtta turǵan bolsa, orınlanǵan jumıs Joul - Lents

Eger kontur bir tekli magnit maydanına jaylastırılsa, konturdıń AS bólegine oń tárepke qarap oǵan tik baǵıtlanǵan F kúsh tásir etedi hám onı AS halatǵa jılıstıradı. Bunda orınlanǵan mexanık jumıs

boladı.

(11.ǵ) da dF – konturdıń shtrixlangan ASA S bólegi arqalı ótip atırǵan magnit induktsiya aǵımı,

I bolsa kontur háreket etken waqıtta usı konturdan ótip atırǵan toktıń kúshi. Energiyanıń saqlanıw nızamına tiykarlanıp galvanik elementtiń orınlaǵan jumısı:

(11.ó) – ańlatpası elektromagnit induktsiya nızamın (Faradey nızamı) sıpatlaydı. Bul teńliktegi teris belginiń mánisi tómendegishe: induktsiya aǵımınıń artıwı (dF/dt>0) konturdı aylanıp

139

shıǵıwdaǵı teris baǵıt boylap tásir etiwshi E№Kti, induktsiya aǵımınıń kemeyiwi (dF/dt<0) bolsa konturndı aylanıp shıǵıwdaǵı oń baǵıt boylap tásir etiwshi E№K ti payda etedi.

İnduktsiya E№Kniń Sİ sistemasıdaǵı birligin kórip óteyik: Ei = - dF/dt = Vb/S = Tl . Mǵ/S=V

Demek, kontur beti arqalı ótiwshi magnit aǵımı á Vb/S tezlik menen ózgerse, konturda payda bolıp atırǵan E№K á V ǵa teń boladı.

2. Ózlikinduktsiya hádiysesi. İnduktivlik. Óz-ara induktsiya.

Elektromagnit induktsiya hádiysesiniń tiykarǵı nızamına tiykarlanıp, kontur beti arqalı ótip atırǵan magnit aǵımı ózgerip atırǵan barlíq jaǵdaylarda induktsiya E№Ki payda boladı.

Sonıń uchun konturdan ótip atırǵan tok kúshiniń ózgeriwi nátiyjesinde usı konturdıń ózinde induktsion E№Ki payda boladı. Bul hádiyse ózlikinduktsiya hádiysesi dep ataladí.

Máselen, konturdı (katushkanı) turaqlı tok deregine jalǵaw yamasa úziw waqıtında usı

konturdıń ózinde ózlikinduktsiya hádiysesi júzege keledi (ń-suwret).

I I

II

+-

К

ń– suwret

Gilt K jalǵanǵanda, katushkadan ótipВ atırǵan tok óziniń tolíqk mánisine birden erispeydi.

Bunnan tısqarı, katushka dógereginde payda bolatuǵın magnit aǵımı hám óziniń tolíq mánisine birden erispeydi. Lents qádesine muwapıq, payda bolıp atırǵan induktsion tok induktsiya aǵımın payda etedi, bul aǵım dáslepki magnit aǵımınıń artıwına qarsılíq etedi. Payda bolǵan induktsion tok jalǵanıp atırǵan tokka keri baǵıtlanǵan boladı (ń-suwretda tok baǵıti punktir sızıqlı strelka menen kórsetilgen). Bul tok jalǵanıw ekstra togı dep ataladí. Jalǵanıw ekstra togı kontúrdaǵı toktı kemeytiredi.

Shınjırdı úzgenimizde hám soǵan uqsas hádiyse júzege keledi. Eger konturda tok kúshi kemeyip atırǵan bolsa, konturdıń maydanı arqalı ótiwshi magnit induktsiya aǵımıda kemeyedi.

Bunday jaǵdayda tiykarǵı tok penen bir tárepke baǵıtlanǵan tok induktsiyalanadi. Bu induktsion tok uziliw ekstra togı dep ataladí. Konturdıń kúshli yamasa kúshsizraq uzinduktsiya hádiysesin kórsetiwi uzinduktsiya koeffitsenti dep atalatuǵın fizik shama menen xarakterlenedi.

Konturdan ótip atırǵan tok sebepli payda bolıp atırǵan magnit aǵımı tok kúshine proportsional, yaǵnıy:

bul jerde L – konturdıń induktivligi bolıp Sİ sistemada Genrida ólshenedi. [L] = [F/I] = Vb/A = Gn

Demek, á Gn sonday elektr shınjırınıń induktivligiki, shınjırdan á A turaqlı tok ótkende payda bolatuǵın magnit aǵım á Vb boladı.

140

Óz-ara induktsiya hádiysesi sonnan ibarat, bazıbir konturdaǵı toktıń kúshi ózgergende bul toktıń ózgeriwshi magnit maydanı qońsı konturlarda E№Kini payda etedi.

Eki (á hám ǵ) konturlardı alayıq (ú-suwret).

ә

ú-suwret

á-Konturdaǵı tok kúshi Iá bolsın. Bul tok payda qılǵan magnit induktsiya aǵımı F tok kúshi Iá ge proportsional boladı. F aǵımnıń ǵ konturdı kesib ótip atırǵan bólegin Fǵá menen belgilesek, onda

á-konturdaǵı tok kúshi Iá ózgerse, Fǵá xam ózgerip ǵ-konturda ǵ E№K payda boladı. Bul shama:

(11.h) degi Lǵá koeffitsent ǵ- kontur menen á- konturdıń óz-ara induktsiya koeffitsenti dep ataladí.

3. Magnit maydan energiyası.

Tok ótip atırǵan ótkizgishler dógereginde barlíq waqıtta magnit maydanı payda boladı hám tok ótiwi toqtawı menen magnit maydanı hám joǵaladı. Demek, tok energiyasınıń málim bir bólegi ótkizgish dógereginde magnit maydanın payda qılıwǵa sarıplanadı.

İnduktivligi L bolǵan konturdan I tok kúshi ótip atırǵan bolsın. Ótkizgish dógeregindegi aǵım tokka proportsional boladı, yaǵnıy dF=L.dI. Magnit aǵımı dF ǵa artıwı uchun dA = IdF = LIdI jumıs orınlanadı. Ol jaǵdayda F magnit aǵımın payda qılıwda orınlanǵan jumıs tómendegishe boladı:

bul jerde Sl=V solenoid kólemi. Solenoid payda etken magnit maydanı bir tekli bolıp, solenoid ortasında toplanǵanlıǵı uchun maydannıń kólemlik tıǵızlıǵı

141