
Fizika pani boyinsha lekciyalar
.pdfdesek,
(2.áq) ǵa kóre
|
2 |
|
|
|
|
á - ǵ = Ed |
(2.áń) |
||
|
1 |
|
|
|
payda boladı. Eger qo zaryadtı maydannıń qálegen tochkasına sheksizlikten alıp |
kelinse, ol |
|||
jaǵdayda orınlanǵan jumıs A = qo, |
sebebi, = 0 bunnan |
|
|
|
|
= A /qo |
|
|
(2.áó) |
formula kelip shıǵadı.
Demek, elektr maydanıń ıqtıyarıy tochkasınıń potentsialı degende usı tochkadan qo=+á zaryadtı sheksizlikke kúshiriwde orınlanǵan jumıs penen xaraterleniwshi shama túsiniledi.
Potentsialdıń ólshem birligi sıpatında elektr maydanınıń sonday tochkasınıń birligi qabıl qılınadı, bul tochkadan á Kl zaryadtı sheksizlikke kóshiriw uchun á J jumıs orınlaw kerek.
Elektr maydanınıń bunday tochkasınıń potentsialı á volt (V) dep ataladí.
(2.áó) formuladan potentsialdıń ólshem birligi
[ ] = á J/Kl = á Volt = á V
kelip shıǵadı. (2.12) formuladan kórinip tur, eger maydandı zaryadlar sisteması payda qılǵan bolsa, maydan potentsialı usı zaryadlar maydan potentsiallarınıń algebraik jıyındısına teń, yaǵnıy
n |
|
á + ǵ +.... + n = i. |
(2.áú) |
i 1 |
|
Potentsial maydannıń mine usı qásiyeti, maydannıń kúsh xarakteristikasın ańlatıwshı kernewlilikten ústin turadi, sebebi potentsial skalyar shama, kernewlilik bolsa vektor shama.
3. ELEKTROSTATIK MAYDAN KERNEWLILIGINIŃ AǴIMI. GAUSS TEOREMASI.
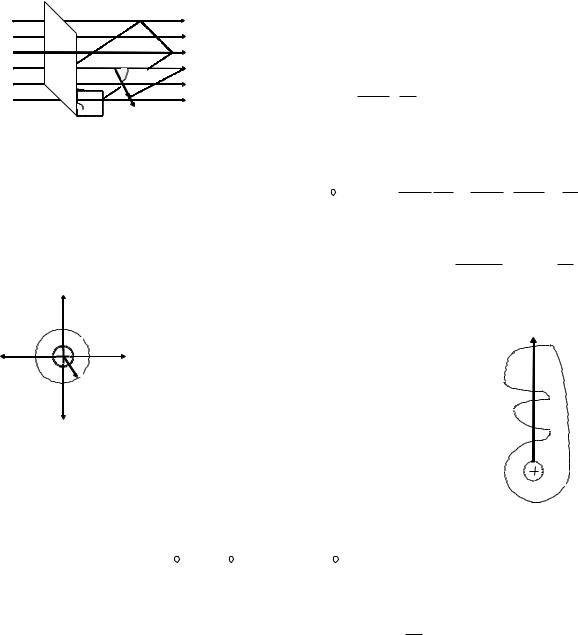
Elektrostatik maydandı maydan kúsh sızıqları (kernewlilik sızıqları) járdeminde
suwretlew mumkin. |
|
|
|
|
|
|
S - betten |
tik ótiwshi |
kúsh sızıqları sanı FE elektrostatik |
maydan kernewlilik vektorı |
|||
aǵımına teń bolıp, |
|
|
|
|
|
|
|
|
|
|
FE = En dS |
|
(3.á) |
|
|
|
|
S |
|
|
formula menen anıqlanadı, bunda En - |
|
|
normalǵa proektsiyası |
|||
E vektornıń S betke ótkerilgen n |
||||||
(3.á - suwret). |
|
|
|
|
|
|
Suwretten kórinip tur, S maydan hám onıń Sn proektsiyası arqalı birdey kernewlilik |
||||||
sızıqları ótedi, yaǵnıy |
|
|
|
|
|
|
|
|
|
|
FE = ES cos |
|
|
yamasa |
|
|
|
|
|
|
FE = En S, |
yamasa |
FE = ESn, |
(3.ǵ) |
|
||
|
|
|
|
|
|
|
bunda - E hám |
n vektorlar arasındaǵı múyes8. |
|
|
|||
102
Kulon nızamı hám elektrostatik maydanlardıń superpozitsiya printsipi ıqtıyarıy tochkalíq zaryadlar sisteması maydanın esaplaw imkaniyatın beredi. Zaryadlar uzluksiz bólistirilgen xal uchun
n
E Ei
i 1
jıyındı integralǵa almastırıladı. Biraq, bul integraldı esaplaw júdá quramalı matematik másele esaplanadı. Sonıń uchun esaplawdı ápiwayılastıratuǵın turli usullar islep shıǵılǵan. Sonday ámeliy jaqtan tiykarǵı hám ápiwayı usullardan biri elektrostatik maydanlardı esaplawǵa Gauss teoremasın qollaw.
Gauss teoreması ichinde elektr zaryadı jaylasqan tuyıq bet arqalı maydan kernewliligi
|
|
|
|
|
|
|
vektorı aǵımın esaplawǵa imkan beredi. |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
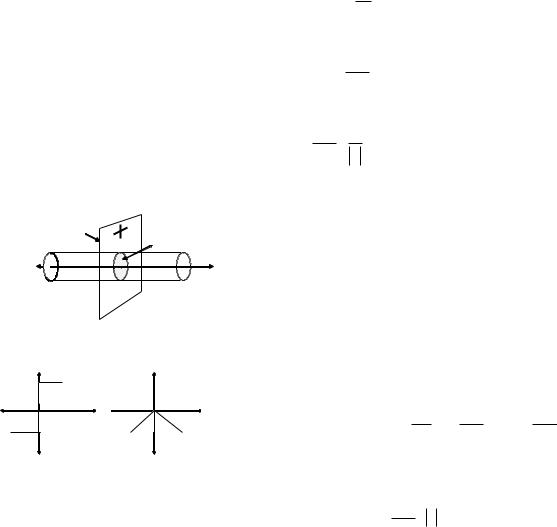
Kóz aldımızǵa keltireyik, ichi bos radiusı r bolǵan shardıń |
||||||||||||||||||||||
Sn |
|
S |
|
|
|
|
orayínda tochkalíq zaryad jaylasqan bolsın. Tochkalíq zaryadtıń r |
|||||||||||||||||||||||||
|
|
|
|
|
|
E |
aralíqdaǵı kernewliligi (3.ǵ-suwret) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
q . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
(3.q) |
|
|
|
|
|
||||||
En |
n |
|
|
|
|
|
|
|
|
|
|
|
|
40 |
|
|
r 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
3.1-сурет |
|
|
|
|
|
Usı r radiuslı sferik betten ótiwshi kernewlilik aǵımı |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
EndS |
|
q |
|
dS |
|
q |
|
4r2 |
|
|
q |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
E |
4 |
0 |
r2 |
4 |
0 |
r2 |
|
|
0 |
(3.ń) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|||
yamasa |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
ES |
q |
r 2 |
4r 2 |
|
q . |
(3.ó) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
0 |
|
|
0 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
Bu ańlatpa tek sferik |
bet |
uchun ǵana |
emes, |
|
|
|
|
|
|
|
||||||||||||||||
|
|
bálki |
|
tochkalíq |
zaryadtı |
orap |
turǵan |
|
ıqtıyarıy |
|
E |
|
|
|
|
|
||||||||||||||||
q |
E |
kórinisintegi tuyıq bet uchun hám orınlı. Eger tuyıq bet |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
r |
|
3.q-suwretdegidey |
ıqtıyarıy |
|
kórinisinde bolsa |
hám |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
kúsh |
sızıqları |
betke |
kiradi hám onnan shıǵadı. |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
Superpozitsiya printsipına tiykarlanıp, zaryadlar |
|
|
|
|
|
|
|
|||||||||||||||||||
3.2-сурет. |
|
sisteması maydanınıń kernewliligi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
Ei , |
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
||||
ol jaǵdayda qá, qǵ, ..., qn |
zaryadlar sistemasın orap turǵan ıqtıyarıy tuyıq |
|
|
|
|
|
|
|
||||||||||||||||||||||||
bet arqalı ótiwshi kernewlilik aǵımı |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.3-сурет |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
E |
|
|
EdS |
|
|
E dS |
|
E dS |
|
|
|
|
|
|
(3.ú) |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
i |
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
S |
|
|
S |
|
|
|
i |
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.ó) ǵa kóre hár bir integral qi/0 ǵa teń |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
qi |
. |
|
|
|
|
|
|
|
|
(3.w) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
i |
|
|
|
|
|
|
|
|
|
|
Bul formula vakkumdaǵı elektr maydan potentsialı uchun Gauss teoremasın sıpatlaydı.
Demek, elektr maydan kernewlilik vektorınıń ıqtıyarıy formadaǵı tuyıq bet arqalı aǵımı usı bet ishinde jaylasqan zaryadlardıń algebraik jıyındısınıń 0 ǵa bolǵan qatnasına te4.
103
Gauss teoreması járdeminde turli formadaǵı zaryadlanǵan denelerdiń maydan kernewliliklerin hám potentsialların esaplaw mumkin.
4. TURLI FORMADAǴI ZARYADLANǴAN DENELERDIŃ ELEKTR MAYDANI KERNEWLILIGI HÁM POTENTSIALIN GAUSS TEOREMASINAN PAYDALANIP ESAPLAW
a). Bir tegis zaryadlanǵan sheksiz tegisliktiń maydan kernewliligin hám potentsialın esaplaw. Sheksiz tegislik + zaryad tıǵızlıǵı menen bir tegis zaryadlanǵan bolsın, yaǵnıy
|
dq |
= sonst. |
(3.h) |
|
dS |
||||
|
|
|
Bul tegislikke perpendikulyar bolǵan(3.ń-suwret) ultanı dS ǵa teń tsilindr alayı3. Tegislik tsilindrdi teń ekige bóledı. Tsilindrdiń hár bir ultanı arqalı ótetuǵın kernewlilik aǵım EdS ǵa teń bolǵanlıǵı uchun tsilindrik bet arqalı ótken tolíq aǵım Gauss teoremasına tiykarlanıp
|
|
FE = ǵEdS, |
|
|
|
|
(3.9) |
|
|
|
|
|
|||
|
|
|
|
|
E |
1 |
qi |
dS . |
|
|
|
|
(3.10) |
||
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
(3.9) hám (3.10) ǵa kóre |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
E = |
2 |
0 |
, |
|
|
|
|
|
|
(3.áá) |
boladı. Maydanınıń ıqtıyarıy tochkasi uchun (3.áá) formulanı |
|
|
|
|
|
|
|
||||||||
|
|
|
|
E = |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 0 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kórinisinde jazıw mumkin. Formuladan kórinip turıptı, |
E tsilindrdıń uzınlıǵına baylanıslı emes, |
||||||||||||||
|
|
|
|
yaǵnıy bir tegis |
|
zaryadlanǵan |
sheksiz tegislik |
bir tekli |
|||||||
|
|
dS |
|
maydan payda etedi, biraq maydannıń bir tárepinen ekinshi |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
E |
bir tárepine ótkende E |
sekiriw menen ózgeredi. Maydan |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
kernewliligi menen maydan potentsialı arasında |
|
|
|||||||||
|
|
|
|
|
|
|
|
Ex = - (d /dx) |
|
|
|
|
|||
|
|
|
|
bolǵanlıǵı |
uchun |
x=0 |
|
hám |
x<0 |
tochkada |
maydan |
||||
|
3.4-сурет |
|
potentsialın nol dep esaplap, x0 tochkalarda zaryadlanǵan |
||||||||||||
|
|
|
|
||||||||||||
Ex |
|
|
|
sheksiz tegisliktiń maydan potentsialı (3.áá) ǵa tiykarlanıp |
|||||||||||
|
|
|
|
||||||||||||
/2 0 |
|
|
esaplanadı, yaǵnıy |
|
|
|
|
|
|
|
|
|
|||
|
|
0 |
|
|
|
|
|
|
|
|
|
||||
0 |
x |
x |
|
|
|
|
|
d |
, |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||||
|
- /2 0 |
|
|
|
|
|
|
|
x |
(3.12) |
|||||
|
|
|
|
|
|
|
|
|
dx |
2 0 |
|
2 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
a) |
|
b) |
Ulıwma jaǵdayda, x tıń ıqtıyarıy mánisi uchun maydan |
|
|||||||||||
|
3.5-сурет |
|
potentsialı |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 0 |
x |
|
|
|
|
(3.áq) |
|||
kórinisinde esaplanadı.
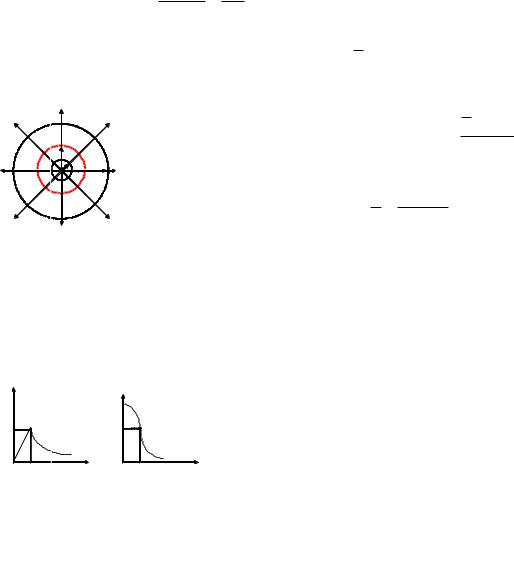
E hám lardıń x ǵa baylanıs grafikleri >0 jaǵday uchun, sáykes túrde 3.ó-suwrettiń a) hám b) bóleklerinde kórsetilgen.
104

b). Eki turli belgidegi zaryadlanǵan sheksiz parallel tegislikler arasındaǵı maydan kernewliligi hám potentsialın esaplaw.
Tegisliklar turli belgidegi + hám - zaryad tıǵızlíqları menen bir tegis zaryadlanǵan bolsın.Bul tegisliklerdiń maydan kernewliligi superpozitsiya printsipına tiykarlanıp anıqlanadı.
3.ú-suwretten kórinip tur, tegisliklerdiń shep hám oń táreplerinde maydan kúsh sızıqları qarama-
qarsı baǵıtlanǵan. Sonıń uchun bul x 0 hám x d oblastlarında juwmaqlawshı maydan
kernewliligi E =0 ǵa te4. Eki tegislik arasında (0xd) bolsa, juwmaqlawshı maydan eki tegislik maydanlarınıń jıyındısına te4.
E=E-+ E+ = |
|
|
|
|
|
|
|
. |
(3.áń) |
|
|
|
|
|
|||||
|
2 |
0 |
|
2 |
0 |
|
0 |
|
|
Eki tegislik arasındaǵı barlíq tochkalarda elektr maydan kernewliligi ǵa baylanıslı boladı. Bul aralíqta kúsh sızıqları oń zaryadlanǵan tegislikten baslanıp teris zaryadlanǵan
tegislikte tamamlanadı. |
|
|
|
|
|
|
|
Bunday maydan, yaǵnıy barlíq tochkalarda E |
niń mánisi hám baǵıti birdey bolǵan |
||
|
|
|
|
maydan, bir bir tekli maydan dep ataladı ( E =sonst).Sistemanıń potentsialı (x) |
|||
+ |
_ |
|
Ex = - d /dx |
|
|
||
|
|
teńlemeni integrallaw menen tabamız, yaǵnıy x0 aralíqta |
|
|
|
d /dx=0, = (0) = á |
|
|
|
0 x d aralíqta bolsa, |
|
E =E_-E+=0; E=E-+E+= / 0 ; |
E=E--E+=0 |
d |
|
|
0 |
||
3.6-сурет |
|
dx |
|
|
|
|
Ex |
|
|
|
|
|
desek |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
/ 0 |
|
|
|
|
|
ǵ =á 0 |
x |
||
|
|
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
0 |
d |
x |
0 |
d |
x |
Eger x=d desek, |
ǵ =á d |
boladı. |
|
|
a) |
|
|
|
|||||
|
|
|
b) |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.7-сурет |
|
|
|
x d aralíqta bolsa, d /dx=0, |
= (d) = ǵ |
||
|
|
|
|
|
|
||||
Ex hám lardıń x ǵa baylanıslı grafiklari 3.w-suwrette keltirilgen.
v). Zaryadlanǵan shar maydanı kernewliligin hám potentsialın esaplaw.
R radiusli shar bir tegis kólemlik zaryad tıǵızlıǵı menen zaryadlanǵan bolsın,
= dq/dv.
Eger r>R bolsa, ol jaǵdayda bet ishinde barlíq q zaryadlar jaylasadı. Gauss teoremasına tiykarlanıp
FE = ES = E. ńrǵ = q/0,
E |
q |
|
, bunda |
r R. |
(3.áó) |
|
|
|
|
||||
4 |
0 |
r 2 |
||||
105
Eger r=R bolsa, E |
q |
r 2 |
= |
R |
boladı. Kólemli |
zaryadlanǵanda |
shar ishinde maydan |
|||||||||
|
|
|
|
|
4 |
0 |
|
3 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
basqacha boladı, |
yaǵnıy |
r<R radiuslı cfera q= 4 |
r 3 |
zaryadtı |
|
aladi. Gauss teoremasına |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
tiykarlanıp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
r 3 |
|
|
|
|
|
|
|
|
|
|
|
|
FE = E . S = ńrǵE = q /0 = 3 |
|
0 |
|||
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
boladı, |
eger |
|
|
|
|
|
|
|
|||||
+ |
|
r |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
4 / 3R3 |
|
|
|
3.8-сурет
E |
|
|
R/2 0 |
R/3 0 |
R/3 0 |
0 |
R |
r |
|
||
|
|
3.9-сурет |
Eger r=R bolsa,
ekanligin esapqa alsaq,
|
|
|
4 / 3r3 |
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
q |
|
|
r |
|
|
r |
|
|
|
|||
E= |
|
|
4 / 3R3 |
|
|
|
|
|
(r R) (3.áú) |
|||||||||||
4r2 |
|
0 |
|
|
4 |
0 |
|
R3 |
3 |
0 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Sonday etip, bir tegis zaryadlanǵan shar sırtında maydan |
|||||||||||||||||
|
|
|
kernewliligi (3.áó) formulaǵa, ishinde bolsa (3.áú) formulaǵa |
|||||||||||||||||
|
|
|
tiykarlanıp anıqlanadı. |
|
|
|
|
|
|
|
|
|
||||||||
R |
r |
|
Shardıń potentsialı bolsa |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E= -d /dr |
|
||||
|
|
|
formuladan r R aralíq |
uchun |
|
q |
kórinisinde tabıladı. |
|||||||||||||
|
|
|
|
|||||||||||||||||
|
|
|
40 r |
|||||||||||||||||
|
|
|
(R) = |
|
|
q |
|
R2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
. |
|
|
|
|
|||||||||
|
|
|
40 R |
|
3 0 |
|
|
|
|
|||||||||||
Eger r<R bolsa, bul aralíqta potentsial
r |
|
R |
2 |
|
|
|
|
|
|
= (R)- E2 d2 |
|
|
|
|
(R2 r 2 ) |
(3.áw) |
|||
3 0 |
6 |
0 |
|||||||
R |
|
|
|
|
|||||
kórinisinde anıqlanadı.
E hám dıń r ǵa baylanıslı jaǵdayda ózgeriw grafigi 3.9-suwrettegi a) hám b) kórinisinde boladı.
BEKKEMLEW USHIN SORAWLAR:
1.Elektrostatik maydan potentsialın túsindirip beriń.
2.Elektrostatik maydan kernewlilik vektori tsirkulyatsiyasınıń mánisin aytíń.
3.Ekvipotentsial bet dep qanday betke aytıladı?
4.Elektr maydanınıń potentsialı hám kernewliligi qanday baylanısqan?
5.Kernewlilik aǵımın aytıp beriń.
106
6.Gauss teoremasın aytíń.
7.Qanday kórinisindegi zaryadlanǵan denelerdiń maydanların Gauss teoreması tiykarında esaplaw qolay?
17-tema. Elektr maydanındaǵı dielektrikler
Jobası:
1.Dielektrikler hám olardıń polyarizatsiyası.
2.Polyarizatsiya vektorı. Dielektrik sińiriwshilik hám onıń temperaturaǵa baylanıslılıǵı.
3.Baylanısqan zaryadlar.
4.Segnetoelektrikler.
Tayanısh sóz hám túsinikler: atom, molekula, elektr dipolı, dipol momenti, elastik dipol, dielektrik, polyarsız hám polyarlı molekula, orientatsion polyarizatsiya, deformatsion polyarizatsiya, ionlı polyarizatsiya, polyarizatsiya vektori, dielektrik qabıl etiwsheńlik, baylanısqan zaryadlar, izotrop dielektrik, elektr induktsiya vektorı, segnetoelektrikler, Kyuri tochkası.
|
|
|
|
|
|
|
|
|
|
1. DIELEKTRIKLER HÁM OLARDIŃ POLYARIZATSIYASI |
|||||||
|
|
|
|
|
|
Ózinen tok ótkermeytuǵın deneler dielektrikler (izolyatorlar) dep ataladı. İdeal |
|||||||||||
|
|
izolyatorlar tábiyatta joq, biraq bul deneler ótkizgishlerge qaraǵanda 10áó-10ǵ0 márte kem tok |
|||||||||||||||
|
|
ótkeredi. |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
Eger dielektrikti elektr maydanına alıp kirsek, maydan hám, dielektrik hám ózgeredi. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Bunday jaǵdaydı túsiniw |
uchun atom hám |
molekulalar quramıda oń |
||
|
|
|
|
|
|
+ |
|
|
|
F+ |
|||||||
|
|
|
|
|
|
|
|
zaryadlanǵan yadro hám |
teris zaryadlanǵan |
elektron barlıǵın itibarǵa |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
F |
|
|
|
|
|
|
|
|
|
E |
alıwımız kerek. |
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
F |
|
|
|
|
|
|
+ |
|
F+ |
|
Hár qanday molekula, juwmaqlawshı zaryadı nolge teń bolǵan |
||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
sistemadan ibarat. Buǵan elektr dipolı mısal bola aladı. |
|||||
|
|
|
|
|
4.1-расм |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Elektr maydanı atom hám molekulalardaǵı baylanısqan |
|||
|
|
zaryadlarǵa hám málim dárejede tásir kórsetedi. Bul jaǵdaydı dipol mısalında kórip óteyik. Eger |
|||||||||||||||
|
|
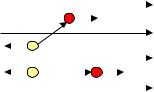
elektr maydanı bir tekli bolsa, zaryadlarǵa tásir etiwshi kúshler |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
qE |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.á) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
qE |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
san jaǵınan óz-ara teń bolıp, dipolǵa |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
M=F cos =qE cos =rEcos |
(4.ǵ) |
|
|||||
|
|
jup kúsh momenti tásir etedi. |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Eger maydan bir tekli bolmasa, M nen tısqarı dipolǵa |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
F + |
+ F - = F kúsh tásir etip, bul kúsh dipoldı kernewlilik baǵıtlanǵan tárepke qarap háreketke |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
keltiredi. Kúsh momenti |
M bolsa dipol momenti r nı sırtqı maydan kernewliligi E niń baǵıti |
||||||||||||||
boylap jaylastıradı.
107
Dielektriklerdi quraǵan molekulalardı elektr dipolına uqsatıw mumkin. Dipoldıń oń zaryadı, yadro zaryadlarınıń jıyındısına teń bolıp, ol oń zaryadlar orayínaa jaylasqan, teris zaryadı elektronlar zaryadınıń jıyındısına teń bolıp, ol teris zaryadlar orayína jaylasqan.
Eger oń zaryadlardıń orayí teris zaryadlar orayí menen ústpe-úst tússe, molekulanı polyarsız, kerisinshe bolsa, bunday molekula polyarlı molekula dep ataladí. Polyarsız molekulalarǵa Nǵ, Oǵ, Nǵ (simmetrik), polyarlı molekulalarǵa SO, NHq, HǵO, SOǵ (simmetrik bolmaǵan) lar mısal bola aladı.
Sırtqı elektr maydanı tásirinde polyarsız molekula zaryadları bir-birine salıstırǵanda jıljıydı; oń zaryadlar maydan baǵıtında, teris zaryadlar bolsa qarama-qarsı baǵıtta jıljıydı. Nátiyjede, molekula r dipol momentine iye boladı, kerisinshe r = 0 (yaǵnıy = 0). Demek,
maydan tásirida molekula polyarizatsiyalanadı. Bul polyarizatsiya elektron orbitalardıń yadroǵa salıstırǵanda jıljıwı nátiyjesinde bolıp atırǵanlıǵı uchun deformatsion polyarizatsiya (elektron polyarizatsiya) hám bunday molekula bolsa elastik dipol dep ataladı.
Polyarlı molekulalardan ibarat bolǵan dielektrikler elektr maydanı tásirine
ushıramaǵansha, olar molekulalarınıń dipol momentleri tartipsiz baǵıtlanǵan bolǵanlıǵı sebepli,
juwmaqlawshı dipol momenti vektorı ri = 0 nolge teń boladı. Sonıń uchun E = 0 bolsa, dielektrik ishinde menshik elektr maydanı bolmaydı. Bul dielektrik, elektr maydanǵa
jaylastırılsa, |
onıń molekulaları |
maydan baǵıtında |
burıladı hám |
olardıń r dipol momentleri |
|
|
|
|
|
maydan E |
boylap jaylasadı. |
r nıń mánisi E |
ǵa baylanıslı |
emes, sonıń uchun polyarlı |
molekulalardı elastik emes dipol dep júritiledi. Bunday polyarizatsiya orientatsion polyarizatsiya yamasa dipol polyarizatsiya dep ataladí hám ol temperaturaǵa keri proportsional túrde kemeyedi.
Sebebi temperatura artıwı menen dipollardıń xaotik háreketi kúsheyip, tártip buzıladı.
:shinshi gruppa dielektriklerge NaCl, KCl, Kbr, ... kristalları kiredi. Olardıń molekulaları ion dúziliske iye. Sırtqı elektr maydanı bunday dielektriklerda oń ionlardı maydan baǵıtında, teris ionlardı bolsa maydanǵa keri baǵıtta jılıstıradı. Bunday polyarizatsiya ionli polyarizatsiya dep ataladí.
2. POLYARIZATSIYA VEKTORI. DIELEKTRIK QABIL ETIWSHEŃLIK HÁM ONIŃ
TEMPERATURAǴA BAYLANISLILIǴI
Dielektriktiń polyarizatsiya dárejesin xarakterlew uchun polyarizatsiya vektorı dep atalatuǵın shama qollanıladı.
Polyarizatsiya vektorı P degende dielektriklertiń birlik kólemindegi barlíq dipollar elektr momentleriniń vektor jıyındısı túsiniledi.
Bir tekli bolmaǵan dielektriklerde, onıń qálegen birar tochkasındaǵı polyarizatsiya vektorı haqqında pikir júritiw mumkin. Bunıń uchun usı tochka dógereginde elementar V kólem ajratamız. Bul kólem ishindegi barlíq dipollar momentleriniń vektor jıyındısınınıń usı V kólemge qatnası,
|
|
|
|
|
pi |
|
|
P im |
i |
(4.q) |
|
V |
|||
V 0 |
|
dielektriktiń polyarizatsiya vektorın sıpatlaydı.
108
|
|
|
|
|
Tájiriybelerdiń kórsetiwinshe, izotrop dielektriklerde polyarizatsiya |
vektorı |
P menen |
||
|
|
|
|
|
maydan kernewliligi E (eger |
E júdá úlken bolmasa) arasındaǵı tómendegishe baylanıs bar. |
|||
|
|
|
|
|
|
P = 0 |
E |
|
(4.ń) |
- dielektriktiń tábiyatini sıpatlaydıgan oń ólshemsiz ( > 0) |
shama bolıp, |
ol dielektrik qabıl |
||
|
|
|
|
|
etiwsheńlik dep ataladí. Ol |
E ge baylanıslı emes. Polyarsız molekulalardan |
quralǵan |
||
dielektriklertiń temperaturaǵa baylanıslı emes, polyarlı |
dielektriklertiki bolsa temperaturaǵa |
||||||||
á/T tárizde baylanısqan boladı. Kópchilik dielektriklertiń |
sı birden oncha úlken emes, biraq |
||||||||
spirt uchun = ǵó hám |
suv uchun bolsa = h0 ge te4. |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Polyarsız |
dielektrikler |
uchun (4.ń) |
formula P =n0 P e=n0 0 E kórinisinde jazıladı, |
onı (4.ń) |
|||||
formulaǵa teńlep |
= n0 |
ekanligin |
kóremiz, bunda = |
ńRq |
– |
atomnıń |
|||
polyarzatsiyalanıwshılıǵı dep ataladí. Polyarlı |
dielektriklerde bolsa |
(4.q) |
formula tómendegi |
||||||
kórinisinde jazıladı. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P = n0 < P e>, |
|
|
|
|
|
|
|
|
|
bunda |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
< P e> = ( pe2 /qkT) E |
|
|
|
|
||
bunı (4.ń) ge teńlestirsek |
|
|
|
|
|
|
|
||
|
|
|
|
|
= n0 |
pe2 /q0kT |
|
(4.ó) |
|
ekenligin kóremiz. Bul ańlatpa DepayLanjeven formulası dep ataladí.
3. BAYLANISQAN ZARYADLAR
Kóz |
aldımızǵa |
keltireyik, |
dielektrik |
kernewliligi |
E |
bolǵan |
elektr |
maydanına |
|||||||
jaylastırılǵan bolsın (suwret-4.q). Maydan tásirinde dielektrik polyarizatsiyalanadı. Yaǵnıy onıń |
|||||||||||||||
molekulalarındaǵı oń hám teris zaryadlar, sáykes túrde maydan hám oǵan keri baǵıtlarda jıljıydı. |
|||||||||||||||
Bunda qońsı dipollardıń qarama-qarsı zaryadları birin-biri neytralaydı. Biraq, dielektriktiń shep |
|||||||||||||||
a |
|
b |
|
|
|
hám oń tárepindegi betlerinde jaylasqan teris hám oń zaryadlar |
|||||||||
|
|
|
|
|
|
óz-ara neytrallaspaydı. Yaǵnıy, onıń shep betinde teris, ońında |
|||||||||
+ |
+ |
S |
|
bolsa |
oń |
zaryadlar |
toplanadı. |
Bul |
zaryadlar |
dielektrik |
|||||
|
+ |
|
+ |
|
Е |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
molekulalari menen baylanısqan bolǵani uchun kóshe almaydı. |
|||||||||||||
|
+ |
|
+ |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
4.3-сурет. |
Sonıń |
uchun olardı |
baylanısqan |
zaryadlar |
hám |
dielektriktiń |
|||||
a’ |
|
b’ |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
polyarizatsiyası sebepli payda bolǵanlıǵı uchun bolsa |
||||||||||||
|
|
|
|
|
|
||||||||||
polyarizatsiyalanǵan bet zaryadları dep ataladí. Bet zaryadları payda etken ishki maydan sırtqı |
|||||||||||||||
maydanǵa keri baǵıtlanǵanligi sebepli, dielektrik ishinde sırtqı maydan hálsireydi, |
|
||||||||||||||
Bet zaryadların q menen, olardıń bet tıǵızlıǵın bolsa menen belgileymiz. Ol jaǵdayda, |
|||||||||||||||
4.q-suwrettegi dielektrikti iyini maydanı S, zaryadlari q = .S teń bolǵan dipol dep qaraw |
|||||||||||||||
mumkin. Bul dipoldıń elektr momenti R = S . boladı. Polyarizatsiya vektorınıń mánisi |
|||||||||||||||
|
|
|
|
|
|
|
P = R/ V = = S . / V = = q / S |
(4.ú) |
|||||||
|
|
|
|
|
|
|
|
|
q = R S |
|
|
|
|
(4.w) |
|
Demek, q , R menen S tiń kóbeymesine te4. |
|
|
|
|
|
|
|||||||||
Endi bir tekli bolmaǵan dielektrik berilgen bolsın: |
|
|
|
|
|
|
|
||||||||
109
|
|
|
Bir tekli bolmaǵan dielektrik E |
elektr maydanına kiritilse, E |
niń baǵıtında dielektrik |
molekulalarınıń kontsentratsiyası artıp baradı, yaǵnıy Rǵ>Rá, buǵan tiykarlanıp q ǵ > qá boladı. Dielektrik kóleminde payda bolıwshı bul artıqcha zaryadlardıń muǵdarı
qkólem = qá - qǵ = RáS - RǵS = (Rá - Rǵ) S =- (Rǵ - Rá) S |
(4.h) |
|
|
aa vv tuyıq bet |
|
Gauss teoremasına tiykarlanıp ekinshi tárepdan P polyarizatsiya vektorınıń |
||
arqalı aǵımı, yaǵnıy |
|
|
FR=RǵS-RáS= =(Rǵ -Rá)S |
(4.9) |
|
(4.h) hám (4.9) lardı salıstırıw nátiyjesinde tómendegini payda qılamız: |
|
|
FR = - qkólem |
(4.10) |
|
bunda qkólem = qi baylanısqan zaryadlar jıyındısına te4. |
|
|
Ol jaǵdayda |
|
|
|
|
|
|
|
a |
|
|
b |
|
|
|
|
|
FR = |
RndS = - qi |
(4.áá) |
||
|
|
|
|
|
|
+ |
|
|
|
+ |
S |
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
Demek, dielektrik ishinde alınǵan ıqtıyarıy tuyıq bet arqalı |
||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
+ |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
Е |
|
|
|
|||||
|
|
|
|
|
|
+ |
|
|
|
+ |
|
|
|
|
P nıń aǵımı usı bet penen shegaralangan kólemdegi baylanısqan |
|||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
zaryadlardıń algebraik |
jıyındısınıń keri |
belgi menen alınǵan |
|||
|
|
|
|
|
+ |
|
|
|
+ |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
a’ |
|
|
b’ |
|
|
q2 |
|
mánisine te4. |
|
|
||||
|
q1 |
|
|
|
|
4.4-расм. |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. SEGNETOELEKTRIKLER |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dielektriklerde dipollar tártipsiz jaylasqanligi uchun E = 0 da, |
P = 0 boladı. Biraq, |
|||||||||||||
kópshilik dielektrikler uchun ornılı bolǵan bul jaǵday segnetoelektrikler dep atalıwshı bir gruppa zatlar uchun orınlı bolmaydı.
Bul gruppanıń birinshi wákilleri segnet duzı(NaKCńHńOú . |
ńHǵO |
hám TiOq) titanat |
bariylar. |
|
|
1. Segnetoelektriklerde dielektrik sińdiriwsheńlik basqa zatlarǵa salıstırǵanda júdá úlken, |
||
yaǵnıy >>á boladı. Máselen: segnet duzı uchun = 10000 , bariy titanatı uchun = w000. |
||
|
|
|
2. Segnetoelektriklerdiń si E ǵa baylanıslı. Sonıń uchun |
P nıń |
E ga baylanıslılıǵı |
sızıqli emes.
3.Segnetoelektriklerdiń polyarizatsiya P vektorı onıń dáslepki jaǵdayına hám baylanıslı.
Máselen, 4.9-suwrette E nıń á mánisine P nıń q mánisi sáykes keledi. Segnetoelektriklerdiń bu qásiyetleri olarda domenlar dep atalıwshı spontan polyarizatsiya aralíqları bar ekenligi menen túsindiriledi.
P
4.9-suwret
Рs |
А |
|
|
|
|
|
|
|
|
Eger segnetoelektrik ózgeriwshi |
E |
maydanǵa jaylastırılsa, |
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ondaǵı P |
nıń ózgeriwi gisterezis |
sızıǵı (4.9-suwret) dep |
|
-Es |
K |
К’ |
|
|
atalatuǵın |
tuyıq iymek sızıqtan |
ibarat boladı. Rk – qaldıq |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
E |
|
|
|
|
|
|
|
Es |
polyarizatsiya, Ek - koertsitiv kús8. Bunday qásiyet hár bir |
|||
|
|
|
|
|
|
|
|
|
|
|
|
4.9 - сурет |
|
segnetoelektrik uchun tiyisli bolǵan temperaturaga shekem |
|||
|
D’ |
|
|
|
||||
A’ |
-Рs |
|
|
|
yamasa temperaturalar aralıǵında |
boladı. Bul temperaturalar |
||
|
|
|
|
|
Kyuri tochkaları dep ataladí. Máselen: segnet duzı uchun ǵóh |
|||
110

K hám ǵ9h K (-áó0S hám +ǵǵ,ó0S) lar aralıǵında segnetoelektriklik qásiyetleri bayqaladı.
Segnetoelektriklerdi hám bazı simmetriya orayína iye bolmaǵan kristallardı mexanık tásir sebepli deformatsiyalasaq, olar polyarizatsiyalanadı. Payda bolǵan zaryad muǵdarı tásir kúshine tuwrı proportsional. Bul hádiyse tuwrıpezoelektrik effekt dep ataladí.
Házirgi waqıtda segnetoelektrik qásiyetlerine iye bolǵan júdá kóp dielektrik zatlar anıqlangan. Olardan kondensatorlarda, ultrases generatorlarında keń paydalanıladı.
BEKKEMLEW USHIN SORAWLAR:
1.Polyarizatsiyalanǵan hám polyarizatsiyalanbaǵan dielektriklerdiń parqın aytíń.
2.Polyarizatsiya vektorın aytıp beriń.
3.Dielektrikler uchun Gauss teoremasın aytíń.
4.Gisterezis sızıǵın túsindiriń.
18-tema. Elektr sıyımlılıǵı. Kondensatorlar
Jobası:
1.İzolyatsilanǵan ótkizgishtiń elektr sıyımlılıǵı.
2.Kondensatorlar
3.Zaryadlanǵan kondensator energiyası.
tayanısh sózler hám túsinikler : elektr sıyımlılıǵı, Farada, kandensator, kondensatorni jalǵaw, izolyatsilanǵan ótkizgish, elektrostatik maydan energiyası, energiyanıń kólemiy tıǵızlıǵı.
1. İzolyatsilanǵan ótkizgishtiń elektr sıyımlılıǵı.
Dógeregindegi ótkizgishlerdiń elektr maydanı tásir qıla almaytuǵın aralíqda jaylasqan ótkizgish izolyatsilanǵan ótkizgish dep ataladí. Bunday ótkizgishtiń potentsialı zaryad muǵdarına tuwrı proportsional boladı
Cq ,
bundagi S ti ótkizgishtiń elektr sıyımlılıǵı yamasa sıyımlılíq dep ataladí hám onnan:
S |
q |
. |
(5.q) Ótkizgishtiń elektr sıyımlılıǵı san jaǵınan |
|
|||
|
|
||
onıń potentsialın bir birlikke arttırıw uchun kerek bolǵan zaryad muǵdarına te4. Sıyımlılíq ótkizgishtiń geometrik ólshemlarine hám onı orap turǵan ortalíqtıń dielektrik sińiriwshiligine baylanıslı boladı. Turli formadaǵı ótkizgishler sıyımlılıǵıni (5.q) járdeminde anıqlaw mumkin.
Bizge belgili, zaryadlanǵan R radiuslı shardıń betindegi potentsialı
111
