
Дисциплина: Физика
Тема: 060 Механические колебания и волны
V061 – П Механические колебания

S061 – П Механические колебания (незатухающие, затухающие, вынужденные 30 заданий)
*Уд1+ (ВО1) Полная механическая энергия пружинного маятника увеличилась в 2 раза. При этом амплитуда колебаний … раз(а).
увеличилась в 2
Увеличилась в 2
уменьшилась в 2
Уменьшилась в 2

:2
Вторым продуктом ядерной реакции Be+He=C+ .. НЕЙТРОН
*Уд1+ (ВО1) Материальная точка совершает гармонические колебания по закону x xm sin 0t . График, на котором изображена зависимость проекции ускорения ax этой точки от времени t –

1 ЕСЛИ ПО КОСИНУСУ, ТО 4ый график
2
3
4
:1
Абсолютно черное тело имеет температуру 2900, в результате остывания тела длина волны, на которую приходится максимум спектральной плотности энергетической светимости, изменилась на 9 мкм , тело охладилось до температуры ОТВЕТ – 290 К
3. *Уд1+ (ВО1) Материальная точка совершает колебания по закону x xm sin 0t . График, на котором изображена зависимость кинетической энергии материальной точки от времени –

1
2
3
4
:2
4. *Уд1+ (ВО1) Материальная точка совершает колебания по закону x xm sin 0t . График, на котором изображена зависимость потенциальной энергии материальной точки от времени –
1
2
3
4) 4
:4
*Уд1+ (ВО1) На рисунке представлены
графикигармоническихколебаний
материальных точек одинаковой массы,
А1=2А2. Соотношение амплитудных значений ускорений колеблющихся точек следующее
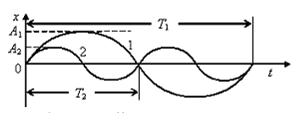
am1 = am2
a m1 < am2
a m1 > am2
Однозначного ответа нет
:2
На рисунке представлены графики гармонических колебаний зарядов в двух колебательных контурах…Если индуктивности одинаковы, то отношением емкостей = 4
Ответ -4
Если при неизменном омическом сопротивлении в колебательном контуре увеличить в 2 раза индуктивность катушки, то коэффициент затухания
уменьшится в 4 раза
*Уд1+ (ВО1) На рисунке представлены графики гармонических колебаний материальных точек одинаковой массы, А1=2А2. Соотношение амплитудных значений скоростей колеблющихся точек следующее
V m1 = Vm2
V m1 < Vm2
V m1 > Vm2
Однозначного ответа нет
:1
*Уд1+ (ВО1) Даны уравнения гармонических колебаний четырёх пружинных маятников с одинаковыми коэффициентами упругости k. Маятник, имеющий наибольшую массу – … кг.
|
|
|
|
|
1) |
x 2 sin 4t |
|
|
|
|
|
|||
|
|
4 |
|
|
5 cos5 t
2
x 6cos2t
|
|
|
|
|
4) |
x 4 sin |
t |
|
|
|
|
|
3 |
|
:4 |
|
|
|
|
*Уд1+ (ВО1) Даны уравнения гармонических колебаний четырёх пружинных маятников с одинаковыми коэффициентами упругости k. Маятник, имеющий наименьшую массу – … кг.
|
|
|
|
|
|
||||
1) |
x 2 sin 4t |
|
|
|
|
|
|||
4 |
|
|
|||||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
||||
|
|
|
|
|
|||||
2) |
x 5 cos5t |
|
|
|
|
|
|||
|
|
2 |
|
|
|||||
x 6 cos2t
|
|
|
|
|
||
4) |
x 4 sin |
t |
|
|
|
|
|
|
|||||
|
|
|
3 |
|
||
:2 |
|
|
|
|
|
|
*Уд1+ (ВО1) Даны уравнения гармонических колебаний четырёх пружинных маятников с одинаковыми массами. Маятник, имеющий наибольший коэффициент упругости k – … Н/м.
|
|
|
|
|
|
|
|
|
||||
1) |
x 2 sin 4t |
|
|
|
|
|
|
|||||
4 |
|
|||||||||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||
2) |
x 5 cos |
5t |
|
|
|
|
|
|
|
|||
|
|
|
|
|
2 |
|
|
|||||
3) |
x 6 cos2t |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||||
4) |
x 4 sin |
t |
|
|
|
|
|
|
|
|||
3 |
|
|
|
|||||||||
|
|
|
|
|
|
|
||||||
:2 |
|
|
|
|
|
|
|
|
|
|
|
|
*Уд1+ (ВО1) Даны уравнения гармонических колебаний четырёх пружинных маятников с одинаковыми массами. Маятник, имеющий наименьший коэффициент упругости k – … Н/м.
|
|
|
|
|
1) |
x 2 sin 4t |
|
|
|
|
|
|||
|
|
4 |
|
|
5 cos5 t
2
x 6 cos2t
|
|
|
|
|
4) |
x 4 sin |
t |
|
|
|
|
|
3 |
|
:4
*Уд1+ (ВО1) Даны уравнения гармонических колебаний материальной точки массы m . Коэффициент упругости k наибольший в случае
х = 3 sin (2πt + π) м
х = 3 cos (4πt + 2 ) м
x = 5 cos (15πt – 2 ) м
x = 5 sin (5πt) м

:3
[Уд1] (ВО1) На рис.1 изображена
зависимость проекции скорости материальной точки, совершающей гармонические колебания, от времени. На рис.2 график зависимости от времени проекции ускорения этой точки изображен под номером
1) 1
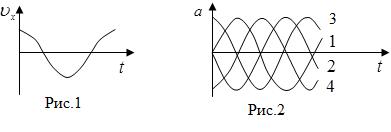
2
3
4
:2
[Уд1] (ВО1) На рис.1 изображена
зависимостьпроекциискорости
материальной точки, совершающей гармонические колебания, от времени. На рис.2 график зависимости от времени
смещения от положения равновесия этой точки изображен под номером
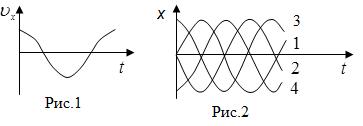
1
2
3
4
:1
*Уд1+ (ВО1) Материальная точка массой m = 0,1 кг колеблется так, что проекция ах ускорения зависит от времени в соответствии с уравнением
ах = 10 sin 102 t , м/с2. Проекция силы на ось ОХ, действующей на материальную точку в момент времени t = 5 c равна … Н.


6
0,25
0,5
0,83
1,0
: 2
*Уд1+ (ВО1) Если в колебательной системе изменяющаяся физическая
величина описывается законом x xm et cos(t 0 ) , то частота затухающих колебаний связана с собственной частотой соотношением
0
0
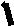
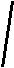 0222
0222
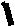 022
022


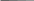
:4
*Уд1+ (ВО1) Уравнение затухающих колебаний материальной точки имеет
вид x A et cos(t |
0 |
) , где = 6 рад/с, = 8 с-1. Логарифмический |
|
0 |
|
|
декремент затухания колебаний равен
83,7
8,37
0,63
62,8
:2
*Уд1+ (ВО1) Уравнение затухающих колебаний материальной точки имеет
вид x A et cos(t |
0 |
) , где = 6 рад/с, логарифмический декремент |
|
0 |
|
|
затухания = 8,37 . Коэффициент затухания колебаний равен … с-1.
1) 8,0
2) 1,3
3) 0,6
4) 3,0
:1
*Уд1+ (ВО1) Уравнение затухающих колебаний материальной точки имеет вид x 0,02e4t cos(t 3) ,м. Если логарифмический декремент затухания колебаний λ = 0,1, то период T затухающих колебаний равен … мс.
1) 20
2) 25
40
75
:2
*Уд1+ (ВО1) Уравнение затухающих колебаний материальной точки имеет вид x 0, 01e 3t cos( t 4) ,м. Если логарифмический декремент затухания колебаний λ = 0,02, то частота ω затухающих колебаний равна … рад/с.
50
100
200
300
:4
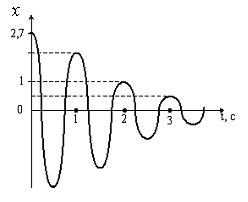
*Уд1+ (ВО1) На рисунке изображен график затухающих колебаний, где х - колеблющаяся
величина, описываемая уравнением х(t) = A0e-βt sin (ωt + φ). Коэффициент затухания
равен
0,5
1
2
2,7
:1
*Уд1+ (ВО1) Приведены графики механических колебаний. Два графика соответствуют зависимости смещения х, два других – зависимости
кинетической Wk и полной энергии W системы от времени. Обозначения вертикальных осей не указаны.
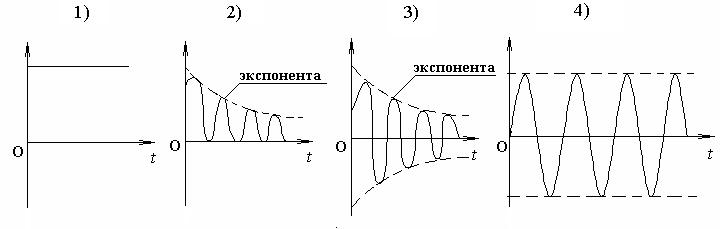
Зависимости кинетической энергии системы от времени в неконсервативной системе соответствует график
1
2
3
4
:2
Приведены графики зависимости кинетической Wк и полной механической W энергии от времени t при различных видах механических колебаний.
Зависимость полной энергии W от времени в неконсервативной системе описывается графиком 1
*Уд1+ (ВО1) Приведены графики механических колебаний. Два графика соответствуют зависимости смещения х, два других – зависимости
кинетической Wk и полной энергии W системы от времени. Обозначения вертикальных осей не указаны.
Зависимости полной энергии W системы от времени в консервативной системе соответствует график
1
2
3
4
:1
*Уд1+ (ВО1) Приведены графики механических колебаний. Два графика
соответствуют зависимости смещения х, два других – зависимости кинетической Wk и полной энергии W системы от времени. Обозначения вертикальных осей не указаны.
Зависимости смещения х от времени в консервативной системе соответствует график
1) 1
2
3
4
:4
*Уд1+ (ВО1) Приведены графики механических колебаний. Два графика
соответствуют зависимости смещения х, два других – зависимости кинетической Wk и полной энергии W системы от времени. Обозначения вертикальных осей не указаны.
Зависимости смещения х от времени в неконсервативной системе соответствует график
1
2
3
4
:3
*Уд1+ (ВО1) Приведены графики зависимости кинетической Wк и полной механической W энергии от времени t при различных видах механических колебаний. Обозначения осей ординат не указаны.
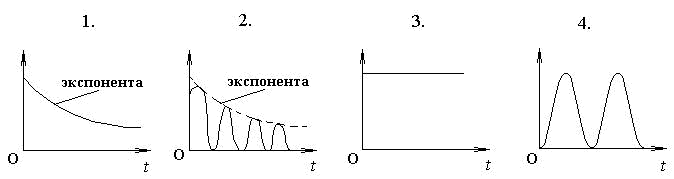
Зависимость полной энергии W от времени описывается … графиками.
1 и 2
2 и 4
3 и 1
4 и 3
:3
26. |
|
*Уд1+ |
|
(ВО1) |
Уравнение |
движения пружинного маятника |
|
|||||
|
d 2 x |
|
|
r |
|
dx |
|
k |
x 0 |
является |
дифференциальным уравнением … |
|
|
dt 2 |
|
m |
dt |
m |
|
||||||
|
|
|
|
|
|
|
|
|
||||
колебаний.
свободных незатухающих
затухающих
вынужденных
апериодических
:2
*Уд1+ (ВО1) Уравнение движения пружинного маятника является дифференциальным уравнением … колебаний.
свободных незатухающих
затухающих
вынужденных
d 2 x k x 0 dt 2 m

апериодических
:1
28. |
|
|
*Уд1+ |
(ВО1) |
Уравнение движения пружинного маятника |
|
|||||||||||||||||||
|
d |
2 |
x |
|
r dx |
k |
F |
|
является дифференциальным уравнением … |
|
|||||||||||||||
|
|
|
0 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
cos t |
|
|||||||||||||
|
dt 2 |
m |
dt |
m |
m |
|
|
||||||||||||||||||
колебаний.
свободных незатухающих
затухающих
вынужденных
апериодических
:3
29. |
*Уд1+ |
(ВО1) |
Решение |
дифференциального |
уравнения |
|
|||||||||
|
d 2 x |
2 |
dx |
2 |
x 0 |
движения пружинного маятника ищется в виде |
|
||||||||
|
|
|
|
||||||||||||
|
dt2 |
|
dt |
0 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||||
зависимости
х = Acos (ω0t +o)
х = Ao e-t cos (ωt +o)
3) x = 2A cos |
|
t cosωt |
|
2 |
|
||
|
|
|
х = Ao e-2t cos (ω0t +o)
:2
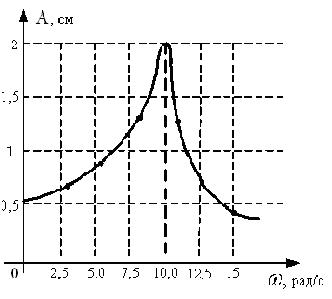
*Уд1+ (ВО1) На рисунке представлена зависимость амплитуды колебаний груза на
пружине с жесткостью k = 10 Н/м от частоты
внешней силы. Максимальная энергия в этой системе равна … Дж.
0,002
0,004
20
40
:1
C061 – П Механические колебания (сложение колебаний) – 16 заданий
*Уд1+ (ВОМ) На рисунке под номерами 1, 2 изображены траектории результирующего движения при сложении двух взаимно перпендикулярных гармонических колебаний, а под номерами 3, 4 – векторные диаграммы
сложения |
гармонических колебаний одного |
направления |
и |
одинаковой |
||||
|
|
|
|
|
|
|||
частоты ( À1, À2 |
- векторы амплитуд складываемых колебаний, |
Ар - вектор |
||||||
амплитуды |
|
результирующего колебания). |
Амплитуды |
складываемых |
||||
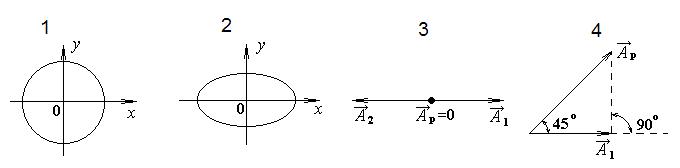
колебаний равны для случаев, приведенных под номерами
:1,3,4
*Уд1+ (ВО1)Точка участвует одновременно в двух взаимно
перпендикулярных колебаниях, выражаемых уравнениями x = 3cost и
= -6cost. Траекторией результирующего движения точки является
прямая линия
парабола
окружность
эллипс
:1
[Уд1] (ВО1) Складываются два гармонических колебания, происходящих в одном направлении.
1) |
x 5, 2 cos( t |
|
) , м |
и |
|
||||
|
|
||||||||
|
1 |
2 |
|
|
|
|
|
||
|
|
|
|
|
|
||||
|
|
|
|
|
|
||||
2) |
х1 |
5cos1,20 t |
|
|
|
, м |
|
||
2 |
|
||||||||
|
|
|
|
|
|
||||
3) |
x1 5cos( t 0,50 ) , м и |
|
||||
|
|
|
|
|
||
4) |
х1 |
5cos1,20 t |
|
|
, м |
|
|
|
|
||||
|
|
|
|
2 |
|
|
x2 5, 4 cos( t 2) , м.
|
|
|
|
|
||
и |
х1 |
5cos1,22 t |
|
|
, м. |
|
|
|
|
||||
|
|
|
|
2 |
|
|
x2 5cos( t 0,52 ) , м.
|
|
|
|
||
и х1 |
5cos1,50 t |
|
|
, м. |
|
|
|
|
|||
|
|
|
2 |
|
|
Результирующее движение называется биением в (во) … случае.
1
2
3
4
:2
*Уд1+ (ВО1) Складываются два гармонических колебания, происходящих в
|
|
|
|
|
|
|
3cos t см. Амплитуда |
|
|||||
одном направлении: x |
|
4cos |
t |
|
см и |
x |
2 |
|
|||||
|
|
|
|||||||||||
|
2 |
|
|
2 |
|
|
|
||||||
результирующего движения равна … см.
7
5
3,5
1
:2
*Уд1+ (ВО1) Результат сложения двух гармонических колебаний одного направления с одинаковыми амплитудами и близкими частотами описывает уравнение
х = Acos (ω0t +o)
A2 = A12 +A22 + 2A1A2 cos
3) x = 2A cos |
|
t cosωt |
|
2 |
|
||
|
|
|
x 2 y 2 2xy cos sin2
A2 B 2 AB

:3
*Уд1+ (ВО1) Уравнение траектории при сложении двух гармонических колебаний взаимно перпендикулярных направлений с отличающимися амплитудами и одинаковыми частотами –
х = Acos (ω0t +o)
A2 = A12 +A22 + 2A1A2 cos
3) |
x = 2A cos |
|
t cosωt |
|
|
||||||||||||
2 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2 |
2 |
|
|
2xy |
|
|
|
|||||||||
4) |
|
x |
|
y |
|
|
cos sin2 |
|
|
||||||||
|
2 |
2 |
|
|
|||||||||||||
|
|
A |
|
B |
|
AB |
|
|
|||||||||
:4 |
|
|
|
|
|
|
|
|
|
|
|
||||||
*Уд1+ (ВО1)Точка М одновременно совершает колебания по
гармоническому закону вдоль осей координат ОХ и ОУ с одинаковыми
амплитудами, разность фаз равна 2 . При соотношении частот 1:1 траектория точки имеет вид, соответствующий схеме под номером
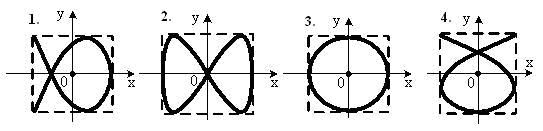
1
2
3
4
:3
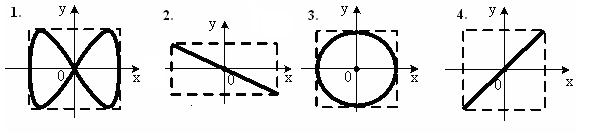
*Уд1+ (ВО1) Колебания точки М происходят вдоль осей Ох и Оу по закону
синуса с различными амплитудами, но одинаковыми частотами. При разности фаз π траектория точки имеет вид, соответствующий схеме под номером
1
2
3
4
:2
*Уд1+ (ВО1) Колебания точки М происходят вдоль осей Ох и Оу по закону синуса с одинаковыми амплитудами, и одинаковыми частотами. При
разности фаз 0 траектория точки имеет вид, соответствующий схеме под номером
1
2
3
4
:4
*Уд1+ (ВО1) Колебания точки М происходят вдоль осей Ох и Оу по закону синуса с одинаковыми амплитудами, но разными частотами. При разности фаз π/2 траектория точки имеет вид, соответствующий схеме под номером
1
2
3
4
:1
*Уд1+ (ВО1) Точка М одновременно колеблется по гармоническому закону вдоль оcей координат ОХ и ОУ с одинаковыми амплитудами, разность
фаз равна 2 . При соотношении частот 3:2 траектория точки имеет вид на схеме, обозначенной номером
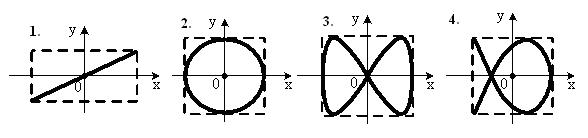
1
2
3
4
:4
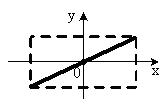
*Уд1+ (ВО1) При сложении двух взаимно-перпендикулярных колебаний одинаковой частоты
траектория результирующего движения материальной точки представлена на рисунке. Тогда разность фаз складываемых колебаний равна
π
0
3π
π/2
:2
[Уд1] (ВО1) Два гармонических колебания происходят с одинаковыми периодами в одном направлении с амплитудами А1=4 см и А2=3 см.
Амплитуда их результирующего колебания Ар=7 см. Разность фаз складываемых колебаний равна
∆φ = 0
∆φ = 4
∆φ = 2
∆φ = π
:1
[Уд1] (ВО1) Два гармонических колебания происходят с одинаковыми периодами в одном направлении с амплитудами А1 = 4 см и А2 = 3 см. Амплитуда их результирующего колебания Ар = 5 см. Разность фаз складываемых колебаний равна
1) ∆φ = 0
∆φ = 4
∆φ = 2
∆φ = π

:3
[Уд1] (ВО1) Два гармонических колебания происходят с одинаковыми периодами в одном направлении с амплитудами А1 = 4 см и А2 = 3 см. Амплитуда их результирующего колебания Ар = 1 см. Разность фаз складываемых колебаний равна
1) ∆φ = 0
2) ∆φ =
4
3) ∆φ =
2
4) ∆φ = π
:4
[Уд1] (ВО1) Два гармонических колебания происходят с одинаковыми периодами в одном направлении с амплитудами А1 = 4 см и А2 = 3 см.
Разность фаз складываемых колебаний равна ∆φ = |
|
. Амплитуда их |
|
2 |
|
||
результирующего колебания составляет … см. |
|
|
|
|
|
|
7
5
1
12
:2
Дисциплина: Физика
Тема: 060 Механические колебания и волны
V064 – П Волновое движение
S064 – П Волновое движение - 10 заданий
1. *Уд1+ (ВО1) Решением волнового уравнения |
2 |
|
1 |
|
2 |
является |
|
|
x |
2 |
u 2 |
|
t 2 |
|
|||
|
|
|
|
|
||||
уравнение плоской монохроматической волны , которая распространяется вдоль направления оси Ох. Это уравнение представлено формулой
m cos(t 0 )
m sin( kx 0 )
m sin( t 0 )
m cos(t kx 0 )


:4
2. *Уд1+ (ВО1) Уравнение плоской синусоидальной волны, распространяющейся вдоль оси Ох со скоростью v = 500 м/с, имеет вид
= 0,01 sin (ωt – 2х). Циклическая частота ω равна … рад·с-1. 1) 1000
2) 159
3) 0,02
4) 0,001 :1
*Уд1+ (ВО1) Уравнение плоской монохроматической волны , которая распространяется вдоль положительного направления оси Ох представлено формулой
m cos(t 0 )
m sin( kx 0 )
m sin( t kx 0 )
m cos(t kx 0 )
:4
*Уд1+ (ВО1) Уравнение сферической монохроматической волны представлено формулой
m cos(t 0 )
m sin( kr 0 )
3) |
|
m |
cos(t kr |
|
) |
|
|
|
0 |
|
|||||
|
|
r |
|
|
|||
m cos(t kr 0 )

:3
*Уд1+ (ВО1) Уравнение стоячей волны представлено формулой
m cos(t 0 )
2m cost cos(kr)
3) |
|
m |
cos(t kr |
|
) |
|
|
|
0 |
|
|||||
|
|
r |
|
|
|||
m cos(t kr 0 )
:2
*Уд1+ (ВО1) При интерференции двух волн результирующая волна характеризуется изменением
частоты волны
длины волны
распределения энергии в пространстве
периода колебаний
:3
*Уд1+ (ВО1) Источник колебаний, находится в упругой среде, и точки этой
среды находятся на расстоянии l 2 м от источника. Частота колебаний

5 Гц, фазовая скорость волны 40 м/с. Разность фаз равна … рад.
1) 2π
2) 0,5π
3) 0,25π
4) 0,33π
:2
*Уд1+ (ВО1) Если разность фаз колебаний источника волн в упругой среде равна = 0,5π рад, и точки этой среды находятся на расстоянии l 2 м от источника. Частота колебаний составляет 5 Гц, тогда фазовая скорость волны равна … м/с.
20
30
40
50
:3
*Уд1+ (О) Точки пространства, в которых амплитуда колебаний стоячей волны, равна нулю, называются … стоячей волны.
Узлы, узлами
*Уд1+ (ВО1) В стоячей волне расстояния между двумя соседними пучностями равно
/2
3/2
2
:2
C064 – П Волновое движение (графики) – 4 задания
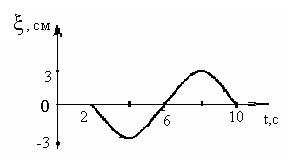
*Уд1+ (ВО1) В упругой среде в положительном направлении оси 0x распространяется плоская волна. На рисунке приведен график зависимости смещения ξ частицы среды от времени t в произвольной точке оси 0х. Циклическая частота волны … рад/c.
2π
0,8π
π/4
π/3
:3
*Уд1+ (ВО1) В упругой среде в положительном направлении оси 0x распространяется плоская волна. На рисунке приведен график зависимости
смещения ξ частицы среды от времени t в произвольной точке оси 0х. Если длина волны равна 40 м, то скорость распространения составляет … м/c.
2
5
3) 8
10
:2
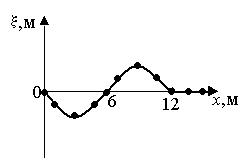
*Уд1+ (ВО1) На рисунке приведена моментальная «фотография» модели плоской поперечной гармонической волны в момент времени t = 6 с. Источник колебаний находится в точке с координатой х = 0. В начальный момент времени (t = 0) все частицы среды находились в покое. Фазовая скорость волны равна … м/c.
12
6
4
2
:4
*Уд1+ (ВО1) На рисунке приведена моментальная «фотография» модели плоской поперечной гармонической волны в момент времени t = 6 с. Источник колебаний находится в точке с координатой х = 0. В начальный момент времени (t = 0) все частицы среды находились в покое. Циклическая частота волны равна … рад/c.
2π
0,8π
π/4
π/3
:4
Дисциплина: Физика
Тема: 240 Электромагнитная индукция
