01_Абрамкин_ЭМЭиС_2019

Выбор типа регулятора и расчет его параметров производят с целью получения технически оптимального переходного процесса. Технически оптимальным считается переходный процесс, когда установившееся значение регулируемой координаты достигается за минимально возможное время при перерегулировании y < 4–10 %. Эти требования обеспечивают компромисс между быстрым процессом с большим перерегулированием и медленным процессом с меньшим перерегулированием.

Приведем принципы коррекции динамических показателей СУ с подчиненным регулированием.

Пусть ОУ описывается передаточной функцией

где Tr >> Ts – большие и малые постоянные времени элементов ОУ. Предположим, что последовательно в контур ОУ включен регулятор с пе-

редаточной функцией

При введении регулятора из передаточной функции исключаются u инерционных звеньев и n частных коэффициентов, поэтому все показатели регулирования в (3.5) определяются только постоянными времени. Для повышения точности регулирования в передаточную функцию введено интегрирующее звено с постоянной времени T0. Соответственно контур регулирования приобретает астатизм первого порядка.

50

В (3.5) нескомпенсированными остались v малых постоянных времени. Их компенсация нецелесообразна в связи со сложностью практической реализации. Отметим, что влияние элементов с малой инерционностью на качество переходного процесса невелико. В связи с этим совокупность v звеньев можно заменить одним апериодическим звеном с суммарной постоянной времени Tμ, т. е. принять

представим в виде

Отсюда передаточная функция замкнутого контура регулирования

где a = T0 / Tµ – соотношение постоянных времени контура регулирования. При a < 4 переходный процесс – колебательный. Собственная частота

Таким образом, значение a определяет характер и длительность переходного процесса в контуре. Пользуясь соотношением постоянных (3.6) можно преобразовать:

51

При скачкообразном входном воздействии переходный процесс имеет колебательный характер (рис. 3.8). Длительность процесса t1 = 4,7Tμ, перерегу-

контур I на рис. 3.7 настроен в соответствии с (3.7), т. е.

В знаменателе (3.8) без большой погрешности можно пренебречь слагае-

вания II будет

В соответствии с принципами коррекции приводим (3.9) к виду

Значит, регулятор контура II должен иметь передаточную функцию

Таким образом, для компенсации большой постоянной времени T2 в контуре с апериодическим звеном необходим ПИ-регулятор. Числитель передаточной функции ПИ-регулятора (3.10) имеет форсирующее звено (T2s + 1). Значит, инерционность объекта компенсируется форсированием входного сигнала. Однако такой регулятор при скачкообразном воздействии формирует импульсный сигнал

52

с бесконечно большой амплитудой. Практически это нереализуемо, поэтому полная компенсация регуляторами этого типа невозможна.

Отметим, что сигнал на выходе ПИ-регулятора остается неизменным только в том случае, если входной сигнал равен нулю. Входным сигналом ПИрегулятора является сигнал рассогласования (ошибки). Таким образом, установившийся режим в контуре с ПИ-регулятором наступает только при устранении ошибки регулирования. Такое регулирование называется астатическим.

В результате коррекции передаточные функции разомкнутого и замкнутого контура II приобретают вид:

Объект контура III СУ на рис. 3.7 предположительно также является апериодическим звеном первого порядка

Wо3(s) k3 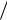(T3s 1) .

Включив в этот контур ПИ-регулятор

получим передаточную функцию замкнутого внешнего контура в виде

Алгоритм настройки на n контуров даст передаточную функцию n-го замкнутого контура вида

При настройке всех контуров на ТО a = 2

53

Отметим, что вывод (3.12) осуществлялся в предположении, что все нескомпенсированные постоянные времени относятся к внутреннему контуру регулирования.

Таким образом, переходные процессы в контурах системы подчиненного регулирования, настроенных на ТО, носят одинаковый характер. Быстродействие же по мере удаления от внутреннего контура уменьшается. Это вызвано возрастанием нескомпенсированной постоянной T n

Для более высокой точности регулирования применяют настройку на симметричный оптимум (СО). Желаемая передаточная функция разомкнутого контура при такой настройке имеет вид

Выражение (3.13) можно распространить на n-й контур при подстановке в него T n = 2n–1T 1.

Название настройки на СО происходит от вида логарифмической ампли- тудно-частотной характеристики (ЛАЧХ). В ней количество сопрягаемых частот и наклон асимптот симметричны по отношению к частоте среза 1/(2Tμ) (рис. 3.9).

L(ω)

Рис. 3.9. Сравнение ЛАЧХ системы подчиненного регулирования

при настройках на ТО и СО

После замыкания контура обратной связью передаточная функция при настройке на СО имеет вид

54

При скачкообразном управляющем воздействии значение перерегулирования возрастает по сравнению с настройкой на ТО более чем в 10 раз и достигает 47 %. Также увеличивается и длительность переходного процесса с t1 = 4,7Tμ до t1 = 6,2Tμ. Перерегулирование уменьшается до 6,2 % при установке на входе регулятора фильтра (инерционного звена)

однако при этом время регулирования возрастает до t1 = 14,4Tμ. Современные преобразователи СУ ЭП имеют встроенные ПИД-регуля-

торы. Их работа обеспечивается вводом в память коэффициентов пропорциональной, интегральной и дифференциальной составляющих (kП; kИ; kД). Если коэффициент какой-либо составляющей не введен, то это соответствует нулевому значению. Для вычисления коэффициентов передаточную функцию регулятора нужно представить суммой. Например, для регулятора (3.11) коэффициенты примут вид:

на рис. 3.6, работающей в зоне II (область, где оба контура регулирования замкнуты). Структурная схема этой СУ показана на рис. 3.10, а. На схеме приняты следующие обозначения: gω, gM – заданные значения угловой скорости и момента (тока); Wgω, WgM – передаточные функции регуляторов угловой скорости и момента (тока); k – передаточный коэффициент преобразователя; h – жесткость естественной механической характеристики; Tµ, Tя, Tэм – постоянные времени суммарная, якоря и электромеханическая; M – момент ЭД; Mc – момент нагрузки; ω – угловая скорость.

55

Пренебрежем влиянием внутренней обратной связи двигателя по ЭДС. Тогда контур регулирования момента (тока) представим в виде двух апериодических звеньев первого порядка с постоянными времени якоря Tя = Lя / rя и эквивалентной малой постоянной Tμ << Tя. Она учитывает запаздывание импульсного источника питания и фильтров.

Рис. 3.10. Структурная схема системы управления ЭП:

а– с замкнутыми контурами регулирования скорости и момента;

б– с замкнутым контуром скорости

Исходная передаточная функция контура регулирования момента

В результате коррекции получаем желаемую передаточную функцию вида

Значит, передаточная функция регулятора для компенсации большой постоянной времени Tя имеет вид

Таким образом, передаточная функция разомкнутого контура регулирования момента

а после замыкания:

56

Полагая в (3.14) s = 0, для статического режима получим M = gM = const. В этом случае механические характеристики ЭД абсолютно мягкие. При изменении сигнала задания M = gM = const они смещаются параллельно (рис. 3.11, а). Выбором соотношения постоянных времени aM определяются динамические свойства контура момента (тока). Обычно он настраивается на ТО (aM = 2).

Рис. 3.11. Механические характеристики ЭД:

а– в замкнутой системе регулирования момента;

б– в замкнутой системе регулирования угловой скорости

Пренебрегая в (3.14) слагаемым второго порядка получим упрощенную передаточную функцию замкнутого контура регулирования момента

Структурная схема для настройки регулятора тока показана на рис. 3.10, б. Здесь нескорректированный контур скорости имеет передаточную функцию

где Tэм >> 2T – электромеханическая постоянная времени.

57

Выбором П-регулятора с передаточной функцией

Окончательно для замкнутого контура скорости получим

или, выбирая настройку контура скорости на ТО и полагая aM = aω = 2,

Структурная схема на рис. 3.10, б позволяет получить уравнение динамической механической характеристики при настройке на ТО в виде

Отсюда уравнение статической механической характеристики (s = 0)

Из (3.16) следует, что в замкнутой системе регулирования угловой скорости, настроенной на ТО, жесткость механической характеристики зависит от соотношения нескомпенсированной и электромеханической постоянных времени. При Tэм > 4Tμ жесткость характеристики выше, чем в разомкнутой системе h. Если Tэм = 4Tμ, то статическая механическая характеристика замкнутой системы такая же, как разомкнутой. В случае Tэм < 4Tμ механическая характеристика ЭД в замкнутой системе будет мягче, чем в разомкнутой (рис. 3.11, б).

Если для коррекции статической ошибки регулирования скорости вращения вместо П-регулятора применить ПИ-регулятор, то ее можно исключить и получить абсолютно жесткую механическую характеристику. Действительно, подставив передаточную функцию ПИ-регулятора в (3.16) получим

s 0

Wg (4T s 1) 4T s .

58

Тогда (3.16) при постоянном сигнале задания gω0 = const будет иметь вид константы gω0 = ω = const.

Ограничить вращающий момент ЭД позволяет введение в контур регулирования скорости после регулятора нелинейного звена типа насыщения

ным значением максимального момента Mmax:

(g 0 ) hTэм gMп Mmax .

4T

Когда ЭД достигает скорости вращения ωп, нелинейный элемент насыщается и обратная связь по скорости размыкается. При этом в системе регулирования работает только контур момента (тока). Механическая характеристика такой ситуации показана на рис. 3.11, б.

3.2. Системы управления скоростью асинхронных двигателей с фазным ротором

Способы регулирования скорости вращения короткозамкнутых АД рассмотрены в [11]–[13]. В основном они реализуются в разомкнутых СУ. Замкнутые СУ применяются при векторном управлении. Такое управление характеризуется сложной математической обработкой тока статора. Он раскладывается на составляющие, одна из которых пропорциональна потокосцеплению ротора, а вторая – электромагнитному моменту. Это позволяет использовать для управления АД те же принципы построения СУ, что и для ДПТ НВ.

ВАД с фазным ротором могут быть реализованы функции наблюдения

ирегулирования координат, которые формируют электромагнитный момент. Например, ток ротора, сила которого при постоянном потокосцеплении определяет момент на валу АД. Регулирование тока можно реализовать параметрическим способом. При этом изменяется добавочное сопротивление в цепи ротора или регулируется напряжение питания АД. Эти способы характеризуются низкими энергетическими показателями и простотой реализации. Их применяют в ЭП малой мощности. В ЭП средней и большой мощности для

59