
Лабораторные / 9091_Боброва Лаб4
.docxМИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра АПУ
отчЕт
по лабораторной работе №4
«Дискретные системы»
по дисциплине «Математические основы теории систем»
Выполнила: Боброва Н.Ю.
Факультет: ФКТИ
Группа № 9091
Преподаватель: Каплун Д.И.
Санкт-Петербург
2022
ЛАБОРАТОРНАЯ РАБОТА №4.
ДИСКРЕТНЫЕ СИСТЕМЫ
Цель работы: знакомство с дискретными системами и операцией дискретной свертки; расчет импульсной и частотных характеристик; изучение визуальных средств проектирования цифровых фильтров.
Основные теоретические сведения:
В общем случае дискретный фильтр суммирует (с весовыми коэффициентами) некоторое количество входных отчетов (включая последний) и некоторое количество предыдущих выходных отсчетов. Выделяют фильтры с конечной импульсной характеристикой (КИХ-фильтры) и с бесконечной импульсной характеристикой (БИХ-фильтры). Главным отличием БИХ-фильтров является наличие обратной связи и потенциальная неустойчивость.
КИХ-фильтр обладает рядом полезных свойств, из-за которых он иногда более предпочтителен в использовании, чем БИХ-фильтр.
Вот некоторые из них: КИХ-фильтры устойчивы; КИХ-фильтры при реализации не требуют наличия обратной связи; фаза КИХ-фильтров может быть сделана линейной.
Ход работы.
Для заданных уравнений рассчитаем реакции КИХ и БИХ фильтров 3-го порядка.
%kih3
b= [0.2 0.3 0.5 0.7];
a= [1];
n=0:0.25:64;
x=0.1*sin (0.7*n);
y=filter (b,a,x);
stem (n,x)
hold on
stem (n,y, '*')
%bih3
b= [1 1 1 1];
a= [1 0.3 -0.25 -0.4];
n=0:0.25:64;
x=0.1*sin(0.7*n);
y=filter(b,a,x);
figure
stem(n,x)
hold on
stem(n,y, '*')
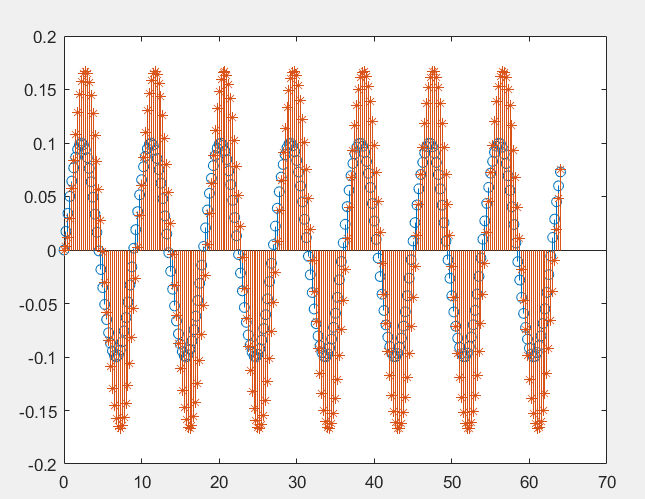
Рисунок 1 – Реакция КИХ-фильтра

Рисунок 2 – Реакция БИХ-фильтра
Двумя способами вычислим импульсную характеристику БИХ-фильтра, при помощи функции зададим также число отсчетов и частоту дискретизации:
%imp har
%1
N=80;
for n=1:N
X(n)=0;
end
X(40)=0.1*sin(0.7*40);
Y=zeros(1,N);
Ma=4;
for n=Ma:N
Y(n)=abs(X(n)+X(n-1)+X(n-2)+X(n-3)+0.3*Y(n-1)-0.25*Y(n-2)-0.4*Y(n-3));
end
figure
stem(X)
hold on
stem(Y)
%2
[h,t]=impz(b,a,80,5000);
figure
stem(t,h)
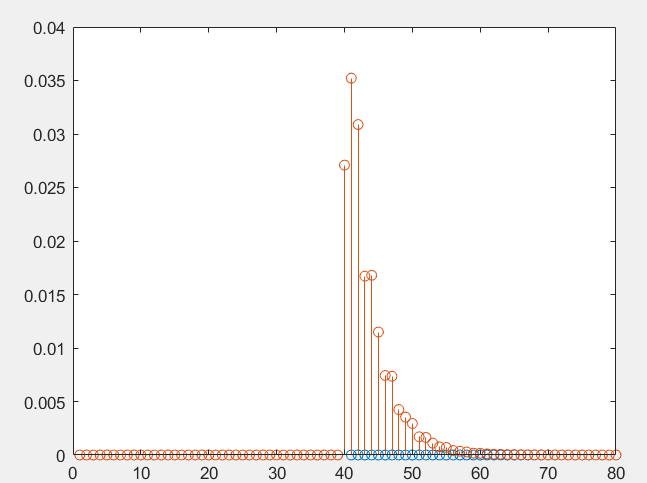
Рисунок 3 – Импульсная характеристика БИХ-фильтра
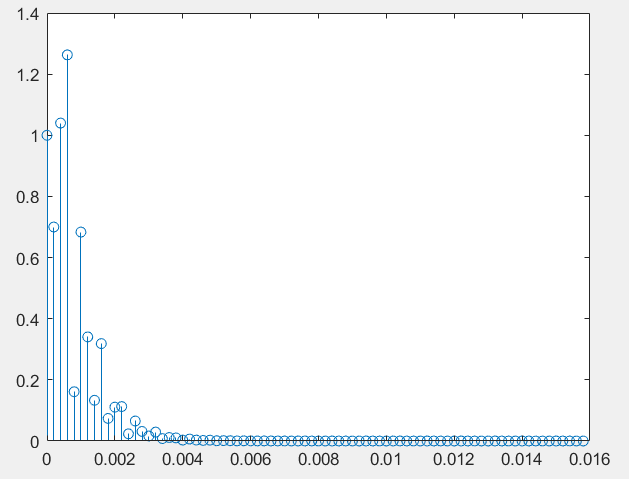
Рисунок 4 – Импульсная характеристика БИХ-фильтра
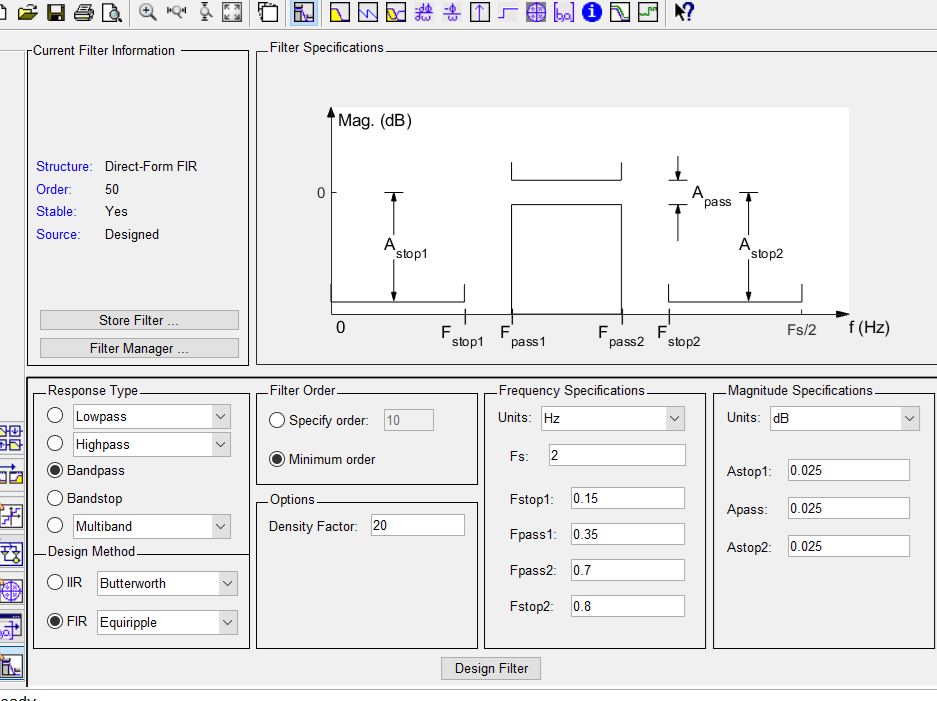
При помощи FilterDesign сгенерируем фильтр с заданными параметрами (полоса пропускания 0,35–0,7; – полоса задерживания 0–0,15 0,8–1; – неравномерности по 0,025 в ПП и ПЗ) и получим его ИХ, АЧХ и ФЧХ:
Генерация фильтра:
АЧХ:
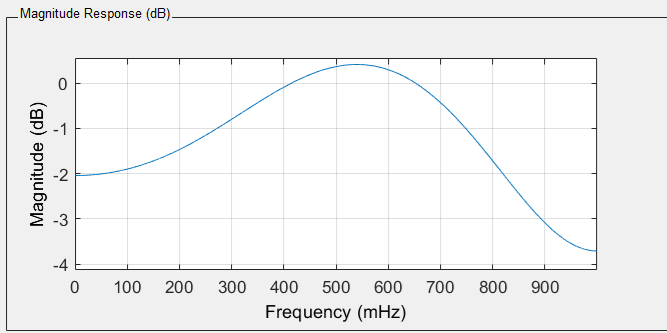
ФЧХ:
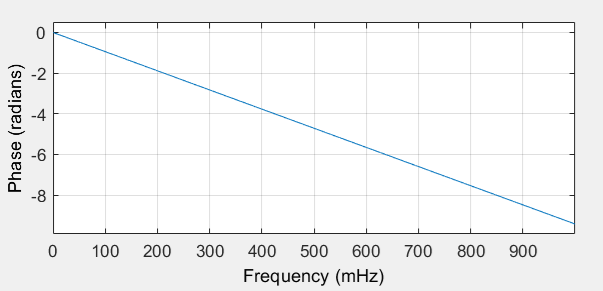
Импульсная характеристика:

По заданным коэффициентам фильтра получим его ИХ, АЧХ, ФЧХ:
%filter
k=[0 0,026477 0 0 0 -0,044116 0 0 0 0,093436 0 0 0 -0,31394 0 0,5 0 -0,31394 0 0 0 0,093436 0 0 0 -0,044116 0 0 0 0,026477 0];
K=abs(fft(k,1000));
Kk=angle(fft(k,1000));
figure
subplot(3,1,1)
stem(k)
subplot(3,1,2)
plot(K)
subplot(3,1,3)
plot(Kk)

Данный фильтр, как и фильтр из предыдущего пункта, является полосовым пропускающим КИХ-фильтром.
Вывод:
При выполнении данной лабораторной работы были несколькими способами реализованы КИХ и БИХ-фильтры, получена их реакция, построены АЧХ, ФЧХ, ИХ.
Код программы:
close all
clear all
%kih3
b= [0.2 0.3 0.5 0.7];
a= [1];
n=0:0.25:64;
x=0.1*sin (0.7*n);
y=filter (b,a,x);
stem (n,x)
hold on
stem (n,y, '*')
%bih3
b= [1 1 1 1];
a= [1 0.3 -0.25 -0.4];
n=0:0.25:64;
x=0.1*sin(0.7*n);
y=filter(b,a,x);
figure
stem(n,x)
hold on
stem(n,y, '*')
%imp har
%1
N=80;
for n=1:N
X(n)=0;
end
X(40)=0.1*sin(0.7*40);
Y=zeros(1,N);
Ma=4;
for n=Ma:N
Y(n)=abs(X(n)+X(n-1)+X(n-2)+X(n-3)+0.3*Y(n-1)-0.25*Y(n-2)-0.4*Y(n-3));
end
figure
stem(X)
hold on
stem(Y)
%2
[h,t]=impz(b,a,80,5000);
figure
stem(t,h)
%filter
k=[0 0,026477 0 0 0 -0,044116 0 0 0 0,093436 0 0 0 -0,31394 0 0,5 0 -0,31394 0 0 0 0,093436 0 0 0 -0,044116 0 0 0 0,026477 0];
K=abs(fft(k,1000));
Kk=angle(fft(k,1000));
figure
subplot(3,1,1)
stem(k)
subplot(3,1,2)
plot(K)
subplot(3,1,3)
plot(Kk)
