Лабораторные / 9091_Боброва Лаб3

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра АПУ

отчЕт

по лабораторной работе №3

«Спектр. Ряд Фурье»

по дисциплине «Математические основы теории систем»

Выполнила: Боброва Н.Ю.

Факультет: ФКТИ

Группа № 9091

Преподаватель: Каплун Д.И.

Санкт-Петербург

2022

ЛАБОРАТОРНАЯ РАБОТА №3.

СПЕКТР. РЯД ФУРЬЕ

Цель работы: знакомство со спектральным представлением периодических и случайных процессов; изучение взаимосвязи преобразований сигналов во временной и частотной областях; оценка дефектов дискретного преобразования Фурье и методы их подавления.

Основные теоретические сведения:

Чтобы построить спектр с помощью ДПФ (БПФ), надо определить следующие параметры:

• количество спектральных составляющих;

• шаг между соседними частотами – разрешение по частоте Δƒ;

• частоту дискретизации;

• минимальную (нижнюю) частоту спектра;

• верхнюю частоту;

• временной интервал анализа Т.

На самом деле эти параметры жестко связаны друг с другом, и для однозначного построения спектра достаточно задать всего две величины.

Как правило, анализ начинается с выбора временной базы анализа Т и частоты дискретизации 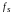. При этом оказываются определенными и количество отсчетов сигнала 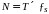, и минимальная частота спектра: 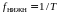. А поскольку количество спектральных коэффициентов равно количеству отсчетов сигнала 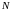, оказываются определенными и верхняя частота преобразования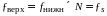 , и шаг между соседними частотами .

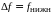Ход работы.

1. Создадим 2 сигнала, заданные функциями косинуса с разной частотой. Путем сложения и перемножения этих сигналов, получим сигналы х3 и х4. Построим модуль спектра всех сигналов.

f1=100;

Fd1=300;

f2=150;

Fd2=500;

T1=1/Fd1;

T2=1/Fd2;

tmax=0.05;

t=(0:0.0001:tmax);

x1=cos(2*pi*f1*t);

x2=4*cos(2*pi*f2*t);

x3=x1+x2;

x4=x1.*x2;

plot(t,x1)

hold on

plot(t,x2);

%spektri

figure

subplot(4,1,1)

plot(abs(fft(x1)));

subplot(4,1,2)

plot(abs(fft(x2)));

subplot(4,1,3)

plot(abs(fft(x3)));

subplot(4,1,4)

plot(abs(fft(x4)));

На рисунке представлен модуль спектра каждого сигнала.

Рисунок 1 – Модуль спектра

Если колебание периодическое, то есть характеризуется интервалом времени Т (периодом) таким, что s(t+T)=s(t), его можно представить суммой гармонических колебаний с определенными амплитудами и начальными фазами. Частоты гармоник кратны частоте следования колебаний равной 1/Т. Таким образом, спектр периодического колебания является дискретным или линейчатым. При линейном сложении сигналов их спектры складываются. При умножении сигналов в спектре полученного сигнала появляется разность и сумма спектров.

2. Рассмотрим δ-импульс на временном интервале отсчетов N=2⁷.

%imp

t=0:1/127:1;

n=length(t);

imp =[1; zeros(1,1);zeros(n-1+1,1)];

figure

subplot(3,2,1)

plot(imp)

subplot(3,2,3)

plot(abs(fft(imp)))

subplot(3,2,5)

plot(angle(fft(imp)))

%sdvig imp

imp1 = [zeros(10,1);1 ; zeros(n-10+1, 1)];

subplot(3,2,2)

plot(imp1)

subplot(3,2,4)

plot(abs(fft(imp1)))

subplot(3,2,6)

plot(angle(fft(imp1)))

%izm shirini imp

t=0:1/127:1;

n=length(t);

figure

for i = 0:128

imp0 = [zeros(i,1);1 ; zeros(n-i-1, 1)];

%plot(abs(fft(imp0)))

End

Рассмотрим модуль и фазу спектра и сдвинутого спектра (сдвиг равен 10).

Рисунок 2 – Спектр δ-импульса

АЧС не изменяется, а ФЧС изменяется пропорционально -artcg(n), где n – сдвиг дельта импульса на n отсчетов.

В цикле for последовательно увеличиваем ширину импульса, наблюдая соответствующие изменения спектра: АЧС не изменяется.

3. Создадим периодический прямоугольный сигнал со скважностью 2 (меандр) и количеством периодов, кратным двум. Построим его спектр.

%meandr

signal = zeros(1,128);

for i = 1:2:16

signal(i*8:i*8+8) = 1;

end;

figure

subplot(3,1,1)

plot(t, signal);

subplot(3,1,2)

plot(abs(fft(signal)));

subplot(3,1,3)

plot(angle(fft(signal)));

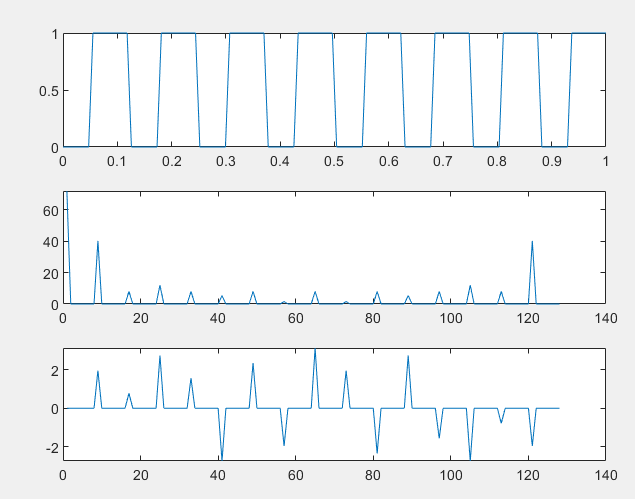
Рисунок 3 – Меандр и его спектр

4. Определим форму и ширину частотной характеристики двух соседних каналов анализатора Фурье. Это можно сделать в цикле for, изменяя частоту анализируемого сигнала с достаточно малым шагом (0.1 – 0.2) и выделяя из спектра только отчет, принадлежащий выбранному каналу.

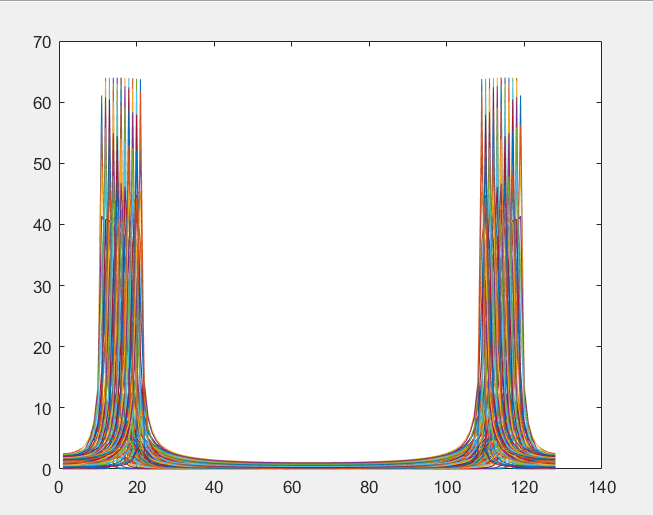
Рисунок 5 – Изменения спектра

Вывод:

При выполнении данной лабораторной работы были рассмотрены спектры сигналов синусоидальной формы, рассмотрены случаи спектров сигналов при суммировании и перемножении сигналов с одной частотой. Рассмотрен спектр δ-импульса (со смещением и без), исследовано изменение ФЧС ( фазо-частотного спектра) и АЧС (амплитудно-частотного спектра) при увеличении его ширины. Рассмотрен спектр меандра.

Код программы:

close all

clear all

f1=100;

Fd1=300;

f2=150;

Fd2=500;

T1=1/Fd1;

T2=1/Fd2;

tmax=0.05;

t=(0:0.0001:tmax);

x1=cos(2*pi*f1*t);

x2=4*cos(2*pi*f2*t);

x3=x1+x2;

x4=x1.*x2;

plot(t,x1)

hold on

plot(t,x2);

%spektri

figure

subplot(4,1,1)

plot(abs(fft(x1)));

subplot(4,1,2)

plot(abs(fft(x2)));

subplot(4,1,3)

plot(abs(fft(x3)));

subplot(4,1,4)

plot(abs(fft(x4)));

%imp

t=0:1/127:1;

n=length(t);

imp =[1; zeros(1,1);zeros(n-1+1,1)];

figure

subplot(3,2,1)

plot(imp)

subplot(3,2,3)

plot(abs(fft(imp)))

subplot(3,2,5)

plot(angle(fft(imp)))

%sdvig imp

imp1 = [zeros(10,1);1 ; zeros(n-10+1, 1)];

subplot(3,2,2)

plot(imp1)

subplot(3,2,4)

plot(abs(fft(imp1)))

subplot(3,2,6)

plot(angle(fft(imp1)))

%izm shirini imp

t=0:1/127:1;

n=length(t);

figure

for i = 0:128

imp0 = [zeros(i,1);1 ; zeros(n-i-1, 1)];

%plot(abs(fft(imp0)))

end

%meandr

signal = zeros(1,128);

for i = 1:2:16

signal(i*8:i*8+8) = 1;

end;

figure

subplot(3,1,1)

plot(t, signal);

subplot(3,1,2)

plot(abs(fft(signal)));

subplot(3,1,3)

plot(angle(fft(signal)));

%2kanala

figure

for i = 1:100

f = 10 + 0.1*i;

S = cos(2*pi*f*t);

plot((abs(fft(S))));

hold on;

end;