
Лабораторные / 9091_Боброва Лаб2
.docxМИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра АПУ
отчЕт
по лабораторной работе №2
«КОРРЕЛЯЦИОННЫЙ МЕТОД ИЗМЕРЕНИЯ ЗАДЕРЖКИ СИГНАЛА»
по дисциплине «Математические основы теории систем»
Выполнила: Боброва Н.Ю.
Факультет: ФКТИ
Группа № 9091
Преподаватель: Каплун Д.И.
Санкт-Петербург
2022
ЛАБОРАТОРНАЯ РАБОТА №2.
КОРРЕЛЯЦИОННЫЙ МЕТОД ИЗМЕРЕНИЯ ЗАДЕРЖКИ СИГНАЛА
Цель работы: анализ возможностей корреляционных методов выделения сигнала из шума и измерения его параметров.
Основные теоретические сведения:
Корреляция и ее частный случай для центрированных сигналов (ковариация) – это мера схожести двух сигналов.
Скалярное произведение сигнала с собственной копией, скользящей по аргументу называют автокорреляционной функцией – АКФ. Автокорреляция позволяет оценить среднестатистическую зависимость текущих отсчетов сигнала от своих предыдущих и последующих значений (так называемый радиус корреляции значений сигнала), а также выявить в сигнале наличие периодически повторяющихся элементов.
КФ, вычисленная по центрированному значению сигнала, представляет собой ковариационную функцию сигнала.
Ход работы.
Рассмотрим задачу измерения высоты полета самолета. Проще всего послать вертикально вниз короткий радиоимпульс и измерить при помощи корреляционной функции задержку импульса, отраженного от земли. Команда conv(X,Y) для выполнения свертки (скольжения по τ) предварительно увеличит вдвое длину вектора Y.
X=zeros (1,1000);
Y=zeros (1,1000);
X(1:100)=5; % излучаемый импульс с амплитудой 5 и длительностью 100 отсчетов
Y(301:400)=1; % принятый импульс запоздал на 300 отсчетов
C=conv(X,Y);
plot(C);
На рисунке представлен график корреляционной функции.
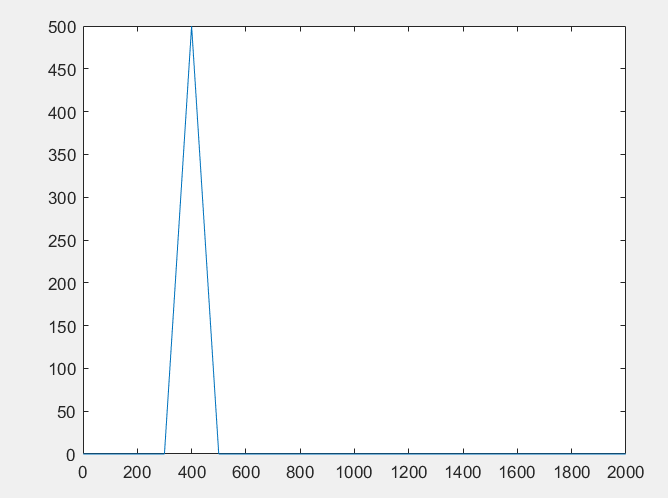
Рисунок 1 – График корреляционной функции
Измерение
высоты полета при помощи одиночного
прямоугольного импульса обладает двумя
серьезными недостатками: малой
помехозащищенностью (можно поймать
чужой импульс) и пологой формой
 ,
не позволяющей
гарантировать точность определения
задержки при наличии шума.
,
не позволяющей
гарантировать точность определения
задержки при наличии шума.
Если посылать более сложный сигнал, состоящий из нескольких импульсов (рис. 2), возникают боковые лепестки, вызванные заданием формы сигнала и увеличением длинны У вдвое.
X1=zeros (1,1000);
Y1=zeros (1,1000);
X1(1:100)=5;
Y1(301:400)=1;
X1(500:600)=3;
Y1(801:900)=1;
C1=conv(X1,Y1);
figure
plot(C1);
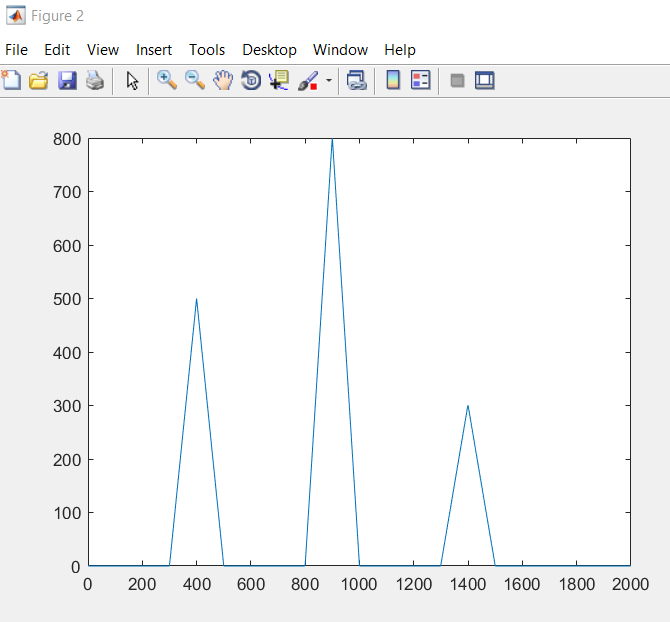
Рисунок 2 – КФ сложного сигнала
С помощью случайной последовательности создаем входной сигнал без периодических повторов импульсов (0 и 1). Задав выходную реакцию, получим график корреляционной функции.
X=rand(1,1000);
for i=1:1000
if X(i)>0.5
X(i)=0;
else X(i)=1;
end
end
Y=zeros (1,1000);
Y(301:400)=2;
My=mean(Y);
figure
plot(conv(X, Y))
hold on
for i=1:900
C(i)=(X(i)-mean(X)).*(Y(i+99)-My);
end
plot(C)
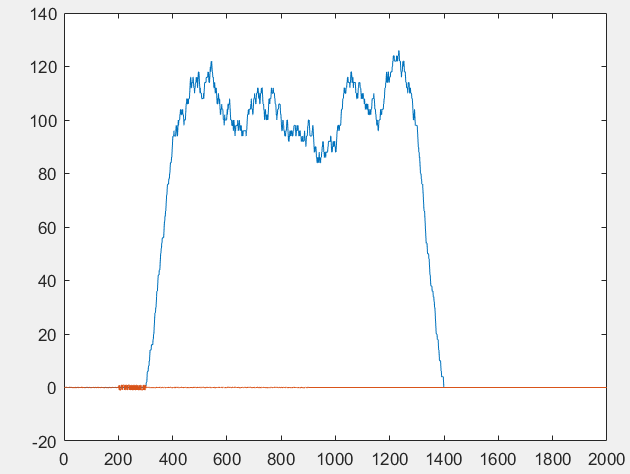
Рисунок 3 – КФ и ковариация
КФ (корреляционная функция), вычисленная по центрированному значению сигнала, представляет собой ковариационную функцию сигнала.
На принятый сигнал наложим шум, с SNR=3; 10 дБ.
%SNR
SNR = 3;
Y=zeros (1,1000);
Y(301:400)=2;
y = randn(size(Y))*std(Y)/db2mag(SNR);
S3 = Y + y;
pulseSNR = snr(Y,y);
figure
subplot(3,1,1)
plot(S3)
SNR=10;
Y=zeros (1,1000);
Y(301:400)=2;
y = randn(size(Y))*std(Y)/db2mag(SNR);
S10 = Y + y;
subplot(3,1,2)
plot(S10)
pulseSNR = snr(Y,y);
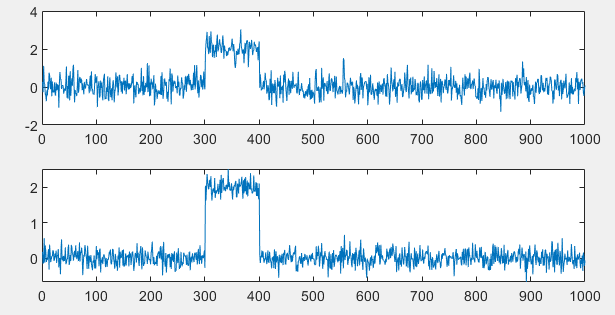
Рисунок 4 – Зашумленный сигнал
Чем больше величина импульса, тем меньшее соотношение сигнала и шума можно использовать.
Наложим шум на синусоиду. Рассмотрим полученный график.
%sin
figure
X=zeros (1,101);
X(1:50)=5;
f=10;
t=0:0.01:1;
Y=sin(2*pi*f*t);
y = randn(size(Y))*std(Y)/db2mag(5);
plot(t,Y)
hold on
Yy=Y+y;
plot(t,Yy)
figure
C=conv(X,Yy);
plot(C);
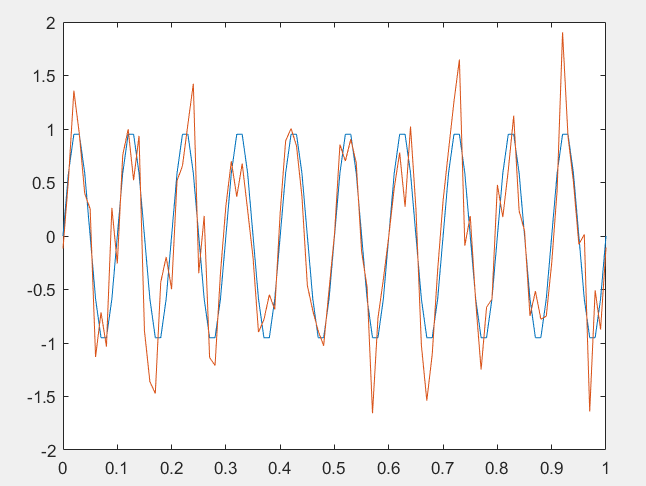
Рисунок 5 – Исходный и зашумленный сигнал
В данном случае соотношение сигнал-шум составляет 5 дБ. Построим КФ (корреляционную функцию)
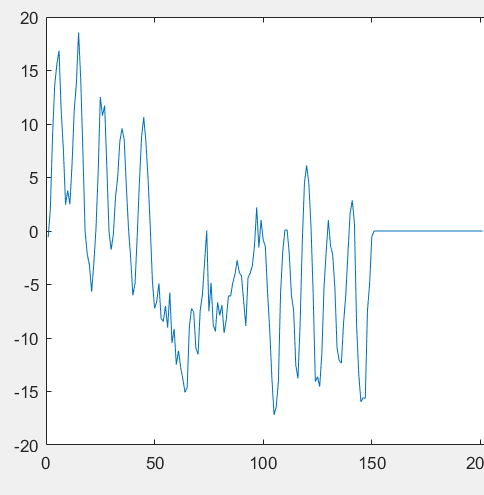
Рисунок 6 – КФ синусоиды
Поскольку максимальное сходство будет в момент полного совпадения сигнала и его копии, по положению максимума корреляционной функции можно судить о времени прихода сигнала.
Вывод:
При выполнении данной лабораторной работы были рассмотрены возможности корреляционного метода для выделения сигнала из шума на примере задачи измерения высоты полета, с импульсами разного задания: единственный, несколько определенных, непериодичная последовательность; зашумление сигнала с заданным соотношением сигнала и шума, а также зашумленный сигнал синусоиды, построены корреляционные функции для каждого из случаев.
Код программы:
close all
clear all
X=zeros (1,1000);
Y=zeros (1,1000);
X(1:100)=5; % излучаемый импульс с амплитудой 5 и длительностью 100 отсчетов
Y(301:400)=1; % принятый импульс запоздал на 300 отсчетов
C=conv(X,Y);
plot(C);
X1=zeros (1,1000);
Y1=zeros (1,1000);
X1(1:100)=5;
Y1(301:400)=1;
X1(500:600)=3;
Y1(801:900)=1;
C1=conv(X1,Y1);
figure
plot(C1);
X=rand(1,1000);
for i=1:1000
if X(i)>0.5
X(i)=0;
else X(i)=1;
end
end
Y=zeros (1,1000);
Y(301:400)=2;
My=mean(Y);
figure
plot(conv(X, Y))
hold on
for i=1:900
C(i)=(X(i)-mean(X)).*(Y(i+99)-My);
end
plot(C)
%SNR
SNR = 3;
Y=zeros (1,1000);
Y(301:400)=2;
y = randn(size(Y))*std(Y)/db2mag(SNR);
S3 = Y + y;
pulseSNR = snr(Y,y);
figure
subplot(3,1,1)
plot(S3)
SNR=10;
Y=zeros (1,1000);
Y(301:400)=2;
y = randn(size(Y))*std(Y)/db2mag(SNR);
S10 = Y + y;
subplot(3,1,2)
plot(S10)
pulseSNR = snr(Y,y);
SNR=0.1;
Y=zeros (1,1000);
Y(301:400)=2;
y = randn(size(Y))*std(Y)/db2mag(SNR);
S1 = Y + y;
subplot(3,1,3)
plot(S1)
pulseSNR = snr(Y,y);
%sin
figure
X=zeros (1,101);
X(1:50)=5;
f=10;
t=0:0.01:1;
Y=sin(2*pi*f*t);
y = randn(size(Y))*std(Y)/db2mag(5);
plot(t,Y)
hold on
Yy=Y+y;
plot(t,Yy)
figure
C=conv(X,Yy);
plot(C);
