Лабораторные / 9091_Боброва Лаб1

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра АПУ

отчЕт

по лабораторной работе №1

«Матричные преобразования и трехмерная графика»

по дисциплине «Математические основы теории систем»

Выполнила: Боброва Н.Ю.

Факультет: ФКТИ

Группа № 9091

Преподаватель: Каплун Д.И.

Санкт-Петербург

2022

ЛАБОРАТОРНАЯ РАБОТА №1.

МАТРИЧНЫЕ ПРЕОБРАЗОВАНИЯ И ТРЕХМЕРНАЯ ГРАФИКА

Цель работы: освоение специфики матричных преобразований

MATLAB и сравнительный анализ различных форм графического отображения результатов.

Основные теоретические сведения:

Матричные операции, вычисление функций от матриц. Кратко напомним основные матричные операции.

Определитель Δ:

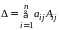
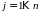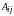, – алгебраическое дополнение;

Обратная матрица :

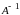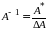
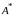– союзная матрица;

Умножение матриц 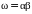. Элемент результирующей матрицы 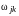на пересечении строки j и столбца k равен сумме попарных произведений элементов строки j матрицы α и столбца k матрицы β:

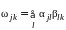
Возведение в степень 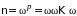осуществляется p‑кратным умножением матрицы на себя.

Ход работы.

В качестве исходной фигуры для выполнения работы выбирается пирамида. Так как матрица, на которой она построена, симметрична относительно главной диагонали, что делает ее вырожденной, добавим к исходной матрице единичную.

R=max(abs(X),abs(Y));

surf(X,Y,-R);

Rr=R+eye(21);

Исходная матрица представлена на рисунке 1.

Рисунок 1 - Пирамида

Сравнение матричных операций.

Сравниваем по имеющимся графикам результаты двух выполненных операций – это обращения матрицы командой inv и поэлементного деления матрицы ones(n,n) на R. Результат представлен на рисунке 2.

Detr=det(Rr);

Inv=inv(Rr);

O=ones(size(Rr))./(-Rr);

figure

subplot(2,1,1)

surf(X,Y,Inv);

subplot(2,1,2)

surf(X,Y,O);

Рисунок 2 – Результат обращения матрицы командой inv и поэлементного деления матрицы ones(n,n) на R

%kv koren

S1=abs(sqrtm(Rr));

S2=Rr.^(1/2);

figure

subplot(2,1,1)

surf(X,Y,-S1);

subplot(2,1,2)

surf(X,Y,-S2);

%logarifm

L1=abs(logm(Rr));

L2=log(Rr);

figure

subplot(2,1,1)

surf(X,Y,-L1);

subplot(2,1,2)

surf(X,Y,-L2);

%exponenta

E1=expm(Rr);

E2=exp(Rr);

figure

subplot(2,1,1)

surf(X,Y,-E1);

subplot(2,1,2)

surf(X,Y,-E2);

При реализации матричных операций поверхность является гладкой, в отличие от поэлементного осуществления соответствующей операции.

Изменение формы пирамиды обнулением значений, заданных первой строкой следующего элемента кода:

Rr(:,10:14)=0;

figure

subplot(2,1,1)

mesh(-Rr)

Rr(18:20,:)=3;

subplot(2,1,2)

mesh(-Rr)

surfl(-Rr) % освещенная поверхность (без каркасной сетки)

shading interp % линейное изменение цвета

colormap('gray') % палитра серого

На рисунке поверхность представлена 2мя способами: каркас и заполненная поверхность.

Операция кронекеровского умножения матриц, в которой вся правая матрица умножается на каждый элемент левой:

%kronv

Z=[3 3 3 4 4 4 5 5 5];

k=kron(Z, -R);

figure

surf(k);

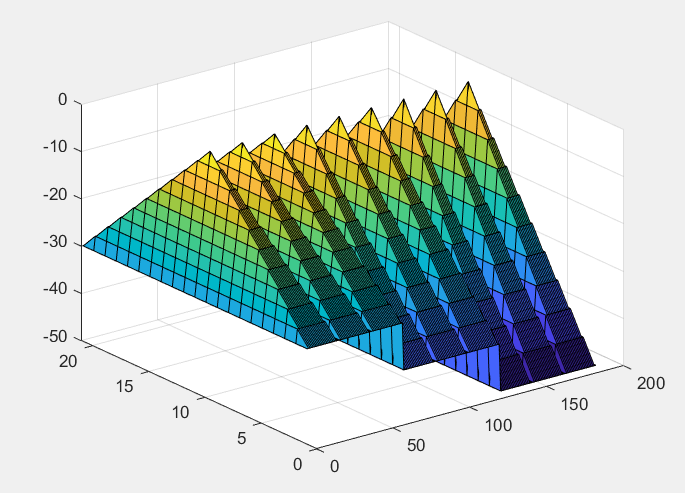
При изменении порядка записи матриц число полученных масивов равно числу элементов матрицы R (21):

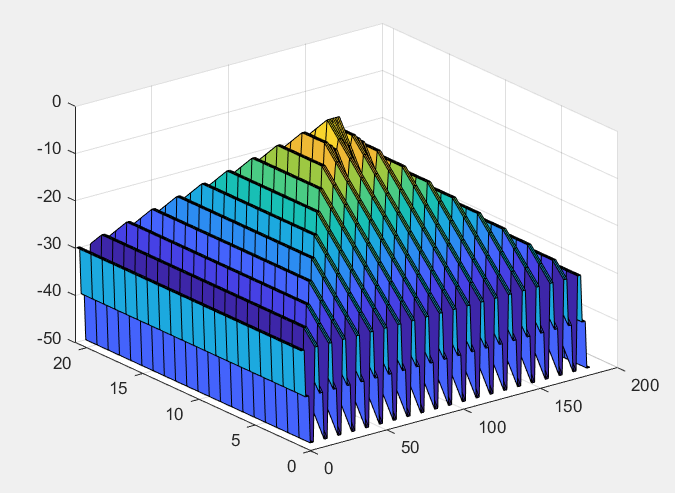
Вывод:

В данной лабораторной работе, путем работы с исходно предоставленной фигурой были изучены матричные преобразования: поэлементные и матричные операции, сравнения графиков выполненных операций, обращения матрицы и ее поэлементарного деления. Так же были изучены матричные операции sqrtm(A), logm(A), expm(A) с их аналогичными операциями. Освоена была операция врезки пирамиды, и операция размножения массивов путем умножения матриц.

Код программы

close all

clear all

x=-10:10;

y=ones(1,21);

X=x'*y;

Y=y'*x;

%пирамида

R=max(abs(X),abs(Y));

surf(X,Y,-R);

Rr=R+eye(21);

Det=det(R);

Rr=R+eye(21);

Detr=det(Rr);

Inv=inv(Rr);

O=ones(size(Rr))./(-Rr);

figure

subplot(2,1,1)

surf(X,Y,Inv);

subplot(2,1,2)

surf(X,Y,O);

%kv koren

S1=abs(sqrtm(Rr));

S2=Rr.^(1/2);

figure

subplot(2,1,1)

surf(X,Y,-S1);

subplot(2,1,2)

surf(X,Y,-S2);

%logarifm

L1=abs(logm(Rr));

L2=log(Rr);

figure

subplot(2,1,1)

surf(X,Y,-L1);

subplot(2,1,2)

surf(X,Y,-L2);

%exponenta

E1=expm(Rr);

E2=exp(Rr);

figure

subplot(2,1,1)

surf(X,Y,-E1);

subplot(2,1,2)

surf(X,Y,-E2);

Rr(:,10:14)=0;

figure

subplot(2,1,1)

mesh(-Rr)

Rr(18:20,:)=3;

subplot(2,1,2)

mesh(-Rr)

surfl(-Rr) % освещенная поверхность (без каркасной сетки)

shading interp % линейное изменение цвета

colormap('gray') % палитра серого

%kronv

Z=[3 3 3 4 4 4 5 5 5];

k=kron(Z, -R);

figure

surf(k);

figure

surf(kron(-R, Z));