37.
Проверка гипотезы об однородности
двух выборок по критерию знаков.
На
практике встречаются ситуации, когда
требуется проверить отсутствие
изменений в законе распределения НСВ
ξ. Такие изменения могут возникнуть,
когда меняются условия проведения
случайного эксперимента. Различного
вида гипотезы об отсутствии изменений
в законе распределения НСВ ξ называют
гипотезой
однородности.
 Одним
из наиболее простых критериев проверки
гипотезы однородности является
критерий
знаков.
Пусть Х
= [X1,X2,…Xn]T
и Y=[Y1,Y2,…,Yn]T
– выборки
из распределения двух НСВ ξ и η с
функциями распределения Fξ
и Fη.
По гипоттезе Н0
: Fξ=Fη
Будем
полагать, что выборки Х
и Y
не содержат
одинаковых соответствующих по номеру
элементов. В противном случае эти
совпадающие элементы из выборок
исключаем.
Построим новую выборку
Z=[Z1,Z2,…Zn1]T,
Одним
из наиболее простых критериев проверки
гипотезы однородности является
критерий
знаков.
Пусть Х
= [X1,X2,…Xn]T
и Y=[Y1,Y2,…,Yn]T
– выборки
из распределения двух НСВ ξ и η с
функциями распределения Fξ
и Fη.
По гипоттезе Н0
: Fξ=Fη
Будем
полагать, что выборки Х
и Y
не содержат
одинаковых соответствующих по номеру
элементов. В противном случае эти
совпадающие элементы из выборок
исключаем.
Построим новую выборку
Z=[Z1,Z2,…Zn1]T,
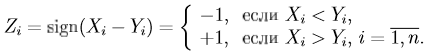 Найдем распределение Zk,
когда верна гипотеза Н0.
Так как случайные величины Xk
и Yk
независимы и их распределение одинаково,
то распределение Zk
имеет вид табл 3.6.
Таким образом,
выборку Z
можно рассматривать как последовательность
успехов (Zi=1)
и неудач (Zi=-1)
в n
испытаниях Бернулли с вероятностью
успеха р=1/2 в одном испытании. Если
Найдем распределение Zk,
когда верна гипотеза Н0.
Так как случайные величины Xk
и Yk
независимы и их распределение одинаково,
то распределение Zk
имеет вид табл 3.6.
Таким образом,
выборку Z
можно рассматривать как последовательность
успехов (Zi=1)
и неудач (Zi=-1)
в n
испытаниях Бернулли с вероятностью
успеха р=1/2 в одном испытании. Если
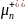 - число успехов в n
испытаниях, то распределение
-
биноминальное с вероятностью успеха
р=1/2:
- число успехов в n
испытаниях, то распределение
-
биноминальное с вероятностью успеха
р=1/2:
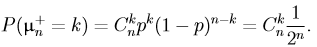 Если взять
в качестве критериальной функции, то
критическая область Q(α) строится
следующая образом. Выберем число rα
так,
чтобы выполнялись условия:
Если взять
в качестве критериальной функции, то
критическая область Q(α) строится
следующая образом. Выберем число rα
так,
чтобы выполнялись условия:
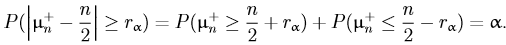 При
этом в силу симметрии
При
этом в силу симметрии
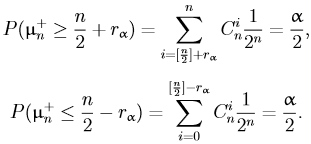 Если |
Если |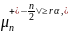 то
гипотеза H0
отклоняется.
Для перехода к
односторонней критической области
обозначим
то
гипотеза H0
отклоняется.
Для перехода к
односторонней критической области
обозначим
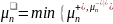 ,
где
,
где
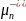 =n-
.
Тогда критерий принимает вид:
если
=n-
.
Тогда критерий принимает вид:
если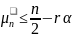 ,
то Н0
отколняется.
Для выбора значения
rα
имеются
специальные таблицы, рассчитываемы
по формулам биноминального распределения.
,
то Н0
отколняется.
Для выбора значения
rα
имеются
специальные таблицы, рассчитываемы
по формулам биноминального распределения.

|
38.
Лемма Неймана-Пирсона.
Лемма.
При
сделанных ранее предположениях
существует наиболее мощный критерий
проверки гипотезы Н0
против альтернативы Н1
с критической областью Q*(
)={X:Ln(x)≥
}
где порог cα
определяется
условием
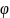 (cα)
= α.
Док-во.
Рассмотрим
любой другой критерий уровня значимости
α1 определяемый
критической областью Q(α) (рис.3.7). Его
мощность
(cα)
= α.
Док-во.
Рассмотрим
любой другой критерий уровня значимости
α1 определяемый
критической областью Q(α) (рис.3.7). Его
мощность
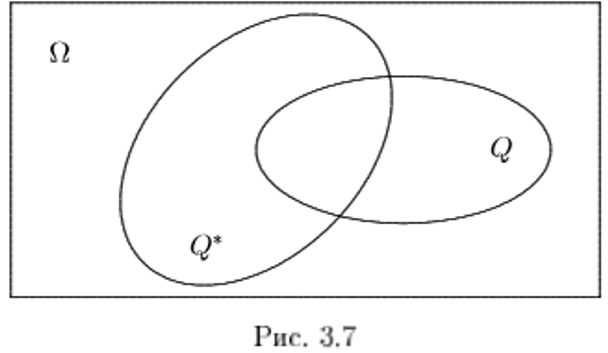
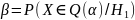 =
=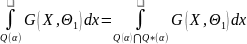 +
+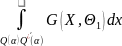 .
.
Аналогично
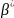 =
= +
+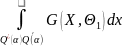
Тогда
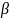 =
-
=
-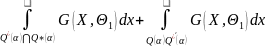 В точках множества Q*(
)
Ln(x)≥
,
в точках множества
В точках множества Q*(
)
Ln(x)≥
,
в точках множества
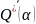 Ln(X)<c.Значит,
Ln(X)<c.Значит,
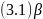 =
+
=
+ +
+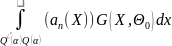 ≤
-
≤
-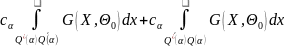 =
=
+
(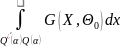 -
-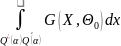 )
)
По
условию P(X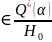 )=p(X
)=p(X )=α
,или
)=α
,или
(3.2)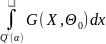 =
=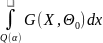 =α
=α
Область
интегрирования в (3.1) в одном интеграле
представляет собой (рис 3.7) Q(α)/(
Q(α)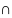 Q*(
α)), а во втором- Q*(α)/(
Q(α)
Q*(
α)),поэтому каждый из интегралов в
(3.1), с учетом (3.2),отлтчается от α на
величину
Q*(
α)), а во втором- Q*(α)/(
Q(α)
Q*(
α)),поэтому каждый из интегралов в
(3.1), с учетом (3.2),отлтчается от α на
величину
 Значит
сумма интегралов в (3.1) равна нулю и
Значит
сумма интегралов в (3.1) равна нулю и
β
≤ β∗,
т.е. критерий Q∗- наиболее мощный.

Критерий
Неймана-Пирсона часто называют также
критерием
отношения правдоподобия.
______________________________________________
На
счет критерия Н-П(отдельно).
Наилучшим
критерием с точки зрения его мощности
является РНМ-критерий. К сожалению,
РНМ-критерии сущ., скорее, как исключения
лишь в некоторых простых случаях.
Вместе с тем, если рассматривать задачу
выбора из двух простых параметрическиских
гипотез (при заданных основной гипотез
(при заданных основной гипотезе Н0
и альтернативной Н1),
то можно доказать существование
наиболее мощного критерия. Такой
критерий носит название критерия
Неймана-Пирсона.
|
|
|
|
|


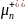 - число успехов в n
испытаниях, то распределение
-
биноминальное с вероятностью успеха
р=1/2:
- число успехов в n
испытаниях, то распределение
-
биноминальное с вероятностью успеха
р=1/2: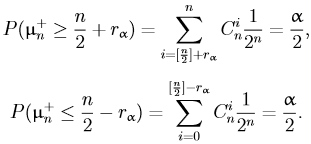 Если |
Если |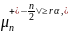 то
гипотеза H0
отклоняется.
Для перехода к
односторонней критической области
обозначим
то
гипотеза H0
отклоняется.
Для перехода к
односторонней критической области
обозначим
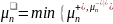 ,
где
,
где
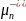 =n-
.
Тогда критерий принимает вид:
если
=n-
.
Тогда критерий принимает вид:
если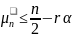 ,
то Н0
отколняется.
Для выбора значения
rα
имеются
специальные таблицы, рассчитываемы
по формулам биноминального распределения.
,
то Н0
отколняется.
Для выбора значения
rα
имеются
специальные таблицы, рассчитываемы
по формулам биноминального распределения.

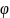 (cα)
= α.
Док-во.
Рассмотрим
любой другой критерий уровня значимости
α1 определяемый
критической областью Q(α) (рис.3.7). Его
мощность
(cα)
= α.
Док-во.
Рассмотрим
любой другой критерий уровня значимости
α1 определяемый
критической областью Q(α) (рис.3.7). Его
мощность

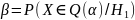 =
=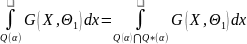 +
+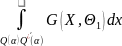 .
.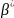 =
= +
+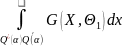
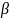 =
-
=
-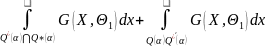 В точках множества Q*(
)
Ln(x)≥
,
в точках множества
В точках множества Q*(
)
Ln(x)≥
,
в точках множества
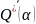 Ln(X)<c.Значит,
Ln(X)<c.Значит,
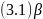 =
+
=
+ +
+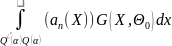 ≤
-
≤
-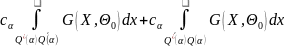 =
=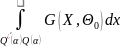 -
-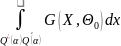 )
)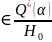 )=p(X
)=p(X )=α
,или
)=α
,или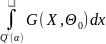 =
=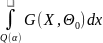 =α
=α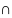 Q*(
α)), а во втором- Q*(α)/(
Q(α)
Q*(
α)),поэтому каждый из интегралов в
(3.1), с учетом (3.2),отлтчается от α на
величину
Q*(
α)), а во втором- Q*(α)/(
Q(α)
Q*(
α)),поэтому каждый из интегралов в
(3.1), с учетом (3.2),отлтчается от α на
величину
 Значит
сумма интегралов в (3.1) равна нулю и
Значит
сумма интегралов в (3.1) равна нулю и
