
ТВиМС ответы на экзамен
.docx1.Вероятностное пространство. Аксиоматика А.Н. Колмогорова. Пусть
F
– некоторая система подмножеств
множества Ω,
1.Ω 2.Если
A
3.Если
Если
аксиома 3 выполняется в счетном
варианте, т.е. если
Пусть на множестве элементарных событий Ω задана – алгебра (или F в случае конечного множества событий) его подмножеств. Элементы – алгебры (алгебры - F) называется событием на Ω. Говорят,
что на алгебре событий F
задано вероятностное
распределение
Р, если каждому событию A
4.0≤ Р(А) ≤ 1 5.Р(Ω) = 1 6.Если
А,
и
Если вероятностное распределение задается на – алгебре, то аксиома 6, называется аксиомой аддитивности, формируется в системном варианте: 6a
– если
Тройка (Ω, F, P) обычно называется вероятностным пространством.
|
2.Типы вероятностных пространств. Дискретное ВП: соответствует случаю дискретного пространства элементарных событий, который рассматривается в элементарной теории. Множество
элементарных событий
Вероятность
распределения Р определяется набором
вероятностей элементарных событий
Непрерывное ВП: Множество
событий Ω= Абсолютно непрерывное ВП – ВП, в котором вероятностное распределение задается с помощью специальной функции – плотности распределения. Говорят,
что функция f
(
Тогда вероятностное распределение на F определяется так:
Смешанное ВП конструируется объединением дискретного и непрерывного ВП. Ввиду некоторой искусственности подобной конструкции в дальнейшем этот тип ВП рассматриваться не будет.
|
3.Случайные события. Операции над событиями. Теоремы сложения. Случайный эксперимент – эксперимент, в котором наблюдается устойчивость частот. Все
взаимоисключающие исходы эксперимента
Конечное или счетное множество элементарных событий называется дискретным пространством элементарных событий. Любое подмножество дискретного пространства элементарных событий называется событием. Пусть Ω – дискретное пространство элементарных событий, А, В, С – события. Дадим вероятностную интерпретацию некоторых фактов теории множеств: •
•
•
Суммой
событий
А и В называется событие С, содержащее
все исходы
Произведением
событий
А и В называется событие С, состоящее
из исходов, благоприятных как для
события А, так и для события В,
обозначается
Разностью
событий
А и В называется событие С, состоящее
из исходов, благоприятных для события
А, но неблагоприятных событию В,
обозначается
События
А и В называются несовместимыми,
если они не имеют общих исходов, т.е.
если
Событие
С называется противоположным
событию А, если С состоит из всех
исходов, неблагоприятных для А
(дополняет А до Ω), обозначается
Пусть
Ω – пространство элементарных событий,
Р – вероятностное распределение на
Ω. Рассмотрим как связаны вероятности
Р(А), Р(В) событий А и В и вероятность
Теорема: Если события А и В несовместны, то вероятность суммы событий равна сумме их вероятностей.
Доказательство:
На основании аксиомы аддитивности:
Теорема сложения: Для
любых событий А и В:
Доказательство:
Для графического представления подобных тождеств использую диаграмму Венна. Мы
представим сумму событий А и В попарно
несовместными событиями. Используя
предыдущую теорему
С
другой стороны:
|
4.Условная вероятность. Формула полной вероятности. Формула Байеса. 1.
Пусть Ω – пространство элементарных
событий с вероятностным распределением
Р. Пусть А и В – некоторые события на
Ω , причем Р(А)
Теорема
умножения:
2.
Пусть А – произвольное событие, а
события
Доказательство:
События A
можно представить в виде суммы попарно
несовместных обытий:
3.
Формула
Байеса: Запишем
определение условной вероятности
события
|
5. Независимые испытания. События
А и В называются независимыми,
если выполнено равенство
Теорема:
Если события А и В независимы, то
события
Доказательство:
Следствия: 1.Если
события А и В независимы, то события
2.Если для событий А и В не выполнено условие , то они называются зависимыми. События
Рассмотрим
эксперимент, состоящий из двух частей.
Первый описывается пространством
элементарных событий
Если
модель сложного эксперимента построена
так, что для любого события
Теорема:
Пусть
Определим
Р (( 1.Р(•) есть распределение вероятностей на Ω; 2.События
3.События
Доказательство: 1.Согласно
определению вероятности события
2.Для
вероятности
Аналогично
для Р( 3.Запишем вероятность произведения событий :
|
6. Дискретная случайная величина и ее числовые характеристики Случайной
величиной
X(ω)
называется функция X:
Ω → R,
заданная на множестве элементарных
событий Ω вероятностного пространства
(Ω, F,
P),
такая, что для любого события {ω | X
(ω)
Функцией
распределения
случайной величины X
называется функция
Функция распределения имеет следующие свойства: 1.
Набор
значений
Ряд распределения должен обладать следующими свойствами:
Математическим
ожиданием
случайной величины X
называется число
Если
X
– дискретная случайная величина, то
математическое ожидание
Существует
равенство:
Покажем,
что математическое ожидание обладает
свойством
В качестве интегральных числовых характеристик случайной величины обычно используются начальные и центральные моменты. Начальным
моментом порядка
k
называется число
Центральным
моментом
порядка k
называется число
Центральный момент второго порядка называется дисперсией:
В
случае дискретной случайной величины
с рядом распределения
Если математическое ожидание – это в некотором смысле среднее значение случайной величины, то дисперсия – это средний квадрат отклонения от среднего. Для
любы вещественных чисел a
и b
справедливо
Для вычисления дисперсии иногда удобнее применять формулу:
|
7. Абсолютно-непрерывная случайная величина и ее числовые характеристики. Случайной величиной X(ω) называется функция X: Ω → R, заданная на множестве элементарных событий Ω вероятностного пространства (Ω, F, P), такая, что для любого события {ω | X (ω) принадлежит F. Функцией распределения случайной величины X называется функция , которая каждому значению X ставит в соответствие число Функция распределения имеет следующие свойства:
неубывающая функция; непрерывна слева, т.е. в любой точке а левосторонний предел равен значению функции; . Случайная
величина X
называется абсолютно непрерывной,
если существует такая функция f(x),
что для любого борелевского множества
А на прямой Р 1.f(x) 2. Математическим ожиданием случайной величины X называется число , где F(x) – функция распределения случайной величины X. Если
X
– абсолютно непрерывная случайная
величина, то математическое ожидание
Существует равенство: (док-во стр. 40 метода). Покажем, что математическое ожидание обладает свойством . В качестве интегральных числовых характеристик случайной величины обычно используются начальные и центральные моменты. Начальным моментом порядка k называется число Центральным моментом порядка k называется число ,
Центральный момент второго порядка называется дисперсией:
В случае абсолютно непрерывной случайной величины с плотностью распределения f(x):
Если математическое ожидание – это в некотором смысле среднее значение случайной величины, то дисперсия – это средний квадрат отклонения от среднего. Для любы вещественных чисел a и b справедливо
Для вычисления дисперсии иногда удобнее применять формулу:
|
8. Дискретный случайный вектор. Мат. ожидание и ковариационная матрица. Пара
случайных величин Х1 , Х2 называется
случайным вектором. Случайный вектор
называется дискретным, если множество
его возможных значений конечно или
счетно. Обозначение : Чтобы задать случайный вектор, нужно перечислить : все возможные значения Х1 - х11, х12, ... , x1n ; все возможные значения Х2 - x21, x22, … , x2m ; и задать вероятности всех событий Hij = {X1 = x1i}*{X2 = x2j}, которые составляют полную систему событий. Будем обозначать pij = P(Hij). Все эти данные удобно расположить в таблице.
Tеорема (свойства рij) Для того, чтобы рij были распределением вероятностей дискретного случайного вектора =(x1x2) необходимо и достаточно выполнение условий : (1)
pij≥0
(2)
Математическое ожидание Пусть (ξ, η ) - двумерная случайная величина, тогда M(ξ,η)=(M(ξ), M(η)), т.е. математическое ожидание случайного вектора - это вектор из математических ожиданий компонент вектора.Если (ξ, η) - дискретный случайный вектор с распределением(схема сверху,только x11 весь ряд y,а ряд x21 –просто x ) То
математические ожидания компонент
вычисляются по формулам:Mξ= Mη
= Если p(ξ,η)(x, y)- совместная плотность распределения непрерывной двумерной случайной величины (ξ,η), то Mξ= Поскольку Ковариация Если между случайными величинами ξ и η существует стохастическая связь, то одним из параметров, характеризующих меру этой связи является ковариация cov(ξ,η). Ковариацию вычисляют по формулам cov(ξ,η)=M[(ξ - M ξ )( η - M η)] = M(ξ η)-Mξ Mη Если случайные величины ξ и η независимы, то cov(ξ, η )=0.Обратное, вообще говоря, неверно. Из равенства нулю ковариации не следует независимость случайных величин. Случайные величины могут быть зависимыми в то время как их ковариация нулевая! Но зато, если ковариация случайных величин отлична от нуля, то между ними существует стохастическая связь, мерой которой и является величина ковариации.Свойства ковариации: cov(ξ, ξ) = D ξ; cov(ξ+C1, η+C2)= cov(ξ, η ); cov(ξ, η)= cov(η, ξ); cov(C1 ξ+C2 η, ς)=C1cov(ξ, ς)+C2cov(η, ς) где C1 и C2 - произвольные константы. Ковариационной матрицей случайного вектора (ξ,η) называется матрица вида:
Эта матрица симметрична и положительно определена. Ее определитель называется обобщенной дисперсией и может служить мерой рассеяния системы случайных величин (ξ,η). Как
уже отмечалось ранее, дисперсия суммы
независимых случайных величин равна
сумме их дисперсий:D(ξ+
η)=D(ξ)+D(η).
Если же случайные величины зависимы,
то D(ξ |
9. Абсолютно-непрерывный случайный вектор. Мат. ожидание и ковариационная матрица. Говорят
,что случайный вектор имеет абсолютно
непрерывное распределение,если
существует функция т переменных
f(x1,…,xn),такая,что
для любого борелевского множества A
из
.P( B= B=
|
10. Корреляционная матрица случайного вектора. Коэффициент корреляции двух случайных величин. R= D=b2-ac=cov2(x1,x2)-D(x1)D(x2)≤0
⤇ R= Если коэф корреляции = 0⤇2 случ величины наз некорреляционными.
|
11. Независимость случайных величин. Случайные
величины X1
и X2
называются независимыми, если
независимыми являются любые события
вида {X1 P(X1 A1; X2 A2)=P(X1 A1)P(X2 A2) А для дискретных случайных величин : P(X1=xi;X2=yj)=P(X1=xi)P(X2=yj) Взяв в качестве A1 и A2 интервалы [-∞,x1) и [-∞,x2),получим,что функция распределения случайного вектора (X1,X2) равна произведению функций распределения входящего в него независимых случ величин: F(x1,x2)=F1(x1)F2(x2).Если распределения независимых случ величин являются абсолютно непрерывными ,то, продифференцировав последнее равенство по переменным x1 и x2 , получим соответствующую связь плотности распределения случайного вектора с плотностями компонент:f(x1,x2)=f1(x1)f2(x2). Полученные формулы разложения в произведение для функций распределения или плотностей являются не только необходимыми ,но и достаточными условиями независимости:при их выполнении для всех значений переменных, соответствующих случайные величины являются независимыми.Математическое ожидание произведения независимых случ величин равно произведению их математических ожиданий . Доказательство проведем для абсолютно непрерывных случ величин. Пусть X1 и X2 - независимые случ величины. Тогда: M{X1X2}=
= Из этой формулы вытекает важное следствие:ковариационный момент независимых случ величин равен 0.Ковариционный момент: Cov(X1,X2)= M{X1X2}- M{X1}M{X2}= M{X1}M{X2}- M{X1}M{X2}=0 Случайные величины называются некоррелированными, если их ковариационный момент (и, соответственно ,коэффициент корреляции) равен 0.Таким образом ,из независимости случайных величин следует их некоррелированность.(обратное в общем случае неверно).
|
12. Распределение суммы двух случайных величин. Пусть
ξ1
и ξ2
— случайные величины с плотностью
совместного распределения fξ1,ξ2(x1,x2)
, и задана борелевская функция g: Пользуясь тем, что вероятность случайному вектору попасть в некоторую область можно вычислить как объем под графиком плотности распределения вектора над этой областью, сформулируем утверждение. Теорема
1.Пусть x Fη(x)=P((ξ1,ξ2)
Dx)= Далее в этой главе предполагается, что случайные величины ξ1 и ξ2 независимы, т.е.f ξ1, ξ2(x1,x2)≡ f ξ1(x1) f ξ1 (x2). В этом случае распределение величины g(x1,x2) полностью определяется частными распределениями величин ξ1 и ξ2. Следствие (формула сверстки). Если случайные величины ξ1 и ξ2 независимы и имеют абсолютно непрерывные распределения с плотностями f ξ1(x1) и f ξ2(x2) , то плотность распределения суммы ξ1+ ξ2 равна «свёртке» плотностей f ξ1 и f ξ2 : f ξ1+ ξ2(t)= ξ1(u) f ξ2(t-u)du= ξ2(u) f ξ1(t-u)du Доказательство.
Воспользуемся утверждением теоремы
1 для борелевской функции g(x1,x2)=x1+x2
. Интегрирование по области
Dx={(x1,x2)|x1+x2<x}
можно заменить последовательным
вычислением двух интегралов: наружного
— по переменной x1,
меняющейся в пределах от
Сделаем в последнем интеграле замену переменной x2 на t так: x2=t-x1 . При этом x2 ( ,x-x1) перейдёт в t ( ,x), dx2=dt . В полученном интеграле меняем порядок интегрирования: функция распределения Fξ1+ξ2(x) равна
Итак,
мы представили функцию распределения
Fξ1+ξ2(x)
в виде
Второе равенство получается либо из первого заменой переменных, либо просто из-за возможности поменять местами ξ1 и ξ2 . Следствие 9 не только предлагает формулу для вычисления плотности распределения суммы, но и утверждает (заметьте!), что сумма двух независимых случайных величин с абсолютно непрерывными распределениями также имеет абсолютно непрерывное распределение.
|

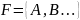 ,
A
,
A
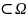 ,
B⊂Ω,
… Множество F
называется алгеброй,
если выполнены следующие условия
(аксиомы):
,
B⊂Ω,
… Множество F
называется алгеброй,
если выполнены следующие условия
(аксиомы):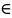 F
F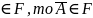
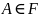 и
и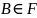 , то
, то
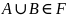 и A
и A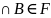
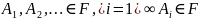 и
и
 , то алгебра F
называется
, то алгебра F
называется
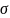 – алгеброй
(сигма - алгеброй).
– алгеброй
(сигма - алгеброй).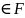 поставлено в соответствии число Р(А),
называемое вероятностью события А,
причем выполнены следующие аксиомы:
поставлено в соответствии число Р(А),
называемое вероятностью события А,
причем выполнены следующие аксиомы:
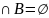 ,то
,то
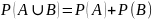 .
.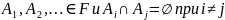 ,
то
,
то
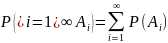
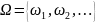 - дискретное множество, т.е. конечное
или счетное. В качестве
– алгебры F
всегда берется
- дискретное множество, т.е. конечное
или счетное. В качестве
– алгебры F
всегда берется
 – множество всех подмножеств Ω.
– множество всех подмножеств Ω.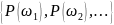 ,
,
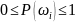
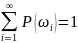 и
правилом вычисления вероятностей
любого события
и
правилом вычисления вероятностей
любого события
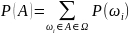
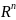 ,
– алгебра событий F
есть борелевская
– алгебра
,
– алгебра событий F
есть борелевская
– алгебра
 ,
порожденная n-мерными
клетками
,
порожденная n-мерными
клетками
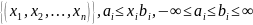 i=1,2,3,…,n.
ВП задается на элементах F.
i=1,2,3,…,n.
ВП задается на элементах F.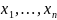 ),
отображающая
в R,
является плотностью
распределения вероятности
в следующих случаях:
),
отображающая
в R,
является плотностью
распределения вероятности
в следующих случаях: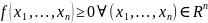

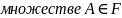
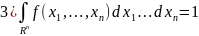
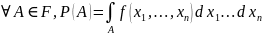 .
.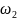 называются элементарными
событиями.
Будем считать, что множество элементарных
событий Ω конечно или счетно, т.е. Ω=
называются элементарными
событиями.
Будем считать, что множество элементарных
событий Ω конечно или счетно, т.е. Ω=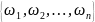 или
или

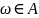 (элемент
(элемент
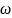 принадлежит множеству А) – исход
благоприятен для события А;
принадлежит множеству А) – исход
благоприятен для события А;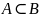 (множество
А содержится во множестве В) – событие
А влечет за собой событие В.
(множество
А содержится во множестве В) – событие
А влечет за собой событие В.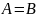 (множества
А и В равные) – события А и В состоят
из одних и тех же элементарных событий.
(множества
А и В равные) – события А и В состоят
из одних и тех же элементарных событий. ,
благоприятные либо событию А, либо
событию В, обозначается
,
благоприятные либо событию А, либо
событию В, обозначается
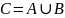 .
.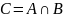 .
.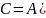 .
.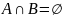 .
.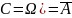 .
.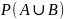 их суммы
их суммы
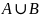 .
.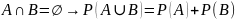
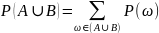 ,
с учетом
,
с учетом
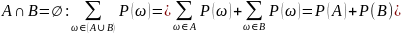
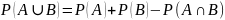
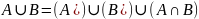
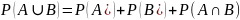
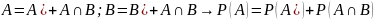
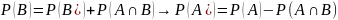
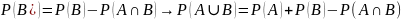
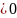 .
Тогда число Р(В/А)=
.
Тогда число Р(В/А)= называется условной
вероятностью события В
при условии, что событие А наступило
(коротко говорят «вероятностью В при
условии А»).
называется условной
вероятностью события В
при условии, что событие А наступило
(коротко говорят «вероятностью В при
условии А»).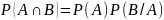 .
.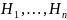 попарно несовместны (
попарно несовместны (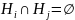 при
при
 ),
причем
),
причем
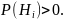 Пусть
Пусть
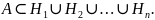 Тогда справедлива следующая формула,
которую называют формулой
полной вероятности:
Тогда справедлива следующая формула,
которую называют формулой
полной вероятности: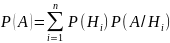
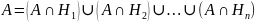 .
Тогда в соответствии с теоремой
сложения:
.
Тогда в соответствии с теоремой
сложения:
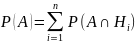 и в соответствии с теоремой умножения:
.
и в соответствии с теоремой умножения:
.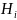 при условии, что событие А наступило:
при условии, что событие А наступило:
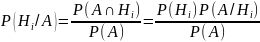 .
Заменим P(A)
через формулу полной вероятности:
.
Заменим P(A)
через формулу полной вероятности:
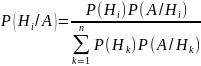 .
Это и есть формула Байеса.
.
Это и есть формула Байеса.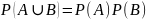 .
.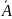 и В также независимые:
и В также независимые:
 ,
тогда
,
тогда
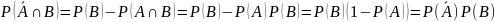 .
.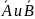 также независимы.
также независимы.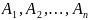 называются независимыми
в совокупности,
если для любого k
из них (
называются независимыми
в совокупности,
если для любого k
из них ( )
выполняется условие:
)
выполняется условие:
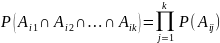 ,
если соотношение выполняется
справедливо при k=2,
то события попарно
независимы.
,
если соотношение выполняется
справедливо при k=2,
то события попарно
независимы.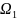 с вероятностным распределением
с вероятностным распределением
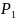 ,
а второй -
,
а второй -
 с распределением
с распределением
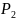 .
.
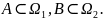 Требуется построить модель эксперимента
так, чтобы события
Требуется построить модель эксперимента
так, чтобы события
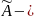 «в первой части произошло событие А»
и
«в первой части произошло событие А»
и
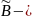 «во второй части произошло событие
В» были независимы.
«во второй части произошло событие
В» были независимы.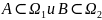 события
события
 независимы то говорят, что эксперимент
состоит из двух независимых
испытаний.
независимы то говорят, что эксперимент
состоит из двух независимых
испытаний.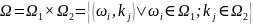
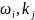 ))
=
))
=
 .
Тогда:
.
Тогда: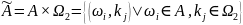 и
и
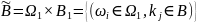 имеют вероятности
имеют вероятности
 .
.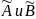 независимы.
независимы.
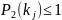 ,
значит,
,
значит,
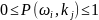 .
Тогда:
.
Тогда:
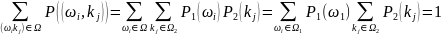 ,
т.е. действительно Р(•) задает на Ω
распределение вероятностей
,
т.е. действительно Р(•) задает на Ω
распределение вероятностей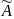 :
: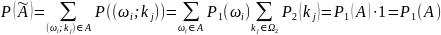
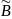 ).
).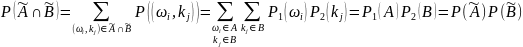
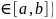 принадлежит F.
принадлежит F.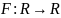 ,
которая каждому значению X
ставит в соответствие число
,
которая каждому значению X
ставит в соответствие число

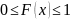 ;
;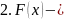 неубывающая
функция;
неубывающая
функция; непрерывна
слева, т.е. в любой точке а левосторонний
предел равен значению функции;
непрерывна
слева, т.е. в любой точке а левосторонний
предел равен значению функции;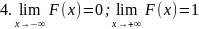 .
.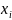 вместе с вероятностями
вместе с вероятностями
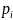 называется рядом
распределения дискретной случайной
величины.
называется рядом
распределения дискретной случайной
величины.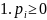 ;
; .
. ,
где F(x)
– функция распределения случайной
величины X.
,
где F(x)
– функция распределения случайной
величины X.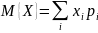 .
По сути математическое ожидание –
это координата тяжести вероятностного
распределения.
.
По сути математическое ожидание –
это координата тяжести вероятностного
распределения.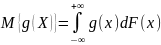 (док-во
стр. 40 метода).
(док-во
стр. 40 метода).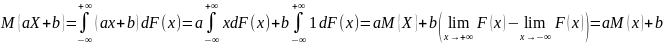 .
.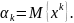
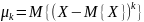 ,
,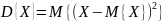
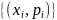
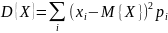
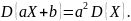
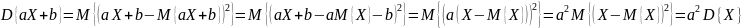 .
.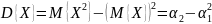
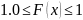 ;
;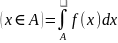 .
Вероятностное пространство, на котором
задана такая случайная величина,
является абсолютно непрерывным с
плоскостью f(x).
Эта плотность удовлетворяет следующим
свойствам:
.
Вероятностное пространство, на котором
задана такая случайная величина,
является абсолютно непрерывным с
плоскостью f(x).
Эта плотность удовлетворяет следующим
свойствам: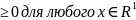 ;
;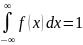
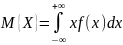 .
По сути математическое ожидание –
это координата тяжести вероятностного
распределения.
.
По сути математическое ожидание –
это координата тяжести вероятностного
распределения.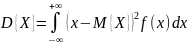
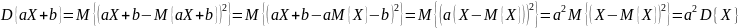 .
.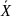 =(x1x2)
=(x1x2)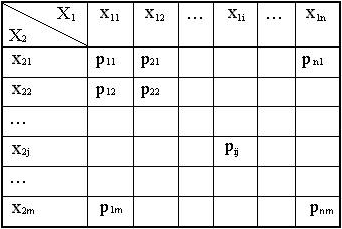
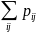 =1
=1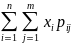 ;
;
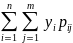 Эти формулы можно
записать в сокращенном виде.Обозначим
pi•=
Эти формулы можно
записать в сокращенном виде.Обозначим
pi•=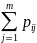 и
pj•=
и
pj•=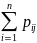 ,тогда
Mξ=
,тогда
Mξ=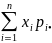 и
Mη=
и
Mη=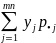
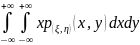 и Mη=
и Mη=
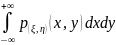 =pξ(x)
- плотность
распределения случайной величины ξ
, то Mξ=
=pξ(x)
- плотность
распределения случайной величины ξ
, то Mξ=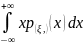 и Mη=
и Mη=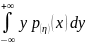
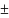 η)=D(ξ)+D(η)
η)=D(ξ)+D(η)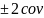 (ξ,η)
(ξ,η) =
=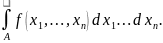 Функция
f(x1,…,xn)
называется плотностью распределения
случайного вектора. Она обладает след
свойствами:f(x1,…,xn)≥0
для
любого вектора(x1,…,xn)
Функция
f(x1,…,xn)
называется плотностью распределения
случайного вектора. Она обладает след
свойствами:f(x1,…,xn)≥0
для
любого вектора(x1,…,xn)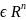 ;
; Эти
свойста берем из аксиом вероятности.(
Аксиома
1. Каждому случайному событию A
соответствует определенное число
Р(А), называемое его вероятностью и
удовлетворяющее условию 0≤ Р(А)≤1 .
Аксиома
2. Вероятность достоверного события
равна единице. Аксиома
3 (аксиома сложения вероятностей).
Пусть A и В — несовместные события.
Тогда вероятность того, что произойдет
хотя бы одно из этих двух событий,
равна сумме их вероятностей)Тогда
вектору с абсолютно непрерывным
распределением соответствует абсолютно
непрерывное вероятностное
пространство.Если случ вектор имеет
абсолютно непрерывное распределение
,то все его компоненты также имеют
абсолютно непрерывное распределения,причем
соответствующие плотности могут быть
записаны как функ одной переменной
,получющиеся интегрированием по
остальным переменным по пространству
Эти
свойста берем из аксиом вероятности.(
Аксиома
1. Каждому случайному событию A
соответствует определенное число
Р(А), называемое его вероятностью и
удовлетворяющее условию 0≤ Р(А)≤1 .
Аксиома
2. Вероятность достоверного события
равна единице. Аксиома
3 (аксиома сложения вероятностей).
Пусть A и В — несовместные события.
Тогда вероятность того, что произойдет
хотя бы одно из этих двух событий,
равна сумме их вероятностей)Тогда
вектору с абсолютно непрерывным
распределением соответствует абсолютно
непрерывное вероятностное
пространство.Если случ вектор имеет
абсолютно непрерывное распределение
,то все его компоненты также имеют
абсолютно непрерывное распределения,причем
соответствующие плотности могут быть
записаны как функ одной переменной
,получющиеся интегрированием по
остальным переменным по пространству
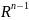 плотности распределения случ
вектора.Докажем этот факт для случ
n=2.Пусть
f(x1,x2)-плотность
распределения случ вектора (X1,X2)
и пусть [a,b)-произвольный
интервал.Тогда P(
плотности распределения случ
вектора.Докажем этот факт для случ
n=2.Пусть
f(x1,x2)-плотность
распределения случ вектора (X1,X2)
и пусть [a,b)-произвольный
интервал.Тогда P(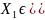 =P((X1,X2)
=P((X1,X2)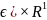 )=
)=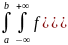 x1,x2)d
x1d
x2=
x1,x2)d
x1d
x2=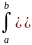 .
Если ввести функцию f1(x1)=
.
Если ввести функцию f1(x1)=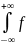 (x1,x2)dx2,то
для любого интервала [a,b)
P(X1
(x1,x2)dx2,то
для любого интервала [a,b)
P(X1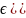 =
=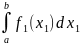 следовательно ,f1(x1)
является плотностью распределения
случайного вектора X1.Обратное
неверно:распределение случ вектора,сост
из компонент,имеющих абсолютно
непрерывное распределение,не только
не восстанавливается по распределениям
компонент,но даже может не быть
абсолютно непрерывным.(пример:случ
вектор сост из 2 тождественно равных
случ велечин)Если распределение
случайного вектора является абс
непрерывным ,то плотность есть смешанная
частная производная функции распределения
по всем переменным :
f(x1,…,xn)=
следовательно ,f1(x1)
является плотностью распределения
случайного вектора X1.Обратное
неверно:распределение случ вектора,сост
из компонент,имеющих абсолютно
непрерывное распределение,не только
не восстанавливается по распределениям
компонент,но даже может не быть
абсолютно непрерывным.(пример:случ
вектор сост из 2 тождественно равных
случ велечин)Если распределение
случайного вектора является абс
непрерывным ,то плотность есть смешанная
частная производная функции распределения
по всем переменным :
f(x1,…,xn)=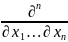 F(x1,…,xn).Математическое
ожидание:M{g(X1,…,Xn)}=
F(x1,…,xn).Математическое
ожидание:M{g(X1,…,Xn)}=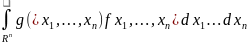 ,где
f(x1,…,xn)
– плотность распр случ вектора.
,где
f(x1,…,xn)
– плотность распр случ вектора.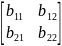 =cov(x)=M{(x-M(x))(x-M(x))}
cov(x)=
=cov(x)=M{(x-M(x))(x-M(x))}
cov(x)= *(x1i-m1,x2j-x2)P(x1=x1i,x2=x2j)
cov(x)=
*(x1i-m1,x2j-x2)P(x1=x1i,x2=x2j)
cov(x)=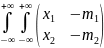 *(x1-m1,x2-m2)f(x1,x2)dx1dx2
b11=
*(x1-m1,x2-m2)f(x1,x2)dx1dx2
b11=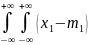 2f(x1,x2)dx1dx2=
2f(x1,x2)dx1dx2=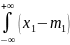 2
2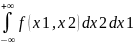 =D(x1)⤇b22=D(x2)
b12=b21⤇b12=
=D(x1)⤇b22=D(x2)
b12=b21⤇b12=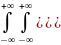 x1-m1)(
x2-m2)f(x1,x2)dx1dx2=cov(X1,X2)
x1-m1)(
x2-m2)f(x1,x2)dx1dx2=cov(X1,X2)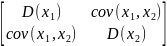
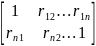 rij=
rij= – коэф корреляции
– коэф корреляции
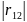 ≤1
Док-во:
≤1
Док-во:
 (α(x1-m1)-(x2-m2))2≥0;
α2(x1-m1)=2α(x1-m1)(x2-m2)+(x2-m2)≥0;
α2
x1-m1)2f(x1,x2)dx1dx2-2α
x1-mi)
;(x2-m2)
f(x1,x2)
dx1dx2+
x2-m2)2f
(x1,x2)dx1dx2=
α2
(α(x1-m1)-(x2-m2))2≥0;
α2(x1-m1)=2α(x1-m1)(x2-m2)+(x2-m2)≥0;
α2
x1-m1)2f(x1,x2)dx1dx2-2α
x1-mi)
;(x2-m2)
f(x1,x2)
dx1dx2+
x2-m2)2f
(x1,x2)dx1dx2=
α2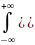 x1-m1)2f(x1)dx1-2αcov(x1,x2)+
x2-m2)2f(x2)dx2=
α2D(x1)-2αcov(x1,x2)+D(x2)≥0
x1-m1)2f(x1)dx1-2αcov(x1,x2)+
x2-m2)2f(x2)dx2=
α2D(x1)-2αcov(x1,x2)+D(x2)≥0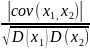 ≤1⤇
≤1⤇-1≤r12≤1
ч.т.д
≤1⤇
≤1⤇-1≤r12≤1
ч.т.д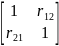
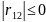 ,25-можно
пренебречь ,0,25
,25-можно
пренебречь ,0,25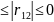 ,75-нельзя,
,75-нельзя,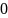 ,75
,75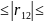 1-второй
нет(или можно высчитать через 1)
1-второй
нет(или можно высчитать через 1)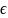 A1}
и {X2
A2},где
A1
и A2-произвольные
борелевские множества на прямой.
Независимость событий означает
A1}
и {X2
A2},где
A1
и A2-произвольные
борелевские множества на прямой.
Независимость событий означает
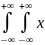 1x2f(x1,x2)dx1dx2=
1x2f(x1,x2)dx1dx2=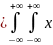 1x2f(x1)f(x2)dx1dx2
1x2f(x1)f(x2)dx1dx2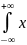 1f(x1)dx1
2f(x2)dx2=M{X1}M{X2}
1f(x1)dx1
2f(x2)dx2=M{X1}M{X2} 2→
.
Требуется найти функцию (а если
существует, то и плотность) распределения
случайной величины η=g(ξ1,ξ2)
.
2→
.
Требуется найти функцию (а если
существует, то и плотность) распределения
случайной величины η=g(ξ1,ξ2)
.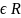 ,и
область Dx
,и
область Dx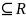 2
состоит
из точек (x1,x2)
таких ,что g(x1,x2)<x.Тогда
случайная величина η= g(ξ1,ξ2)
имеет функцию распределения
2
состоит
из точек (x1,x2)
таких ,что g(x1,x2)<x.Тогда
случайная величина η= g(ξ1,ξ2)
имеет функцию распределения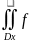 ξ1,
ξ2(x1,x2)dx1dx2.
ξ1,
ξ2(x1,x2)dx1dx2.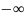 до
до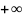 , и внутреннего — по переменной x2
, которая при каждом x1
должна быть меньше, чем x-x1
. Здесь Dx={(x1,x2)|x1
,
x2
(
,x-x1)
}. Поэтому
, и внутреннего — по переменной x2
, которая при каждом x1
должна быть меньше, чем x-x1
. Здесь Dx={(x1,x2)|x1
,
x2
(
,x-x1)
}. Поэтому ξ1+ξ2(t)dt,
где
ξ1+ξ2(t)dt,
где