9091_Клименко_вар_25
.docxКонтрольная работа
по дисциплине «Теория вероятности и математическая статистика» ВАРИАНТ № 25
Студент гр. 9091 Клименко Н.Ю
|
Вариант 25 |
1 |
Пусть
0, 1, 4, 3, 4, 3, 4, 3,4,4 –выборка из совокупности
с теоретическим биномиальным
распределением :
k=0,..., 4. Построить оценку максимального правдоподобия для параметра p |
2 |
Студент ознакомился только с половиной экзаменационных вопросов. Если он получает билет, с которым он ознакомился, то вероятность сдать экзамен равна ½, в противном случае эта вероятность равна нулю. Определить вероятность сдачи экзамена. |
3 |
При
обработке выборки объема
16
получили доверительный интервал для математического ожидания доверительной вероятности 0.9. |
4 |
При выстреле по мишени стрелок попадает в десятку с вероятностью 0.5, в девятку - 0.3, в восьмерку – 0.1, в семерку – 0.05, в шестерку – 0.05. Стрелок сделал 100 выстрелов. Вычислить математическое ожидание числа набранных очков. |
Ответы: 1. 3/4
2. 1/4
3. (17.4170; 22.5830)
4. 915
Задача 1.
Запишем логарифм функции максимального правдоподобия
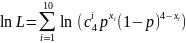
Продифференцируем L по p и приравняем 0:
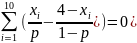
Это можно привести к виду
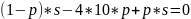
Где
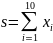
Отсюда
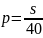
Вычислим s

Получаем оценку для p
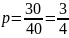

Ответ:
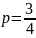
Задача 2.
Введем обозначения:
Событие А – студенту достался билет, который он учил;
Событие Б - студенту достался билет, который он не учил.
Так
как студент знает ровно половину билетов,
то вероятность наступления события А
равна р(А)=
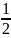 ,
и вероятность наступления события Б:
р(Б) =
,
и вероятность наступления события Б:
р(Б) =
Событие С – студент сдал экзамен.
Вероятность наступления события С при условии наступления события А равна , т.е.
р(С/А) = .
Вероятность наступления события С при условии наступления события Б равна 0, т.е.
р(С/Б) = 0.
По теореме условной вероятности найдем вероятность сдачи экзамена – р(С):
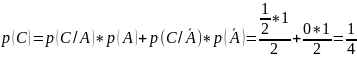
Ответ:
вероятность сдать экзамен равна
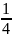 .
.
Задача 3.
Доверительный
интервал для нормально распределенной
случайной величины с неизвестным
квадратичным распределением
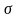 ,
но с известным исправленным средним
квадратичным отклонением s,
выборочным средним, объемом выборки n
и доверительной вероятностью
,
но с известным исправленным средним
квадратичным отклонением s,
выборочным средним, объемом выборки n
и доверительной вероятностью
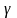 ,
имеет вид:
,
имеет вид:
(
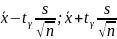 )
)
Где
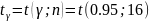 -
находим по таблице значений коэффициента
Стьюдента.
-
находим по таблице значений коэффициента
Стьюдента.
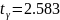 0
0
Получаем доверительный интервал:
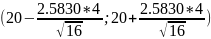 ,
,
если упростить, то получим доверительный интервал:
(17.4170; 22.5830)
Ответ: доверительный интервал (17.4170; 22.5830)
Задача 4.
Составим закон распределения числа попаданий:
|
1 |
2 |
3 |
4 |
5 |
Количество очко при одном попадании, ki |
10 |
9 |
8 |
7 |
6 |
Вероятность попадания, pi |
0,5 |
0,3 |
0,1 |
0,05 |
0,05 |
Число попаданий, Хi = n*pi |
100*0,5=50 |
100*0,3=30 |
100*0,1=10 |
100*0,05=5 |
100*0,05=5 |
Математическое ожидание числа набранных очков:
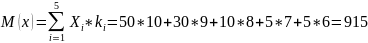
Ответ: математическое ожидание числа набранных очков равно 915.

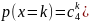
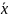
20, s
4.
Построить
20, s
4.
Построить